A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN
Abstract
:1. Introduction
2. MTF Theory
2.1. State Transition Probability Matrix
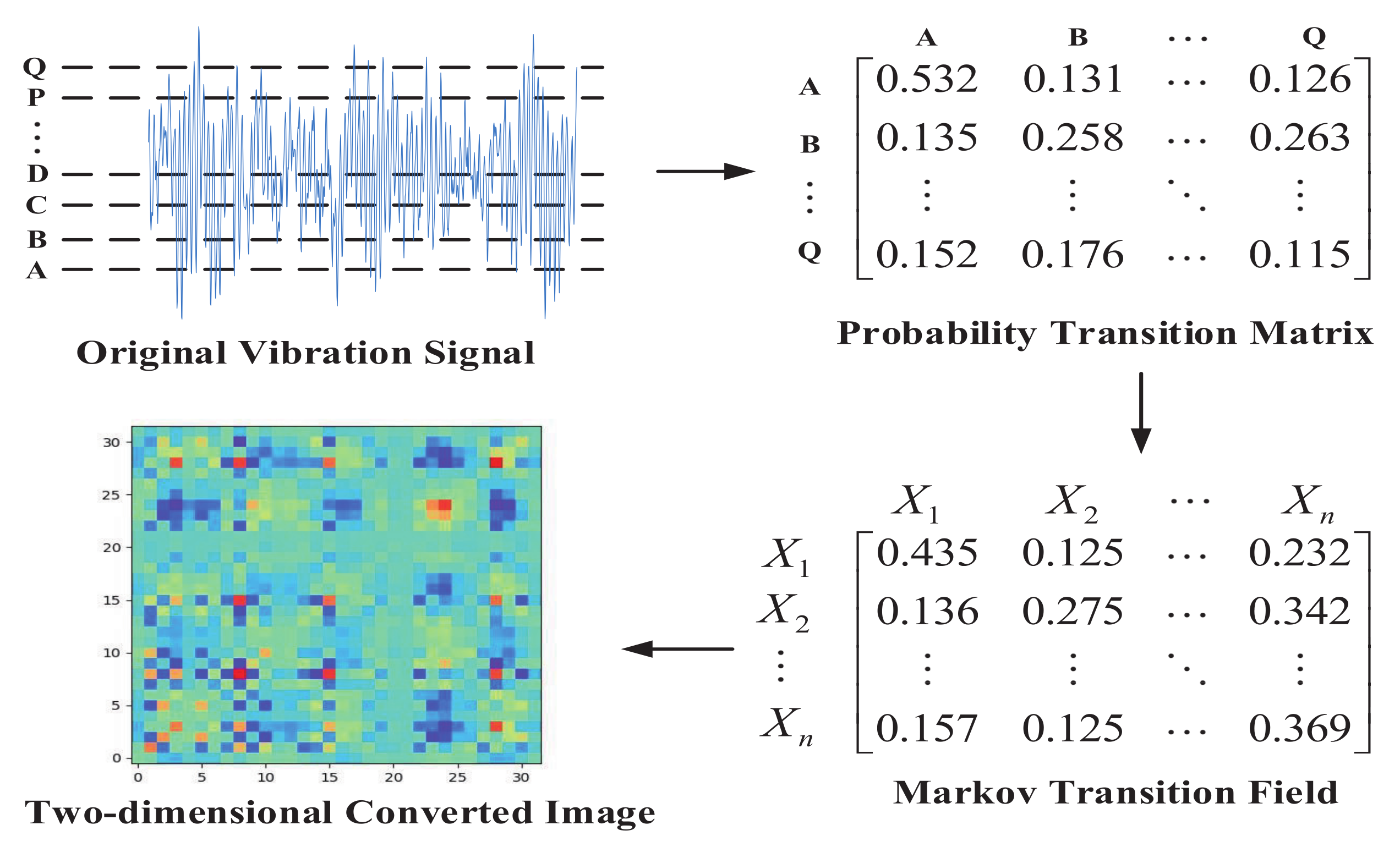
2.2. Markov Transformation Process
- Divide the vibration signal into Q parts.
- Obtain the probability conversion matrix of size.
- Convert the probability matrix to MTF.
- Transform MTF into a 2-D image.
3. The Brief Introduction of CNN
3.1. Convolutional Layer
3.2. Pooling Layer
3.3. Fully Connected Layer
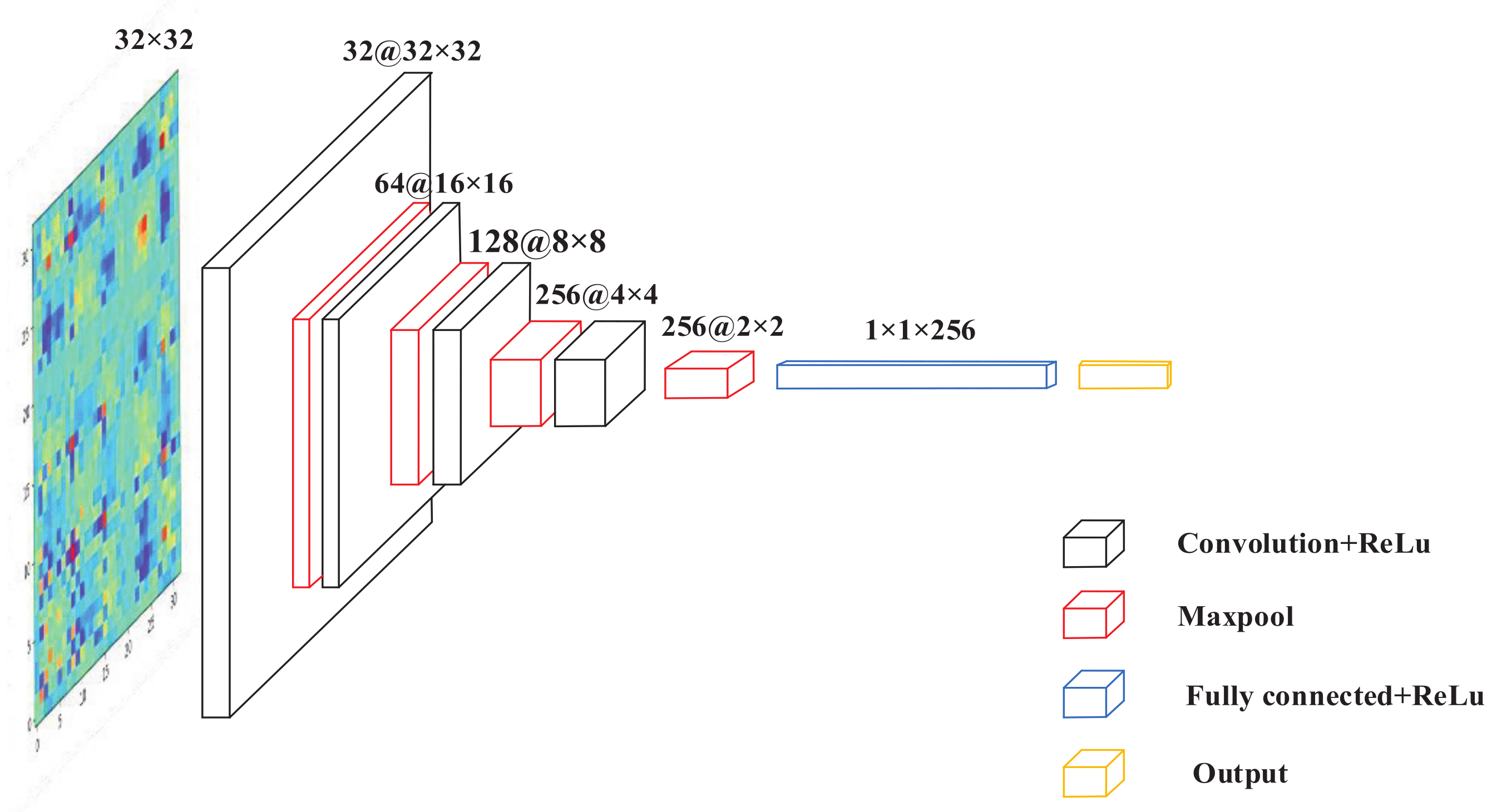
3.4. Proposed CNN Structure
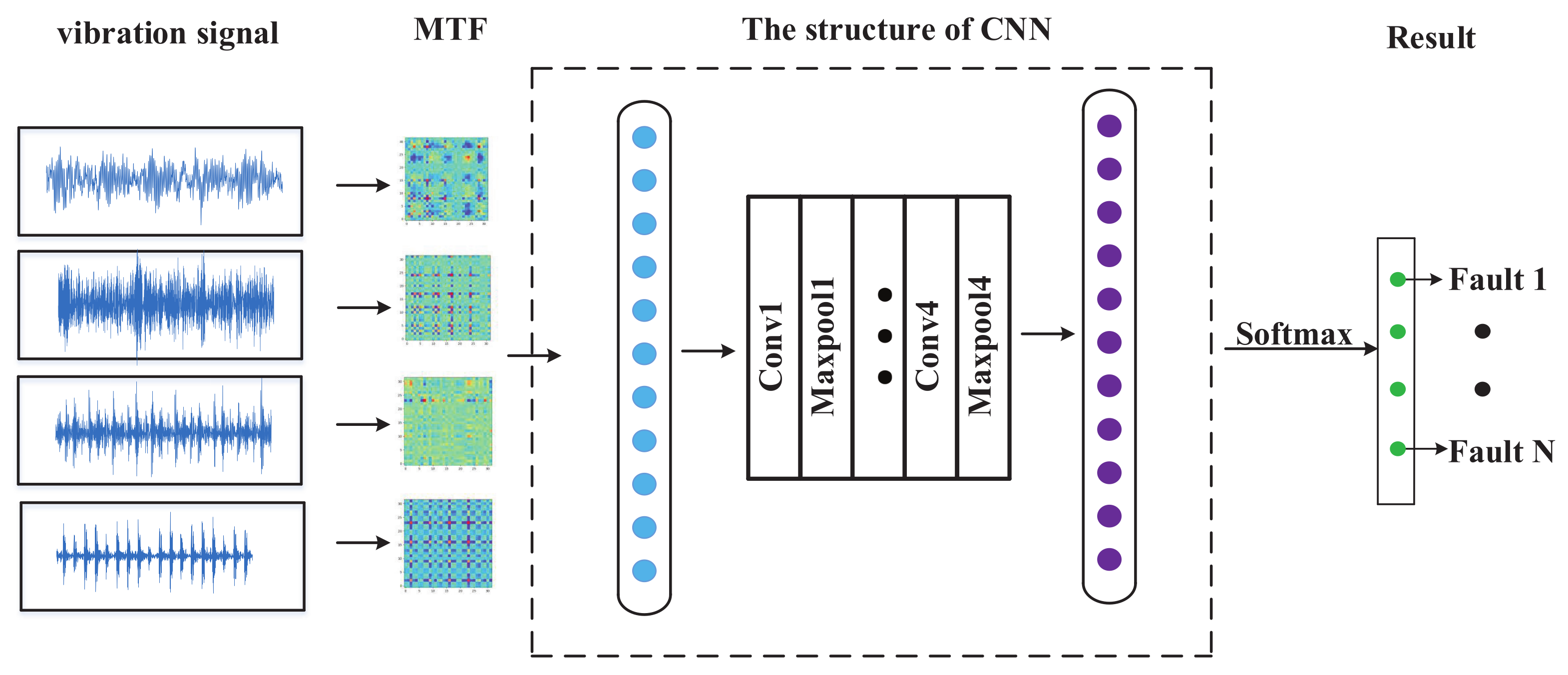
4. The Process of MTF-CNN
- Collect the vibration signals.
- Convert 1-D vibration signals into MTF images.
- Input the images into CNN for classification.
- Obtain the result of fault classification.
5. Experiment Test
5.1. Experiment 1
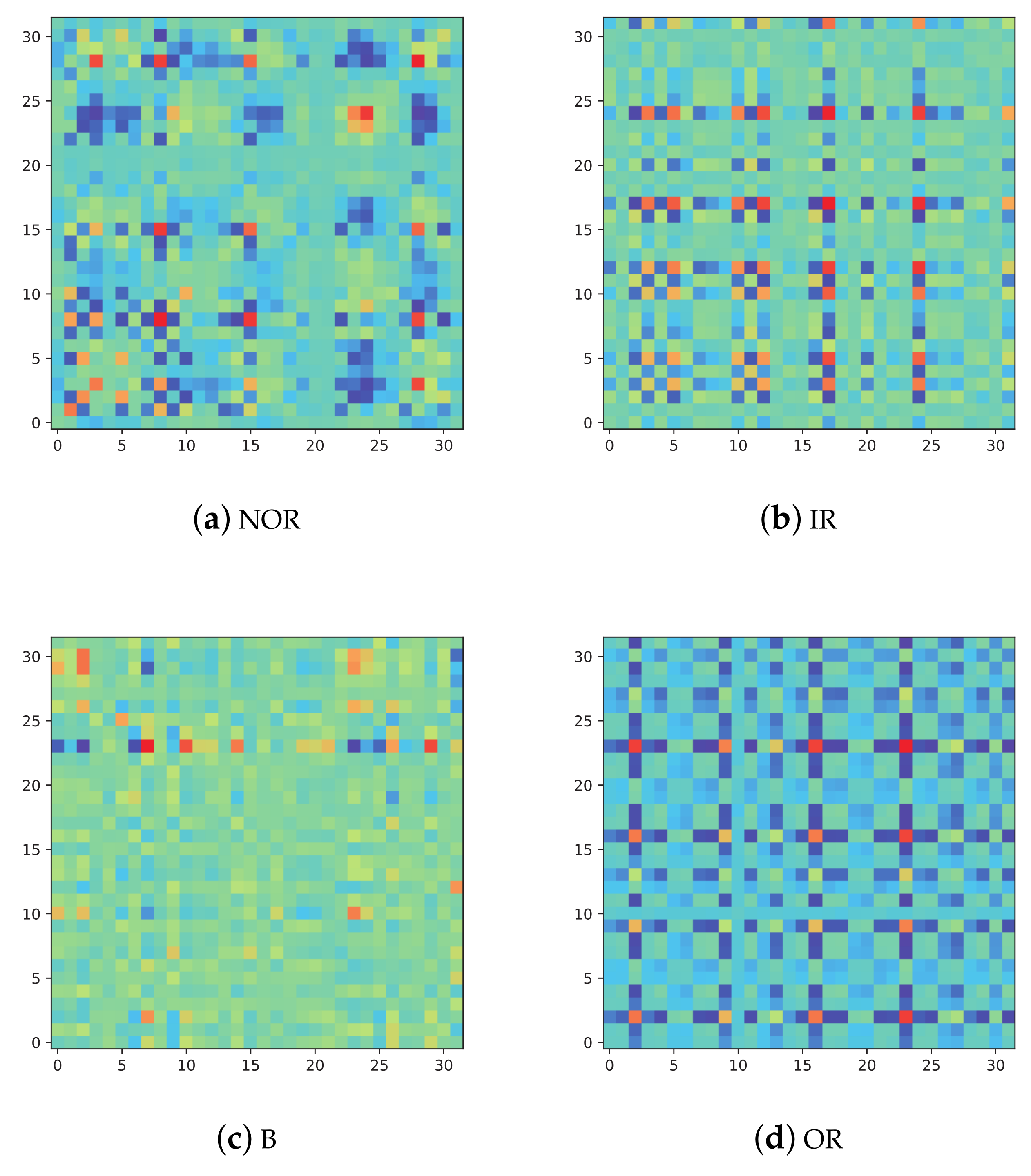
5.1.1. Data Description
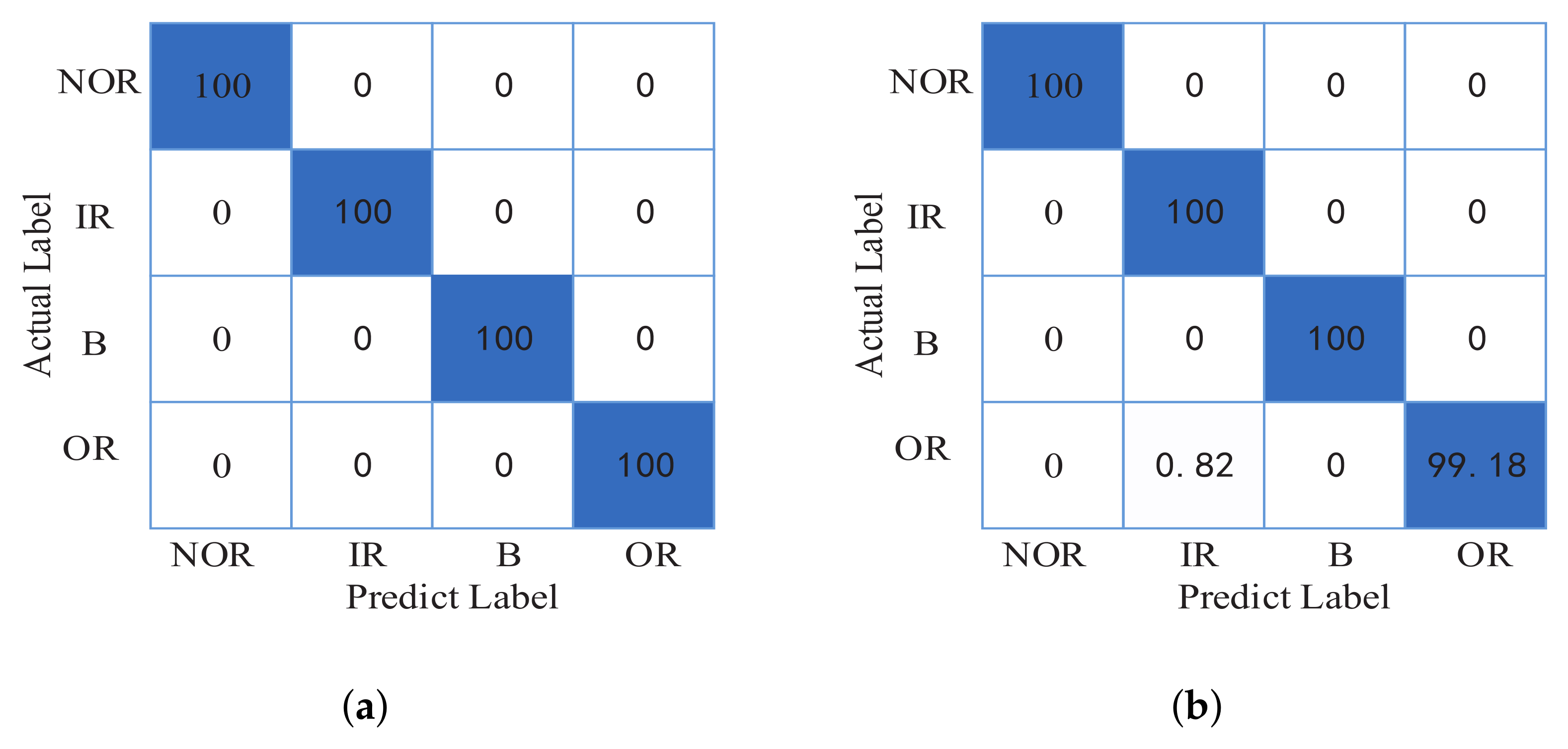
5.1.2. Result Analysis
5.2. Experiment 2
5.2.1. Data Description
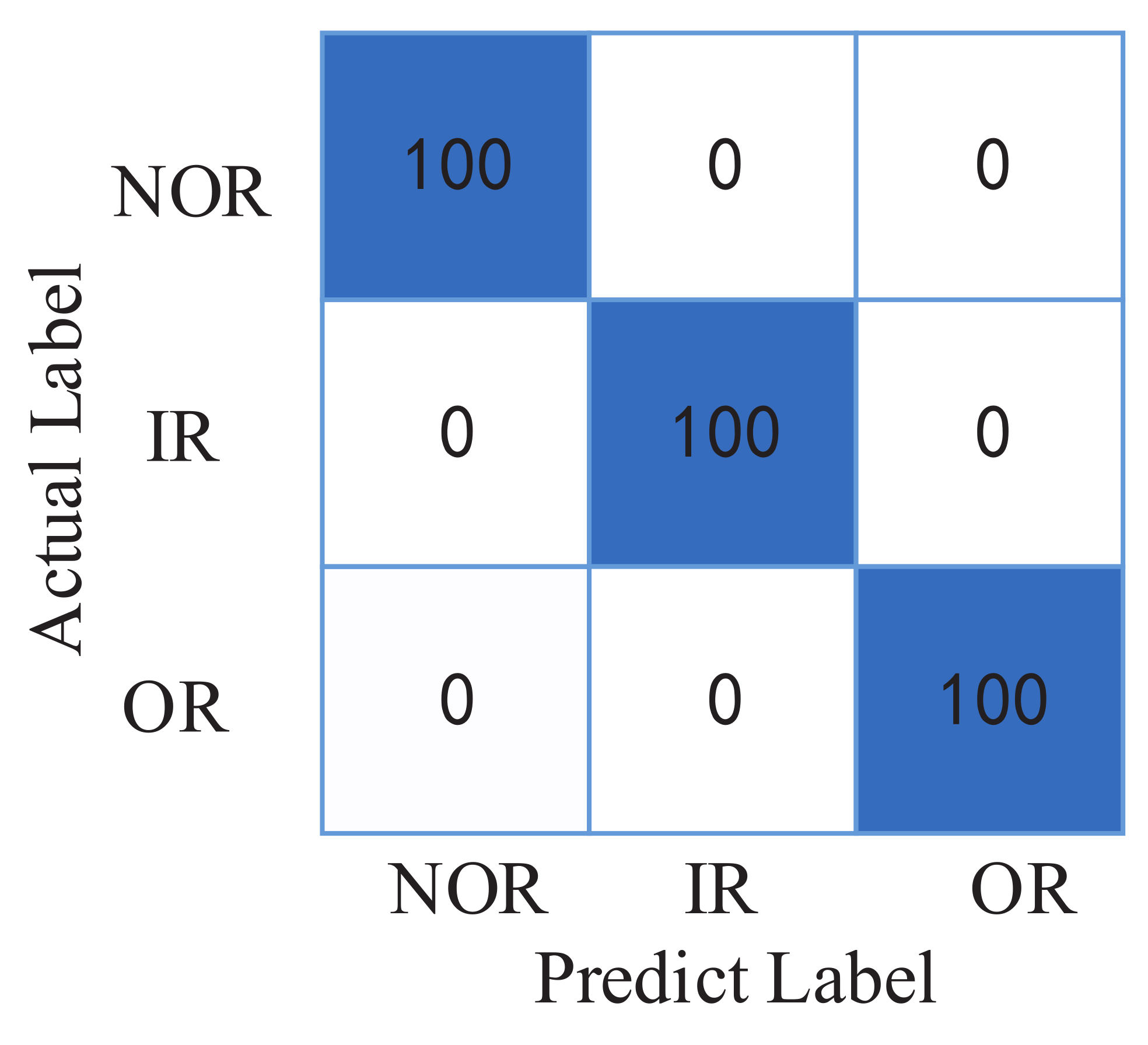
5.2.2. Result Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heng, A.; Zhang, S.; Tan, A.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Proc. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Zhao, H. An enhancement deep feature fusion method for rotating machinery fault diagnosis. Knowl.-Based Syst. 2017, 119, 200–220. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mech. Syst. Signal Proc. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- Xu, M.; Feng, G.; He, Q.; Gu, F.; Ball, A. Vibration characteristics of rolling element bearings with different radial clearances for condition monitoring of wind turbine. Appl. Sci. 2020, 14, 4731. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Dybała, J.; Zimroz, R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Ying, Y.; Li, J.; Chen, Z.; Guo, J. Study on rolling bearing on-line reliability analysis based on vibration information processing. Comput. Electr. Eng. 2018, 69, 842–851. [Google Scholar] [CrossRef]
- Wang, J.; Peng, Y.; Qiao, W. Current-aided order tracking of vibration signals for bearing fault diagnosis of direct-drive wind turbines. IEEE Trans. Ind. Electron. 2016, 63, 6336–6346. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J.; Lei, Y. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Proc. 2017, 92, 173–195. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y.; Cao, Z. Optimal demodulation subband selection for sun gear crack fault diagnosis in planetary gearbox. Measurement 2018, 125, 554–563. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Proc. 2017, 93, 460–493. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liang, X.; Xu, M.; Huang, W. Early fault feature extraction of rolling bearing based on ICD and tunable Q-factor wavelet transform. Mech. Syst. Signal Proc. 2017, 86, 204–223. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Wang, X.; Wu, J.; Li, Z. An improved local mean decomposition method based on improved composite interpolation envelope and its application in bearing fault feature extraction. ISA Trans. 2020, 97, 365–383. [Google Scholar] [CrossRef] [PubMed]
- Riaz, F.; Hassan, A.; Rehman, S.; Niazi, I.; Dremstrup, K. EMD-based temporal and spectral features for the classification of EEG signals using supervised learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 28–35. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Proc. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Quiroz, J.; Mariun, N.; Mehrjou, M.; Izadi, M.; Misron, N.; Radzi, M. Fault detection of broken rotor bar in LS-PMSM using random forests. Measurement 2018, 116, 273–280. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal Proc. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient kNN classification with different numbers of nearest neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Proc. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M.; Zhao, Z. A novel intelligent detection method for rolling bearing based on IVMD and instantaneous energy distribution-permutation entropy. Measurement 2018, 130, 435–447. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, H.; Jiang, H.; Zhang, H.; Duan, W.; Liang, T.; Wu, S. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing. Mech. Syst. Signal Proc. 2018, 100, 743–765. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Proc. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst. Man Cybern. -Syst. 2017, 49, 136–144. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; De, S.C. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE-ASME Trans. Mechatron. 2017, 23, 101–110. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Qin, Y. Understanding and learning discriminant features based on multiattention 1DCNN for wheelset bearing fault diagnosis. IEEE Trans. Ind. Inform. 2019, 16, 5735–5745. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Smith, A.; Robert, B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Proc. 2015, 64, 100–131. [Google Scholar] [CrossRef]




| Layer | CNN Models | Kernel Size | Padding | Stride |
|---|---|---|---|---|
| Conv | 1 | 1 | ||
| Maxpool | No | 1 | ||
| Conv | 1 | 1 | ||
| Maxpool | No | 1 | ||
| Conv | 1 | 1 | ||
| Maxpool | No | 1 | ||
| Conv | 1 | 1 | ||
| Maxpool | No | 1 | ||
| FCl | 256 | - | - |
| Method | Highest Accuracy | Lowest Accuracy | Mean |
|---|---|---|---|
| MTF-CNN | |||
| LSTM | |||
| FE-LSTM | |||
| SVM | |||
| FE-SVM |
| Method | Highest Accuracy | Lowest Accuracy | Mean |
|---|---|---|---|
| MTF-CNN | |||
| LSTM | |||
| FE-LSTM | |||
| SVM | |||
| FE-SVM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wang, W.; Zhang, X.; Iu, H.H.-C. A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN. Entropy 2022, 24, 751. https://doi.org/10.3390/e24060751
Wang M, Wang W, Zhang X, Iu HH-C. A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN. Entropy. 2022; 24(6):751. https://doi.org/10.3390/e24060751
Chicago/Turabian StyleWang, Mengjiao, Wenjie Wang, Xinan Zhang, and Herbert Ho-Ching Iu. 2022. "A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN" Entropy 24, no. 6: 751. https://doi.org/10.3390/e24060751
APA StyleWang, M., Wang, W., Zhang, X., & Iu, H. H.-C. (2022). A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN. Entropy, 24(6), 751. https://doi.org/10.3390/e24060751







