Information Hiding Based on Statistical Features of Self-Organizing Patterns
Abstract
:1. Introduction
2. Preliminaries
2.1. Beddington-DeAngelis-Type Predator-Prey Model with Self- and Cross-Diffusion
2.2. The Numerical Model and Types of Self-Organizing Patterns
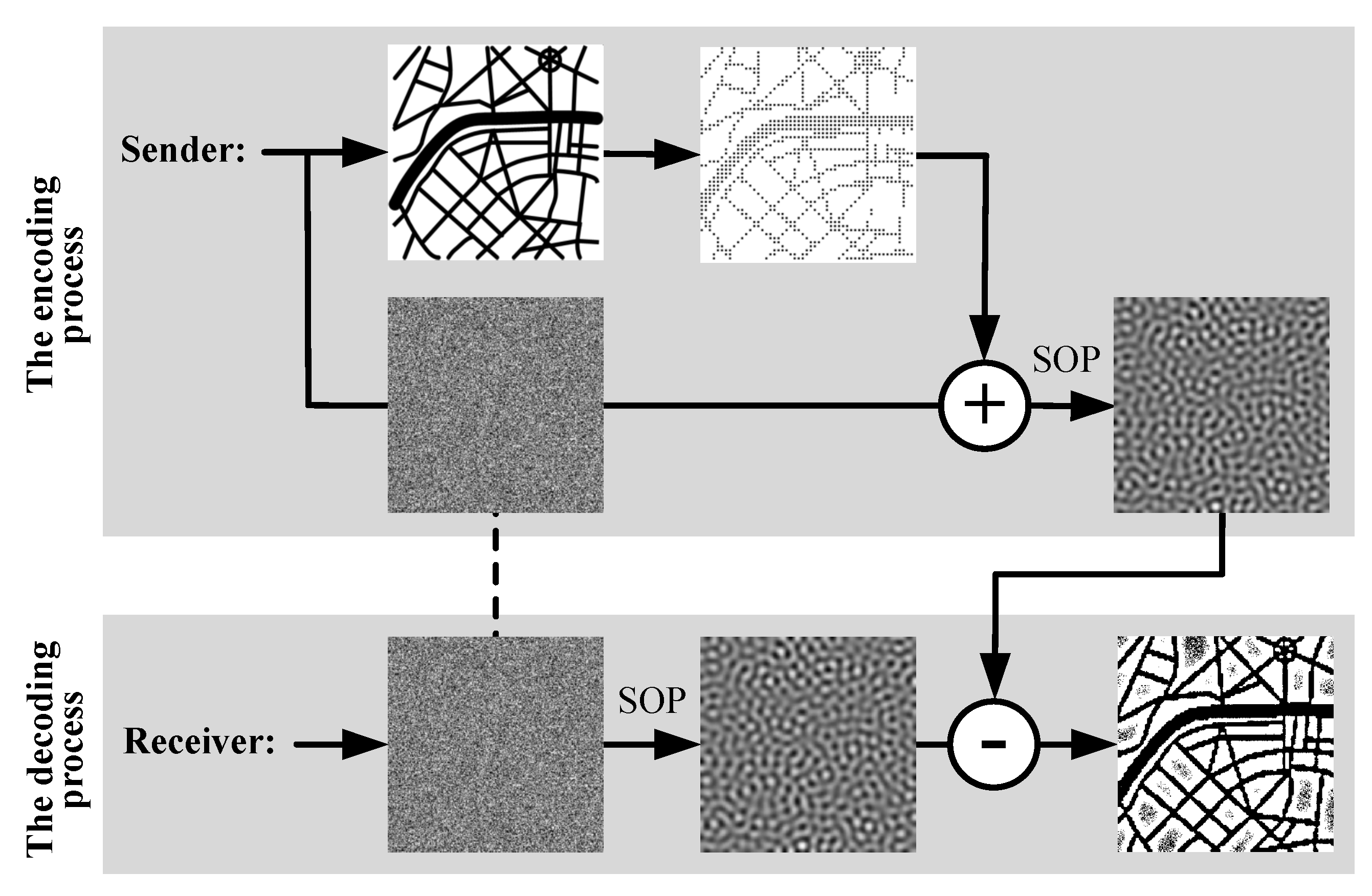
2.3. A Secure Communication System Based on Self-Organizing Patterns
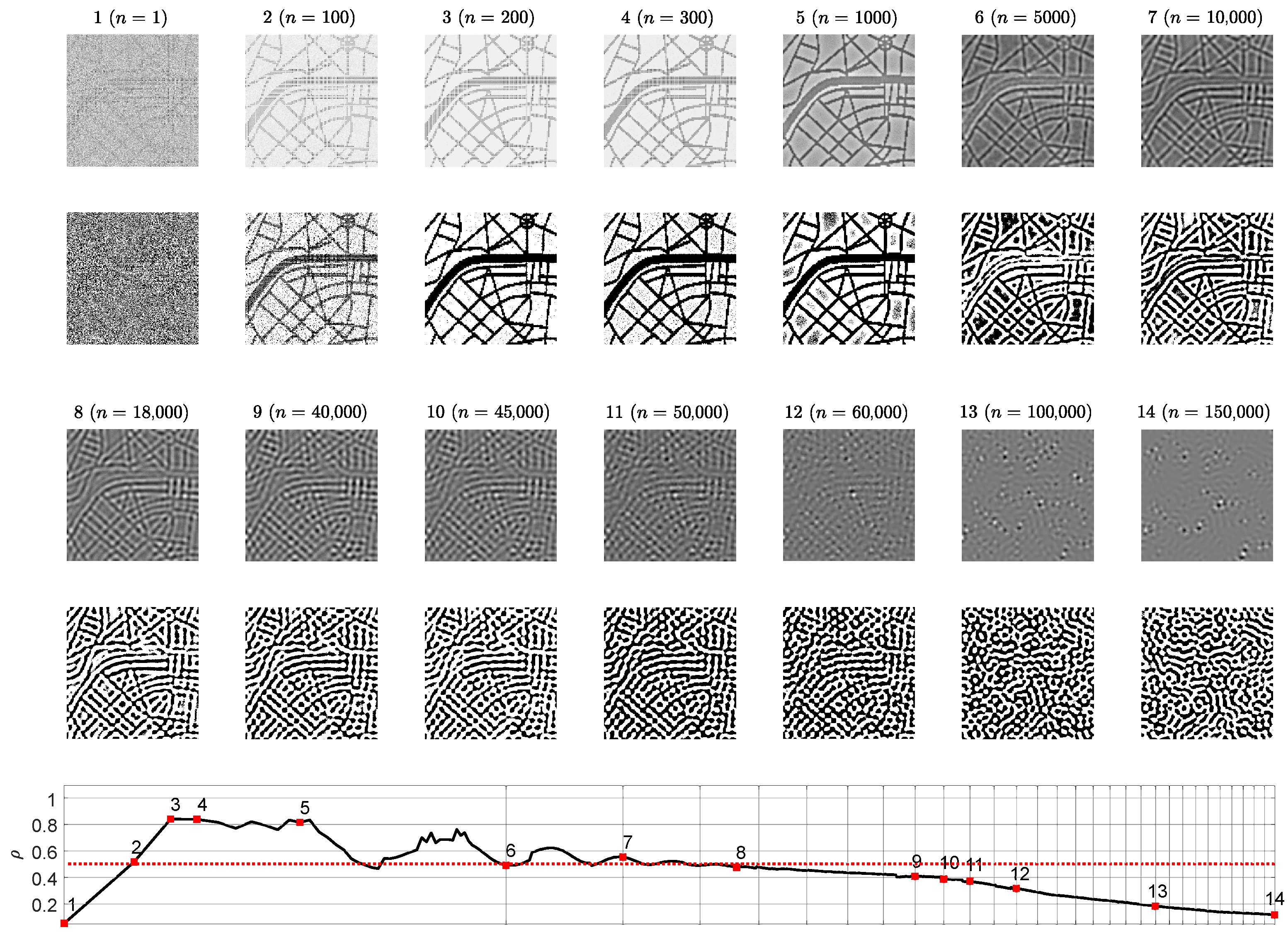
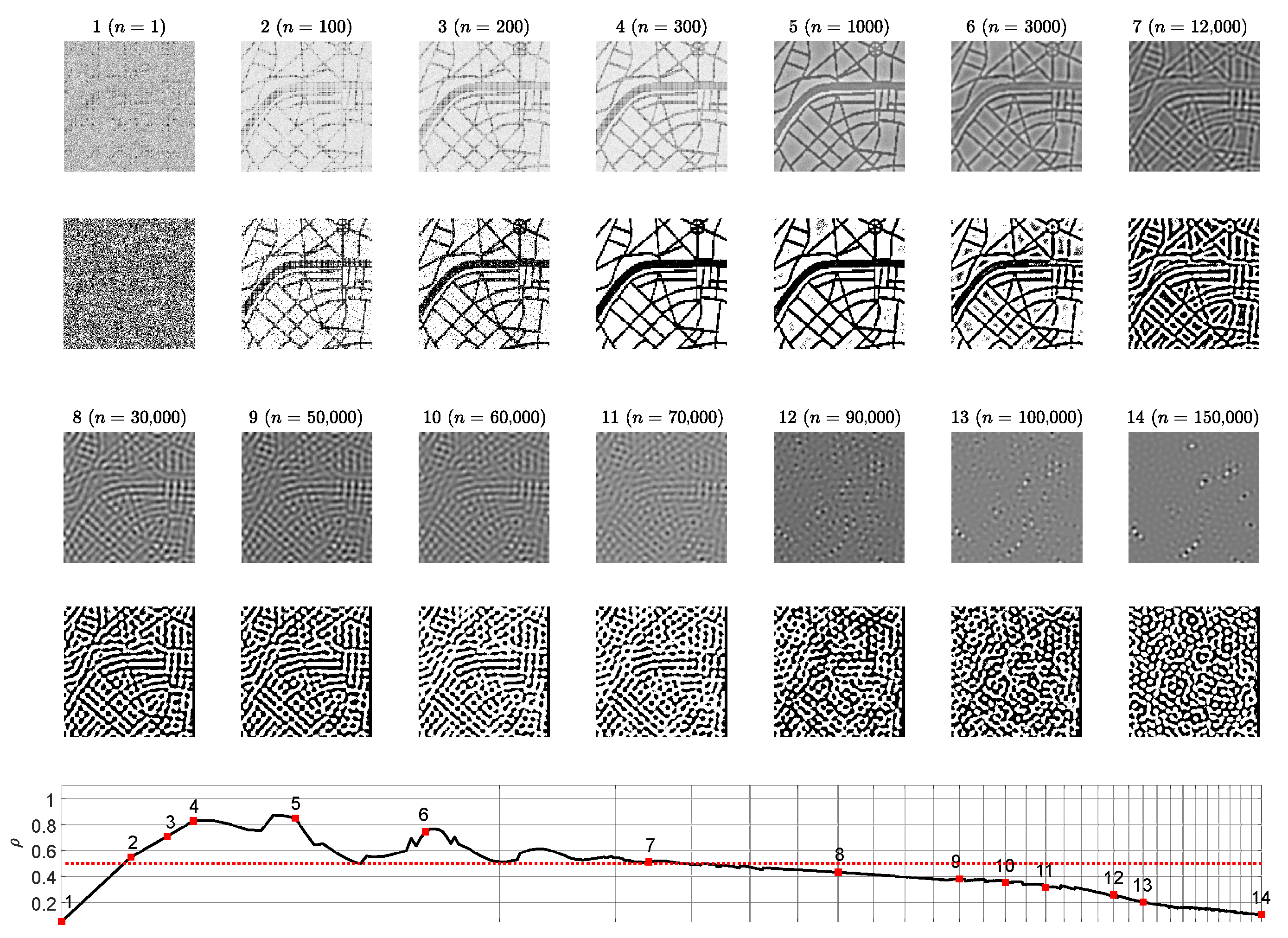
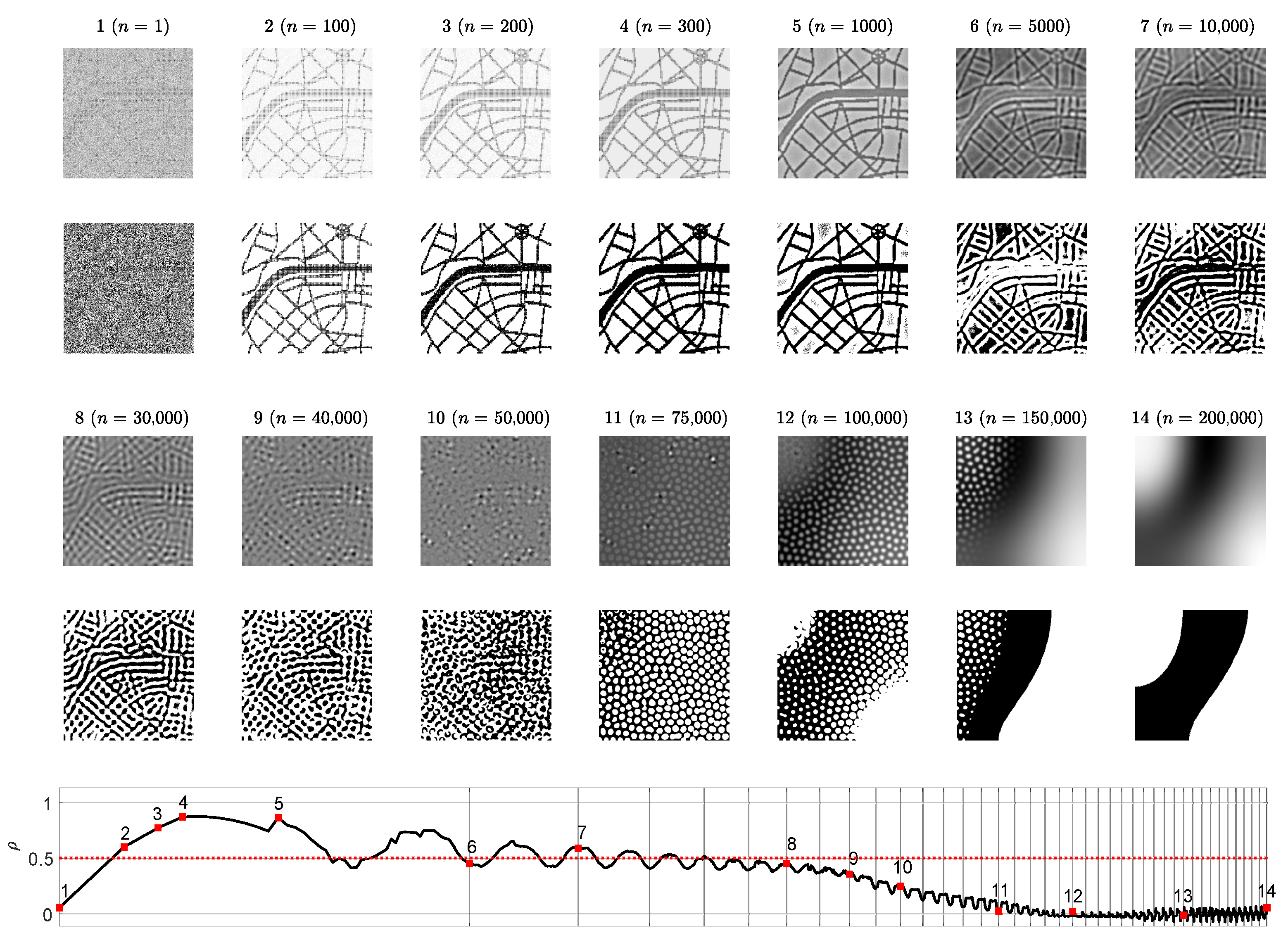
2.4. The Wada Index for the Evaluation of the Image Complexity
- s—the size of the border of a square observation window measured in the number of pixels; .
- m—the number of different colors in the observation window; .
- , —the number of the k-th color pixels in the observation window.
- , —the discrete probability of the k-th color in the observation window.
- The indicator function is equal to 1 if the number of colors in the observation window is greater or equal than 2:
- The indicator function is equal to 1 if the number of colors in the observation window is greater or equal than 3:
- The Shannon entropy of different colors in the observation window:
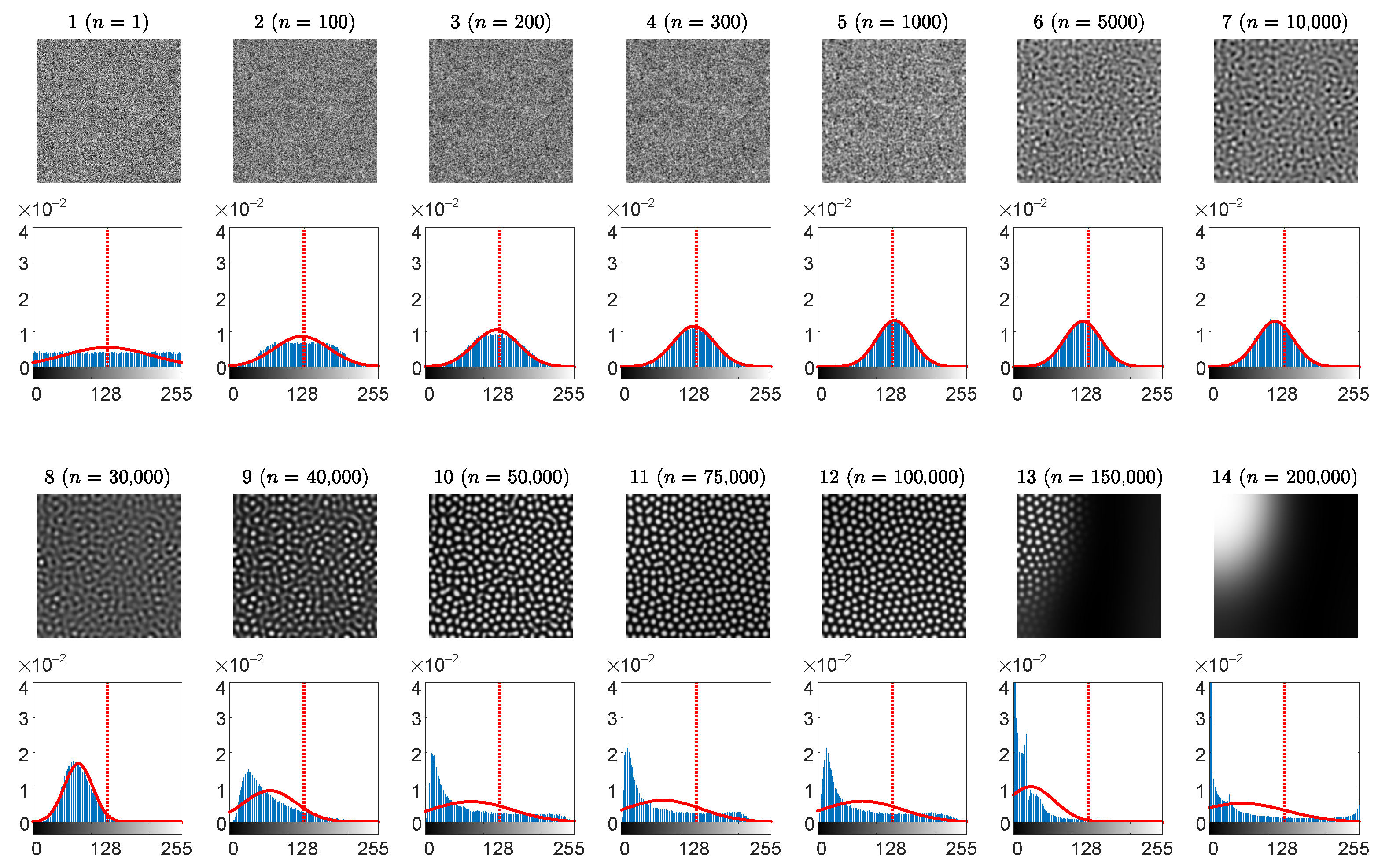
2.5. Other Statistical Indicators for the Evaluation of the Image Complexity
3. Results and Discussion
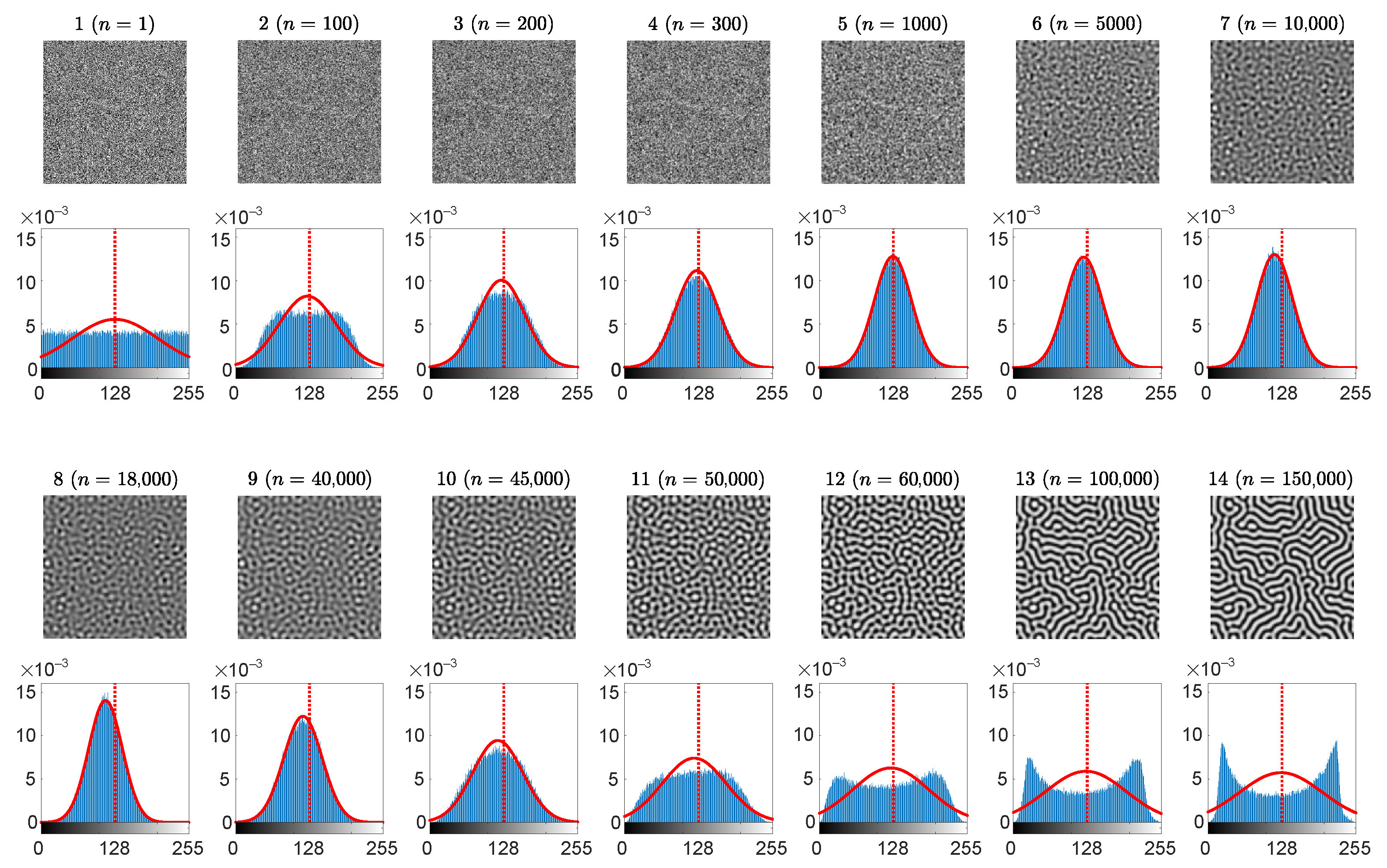
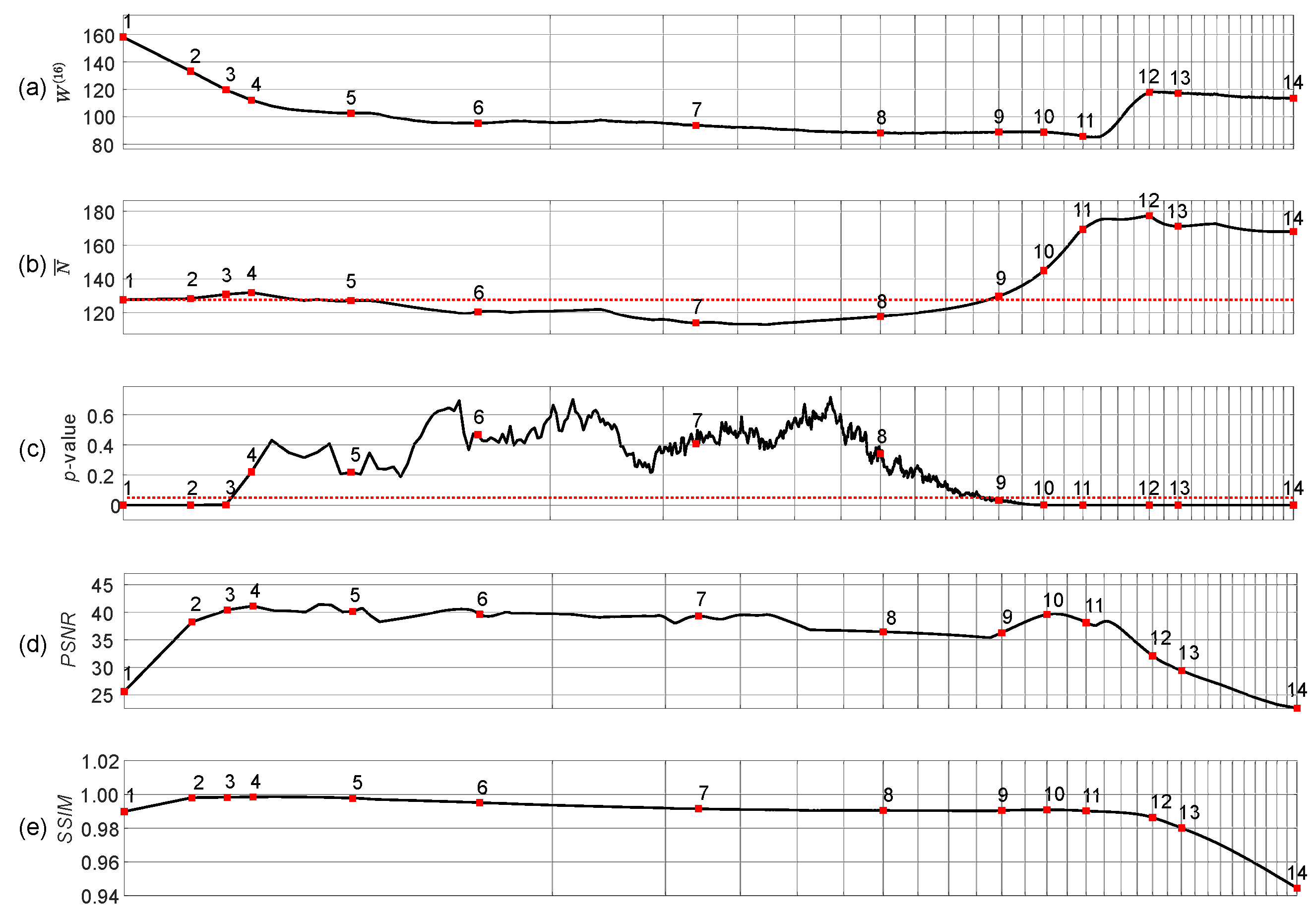
3.1. Optimal Information Hiding in Stripe-Type Patterns
- The Wada index should drop down from the initial value and should get stabilized before growing back again.
- The mean of the brightness of the pattern should remain around the average between black and white before dropping down significantly below the average.
- The p-value of the Kolmogorov-Smirnov criterion should grow above what indicates that the distribution becomes Gaussian.
3.2. Optimal Information Hiding in Patterns of Spots
3.3. Optimal Information Hiding in Unstable Patterns
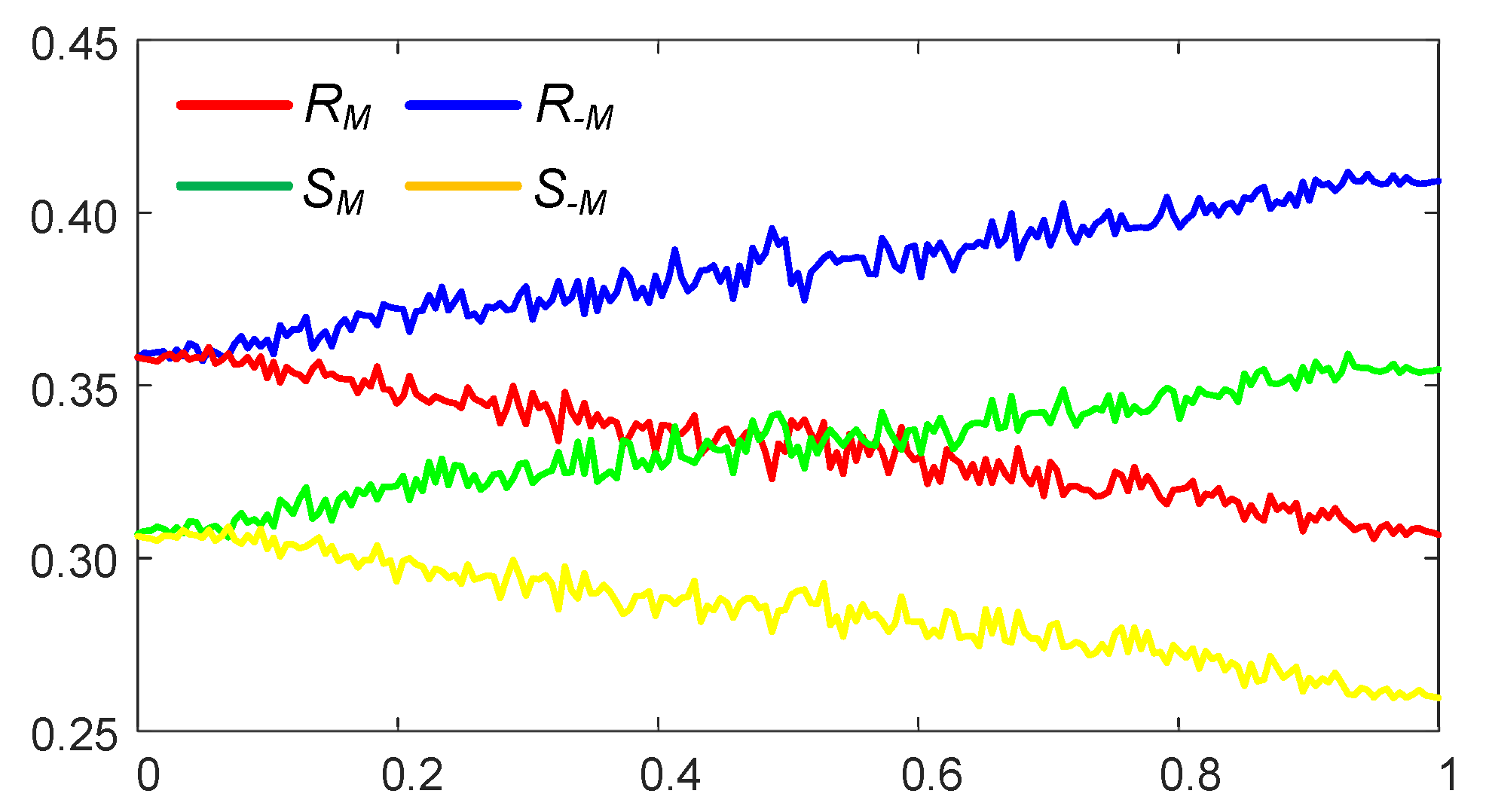
3.4. The Robustness of the Proposed Scheme
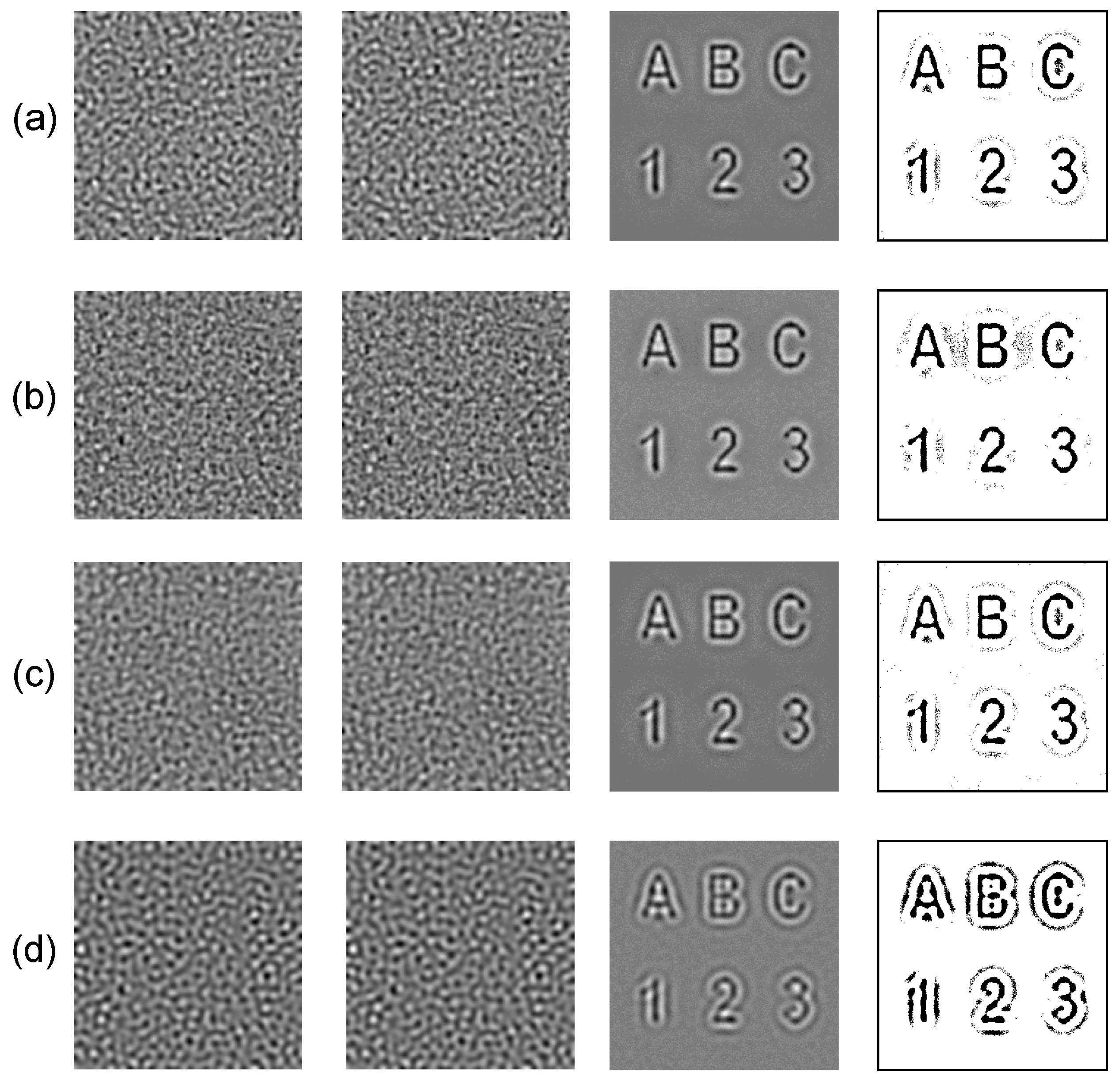
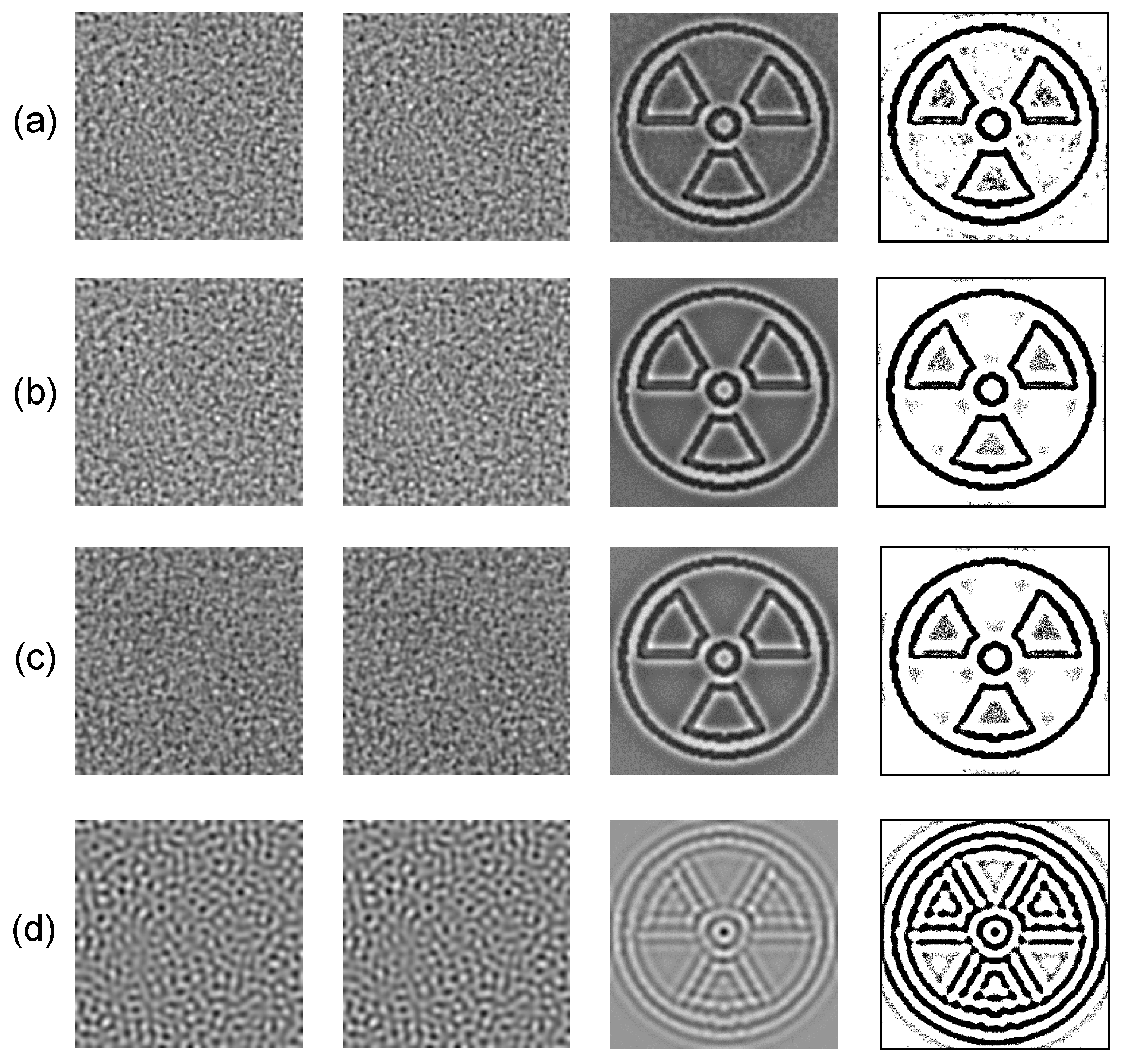
3.5. More Examples of Different Carrier Patterns and Hidden Images
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kessler, G.C.; Hosmer, C. Chapter 2—An Overview of Steganography. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 2011; Volume 83, pp. 51–107. [Google Scholar] [CrossRef]
- Rafat, K.F. Prudently Secure Information Theoretic LSB Steganography for Digital Grayscale Images. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 594–614. [Google Scholar] [CrossRef]
- Durdu, A. A new reversible low-distortion steganography method that hides images into RGB images with low loss. Multimed. Tools Appl. 2022, 81, 953–973. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, D.K. Steganography Using Block Pattern Detection in AMBTC Image. In Advances in Smart Communication and Imaging Systems; Agrawal, R., Kishore Singh, C., Goyal, A., Eds.; Springer: Singapore, 2021; pp. 723–734. [Google Scholar]
- Kim, H.Y.; Mayer, J. Data Hiding for Binary Documents Robust to Print-Scan, Photocopy and Geometric Distortions. In Proceedings of the Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI 2007), Belo Horizonte, Brazil, 7–10 October 2007; pp. 105–112. [Google Scholar] [CrossRef]
- Jiao, S.; Feng, J. Image steganography with visual illusion. Opt. Express 2021, 29, 14282–14292. [Google Scholar] [CrossRef] [PubMed]
- Abed, S.; Al-Roomi, S.A.; Al-Shayeji, M. Efficient Cover Image Selection Based on Spatial Block Analysis and DCT Embedding. J. Image Video Process. 2019, 2019. [Google Scholar] [CrossRef]
- Sneyd, J.; Theraula, G.; Bonabeau, E.; Deneubourg, J.L.; Franks, N.R. Chapter 1—What is self-organization? In Self-Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2020; pp. 7–14. [Google Scholar] [CrossRef]
- Siebert, B.A.; Hall, C.L.; Gleeson, J.P.; Asllani, M. Role of modularity in self-organization dynamics in biological networks. Phys. Rev. E 2020, 102, 052306. [Google Scholar] [CrossRef]
- Curantz, C.; Manceau, M. Trends and variation in vertebrate patterns as outcomes of self-organization. Curr. Opin. Genet. Dev. 2021, 69, 147–153. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, T.; Dai, L.; Pan, G.; Liu, Z.; Gao, Z.; Zhang, X. Regular and irregular vegetation pattern formation in semiarid regions: A study on discrete Klausmeier model. Complexity 2020, 2020, 2498073. [Google Scholar] [CrossRef]
- Goldschmidt, F.; Caduff, L.; Johnson, D. Causes and consequences of pattern diversification in a spatially self-organizing microbial community. ISME J. 2021, 15, 2415–2426. [Google Scholar] [CrossRef]
- Schweisguth, F.; Corson, F. Self-organization in pattern formation. Dev. Cell 2019, 49, 659–677. [Google Scholar] [CrossRef]
- Landge, A.N.; Jordan, B.M.; Diego, X.; Müller, P. Pattern formation mechanisms of self-organizing reaction-diffusion systems. Dev. Biol. 2020, 460, 2–11. [Google Scholar] [CrossRef]
- Béguin, C.; Brunetti, M.; Kasparian, J. Quantitative analysis of self-organized patterns in ombrotrophic peatlands. Sci. Rep. 2019, 9, 1499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinto, M.R.; Costa, G.F.; Machado, E.G.; Nagao, R. Self-organization in electrochemical synthesis as a methodology towards new materials. ChemElectroChem 2020, 7, 2979–3005. [Google Scholar] [CrossRef]
- Trelles, J. Pattern formation and self-organization in plasmas interacting with surfaces. J. Phys. D Appl. Phys. 2016, 49, 393002. [Google Scholar] [CrossRef] [Green Version]
- Ta, H.Q.; Bachmatiuk, A.; Mendes, R.G.; Perello, D.J.; Zhao, L.; Trzebicka, B.; Gemming, T.; Rotkin, S.V.; Rümmeli, M.H. Large-area single-crystal graphene via self-organization at the macroscale. Adv. Mater. 2020, 32, 2002755. [Google Scholar] [CrossRef]
- Opsomer, E.; Merminod, S.; Schockmel, J.; Vandewalle, N.; Berhanu, M.; Falcon, E. Patterns in magnetic granular media at the crossover from two to three dimensions. Phys. Rev. E 2020, 102, 042907. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Liu, Y.; He, R.; Zhao, J.; Wang, G.; Yang, G. Self-organized compound pattern and pulsation of dissipative solitons in a passively mode-locked fiber laser. Opt. Lett. 2018, 43, 478–481. [Google Scholar] [CrossRef] [Green Version]
- Ishida, T. Possibility of controlling self-organized patterns with totalistic cellular automata consisting of both rules like game of life and rules producing Turing patterns. Micromachines 2018, 9, 339. [Google Scholar] [CrossRef] [Green Version]
- Coppola, M.; Guo, J.; Gill, E.; Croon, G. Provable self-organizing pattern formation by a swarm of robots with limited knowledge. Swarm Intell. 2019, 13, 59–94. [Google Scholar] [CrossRef] [Green Version]
- Ishida, T. Emergence of Turing patterns in a simple cellular automata-like model via exchange of integer values between adjacent cells. Discrete Dyn. Nat. Soc. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Garzón-Alvarado, D.; Ramírez Martinez, A. A biochemical hypothesis on the formation of fingerprints using a Turing patterns approach. Theor. Biol. Med. Model. 2011, 8, 24. [Google Scholar] [CrossRef] [Green Version]
- Ziaukas, P.; Ragulskis, T.; Ragulskis, M. Communication scheme based on evolutionary spatial 2 × 2 games. Phys. A 2014, 403, 177–188. [Google Scholar] [CrossRef]
- Vaidelys, M.; Ziaukas, P.; Ragulskis, M. Competitively coupled maps for hiding secret visual information. Phys. A 2016, 443, 91–97. [Google Scholar] [CrossRef]
- Vaidelys, M.; Lu, C.; Cheng, Y.; Ragulskis, M. Digital image communication scheme based on the breakup of spiral waves. Phys. A 2017, 467, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Lin, Y.; Zhang, L.; Rao, F.; Tan, Y. Complex patterns in a predator–prey model with self and cross-diffusion. Commun. Nonlinear Sci. 2011, 16, 2006–2015. [Google Scholar] [CrossRef]
- Saunoriene, L.; Ragulskis, M. Secure steganographic communication algorithm based on self-organizing patterns. Phys. Rev. E 2011, 84, 056213. [Google Scholar] [CrossRef] [PubMed]
- Saunoriene, L.; Ragulskis, M.; Cao, J.; Sanjuán, M.A.F. Wada index based on the weighted and truncated Shannon entropy. Nonlinear Dyn. 2021, 104, 739–751. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inform. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef] [Green Version]
- Ilunga, M. Shannon entropy for measuring spatial complexity associated with mean annual runoff of tertiary catchments of the Middle Vaal basin in South Africa. Entropy 2019, 21, 366. [Google Scholar] [CrossRef] [Green Version]
- Yoneyama, K. Theory of continuous set of points (not finished). Tohoku Math. J. First Ser. 1917, 12, 43–158. [Google Scholar]
- Nusse, H.E.; Yorke, J.A. Wada basin boundaries and basin cells. Phys. D 1996, 90, 242–261. [Google Scholar] [CrossRef]
- Daza, A.; Wagemakers, A.; Sanjuán, M.A.F.; Yorke, J.A. Testing for basins of Wada. Sci. Rep. 2015, 5, 16579. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagemakers, A.; Daza, A.; Sanjuán, M.A.F. How to detect Wada basins. Discrete Cont. Dyn.-B 2021, 26, 717–739. [Google Scholar] [CrossRef]
- Witte, R.S.; Witte, J.S. Statistics, 11th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; p. 496. [Google Scholar]
- Fridrich, J.; Goljan, M.; Du, R. Detecting LSB steganography in color, and gray-scale images. IEEE Multimed. 2001, 8, 22–28. [Google Scholar] [CrossRef] [Green Version]
- Petrauskiene, V.; Palivonaite, R.; Aleksa, A.; Ragulskis, M. Dynamic visual cryptography based on chaotic oscillations. Commun. Nonlinear Sci. 2014, 19, 112–120. [Google Scholar] [CrossRef]
- Palevicius, P.; Ragulskis, M. Image communication scheme based on dynamic visual cryptography and computer generated holography. Opt. Commun. 2015, 335, 161–167. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evolut. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H. Ubiquity Symposium: Evolutionary Computation and the Processes of Life: What the No Free Lunch Theorems Really Mean: How to Improve Search Algorithms. Ubiquity 2013, 2013, 1–15. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saunoriene, L.; Jablonskaite, K.; Ragulskiene, J.; Ragulskis, M. Information Hiding Based on Statistical Features of Self-Organizing Patterns. Entropy 2022, 24, 684. https://doi.org/10.3390/e24050684
Saunoriene L, Jablonskaite K, Ragulskiene J, Ragulskis M. Information Hiding Based on Statistical Features of Self-Organizing Patterns. Entropy. 2022; 24(5):684. https://doi.org/10.3390/e24050684
Chicago/Turabian StyleSaunoriene, Loreta, Kamilija Jablonskaite, Jurate Ragulskiene, and Minvydas Ragulskis. 2022. "Information Hiding Based on Statistical Features of Self-Organizing Patterns" Entropy 24, no. 5: 684. https://doi.org/10.3390/e24050684
APA StyleSaunoriene, L., Jablonskaite, K., Ragulskiene, J., & Ragulskis, M. (2022). Information Hiding Based on Statistical Features of Self-Organizing Patterns. Entropy, 24(5), 684. https://doi.org/10.3390/e24050684






