Asymptotic Normality for Plug-In Estimators of Generalized Shannon’s Entropy
Abstract
:1. Introduction
1.1. Introduction and Related Work
1.2. Summary and Contribution
2. Main Results
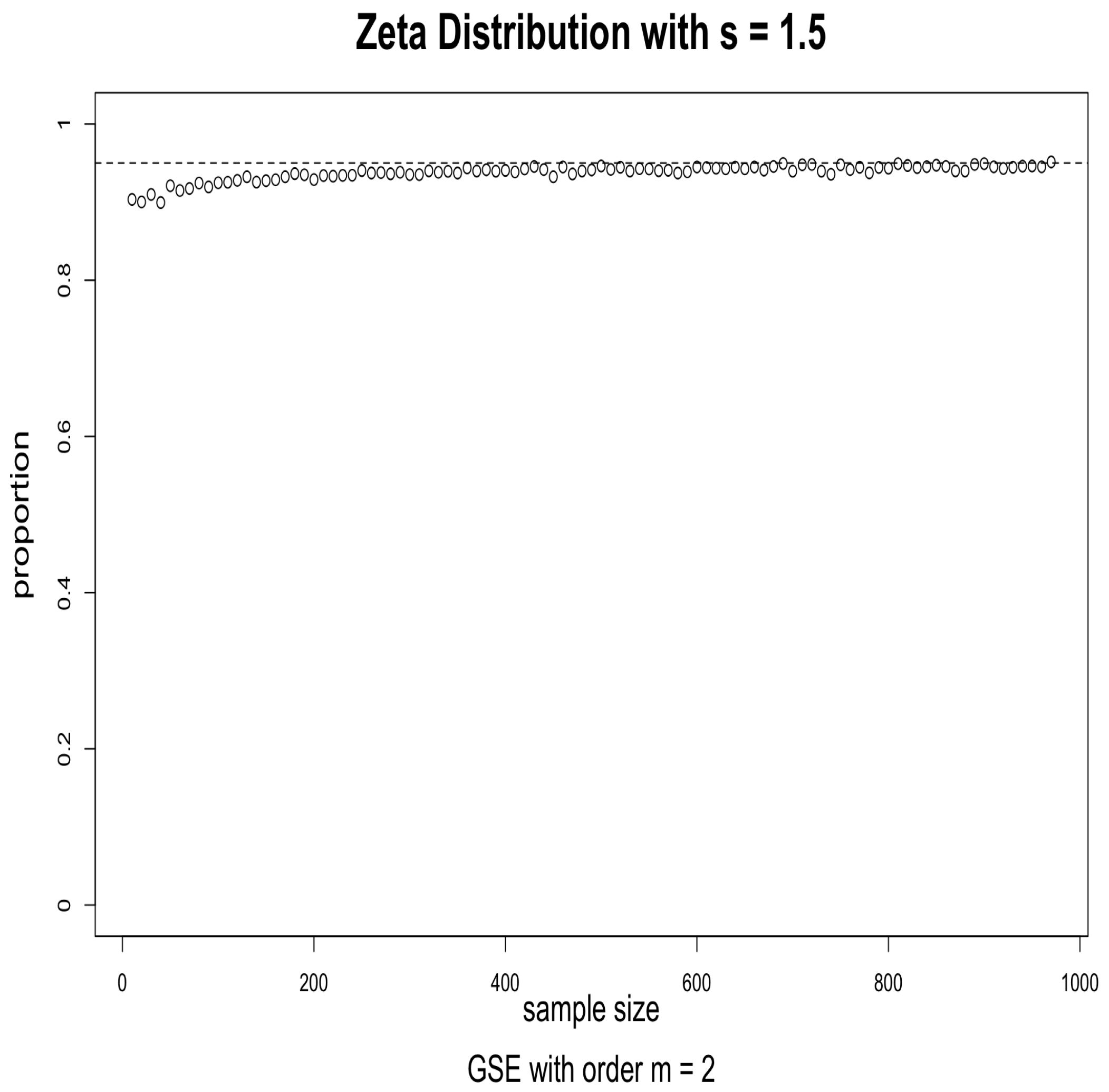
3. Simulations
4. Discussion
5. Proofs
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDOTC | Conditional Distribution of Total Collision |
| GMI | Generalized Mutual Information |
| GSE | Generalized Shannon’s Entropy |
| ML | Machine Learning |
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Banerjee, M.; Reynolds, E.; Andersson, H.B.; Nallamothu, B.K. Tree-based analysis: A practical approach to create clinical decision-making tools. Circ. Cardiovasc. Qual. Outcomes 2019, 12, e004879. [Google Scholar] [CrossRef] [PubMed]
- Mienye, I.D.; Sun, Y.; Wang, Z. Prediction performance of improved decision tree-based algorithms: A review. Procedia Manuf. 2019, 35, 698–703. [Google Scholar] [CrossRef]
- Hssina, B.; Merbouha, A.; Ezzikouri, H.; Erritali, M. A comparative study of decision tree ID3 and C4. 5. Int. J. Adv. Comput. Sci. Appl. 2014, 4, 13–19. [Google Scholar]
- Miller, G.A.; Madow, W.G. On the Maximum Likelihood Estimate of the Shannon-Weiner Measure of Information; Operational Applications Laboratory, Air Force Cambridge Research Center: Bedford, MA, USA, 1954. [Google Scholar]
- Harris, B. The Statistical Estimation of Entropy in the Non-Parametric Case; Technical Report; Wisconsin Univ-Madison Mathematics Research Center: Madison, WI, USA, 1975. [Google Scholar]
- Esty, W.W. A normal limit law for a nonparametric estimator of the coverage of a random sample. Ann. Stat. 1983, 11, 905–912. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Entropy estimation in Turing’s perspective. Neural Comput. 2012, 24, 1368–1389. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, X. A normal law for the plug-in estimator of entropy. IEEE Trans. Inf. Theory 2012, 58, 2745–2747. [Google Scholar] [CrossRef]
- Zhang, Z. Asymptotic normality of an entropy estimator with exponentially decaying bias. IEEE Trans. Inf. Theory 2013, 59, 504–508. [Google Scholar] [CrossRef]
- Baccetti, V.; Visser, M. Infinite shannon entropy. J. Stat. Mech. Theory Exp. 2013, 2013, P04010. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Generalized Mutual Information. Stats 2020, 3, 158–165. [Google Scholar] [CrossRef]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Csiszár, I. Axiomatic characterizations of information measures. Entropy 2008, 10, 261–273. [Google Scholar] [CrossRef] [Green Version]
- Khinchin, A.Y. Mathematical Foundations of Information Theory; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Chakrabarti, C.; Chakrabarty, I. Shannon entropy: Axiomatic characterization and application. Int. J. Math. Math. Sci. 2005, 2005, 2847–2854. [Google Scholar] [CrossRef] [Green Version]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkley, CA, USA, 1 January 1961; University of California Press: Los Angeles, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, C.; Zhang, J. Estimation of population size in entropic perspective. Commun.-Stat.-Theory Methods 2020, 49, 307–324. [Google Scholar] [CrossRef]
- Grabchak, M.; Zhang, Z. Asymptotic normality for plug-in estimators of diversity indices on countable alphabets. J. Nonparametr. Stat. 2018, 30, 774–795. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Shi, J. Asymptotic Normality for Plug-In Estimators of Generalized Shannon’s Entropy. Entropy 2022, 24, 683. https://doi.org/10.3390/e24050683
Zhang J, Shi J. Asymptotic Normality for Plug-In Estimators of Generalized Shannon’s Entropy. Entropy. 2022; 24(5):683. https://doi.org/10.3390/e24050683
Chicago/Turabian StyleZhang, Jialin, and Jingyi Shi. 2022. "Asymptotic Normality for Plug-In Estimators of Generalized Shannon’s Entropy" Entropy 24, no. 5: 683. https://doi.org/10.3390/e24050683
APA StyleZhang, J., & Shi, J. (2022). Asymptotic Normality for Plug-In Estimators of Generalized Shannon’s Entropy. Entropy, 24(5), 683. https://doi.org/10.3390/e24050683





