Metacognition as a Consequence of Competing Evolutionary Time Scales
Abstract
:1. Introduction
2. Background
2.1. Metacognition from an Evolutionary Perspective
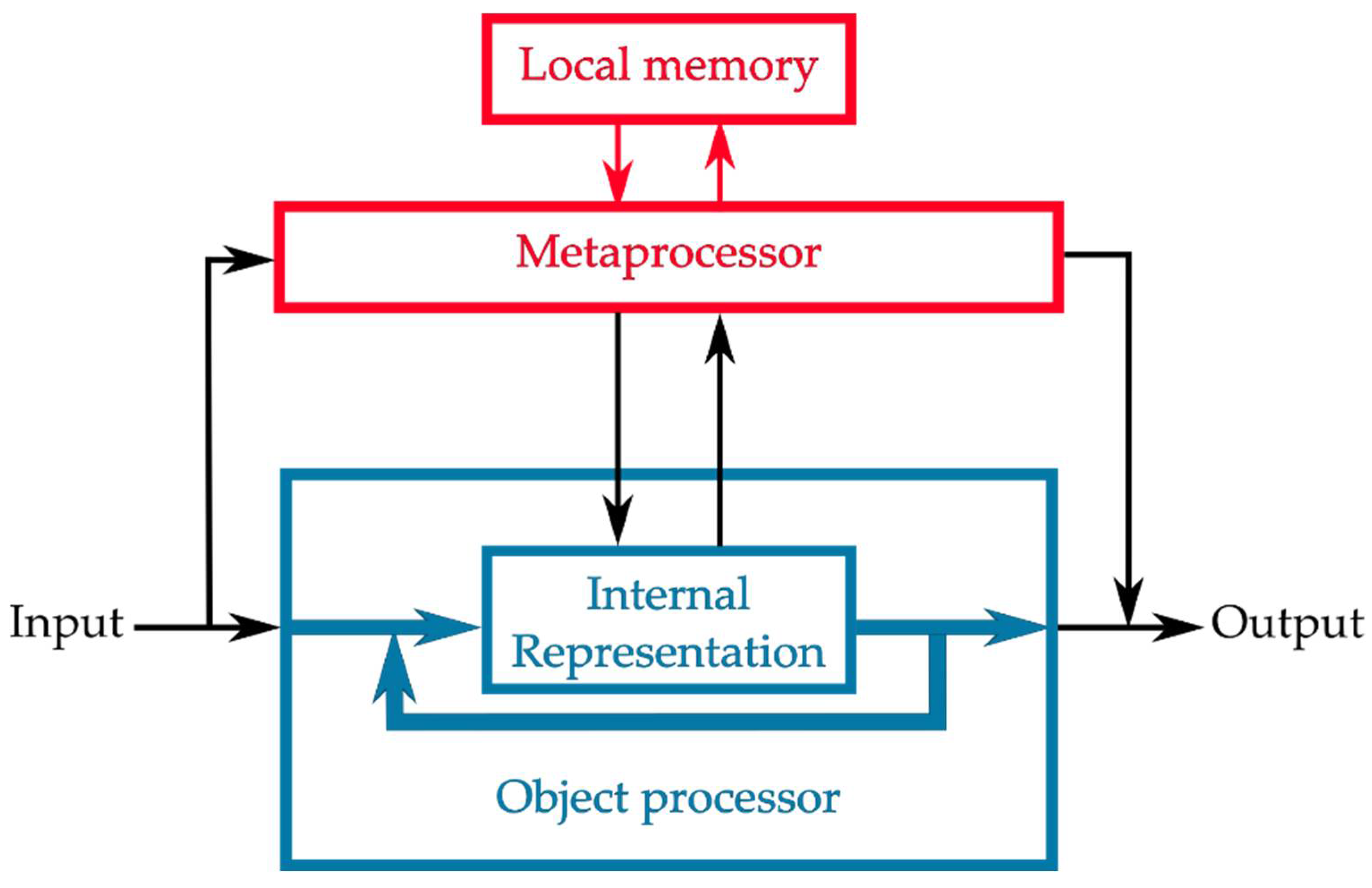
2.2. Computational Resources for Metaprocessing
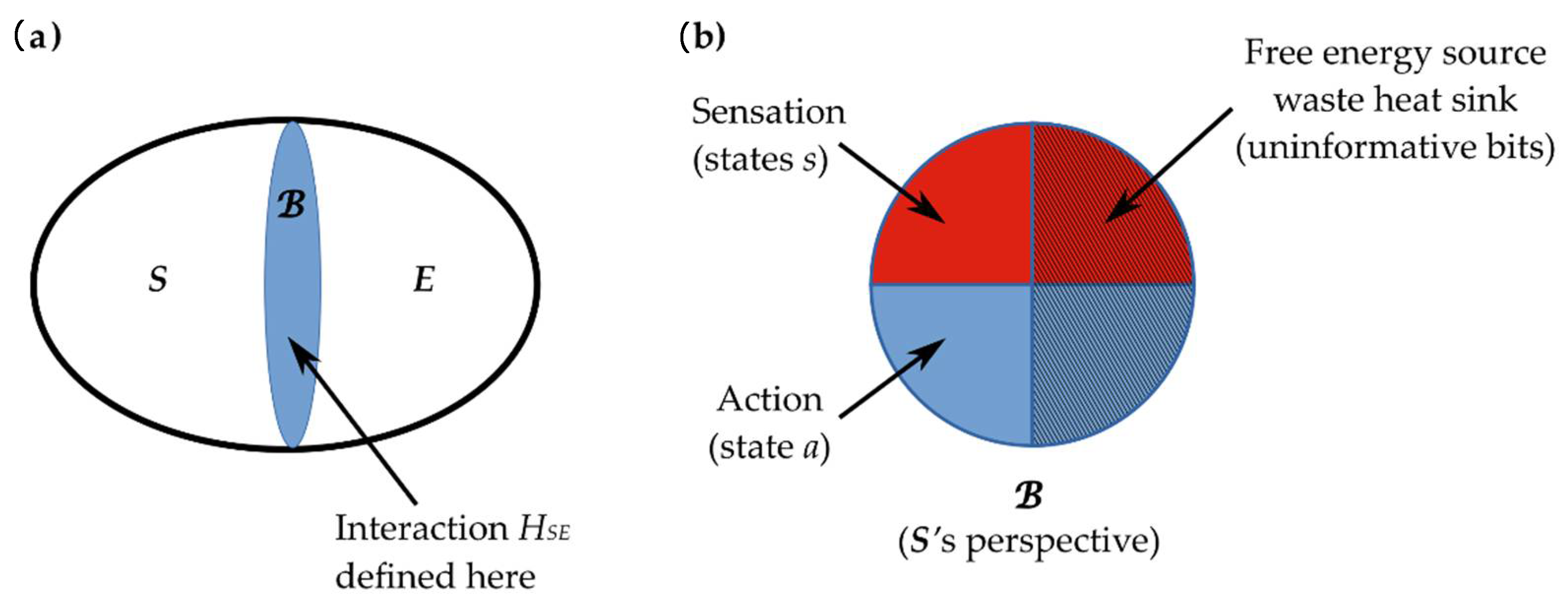
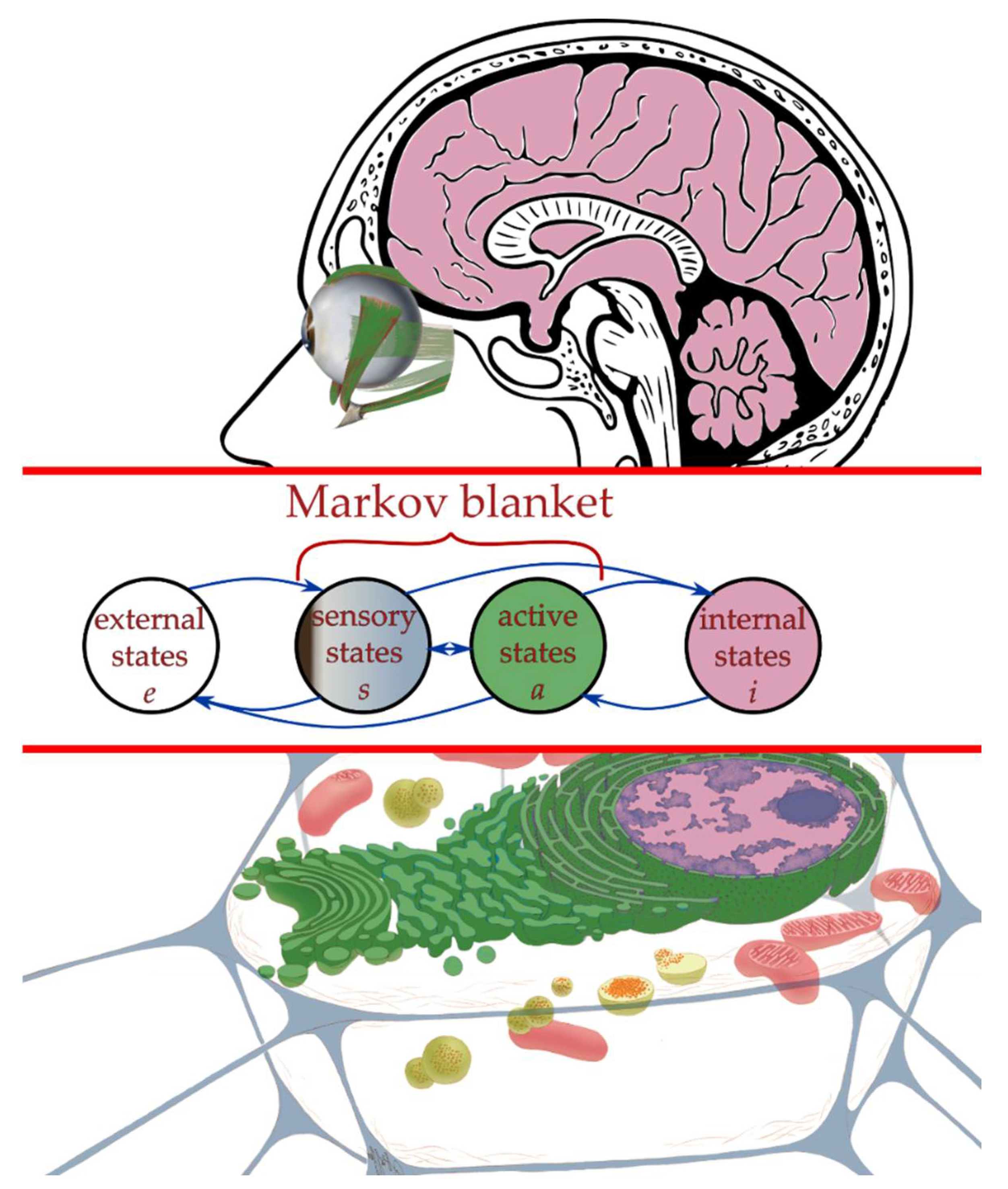
2.3. Interaction across a Markov Blanket
2.4. Active Inference Framework
3. Results
3.1. Formal Investigation of Metacognition in Evolution
3.2. General Models of Two-System Interaction with Selection across Different Time Scales
3.2.1. Multi-Agent Active Inference Networks
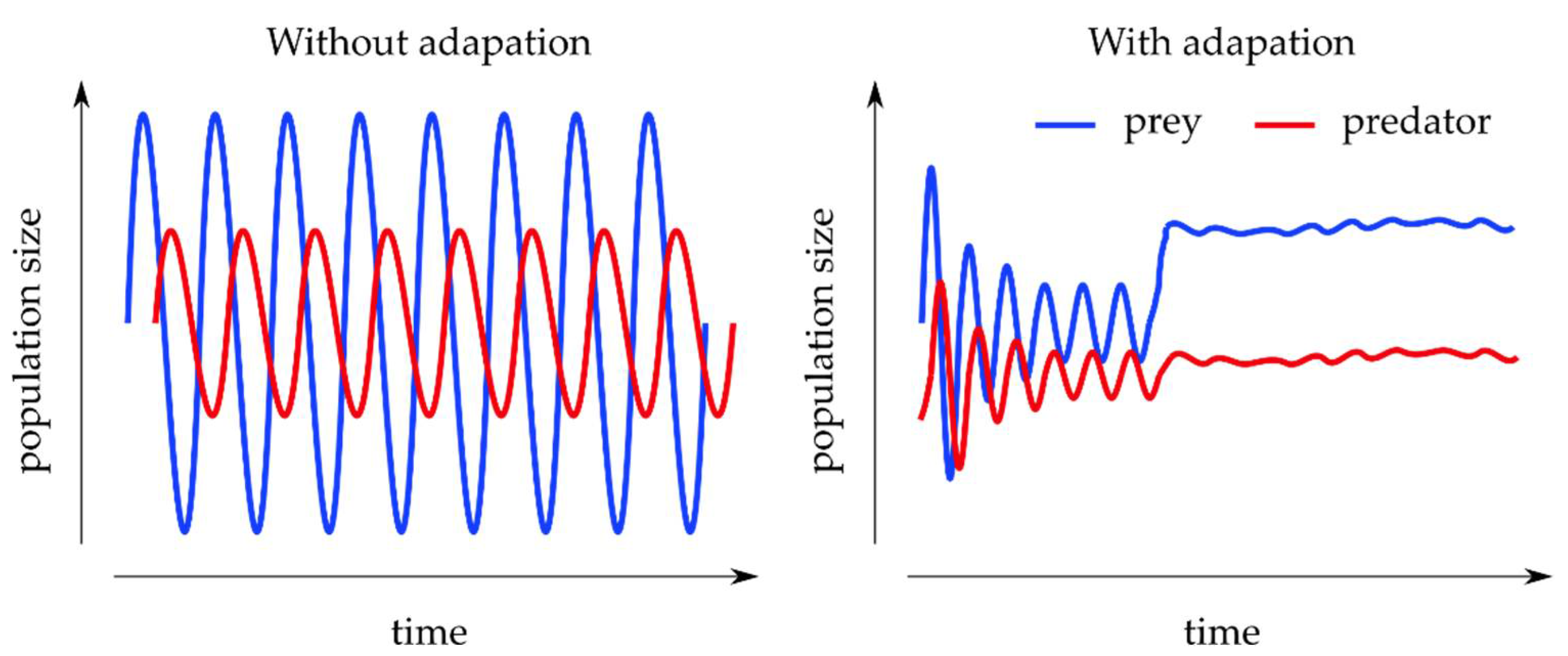
3.2.2. Predator–Prey Models
3.2.3. Coupled Genetic Algorithms
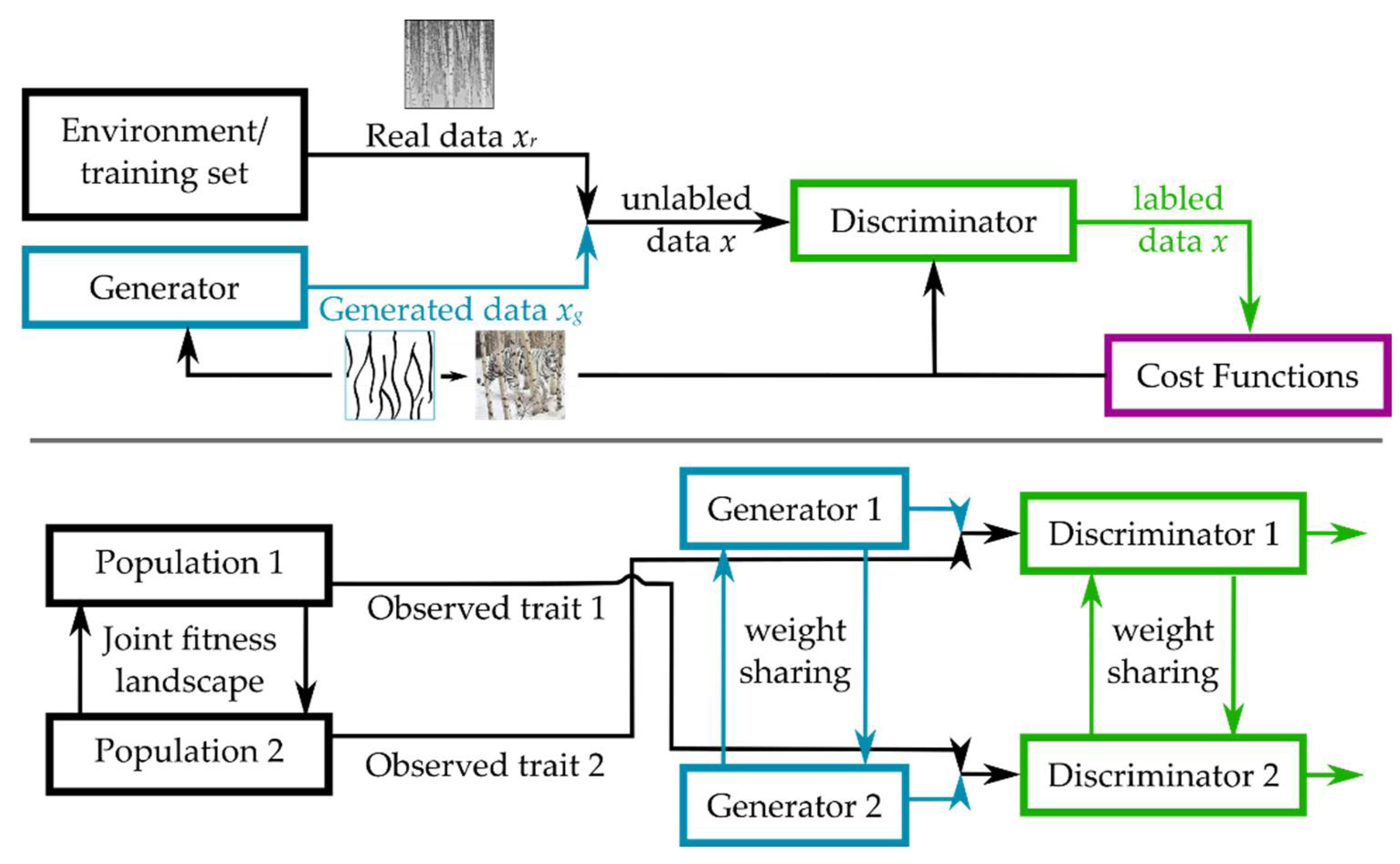
3.2.4. Coupled Generative Adversarial Networks
3.3. Spatio-Temporally Coarse-Grained Structures Emerge Naturally in Any Resource-Limited System with Sufficiently Complex Interaction Dynamics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burgess, P.W.; Wu, H. Rostral prefrontal cortex (Brodmann area 10). In Principles of Frontal Lobe Function; Oxford University Press: New York, NY, USA, 2013; pp. 524–544. [Google Scholar]
- Flavell, J.H. Metacognition and cognitive monitoring: A new area of cognitive–developmental inquiry. Am. Psychol. 1979, 34, 906. [Google Scholar] [CrossRef]
- Fleming, S.M.; Daw, N.D. Self-evaluation of decision-making: A general Bayesian framework for metacognitive computation. Psychol. Rev. 2017, 124, 91. [Google Scholar] [CrossRef]
- Koriat, A.; Levy-Sadot, R. Processes underlying metacognitive judgments: Information-based and experience-based monitoring of one’s own knowledge. In Dual-Process Theories in Social Psychology; The Guilford Press: New York, NY, USA, 1999. [Google Scholar]
- Shea, N.; Frith, C.D. The Global Workspace Needs Metacognition. Trends Cogn. Sci. 2019, 23, 560–571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Winkielman, P.; Schooler, J.W. Consciousness, metacognition, and the unconscious. In The Sage Handbook of Social Cognition; SAGE Publications: London, UK, 2012; pp. 54–74. [Google Scholar]
- Azevedo, R. Reflections on the field of metacognition: Issues, challenges, and opportunities. Metacognition Learn. 2020, 15, 91–98. [Google Scholar] [CrossRef]
- Cox, M.T. Metacognition in computation: A selected research review. Artif. Intell. 2005, 169, 104–141. [Google Scholar] [CrossRef] [Green Version]
- Goertzel, B. Artificial general intelligence: Concept, state of the art, and future prospects. J. Artif. Gen. Intell. 2014, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Kotseruba, I.; Tsotsos, J.K. 40 years of cognitive architectures: Core cognitive abilities and practical applications. Artif. Intell. Rev. 2020, 53, 17–94. [Google Scholar] [CrossRef] [Green Version]
- Sloman, A. Varieties of Metacognition in Natural and Artificial Systems; AAAI Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Drigas, A.; Mitsea, E. 8 Pillars X 8 Layers Model of Metacognition: Educational Strategies, Exercises &Trainings. Int. J. Online Biomed. Eng. IJOE 2021, 17, 115. [Google Scholar] [CrossRef]
- Conant, R.C.; Ross Ashby, W. Every good regulator of a system must be a model of that system. Int. J. Syst. Sci. 1970, 1, 89–97. [Google Scholar] [CrossRef]
- Friedman, N.P.; Robbins, T.W. The role of prefrontal cortex in cognitive control and executive function. Neuropsychopharmacology 2022, 47, 72–89. [Google Scholar] [CrossRef]
- Menon, V.; D’Esposito, M. The role of PFC networks in cognitive control and executive function. Neuropsychopharmacology 2022, 47, 90–103. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.S.B.T. Dual-Processing Accounts of Reasoning, Judgment, and Social Cognition. Annu. Rev. Psychol. 2008, 59, 255–278. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.S.B.T.; Stanovich, K.E. Dual-Process Theories of Higher Cognition. Perspect. Psychol. Sci. 2013, 8, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Chater, N. Mind Is Flat: The Remarkable Shallowness of the Improvising Brain; Yale University Press: London, UK, 2018. [Google Scholar]
- Fields, C.; Glazebrook, J.F. Do Process-1 simulations generate the epistemic feelings that drive Process-2 decision making? Cogn. Processing 2020, 21, 533–553. [Google Scholar] [CrossRef] [PubMed]
- Melnikoff, D.E.; Bargh, J.A. The Mythical Number Two. Trends Cogn. Sci. 2018, 22, 280–293. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F.; Levin, M. Minimal physicalism as a scale-free subtrate for cognition and consciousness. Neurosci. Conscious. 2021, 2021, niab013. [Google Scholar] [CrossRef] [PubMed]
- Baron, S.; Eisenbach, M. CheY acetylation is required for ordinary adaptation time inEscherichia colichemotaxis. FEBS Lett. 2017, 591, 1958–1965. [Google Scholar] [CrossRef] [Green Version]
- Fields, C.; Levin, M. Multiscale memory and bioelectric error correction in the cytoplasm-cytoskeleton-membrane system. Wiley Interdiscip. Rev. Syst. Biol. Med. 2018, 10, e1410. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- Clark, A. How to knit your own Markov blanket. In Philosophy and Predictive Processing; The Free Press: New York, NY, USA, 2017. [Google Scholar]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.; Levin, M.; Sengupta, B.; Pezzulo, G. Knowing one’s place: A free-energy approach to pattern regulation. J. R. Soc. Interface 2015, 12, 20141383. [Google Scholar] [CrossRef] [Green Version]
- Kirchhoff, M.; Parr, T.; Palacios, E.; Friston, K.; Kiverstein, J. The Markov blankets of life: Autonomy, active inference and the free energy principle. J. R. Soc. Interface 2018, 15, 20170792. [Google Scholar] [CrossRef]
- Kuchling, F.; Friston, K.; Georgiev, G.; Levin, M. Morphogenesis as Bayesian inference: A variational approach to pattern formation and control in complex biological systems. Phys. Life Rev. 2019, 33, 88–108. [Google Scholar] [CrossRef]
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar]
- Fields, C.; Friston, K.; Glazebrook, J.F.; Levin, M. A free energy principle for generic quantum systems. arXiv 2021, arXiv:2112.15242. [Google Scholar]
- Sattin, D.; Magnani, F.G.; Bartesaghi, L.; Caputo, M.; Fittipaldo, A.V.; Cacciatore, M.; Picozzi, M.; Leonardi, M. Theoretical Models of Consciousness: A Scoping Review. Brain Sci. 2021, 11, 535. [Google Scholar] [CrossRef] [PubMed]
- Signorelli, C.M.; Szczotka, J.; Prentner, R. Explanatory profiles of models of consciousness-towards a systematic classification. Neurosci. Conscious. 2021, 2021, niab021. [Google Scholar] [CrossRef]
- Baars, B.J.; Franklin, S. How conscious experience and working memory interact. Trends Cogn. Sci. 2003, 7, 166–172. [Google Scholar] [CrossRef] [Green Version]
- Dehaene, S.; Changeux, J.-P. Neural mechanisms for access to consciousness. Cogn. Neurosci. 2004, 3, 1145–1158. [Google Scholar]
- Gennaro, R.J. Higher-order theories of consciousness. In The Bloomsbury Companion to the Philosophy of Consciousness; Bloomsbury Publishing: London, UK, 2018; p. 142. [Google Scholar]
- Lau, H. Consciousness, Metacognition, & Perceptual Reality Monitoring. PsyArXiv 2019. [Google Scholar] [CrossRef]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, P.; Ben-Soussan, T.D. Reflections on Inner and Outer Silence and Consciousness Without Contents According to the Sphere Model of Consciousness. Front. Psychol. 2020, 11, 1807. [Google Scholar] [CrossRef]
- Oudeyer, P.-Y.; Kaplan, F. What is intrinsic motivation? A typology of computational approaches. Front. Neurorobotics 2009, 1, 6. [Google Scholar] [CrossRef] [Green Version]
- Gottlieb, J.; Lopes, M.; Oudeyer, P.-Y. Motivated Cognition: Neural and Computational Mechanisms of Curiosity, Attention, and Intrinsic Motivation; Emerald Group Publishing Limited: Bingley, UK, 2016; pp. 149–172. [Google Scholar] [CrossRef] [Green Version]
- Millar, J. An Ethics Evaluation Tool for Automating Ethical Decision-Making in Robots and Self-Driving Cars. Appl. Artif. Intell. 2016, 30, 787–809. [Google Scholar] [CrossRef]
- Smallwood, J.; Bernhardt, B.C.; Leech, R.; Bzdok, D.; Jefferies, E.; Margulies, D.S. The default mode network in cognition: A topographical perspective. Nat. Rev. Neurosci. 2021, 22, 503–513. [Google Scholar] [CrossRef]
- Fleming, S.M.; Huijgen, J.; Dolan, R.J. Prefrontal Contributions to Metacognition in Perceptual Decision Making. J. Neurosci. 2012, 32, 6117–6125. [Google Scholar] [CrossRef] [Green Version]
- Fleming, S.M.; Ryu, J.; Golfinos, J.G.; Blackmon, K.E. Domain-specific impairment in metacognitive accuracy following anterior prefrontal lesions. Brain 2014, 137, 2811–2822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleming, S.M.; Weil, R.S.; Nagy, Z.; Dolan, R.J.; Rees, G. Relating introspective accuracy to individual differences in brain structure. Science 2010, 329, 1541–1543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McCurdy, L.Y.; Maniscalco, B.; Metcalfe, J.; Liu, K.Y.; De Lange, F.P.; Lau, H. Anatomical Coupling between Distinct Metacognitive Systems for Memory and Visual Perception. J. Neurosci. 2013, 33, 1897–1906. [Google Scholar] [CrossRef] [Green Version]
- Ye, Q.; Zou, F.; Dayan, M.; Lau, H.; Hu, Y.; Kwok, S.C. Individual susceptibility to TMS affirms the precuneal role in meta-memory upon recollection. Brain Struct. Funct. 2019, 224, 2407–2419. [Google Scholar] [CrossRef]
- Hampton, R.R. Multiple demonstrations of metacognition in nonhumans: Converging evidence or multiple mechanisms? Comp. Cogn. Behav. Rev. 2009, 4, 17–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Middlebrooks, P.G.; Sommer, M.A. Metacognition in monkeys during an oculomotor task. J. Exp. Psychol. Learn. Mem. Cogn. 2011, 37, 325–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyamoto, K.; Osada, T.; Setsuie, R.; Takeda, M.; Tamura, K.; Adachi, Y.; Miyashita, Y. Causal neural network of metamemory for retrospection in primates. Science 2017, 355, 188–193. [Google Scholar] [CrossRef]
- Miyamoto, K.; Setsuie, R.; Osada, T.; Miyashita, Y. Reversible Silencing of the Frontopolar Cortex Selectively Impairs Metacognitive Judgment on Non-experience in Primates. Neuron 2018, 97, 980–989.e6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, Y.; Jin, Z.; Zhai, C.; Wang, H.; Wang, J.; Tang, Y.; Kwok, S.C. Time-Sensitive Prefrontal Involvement in Associating Confidence with Task Performance Illustrates Metacognitive Introspection in Monkeys; Cold Spring Harbor Laboratory: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Kwok, S.C.; Cai, Y.; Buckley, M.J. Mnemonic Introspection in Macaques Is Dependent on Superior Dorsolateral Prefrontal Cortex But Not Orbitofrontal Cortex. J. Neurosci. 2019, 39, 5922–5934. [Google Scholar] [CrossRef] [PubMed]
- Masset, P.; Ott, T.; Lak, A.; Hirokawa, J.; Kepecs, A. Behavior- and Modality-General Representation of Confidence in Orbitofrontal Cortex. Cell 2020, 182, 112–126.e18. [Google Scholar] [CrossRef]
- Bayne, T.; Brainard, D.; Byrne, R.W.; Chittka, L.; Clayton, N.; Heyes, C.; Mather, J.; Ölveczky, B.; Shadlen, M.; Suddendorf, T.; et al. What is cognition? Curr. Biol. 2019, 29, R608–R615. [Google Scholar] [CrossRef] [PubMed]
- Gallup, G.G., Jr.; Anderson, J.R. Self-recognition in animals: Where do we stand 50 years later? Lessons from cleaner wrasse and other species. Psychol. Conscious. Theory Res. Pract. 2020, 7, 46. [Google Scholar]
- Mather, J. What is in an octopus’s mind? Anim. Sentience 2019, 4, 1. [Google Scholar] [CrossRef]
- Schnell, A.K.; Amodio, P.; Boeckle, M.; Clayton, N.S. How intelligent is a cephalopod? Lessons from comparative cognition. Biol. Rev. 2021, 96, 162–178. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.E.; Ravi, N. The architecture of virtual machines. Computer 2005, 38, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Gottlieb, J.; Oudeyer, P.-Y.; Lopes, M.; Baranes, A. Information-seeking, curiosity, and attention: Computational and neural mechanisms. Trends Cogn. Sci. 2013, 17, 585–593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ten, A.; Kaushik, P.; Oudeyer, P.-Y.; Gottlieb, J. Humans monitor learning progress in curiosity-driven exploration. Nat. Commun. 2021, 12, 5972. [Google Scholar] [CrossRef] [PubMed]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Franklin, S.; Madl, T.; D’Mello, S.; Snaider, J. LIDA: A Systems-level Architecture for Cognition, Emotion, and Learning. IEEE Trans. Auton. Ment. Dev. 2014, 6, 19–41. [Google Scholar] [CrossRef]
- Anderson, J.R. Human Symbol Manipulation Within an Integrated Cognitive Architecture. Cogn. Sci. 2005, 29, 313–341. [Google Scholar] [CrossRef]
- Grossberg, S. Adaptive Resonance Theory: How a brain learns to consciously attend, learn, and recognize a changing world. Neural Netw. 2013, 37, 1–47. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F.; Marcianò, A. Reference Frame Induced Symmetry Breaking on Holographic Screens. Symmetry 2021, 13, 408. [Google Scholar] [CrossRef]
- Addazi, A.; Chen, P.; Fabrocini, F.; Fields, C.; Greco, E.; Lulli, M.; Marciano, A.; Pasechnik, R. Generalized holographic principle, gauge invariance and the emergence of gravity à la Wilczek. Front. Astron. Space Sci. 2021, 8, 1. [Google Scholar] [CrossRef]
- Fields, C.; Marcianò, A. Holographic Screens Are Classical Information Channels. Quantum Rep. 2020, 2, 326–336. [Google Scholar] [CrossRef]
- Fields, C.; Marcianò, A. Markov blankets are general physical interaction surfaces. Phys. Life Rev. 2019, 33, 109–111. [Google Scholar] [CrossRef] [PubMed]
- Fields, C. Some Consequences of the Thermodynamic Cost of System Identification. Entropy 2018, 20, 797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sajid, N.; Convertino, L.; Friston, K. Cancer Niches and Their Kikuchi Free Energy. Entropy 2021, 23, 609. [Google Scholar] [CrossRef] [PubMed]
- Hesp, C.; Ramstead, M.; Constant, A.; Badcock, P.; Kirchhoff, M.; Friston, K. A multi-scale view of the emergent complexity of life: A free-energy proposal. In Evolution, Development and Complexity; Springer: Berlin/Heidelberg, Germany, 2019; pp. 195–227. [Google Scholar]
- Constant, A.; Ramstead, M.J.D.; Veissière, S.P.L.; Campbell, J.O.; Friston, K.J. A variational approach to niche construction. J. R. Soc. Interface 2018, 15, 20170685. [Google Scholar] [CrossRef] [PubMed]
- Bruineberg, J.; Rietveld, E.; Parr, T.; Van Maanen, L.; Friston, K.J. Free-energy minimization in joint agent-environment systems: A niche construction perspective. J. Theor. Biol. 2018, 455, 161–178. [Google Scholar] [CrossRef]
- Friston, K. A Free Energy Principle for Biological Systems. Entropy 2012, 14, 2100–2121. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Somatic multicellularity as a satisficing solution to the prediction-error minimization problem. Commun. Integr. Biol. 2019, 12, 119–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.; Parr, T.; Zeidman, P. Bayesian model reduction. arXiv 2018, arXiv:1805.07092. [Google Scholar]
- Campbell, J.O. Universal Darwinism As a Process of Bayesian Inference. Front. Syst. Neurosci. 2016, 10, 49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fisher, R.A. The Genetical Theory of Natural Selection; Oxford: London, UK, 1930. [Google Scholar]
- Frank, S.A. Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. J. Evol. Biol. 2012, 25, 2377–2396. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Does Evolution Have a Target Morphology? Organisms. J. Biol. Sci. 2020, 4, 57–76. [Google Scholar]
- Pezzulo, G.; Parr, T.; Friston, K. The evolution of brain architectures for predictive coding and active inference. Philos. Trans. R. Soc. B 2022, 377, 20200531. [Google Scholar] [CrossRef] [PubMed]
- Ueltzhöffer, K. Deep active inference. Biol. Cybern. 2018, 112, 547–573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landauer, R. Information is a physical entity. Phys. A Stat. Mech. Its Appl. 1999, 263, 63–67. [Google Scholar] [CrossRef] [Green Version]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Fields, C. Trajectory Recognition as the Basis for Object Individuation: A Functional Model of Object File Instantiation and Object-Token Encoding. Front. Psychol. 2011, 2, 49. [Google Scholar] [CrossRef] [Green Version]
- Aquino, G.; Endres, R.G. Increased accuracy of ligand sensing by receptor internalization. Phys. Rev. E 2010, 81, 021909. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Cremer, P.S.; Manson, M.D. A sensitive, versatile microfluidic assay for bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 2003, 100, 5449–5454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berg, H. Random Walks in Biology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Mukherjee, S.; Ghosh, R.N.; Maxfield, F.R. Endocytosis. Physiol. Rev. 1997, 77, 759–803. [Google Scholar] [CrossRef]
- Mehta, P.; Lang, A.H.; Schwab, D.J. Landauer in the Age of Synthetic Biology: Energy Consumption and Information Processing in Biochemical Networks. J. Stat. Phys. 2016, 162, 1153–1166. [Google Scholar] [CrossRef] [Green Version]
- Mehta, P.; Schwab, D.J. Energetic costs of cellular computation. Proc. Natl. Acad. Sci. USA 2012, 109, 17978–17982. [Google Scholar] [CrossRef] [Green Version]
- Karpathy, A.; Johnson, J.; Fei-Fei, L. Visualizing and Understanding Recurrent Networks. arXiv 2015, arXiv:1506.02078. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hansen, N.; Arnold, D.V.; Auger, A. Evolution Strategies; Springer: Berlin/Heidelberg, Germany, 2015; pp. 871–898. [Google Scholar] [CrossRef]
- Hesp, C.; Smith, R.; Parr, T.; Allen, M.; Friston, K.J.; Ramstead, M.J.D. Deeply Felt Affect: The Emergence of Valence in Deep Active Inference. Neural Comput. 2021, 33, 398–446. [Google Scholar] [CrossRef]
- Lyon, P.; Kuchling, F. Valuing what happens: A biogenic approach to valence and (potentially) affect. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2021, 376, 20190752. [Google Scholar] [CrossRef]
- Levin, M. Life, death, and self: Fundamental questions of primitive cognition viewed through the lens of body plasticity and synthetic organisms. Biochem. Biophys. Res. Commun. 2021, 564, 114–133. [Google Scholar] [CrossRef]
- Lotka, A.J. Contribution to the Theory of Periodic Reactions. J. Phys. Chem. 1910, 14, 271–274. [Google Scholar] [CrossRef] [Green Version]
- Cortez, M.H.; Weitz, J.S. Coevolution can reverse predator-prey cycles. Proc. Natl. Acad. Sci. USA 2014, 111, 7486–7491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poggiale, J.-C.; Aldebert, C.; Girardot, B.; Kooi, B.W. Analysis of a predator–prey model with specific time scales: A geometrical approach proving the occurrence of canard solutions. J. Math. Biol. 2020, 80, 39–60. [Google Scholar] [CrossRef] [Green Version]
- Vanselow, A.; Wieczorek, S.; Feudel, U. When very slow is too fast-collapse of a predator-prey system. J. Theor. Biol. 2019, 479, 64–72. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lee, J.; Kim, T.; Ahn, I.; Park, J. Co-Evolution of Predator-Prey Ecosystems by Reinforcement Learning Agents. Entropy 2021, 23, 461. [Google Scholar] [CrossRef] [PubMed]
- Rosenzweig, M.L.; MacArthur, R.H. Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 1963, 97, 209–223. [Google Scholar] [CrossRef]
- Velzen, E. Predator coexistence through emergent fitness equalization. Ecology 2020, 101, e02995. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Auger, P.; Kooi, B.W.; Bravo De La Parra, R.; Poggiale, J.-C. Bifurcation analysis of a predator–prey model with predators using hawk and dove tactics. J. Theor. Biol. 2006, 238, 597–607. [Google Scholar] [CrossRef] [PubMed]
- Cortez, M.H.E.; Stephen, P. Understanding Rapid Evolution in Predator-Prey Interactions Using the Theory of Fast-Slow Dynamical Systems. Am. Nat. 2010, 176, E109–E127. [Google Scholar] [CrossRef]
- Romero-Muñoz, A.; Maffei, L.; Cuéllar, E.; Noss, A.J. Temporal separation between jaguar and puma in the dry forests of southern Bolivia. J. Trop. Ecol. 2010, 26, 303–311. [Google Scholar] [CrossRef]
- Karanth, K.U.; Sunquist, M.E. Behavioural correlates of predation by tiger (Panthera tigris), leopard (Panthera pardus) and dhole (Cuon alpinus) in Nagarahole, India. J. Zool. 2000, 250, 255–265. [Google Scholar] [CrossRef]
- Martin, A.; Simon, C. Temporal Variation in Insect Life Cycles. BioScience 1990, 40, 359–367. [Google Scholar] [CrossRef]
- Kingsolver, J.G.; Arthur Woods, H.; Buckley, L.B.; Potter, K.A.; Maclean, H.J.; Higgins, J.K. Complex Life Cycles and the Responses of Insects to Climate Change. Integr. Comp. Biol. 2011, 51, 719–732. [Google Scholar] [CrossRef] [Green Version]
- Laan, J.D.V.D.; Hogeweg, P. Predator—prey coevolution: Interactions across different timescales. Proc. R. Soc. London. Ser. B Biol. Sci. 1995, 259, 35–42. [Google Scholar] [CrossRef]
- Bosiger, Y.J.; Lonnstedt, O.M.; McCormick, M.I.; Ferrari, M.C.O. Learning Temporal Patterns of Risk in a Predator-Diverse Environment. PLoS ONE 2012, 7, e34535. [Google Scholar] [CrossRef] [PubMed]
- Ishii, Y.; Shimada, M. The effect of learning and search images on predator–prey interactions. Popul. Ecol. 2010, 52, 27–35. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, J.; Wang, L. A reinforcement learning-based predator-prey model. Ecol. Complex. 2020, 42, 100815. [Google Scholar] [CrossRef]
- Yamada, J.; Shawe-Taylor, J.; Fountas, Z. Evolution of a Complex Predator-Prey Ecosystem on Large-scale Multi-Agent Deep Reinforcement Learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Wilson, E.; Morgan, T. Chiasmatype and crossing over. Am. Nat. 1920, 54, 193–219. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Forrest, S. Genetic algorithms: Principles of natural selection applied to computation. Science 1993, 261, 872–878. [Google Scholar] [CrossRef] [Green Version]
- Forrest, S. Genetic algorithms. ACM Comput. Surv. CSUR 1996, 28, 77–80. [Google Scholar] [CrossRef]
- Forrest, S.; Mitchell, M. What makes a problem hard for a genetic algorithm? Some anomalous results and their explanation. Mach. Learn. 1993, 13, 285–319. [Google Scholar]
- Shrestha, A.; Mahmood, A. Improving Genetic Algorithm with Fine-Tuned Crossover and Scaled Architecture. J. Math. 2016, 2016, 4015845. [Google Scholar] [CrossRef] [Green Version]
- Prentis, P.J.; Wilson, J.R.U.; Dormontt, E.E.; Richardson, D.M.; Lowe, A.J. Adaptive evolution in invasive species. Trends Plant Sci. 2008, 13, 288–294. [Google Scholar] [CrossRef] [PubMed]
- Kazarlis, S.; Petridis, V. Varying Fitness Functions in Genetic Algorithms: Studying the Rate of Increase of the Dynamic Penalty Terms; Springer: Berlin/Heidelberg, Germany, 1998; pp. 211–220. [Google Scholar] [CrossRef]
- Jin, Y.; Branke, J. Evolutionary Optimization in Uncertain Environments—A Survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Handa, H. Fitness Function for Finding out Robust Solutions on Time-Varying Functions; ACM Press: New York, NY, USA, 2006. [Google Scholar]
- Bull, L. On coevolutionary genetic algorithms. Soft Comput. 2001, 5, 201–207. [Google Scholar] [CrossRef]
- Bull, L. Coevolutionary Species Adaptation Genetic Algorithms: A Continuing SAGA on Coupled Fitness Landscapes; Springer: Berlin/Heidelberg, Germany, 2005; pp. 322–331. [Google Scholar] [CrossRef]
- Bull, L. Coevolutionary species adaptation genetic algorithms: Growth and mutation on coupled fitness landscapes. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; pp. 559–564. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Coevolutionary Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 223–229. [Google Scholar] [CrossRef]
- Paredis, J. Coevolution, Memory and Balance. IJCAI 1999, 10, 1212–1217. [Google Scholar]
- Mitchell, W.A. Multi-behavioral strategies in a predator-prey game: An evolutionary algorithm analysis. Oikos 2009, 118, 1073–1083. [Google Scholar] [CrossRef]
- Paredis, J. Coevolutionary computation. Artif. Life 1995, 2, 355–375. [Google Scholar] [CrossRef]
- Kauffman, S.A.; Johnsen, S. Coevolution to the edge of chaos: Coupled fitness landscapes, poised states, and coevolutionary avalanches. J. Theor. Biol. 1991, 149, 467–505. [Google Scholar] [CrossRef]
- Gonog, L.; Zhou, Y. A Review: Generative Adversarial Networks. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019. [Google Scholar]
- Talas, L.; Fennell, J.G.; Kjernsmo, K.; Cuthill, I.C.; Scott-Samuel, N.E.; Baddeley, R.J. CamoGAN: Evolving optimum camouflage with Generative Adversarial Networks. Methods Ecol. Evol. 2020, 11, 240–247. [Google Scholar] [CrossRef]
- Liu, M.-Y.; Tuzel, O. Coupled generative adversarial networks. Adv. Neural Inf. Processing Syst. 2016, 29, 469–477. [Google Scholar]
- Wang, J.; Jiang, J. Conditional Coupled Generative Adversarial Networks for Zero-Shot Domain Adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Qi, M.; Wang, Y.; Li, A.; Luo, J. STC-GAN: Spatio-Temporally Coupled Generative Adversarial Networks for Predictive Scene Parsing. IEEE Trans. Image Processing 2020, 29, 5420–5430. [Google Scholar] [CrossRef]
- Levin, M. The wisdom of the body: Future techniques and approaches to morphogenetic fields in regenerative medicine, developmental biology and cancer. Regen. Med. 2011, 6, 667–673. [Google Scholar] [CrossRef] [Green Version]
- Levin, M. Morphogenetic fields in embryogenesis, regeneration, and cancer: Non-local control of complex patterning. Biosystems 2012, 109, 243–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watson, R.A.; Szathmáry, E. How Can Evolution Learn? Trends Ecol. Evol. 2016, 31, 147–157. [Google Scholar] [CrossRef] [Green Version]
- Kashtan, N.; Alon, U. Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. USA 2005, 102, 13773–13778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parter, M.; Kashtan, N.; Alon, U. Facilitated Variation: How Evolution Learns from Past Environments To Generalize to New Environments. PLoS Comput. Biol. 2008, 4, e1000206. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Scale-Free Biology: Integrating Evolutionary and Developmental Thinking. BioEssays 2020, 42, 1900228. [Google Scholar] [CrossRef]
- Tauber, C.A.; Tauber, M.J. Insect seasonal cycles: Genetics and evolution. Annu. Rev. Ecol. Syst. 1981, 12, 281–308. [Google Scholar] [CrossRef]
- Lathe, R. Fast tidal cycling and the origin of life. Icarus 2004, 168, 18–22. [Google Scholar] [CrossRef]
- Gordon, R.; Mikhailovsky, G. There were plenty of day/night cycles that could have accelerated an origin of life on Earth, without requiring panspermia. In Planet Formation and Panspermia: New Prospects for the Movement of Life through Space; Wiley: Hoboken, NJ, USA, 2021; pp. 195–206. [Google Scholar]
- Gehring, W.; Rosbash, M. The coevolution of blue-light photoreception and circadian rhythms. J. Mol. Evol. 2003, 57, S286–S289. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchling, F.; Fields, C.; Levin, M. Metacognition as a Consequence of Competing Evolutionary Time Scales. Entropy 2022, 24, 601. https://doi.org/10.3390/e24050601
Kuchling F, Fields C, Levin M. Metacognition as a Consequence of Competing Evolutionary Time Scales. Entropy. 2022; 24(5):601. https://doi.org/10.3390/e24050601
Chicago/Turabian StyleKuchling, Franz, Chris Fields, and Michael Levin. 2022. "Metacognition as a Consequence of Competing Evolutionary Time Scales" Entropy 24, no. 5: 601. https://doi.org/10.3390/e24050601
APA StyleKuchling, F., Fields, C., & Levin, M. (2022). Metacognition as a Consequence of Competing Evolutionary Time Scales. Entropy, 24(5), 601. https://doi.org/10.3390/e24050601






