A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records
Abstract
:1. Introduction
1.1. Motivation
1.2. Missing Data Classification
1.3. Endeavours to Impute Missing Data
1.4. Importance of Imputing Missing Health Data for Entropy
1.5. Research Contributions
- We introduce a unique Ensemble Strategy for Missing Value to analyse healthcare data with considerable missing values to identify unbiased and accurate prediction statistical modelling. Overall, there are four computational benefits of the suggested model:
- It can analyse huge amounts of health data with substantial missing values and impute them more correctly than standalone imputation procedures such as the k-nearest neighbour approach, iterative method, and so on.
- It can discover essential characteristics in a dataset with many missing values.
- It tackles the performance glitches of developing a single predictor to impute missing values, such as high variance, feature bias, and lack of precision.
- Fundamentally, it employs an extreme gradient-boosting method, which includes L1 (Lasso Regression) and L2 (Ridge Regression) regularisation to avoid overfitting.
- The current study uses real-world healthcare data (snapshot presented in Figure 1) to conduct experiments and simulations of data with varying feature-wise missing frequencies indicating that the proposed technique surpasses standard missing value imputation approaches.
2. Related Work
- High variance is achieved by rendering the model supersensitive to the inputs given to the acquired characteristics.
- Inaccuracy due to fitting the intensive training data with a single model or technique may not be sufficient to satisfy expectations.
- When making predictions, noise and bias cause the models to rely mainly on one or a few features.
3. Materials and Methods
- Data pre-processing
- Model training
- Imputation
3.1. Data Pre-Processing
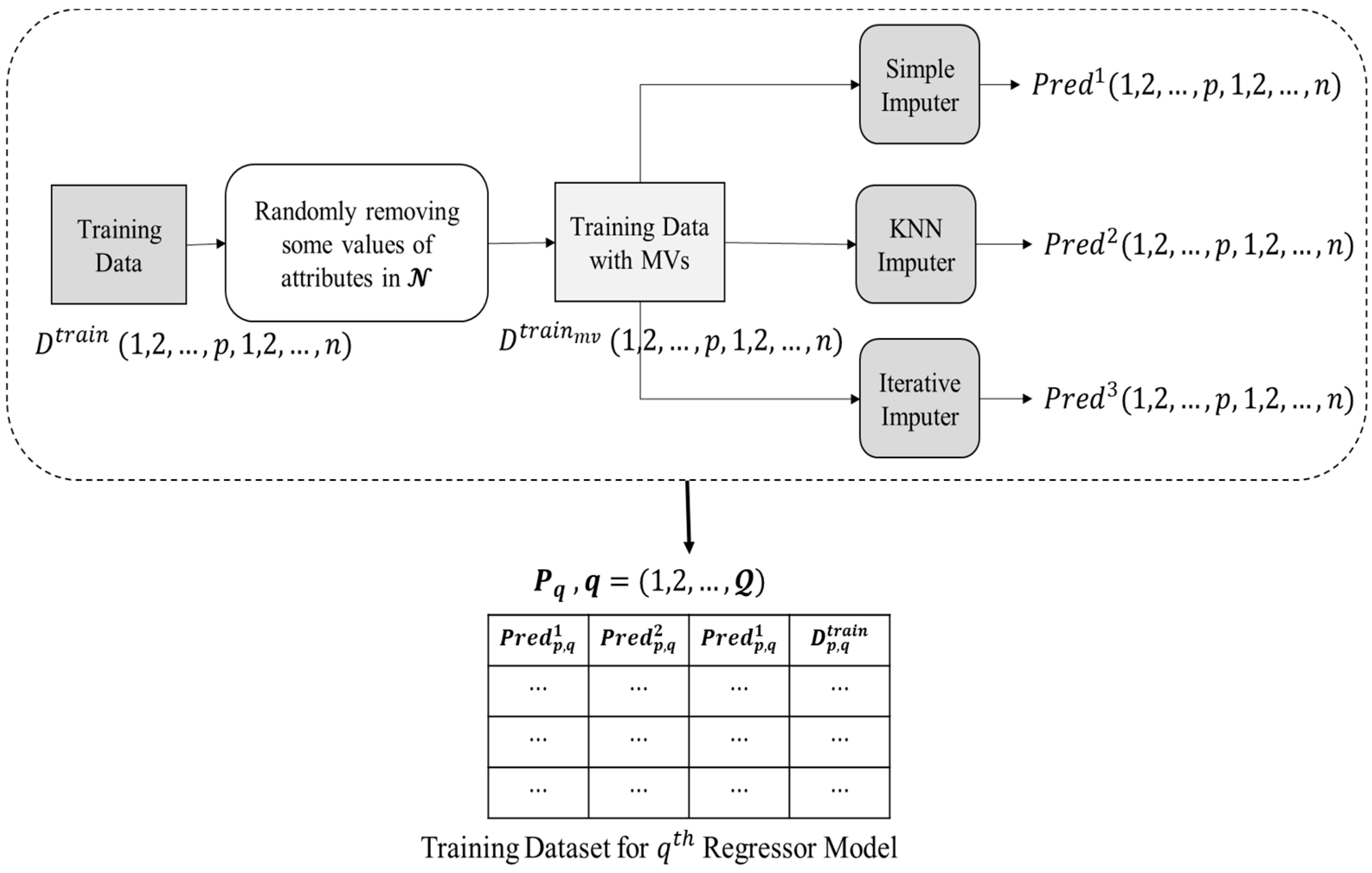
- Initially, the training data i.e., , does not contain any missing values. Thus, a dataset, i.e., , is prepared by randomly eliminating the present values from the features present in .
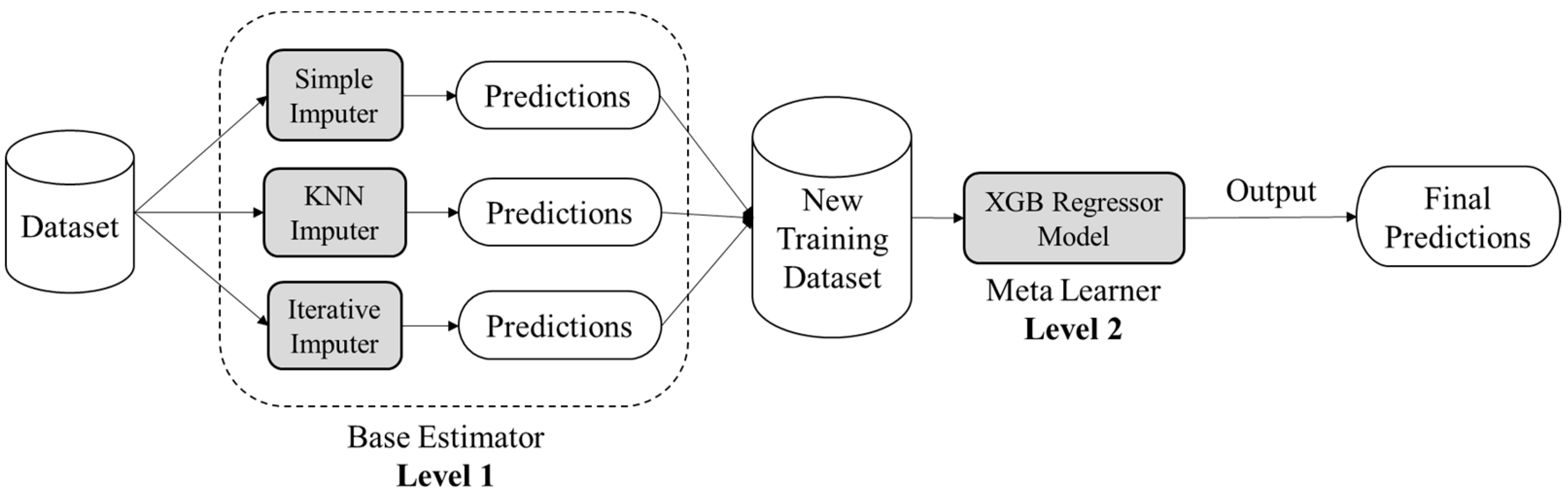
- Three imputation techniques were chosen for the proposed ensemble methodology as unrelated base predictors since using unrelated base predictors may significantly reduce prediction errors in ensemble learning, as indicated in [40]. data is passed to three imputation methods, i.e., (1) simple mean imputer, (2) KNN imputer, and (3) iterative imputer, that have been chosen as base predictors in current research.
- Simple mean imputer: Missing values are substituted in this imputer by the mean of all non-missing values in the corresponding parameter.
- KNN imputer: By assessing respective distance measurements, the KNN method seeks the other k non-missing findings, most comparable to the missing one for every missing value. The missing data is subsequently replaced by a weighted average of the k nearby but non-missing values, with the scores determined by their Euclidean distances from the missing value.
- Iterative imputer: Multiple copies of the same data are generated and then integrated to get the “finest” predicted value in this approach. The MICE technique has been used to provide iterative imputation based on completely conditional requirements.
- The values predicted to be imputed for the missing data in by the base predictors are reserved in three 2-D matrices, i.e., for simple mean, KNN, and iterative imputer, respectively.
- Corresponding to each attribute index in , a regressor model is trained. For training each regressor models, a corresponding matrix (structure presented in Equation (1)) is provided as input.
3.2. Model Training
3.3. Imputation
- In the first section (variable declaration), all the required datasets and matrices have been initialised.
- In the second section, the algorithm performs two sequential tasks.
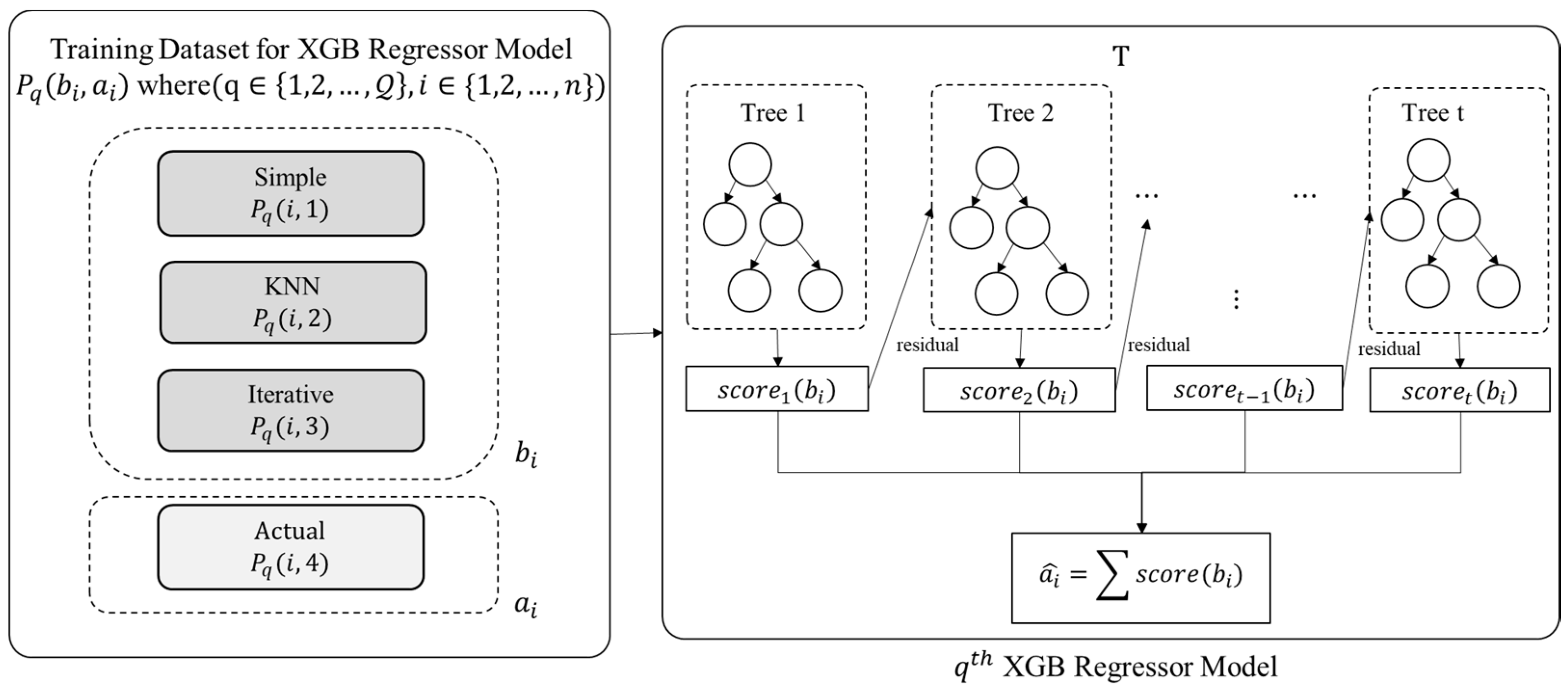
- The first task involves generation of training dataset using three imputation strategies, i.e., simple imputation, kNN imputation, and iterative imputation; after applying imputation method on the training dataset, the resultant dataset is stored in , , and , respectively. Now, for each attribute index present in , a corresponding matrix is formed that comprises of four attributes (simple, kNN, iterative, and actual). The first three attribute elements are represented by vector B denoting the values of qth attribute’s elements imputed by simple imputation, kNN imputation, and iterative imputation method, and the fourth attribute element is represented by vector A, denoting the known value of qth attribute’s elements.
- The second task involves the training of a regressor model (XGB) using generated training dataset. The vectors B and A are passed into XGBRegressor method for training the model and the trained resultant regressor associated with the qth attribute is represented by reg[q].
- In the third section, the algorithm performs three sequential tasks.
- The first task involves the preprocessing of the testing dataset as done in previous section and transform testing dataset representation into matrix associated with each missing valued attribute (q). matrix comprises of three attribute elements represented by vector denoting the values of qth attribute’s elements imputed by simple imputation, kNN imputation, and iterative imputation methods.
Algorithm 1 Proposed Ensemble Model : testing dataset, : dataset with imputed instances
: indexes of attributes having at least one MV.
: dataset with training instances.
: dataset with training instances having randomly assigned MVs.
reg[q]: regressor model associated with qth feature
#Generating training Dataset and training the Model
SimpleImputer(, strategy = ‘mean’)
kNNImputer(, NN = 5)
IterativeImputer(, max_itr = 5)
for qth in :
)
)
reg[q] = XGBRegressor()
reg[q].fit(B,A)
reg[q].predict(B)
#Applying trained ensemble models on
SimpleImputer(, strategy = ‘mean’)
kNNImputer(, NN = 5)
IterativeImputer(, max_itr = 5)
for qth in :
)
= [[q].isna().index]
= reg[q].predict()
for j in [q]:
if [q][j] = nan:
[q][j]= [i++]- b.
- The second task involves the prediction of missing values in testing dataset using trained regressor models (XGB) reg[q] associated with each missing valued attribute (q). The predicted values are stored in a vector
- c.
- Lastly, the third task involves the substitution of imputed results of missing values associated with qth attribute as stored in into the actual dataset . After substitution, the dataset is completed, and no missing value is present in it.
4. Experiments and Results
4.1. Real Time Dataset
4.2. Regressor Models
- eXtreme Gradient Boost Regressor (XGBR): XGBoost is a tree-based enactment of gradient boosting machines (GBM) utilised for supervised machine learning. XGBoost is a widely used machine learning algorithm in Kaggle Competitions [47] and is favoured by data scientists as its high execution speed beats principal computations [37]. The key concept behind boosting regression strategy is the consecutive construction of subsequent trees from a rooted tree such that each successive tree diminishes the errors of the tree previous to it so that the newly formed subsequent trees will update the preceding residuals to decrease the cost function error. In this research, the XGB Regressor Model has a maximum tree depth of 10, and L1 and L2 regularisation terms on weights are set as default, i.e., 0 and 1, respectively.
- Random Forest Regressor (RFR): Random Forest is an ensemble tree-based regression methodology proposed by Leo Breiman. It is a substantial alteration of bootstrap aggregating that builds a huge assemblage of contrasting trees, and after that aggregates them [48]. A random forest predictor comprises an assemblage of unpremeditated regression trees as the base , where , are independent and identically distributed (IID) outcomes of a randomising variable and . An aggregated regression estimate is evaluated by combining all these random trees by using formula , where denotes expectation w.r.t. with the random variable conditionally on A and the dataset . In this research, the maximum depth of RFR tree is tuned to 5, and other parameters, such as the minimum sample split and the number of trees, are kept as the default, i.e., 2 and 1000, respectively.
- Support Vector Regressor (SVR): Support Vector Machine (SVM) used for regression analysis is named as support vector regressor (SVR) [49]. In SVR, the input values are mapped into a higher-dimensional space by some non-linear functions called kernel functions [50,51] so as to make the model linearly separable for making predictions. The SVR model is trained by a structural risk minimisation (SRM) principle [52] to perform regression. This minimises the VC dimension [53] as a replacement for minimising the mean absolute value of error or the squared error. In this research, SVR uses the radial basis function as kernel and a regularisation parameter (C) of 1.5.
4.3. Evaluation Metrics
4.4. Results
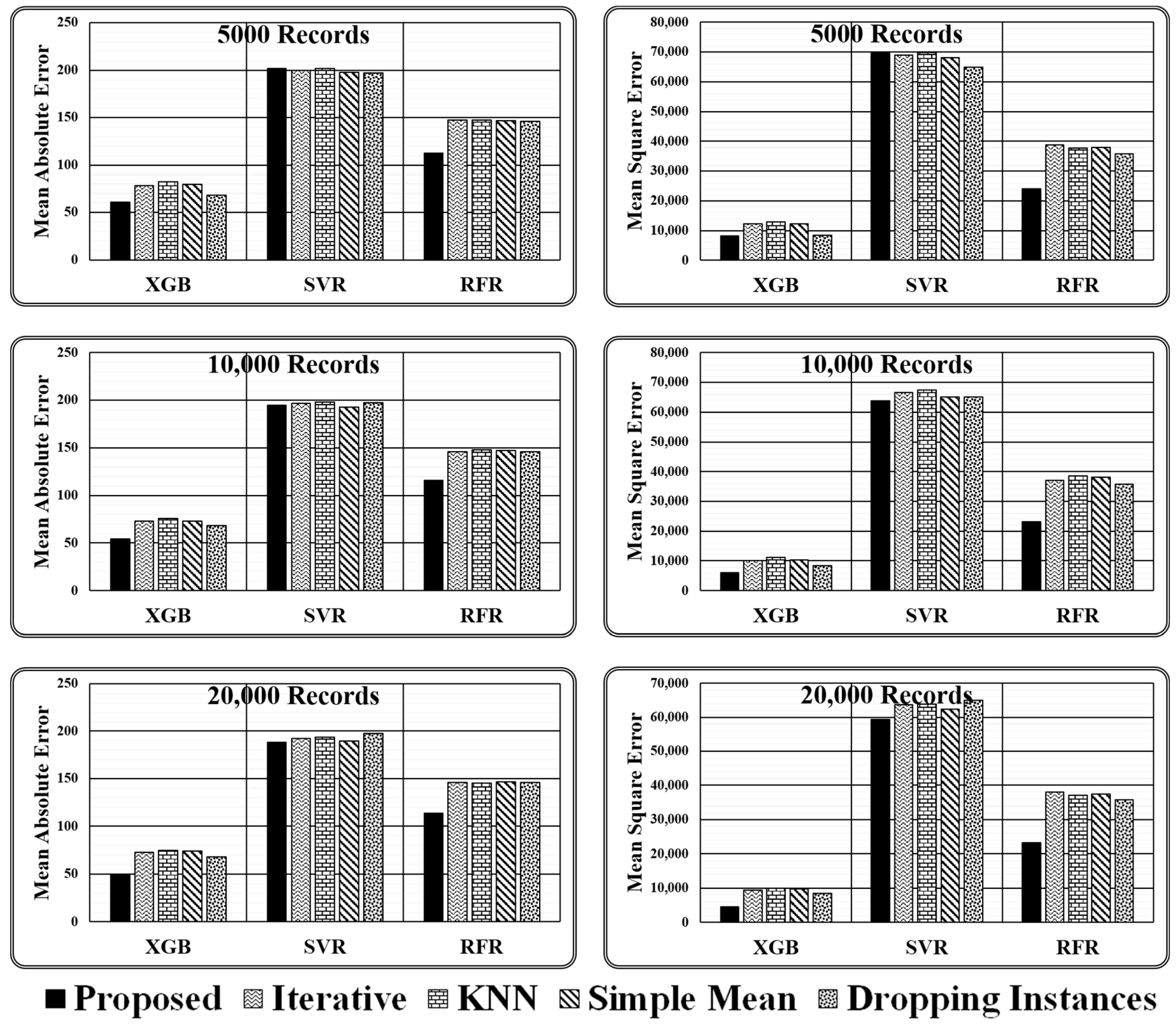
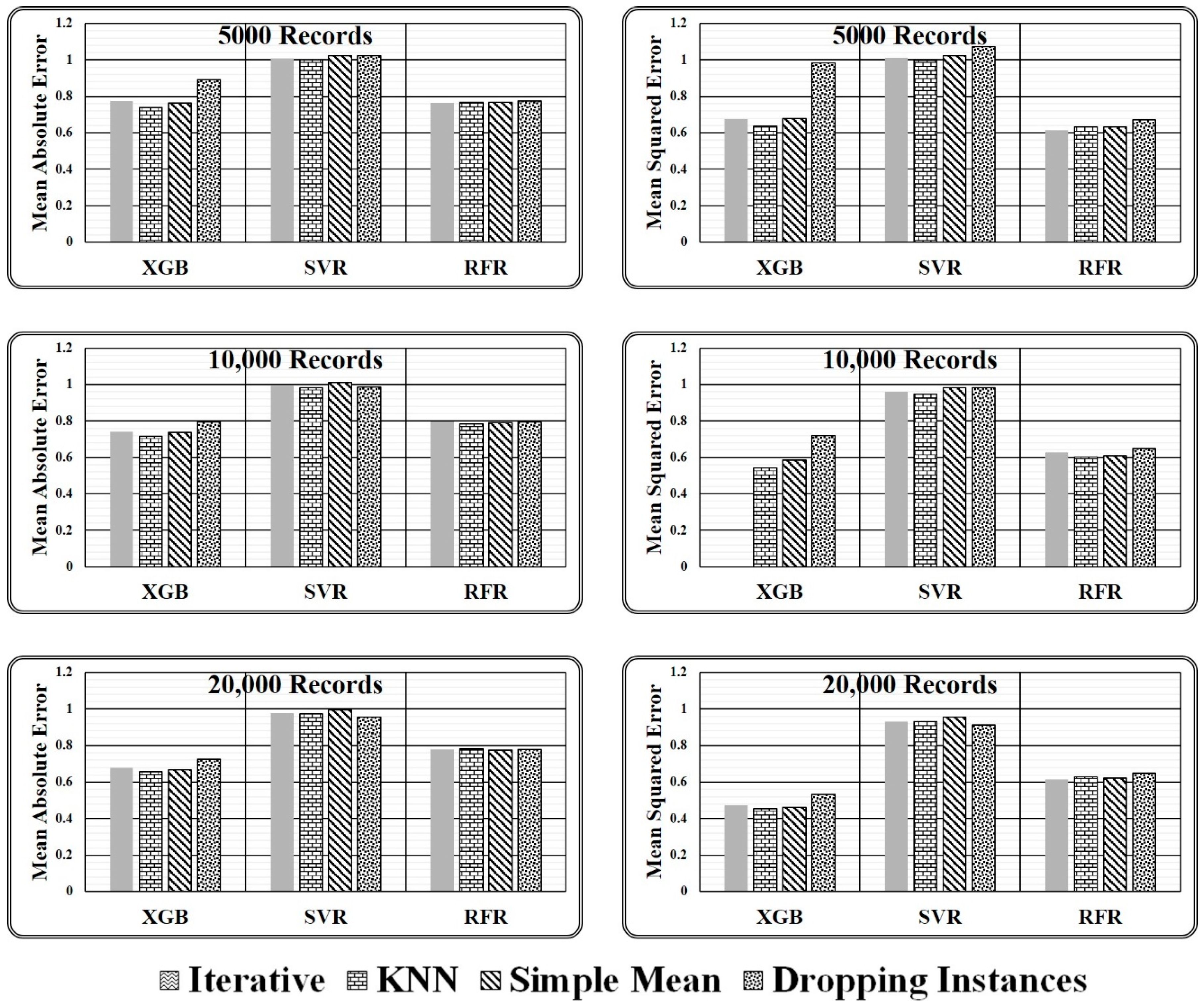
- It has been discovered that primitive imputation strategies, such as iterative, kNN, and simple mean imputation do not perform well when imputing the missing values of huge datasets. When the imputed dataset is submitted to XGB regressor and random forest regressor to assess target values, dropping the records with missing values appears to be highly promising, as demonstrated in Table 5. On the contrary, while making predictions through a support vector regressor, dealing with a large dataset containing comparatively more missing values, dropping the missing values is not recommended. However, when the dataset is small and has fewer missing values, dropping the records holding missing values is the best option, as predicted by all three regression models.
- When working with a small dataset with fewer missing values, all imputation techniques produce similar outcomes when predicted by the SVR Model. On the contrary, in the case of regressor models XGB and RFR, significant variations in the performance of various imputation techniques are observed. The results achieved indicate that the proposed ensemble model outperforms all mentioned primitive imputation techniques when dealing with both large and small datasets by producing the lowest values for mean absolute and mean squared errors. The performance of kNN, iterative, and simple mean imputation to impute missing values individually has been observed to underperform compared to the technique of dropping the records holding missing values. However, the suggested ensemble imputations model outperformed all four scenarios, as validated by the three underlying regression models.
5. Discussion
- Functionally dependent domain: Current research is not exploiting the functional dependencies present in the dataset for identification of missing values. The authors target to employ the devised ensemble strategy on other healthcare datasets including genomics-based and specific disease diagnosis-based, which may include the significance of attribute’s functional dependencies.
- Intelligent selection of base predictors: The base predictors chosen in the proposed model are fixed and thus do not consider other base predictors available. The authors intend to develop a system for intelligent selection and hybridisation of the different base estimators on the basis of attributes, for instance, domain dependency; categorical data must be addressed by classification-based machine learning models and continuous data must be addressed by regression machine learning models. Further, the multiple stacking approach can be integrated for the meta learners in the proposed ensemble approach, wherein the XGB model can be replaced with the kNN-based deep learning methods when handling complex healthcare datasets which can help in producing much better outcomes and can be more reliable in terms of performance.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z. Missing data imputation: Focusing on single imputation. Ann. Transl. Med. 2016, 4, 9. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, A.B.; Mikkelsen, E.M.; Cronin-Fenton, D.; Kristensen, N.R.; Pham, T.M.; Pedersen, L.; Petersen, I. Missing data and multiple imputation in clinical epidemiological research. Clin. Epidemiol. 2017, 9, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Chen, C.; Geng, Q.; Cao, Z.; Chen, X.; Lin, J.; Jin, Y.; Zhang, Z.; Shi, Y.; Zhang, X.D. An Improved Method of Handling Missing Values in the Analysis of Sample Entropy for Continuous Monitoring of Physiological Signals. Entropy 2019, 21, 274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilkinson, M.; Dumontier, M.; Aalbersberg, I.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wong-Lin, K.; McClean, P.L.; McCombe, N.; Kaur, D.; Sanchez-Bornot, J.M.; Gillespie, P.; Todd, S.; Finn, D.P.; Joshi, A.; Kane, J.; et al. Shaping a data-driven era in dementia care pathway through computational neurology approaches. BMC Med. 2020, 18, 398. [Google Scholar] [CrossRef] [PubMed]
- Batra, S.; Sachdeva, S. Pre-Processing Highly Sparse and Frequently Evolving Standardized Electronic Health Records for Mining. In Handbook of Research on Disease Prediction Through Data Analytics and Machine Learning; Rani, G., Tiwari, P., Eds.; IGI Global: Hershey, PA, USA, 2021; pp. 8–21. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112, p. 18. [Google Scholar]
- Mirkes, E.M.; Coats, T.J.; Levesley, J.; Gorban, A.N. Handling missing data in large healthcare dataset: A case study of unknown trauma outcomes. Comput. Biol. Med. 2016, 75, 203–216. [Google Scholar] [CrossRef] [Green Version]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Volume 793. [Google Scholar]
- Sachdeva, S.; Batra, D.; Batra, S. Storage Efficient Implementation of Standardized Electronic Health Records Data. In Proceedings of the 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Seoul, Korea (South), 16–19 December 2020; pp. 2062–2065. [Google Scholar]
- Dong, Y.; Peng, C.Y. Principled missing data methods for researchers. SpringerPlus 2013, 2, 222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farhangfar, A.; Kurgan, L.; Dy, J. Impact of imputation of missing values on classification error for discrete data. Pattern Recogn. 2008, 41, 3692–3705. [Google Scholar] [CrossRef]
- Fichman, M.; Cummings, J.N. Multiple imputation for missing data: Making the most of what you know. Organ. Res. Methods 2003, 6, 282–308. [Google Scholar] [CrossRef]
- Aleryani, A.; Wang, W.; Iglesia, B.D.L. Dealing with missing data and uncertainty in the context of data mining. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Oviedo, Spain, 20–22 June 2018; Springer: Cham, Switzerland, 2018; pp. 289–301. [Google Scholar]
- Frank, E.; Witten, I.H. Generating Accurate Rule Sets without Global Optimization; University of Waikato: Hamilton, New Zealand, 1998. [Google Scholar]
- Efron, B. Missing data, imputation, and the bootstrap. J. Am. Stat. Assoc. 1994, 89, 463–475. [Google Scholar] [CrossRef]
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef] [Green Version]
- Biessmann, F.; Rukat, T.; Schmidt, P.; Naidu, P.; Schelter, S.; Taptunov, A.; Lange, D.; Salinas, D. DataWig: Missing Value Imputation for Tables. J. Mach. Learn. Res. 2019, 20, 1–6. [Google Scholar]
- Beaulieu-Jones, B.K.; Moore, J.H. Pooled Resource Open-Access Als Clinical Trials Consortium. Missing data imputation in the electronic health record using deeply learned autoencoders. In Proceedings of the Pacific Symposium on Biocomputing, Kohala Coast, HI, USA, 3–7 January 2017; Volume 2017, pp. 207–218. [Google Scholar]
- Clavel, J.; Merceron, G.; Escarguel, G. Missing data estimation in morphometrics: How much is too much? Syst. Biol. 2014, 63, 203–218. [Google Scholar] [CrossRef] [PubMed]
- Tada, M.; Suzuki, N.; Okada, Y. Missing Value Imputation Method for Multiclass Matrix Data Based on Closed Itemset. Entropy 2022, 24, 286. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, J.G.; Chu, H.; Chen, M.H. Missing data in clinical studies: Issues and methods. J. Clin. Oncol. 2012, 30, 3297. [Google Scholar] [CrossRef]
- Li, J.; Wang, M.; Steinbach, M.S.; Kumar, V.; Simon, G.J. Don’t do imputation: Dealing with informative missing values in EHR data analysis. In Proceedings of the 2018 IEEE International Conference on Big Knowledge (ICBK), Singapore, 17–18 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 415–422. [Google Scholar]
- Cirugedaroldan, E.; Cuestafrau, D.; Miromartinez, P.; Oltracrespo, S. Comparative Study of Entropy Sensitivity to Missing Biosignal Data. Entropy 2014, 16, 5901–5918. [Google Scholar] [CrossRef]
- Wells, B.J.; Chagin, K.M.; Nowacki, A.S.; Kattan, M.W. Strategies for handling missing data in electronic health record derived data. EGEMS 2013, 1, 1035. [Google Scholar] [CrossRef]
- Pigott, T.D. A review of methods for missing data. Educ. Res. Eval. 2001, 7, 353–383. [Google Scholar] [CrossRef] [Green Version]
- Donders, A.R.T.; Van Der Heijden, G.J.; Stijnen, T.; Moons, K.G. A gentle introduction to imputation of missing values. J. Clin. Epidemiol. 2006, 59, 1087–1091. [Google Scholar] [CrossRef]
- Lankers, M.; Koeter, M.W.; Schippers, G.M. Missing data approaches in eHealth research: Simulation study and a tutorial for nonmathematically inclined researchers. J. Med. Internet Res. 2010, 12, e1448. [Google Scholar]
- Hu, Z.; Melton, G.B.; Arsoniadis, E.G.; Wang, Y.; Kwaan, M.R.; Simon, G.J. Strategies for handling missing clinical data for automated surgical site infection detection from the electronic health record. J. Biomed. Inform. 2017, 68, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Sun, Y.; Zhang, A.; Chen, L.; Wang, J. Enriching data imputation under similarity rule constraints. IEEE Trans. Knowl. Data Eng. 2018, 32, 275–287. [Google Scholar] [CrossRef]
- Nikfalazar, S.; Yeh, C.H.; Bedingfield, S.; Khorshidi, H.A. A new iterative fuzzy clustering algorithm for multiple imputation of missing data. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Song, S.; Sun, Y. Imputing various incomplete attributes via distance likelihood maximization. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Online, 6–10 July 2020; pp. 535–545. [Google Scholar]
- Chu, X.; Ilyas, I.F.; Papotti, P. Holistic data cleaning: Putting violations into context. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 458–469. [Google Scholar]
- Breve, B.; Caruccio, L.; Deufemia, V.; Polese, G. RENUVER: A Missing Value Imputation Algorithm based on Relaxed Functional Dependencies. Open Proceedings. 2022. Available online: https://openproceedings.org/2022/conf/edbt/paper-19.pdf (accessed on 2 April 2022).
- Combi, C.; Mantovani, M.; Sabaini, A.; Sala, P.; Amaddeo, F.; Moretti, U.; Pozzi, G. Mining approximate temporal functional dependencies with pure temporal grouping in clinical databases. Comput. Biol. Med. 2015, 62, 306–324. [Google Scholar] [CrossRef] [PubMed]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13 August 2016. [Google Scholar]
- Turska, E.; Jurga, S.; Piskorski, J. Mood Disorder Detection in Adolescents by Classification Trees, Random Forests and XGBoost in Presence of Missing Data. Entropy 2021, 23, 1210. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2, pp. 1–758. [Google Scholar]
- Troussas, C.; Krouska, A.; Sgouropoulou, C.; Voyiatzis, I. Ensemble Learning Using Fuzzy Weights to Improve Learning Style Identification for Adapted Instructional Routines. Entropy 2020, 22, 735. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, X.; Mu, Y.; Wang, L. Experimental Study and Comparison of Imbalance Ensemble Classifiers with Dynamic Selection Strategy. Entropy 2021, 23, 822. [Google Scholar] [CrossRef]
- Rahimi, N.; Eassa, F.; Elrefaei, L. One- and Two-Phase Software Requirement Classification Using Ensemble Deep Learning. Entropy 2021, 23, 1264. [Google Scholar] [CrossRef]
- Beaulieu-Jones, B.K.; Lavage, D.R.; Snyder, J.W.; Moore, J.H.; Pendergrass, S.A.; Bauer, C.R. Characterizing and managing missing structured data in electronic health records: Data analysis. JMIR Med. Inform. 2018, 6, e8960. [Google Scholar] [CrossRef]
- West, J.; Bhattacharya, M. Intelligent financial fraud detection: A comprehensive review. Comput. Secur. 2016, 57, 47–66. [Google Scholar] [CrossRef]
- Haratian, A.; Fazelinia, H.; Maleki, Z.; Ramazi, P.; Wang, H.; Lewis, M.A.; Greiner, R.; Wishart, D. Dataset of COVID-19 outbreak and potential predictive features in the USA. Data Brief 2021, 38, 107360. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Liu, Q.; Chen, S.; Liu, Y.; Zhang, C.H.; Liu, R. XGBoost-based algorithm interpretation and application on post-fault transient stability status prediction of power system. IEEE Access 2019, 7, 13149–13158. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 28, 779–784. [Google Scholar]
- Wu, M.C.; Lin, G.F.; Lin, H.-Y. Improving the forecasts of extreme streamflow by support vector regression with the data extracted by self-organizing map. Hydrol. Process. 2014, 28, 386–397. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. River stage prediction based on a distributed support vector regression. J. Hydrol. 2008, 358, 96–111. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support Vector Regression for Real-Time Flood Stage Forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Viswanathan, M.; Kotagiri, R. Comparing the performance of support vector machines to regression with structural risk minimisation. In Proceedings of the International Conference on Intelligent Sensing and Information Processing, Chennai, India, 4–7 January 2004. [Google Scholar] [CrossRef]
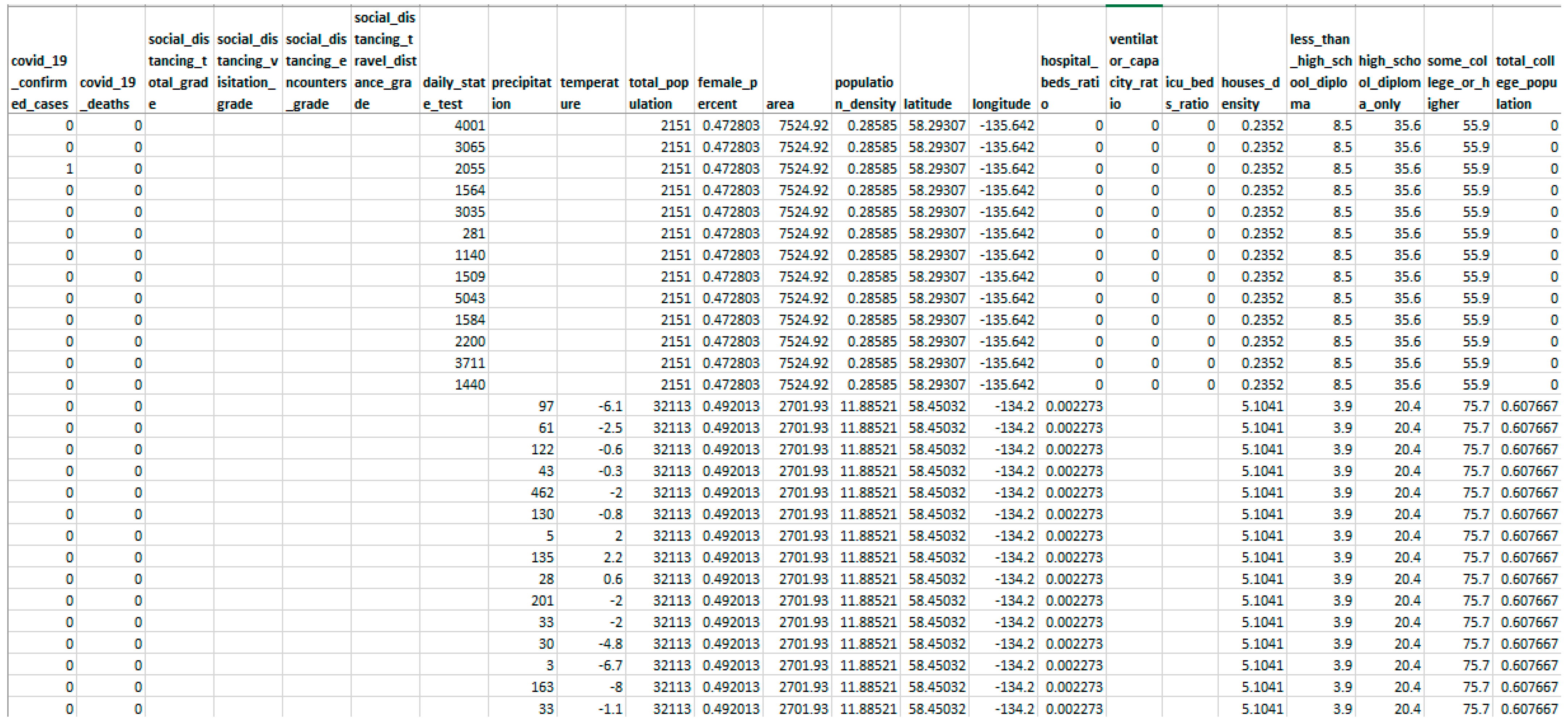

| Regressor/Imputation Methods | Configurations |
|---|---|
| XGB Regressor | max_depth = 10 |
| Support Vector Regressor | Kernel = rbf, C = 1.5 |
| Random Forest | max_depth = 5 |
| K Nearest Neighbour Imputation | K = 5 |
| Multiple Imputation | max_itr = 5 |
| Simple Imputation | strategy = ‘mean’ |
| Proposed Ensemble Model Imputation | NA |
| Test Dataset Size | Number of Instances Holding One or More Missing Values | Frequency of Non-Missing Values | Frequency of Missing Values |
|---|---|---|---|
| 5000 | 3458 | 279,877 | 10,123 |
| 10,000 | 6961 | 559,955 | 20,045 |
| 20,000 | 13,857 | 1,120,278 | 39,722 |
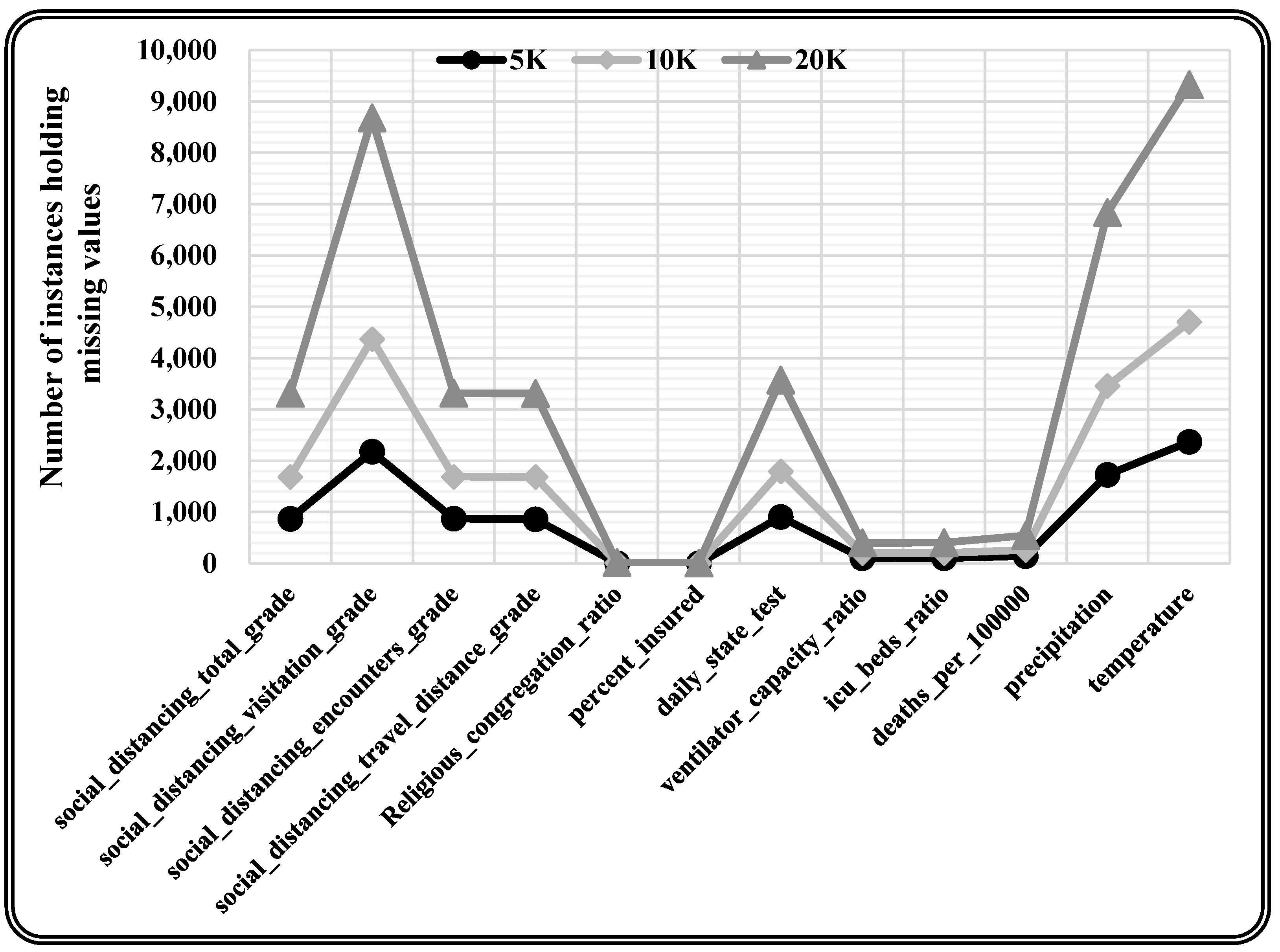
| Attributes Name | 5K Records | 10K Records | 20K Records |
|---|---|---|---|
| social_distancing_total_grade | 868 | 1682 | 3315 |
| social_distancing_visitation_grade | 2176 | 4369 | 8681 |
| social_distancing_encounters_grade | 870 | 1688 | 3315 |
| social_distancing_travel_distance_grade | 860 | 1682 | 3310 |
| daily_state_test | 905 | 1791 | 3572 |
| precipitation | 1727 | 3456 | 6836 |
| temperature | 2368 | 4704 | 9330 |
| ventilator_capacity_ratio | 102 | 201 | 400 |
| icu_beds_ratio | 100 | 200 | 401 |
| Religious_congregation_ratio | 3 | 7 | 13 |
| percent_insured | 1 | 3 | 6 |
| deaths_per_100000 | 143 | 262 | 543 |
| Test Dataset Size | Imputation Method | Mean Absolute Error | Mean Squared Error | ||||
|---|---|---|---|---|---|---|---|
| XGB | SVR | RFR | XGB | SVR | RFR | ||
| 5000 Records | Proposed | 60.81 | 202.01 | 112.8 | 8266.08 | 69,611.7 | 23,966 |
| Iterative | 78.48 | 200.03 | 147.63 | 12,261.7 | 68,882.8 | 38,878.3 | |
| KNN | 82.3 | 201.91 | 147.15 | 12,972.8 | 69,768.5 | 37,811.4 | |
| Simple Mean | 79.78 | 197.48 | 146.88 | 12,197.3 | 68,160.8 | 37,889.9 | |
| Dropping | 68.08 | 197.37 | 145.84 | 8406.14 | 64,981.4 | 35,744.9 | |
| 10,000 Records | Proposed | 54.06 | 194.73 | 115.98 | 6046.26 | 63,853.1 | 23,256.3 |
| Iterative | 72.84 | 196.45 | 145.58 | 10194 | 66,607.9 | 37,104.7 | |
| KNN | 75.58 | 198.2 | 148.12 | 11,154 | 67,537.5 | 38,554.6 | |
| Simple Mean | 73.36 | 192.69 | 146.96 | 10,372.3 | 65,122.9 | 38,134.9 | |
| Dropping | 68.08 | 197.37 | 146 | 8406.14 | 64,981.4 | 35,805.3 | |
| 20,000 Records | Proposed | 49.38 | 188.31 | 113.57 | 4473.7 | 59,422.4 | 23,298.4 |
| Iterative | 72.69 | 192.51 | 145.98 | 9462.76 | 63,737.1 | 37,942.4 | |
| KNN | 75.01 | 193.38 | 145.21 | 9881.5 | 63,836.4 | 37,135.2 | |
| Simple Mean | 74.07 | 189.46 | 146.65 | 9695.8 | 62,288.6 | 37,528.1 | |
| Dropping | 68.08 | 197.37 | 146.02 | 8406.14 | 64,981.4 | 35,825.6 | |
| Test Dataset Size | Imputation Method | Mean Absolute Error | Mean Squared Error | ||||
|---|---|---|---|---|---|---|---|
| XGB | SVR | RFR | XGB | SVR | RFR | ||
| 5000 Records | Iterative | 0.775 | 1.010 | 0.764 | 0.674 | 1.011 | 0.616 |
| KNN | 0.739 | 1 | 0.767 | 0.637 | 0.998 | 0.634 | |
| Simple Mean | 0.762 | 1.023 | 0.768 | 0.678 | 1.021 | 0.633 | |
| Dropping | 0.893 | 1.024 | 0.773 | 0.983 | 1.071 | 0.67 | |
| 10,000 Records | Iterative | 0.742 | 0.991 | 0.797 | 0.593 | 0.959 | 0.627 |
| KNN | 0.715 | 0.982 | 0.783 | 0.542 | 0.945 | 0.603 | |
| Simple Mean | 0.737 | 1.011 | 0.789 | 0.583 | 0.981 | 0.610 | |
| Dropping | 0.794 | 0.987 | 0.794 | 0.719 | 0.983 | 0.650 | |
| 20,000 Records | Iterative | 0.679 | 0.978 | 0.778 | 0.473 | 0.932 | 0.614 |
| KNN | 0.658 | 0.974 | 0.782 | 0.453 | 0.931 | 0.627 | |
| Simple Mean | 0.667 | 0.994 | 0.774 | 0.461 | 0.954 | 0.621 | |
| Dropping | 0.725 | 0.954 | 0.778 | 0.532 | 0.914 | 0.650 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batra, S.; Khurana, R.; Khan, M.Z.; Boulila, W.; Koubaa, A.; Srivastava, P. A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records. Entropy 2022, 24, 533. https://doi.org/10.3390/e24040533
Batra S, Khurana R, Khan MZ, Boulila W, Koubaa A, Srivastava P. A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records. Entropy. 2022; 24(4):533. https://doi.org/10.3390/e24040533
Chicago/Turabian StyleBatra, Shivani, Rohan Khurana, Mohammad Zubair Khan, Wadii Boulila, Anis Koubaa, and Prakash Srivastava. 2022. "A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records" Entropy 24, no. 4: 533. https://doi.org/10.3390/e24040533
APA StyleBatra, S., Khurana, R., Khan, M. Z., Boulila, W., Koubaa, A., & Srivastava, P. (2022). A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records. Entropy, 24(4), 533. https://doi.org/10.3390/e24040533









