Preference-Tree-Based Real-Time Recommendation System
Abstract
:1. Introduction
- A time-variant recommendation system is proposed. The proposed system generates preference trees based on a user’s history, which are then used to create a collaborative similar graph (CSG). The CSG is then used to define similarity groups to solve the data sparsity problem for users with insufficient historical data.
- Generalized preferences are considered by creating a federated tree for the entire user history to solve the cold-start and data-sparsity problems.
2. Related Work
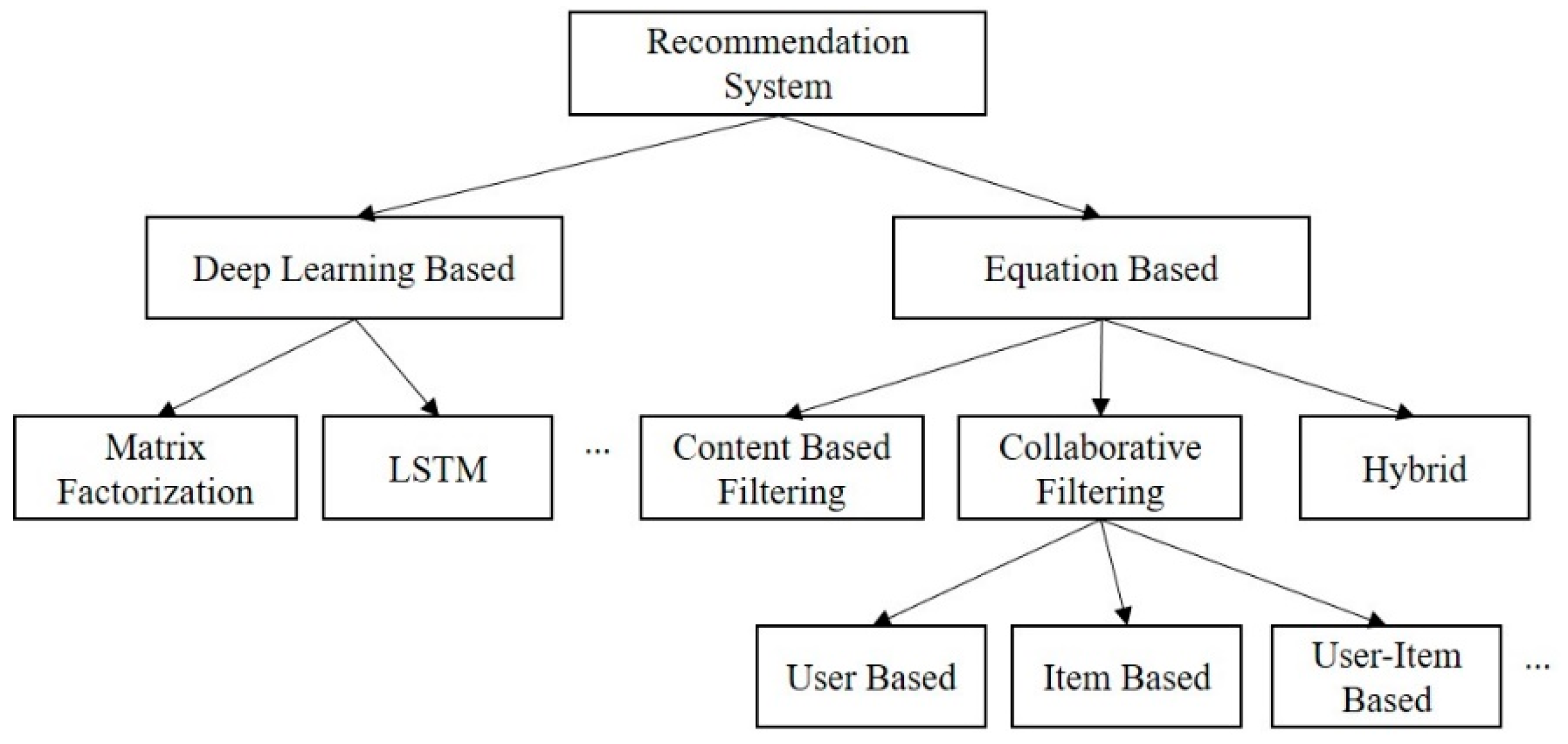
2.1. Recommendation Systems
2.2. Recommendation in Real-Time Systems
3. Proposed System
3.1. Proposed Recommendation System
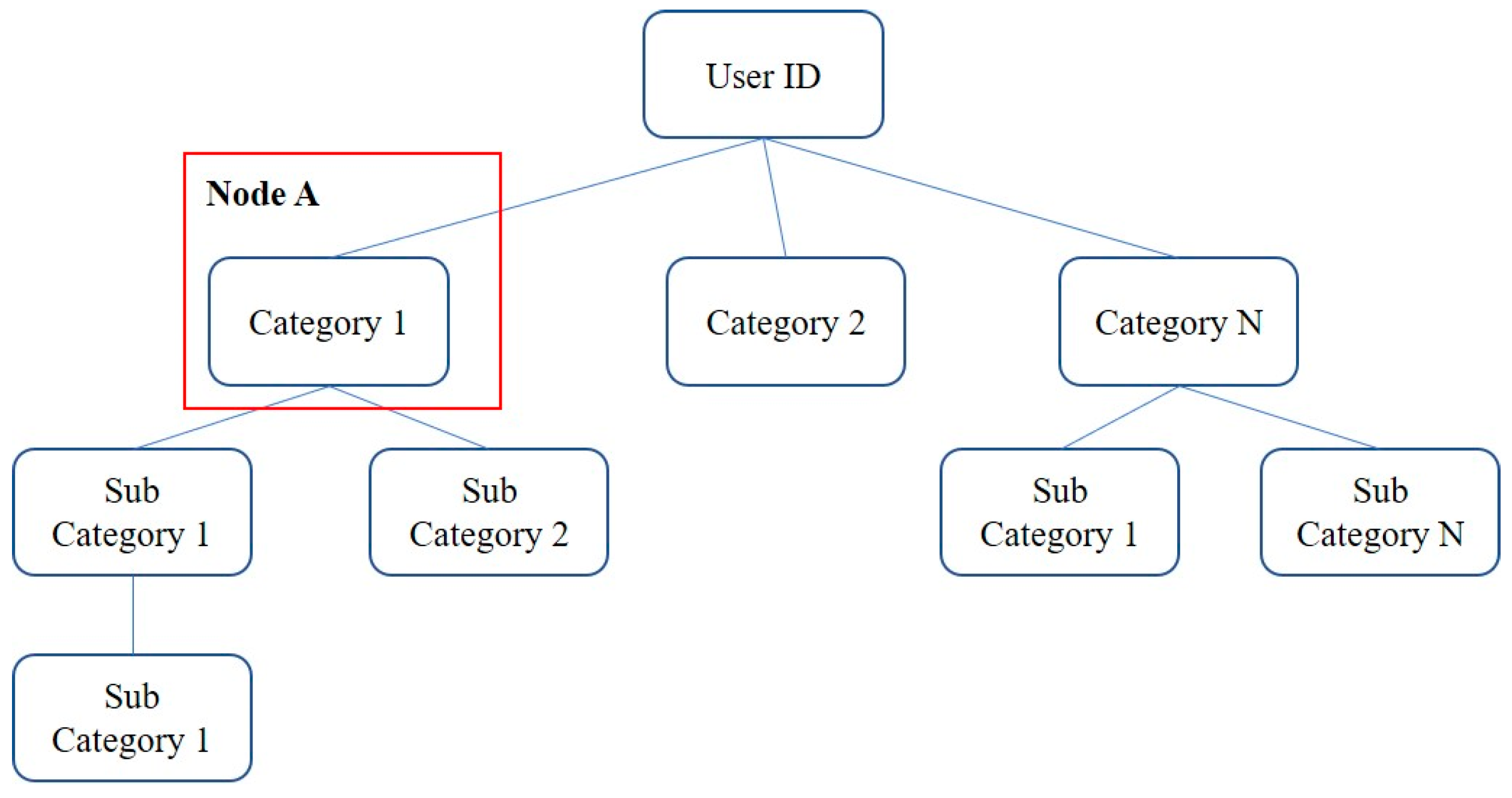
3.2. Preference Tree Model
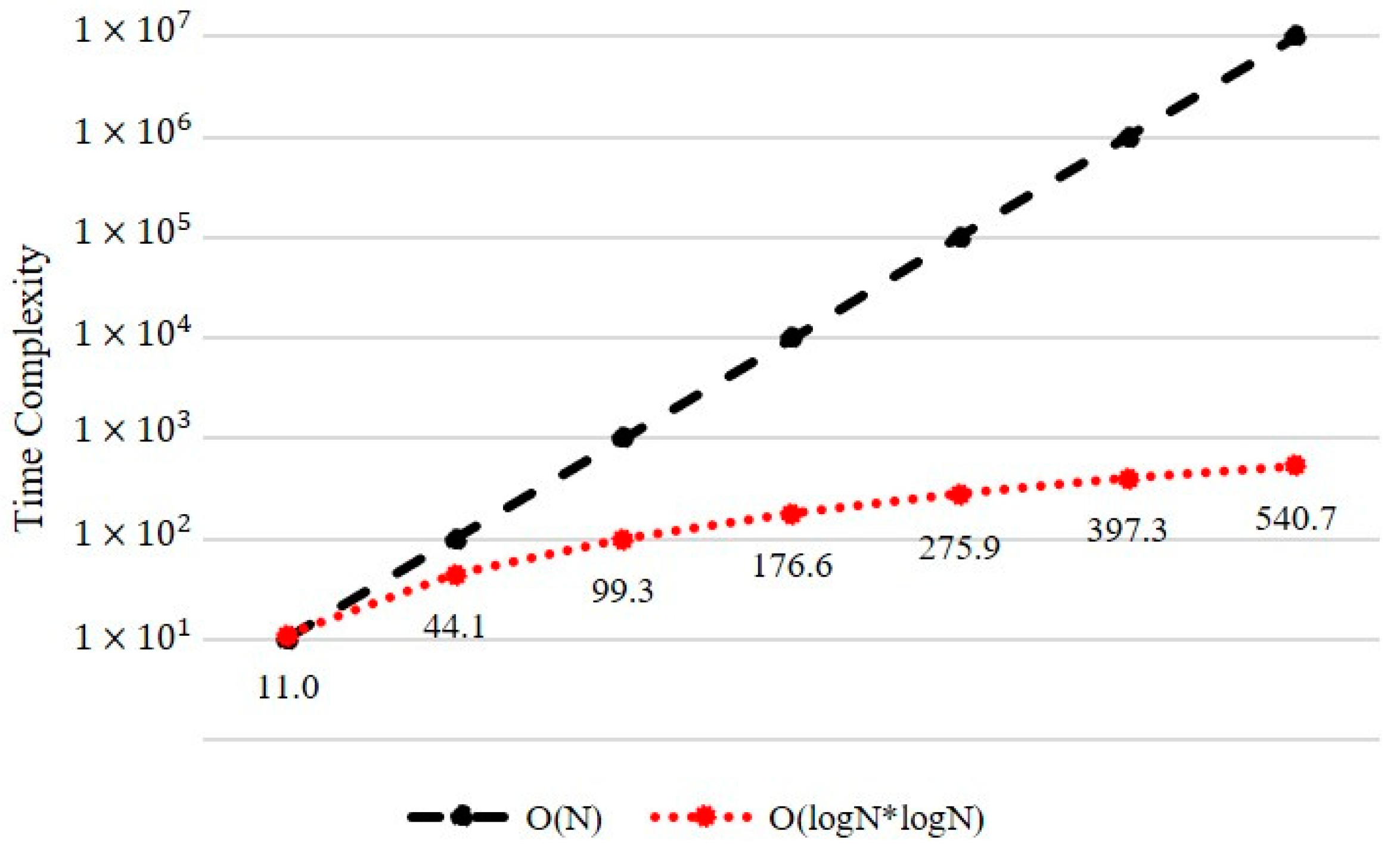
3.3. Tree Model Formulation
3.4. Federated Tree
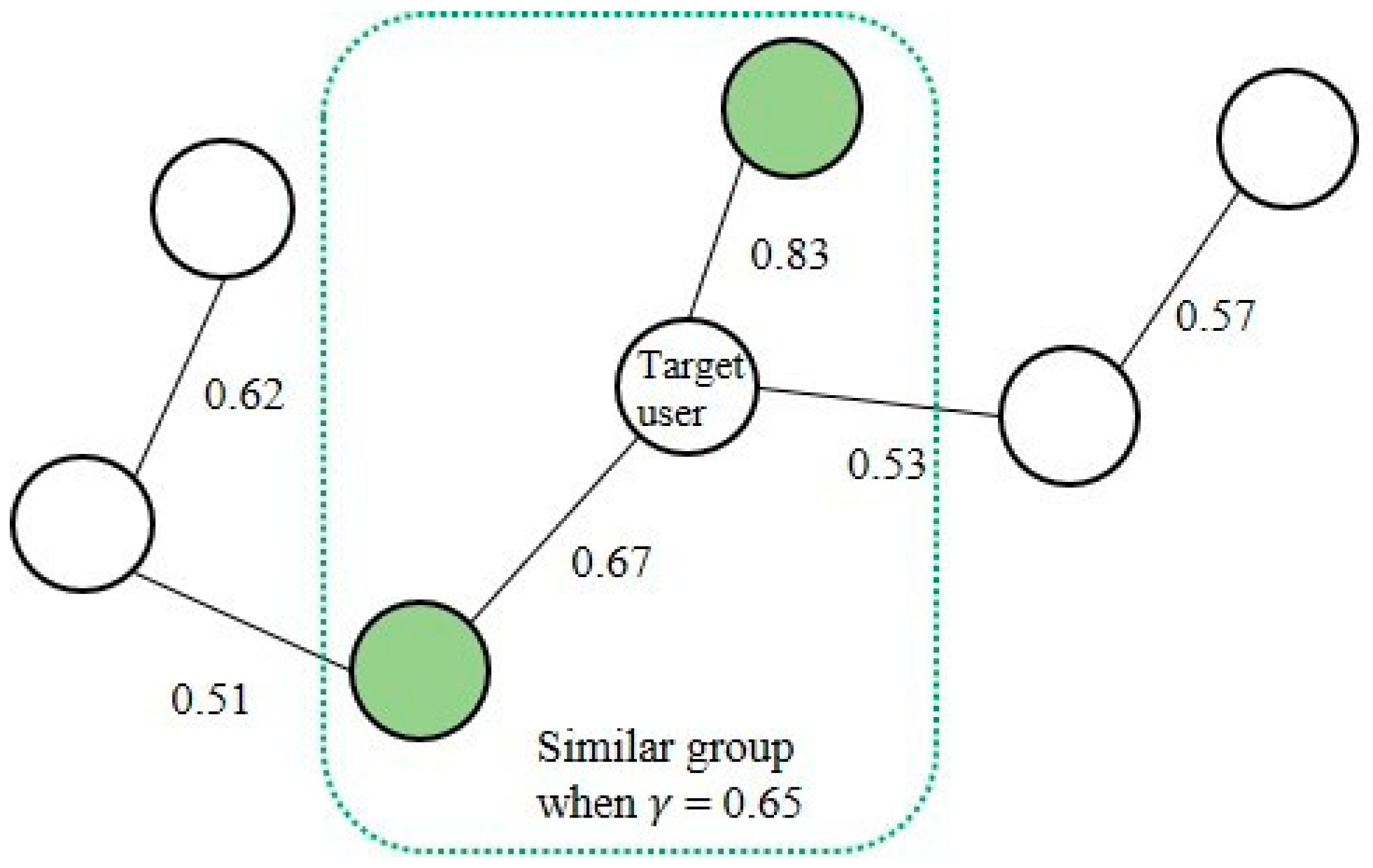
3.5. Similarity Tree
| Algorithm 1. Computing similarity between users A and B | |
| Input: | |
| Output: | |
| 1: | Initialize to 0 |
| 2: | procedure) do |
| 3: | let S be a stack |
| 4: | for all |
| 5: | S.push(node) |
| 6: | while S is not empty do |
| 7: | S.pop() |
| 8: | find in |
| 9: | if is exist |
| 10: | |
| 11: | return |
3.6. Recommendation Algorithm
4. Experimental Evaluation
4.1. Dataset
4.2. Evaluation Metrics
4.3. Experimental Environment
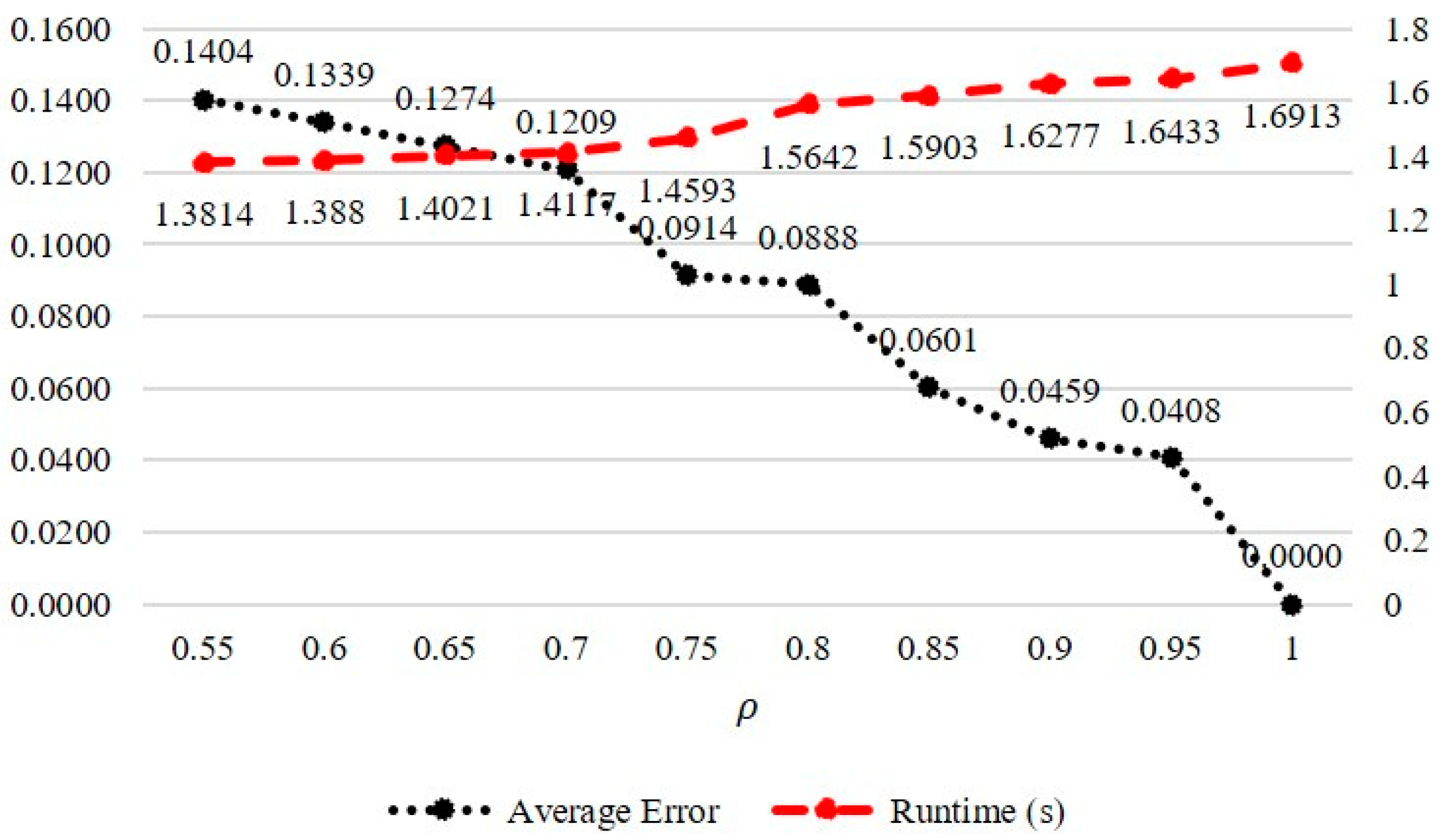
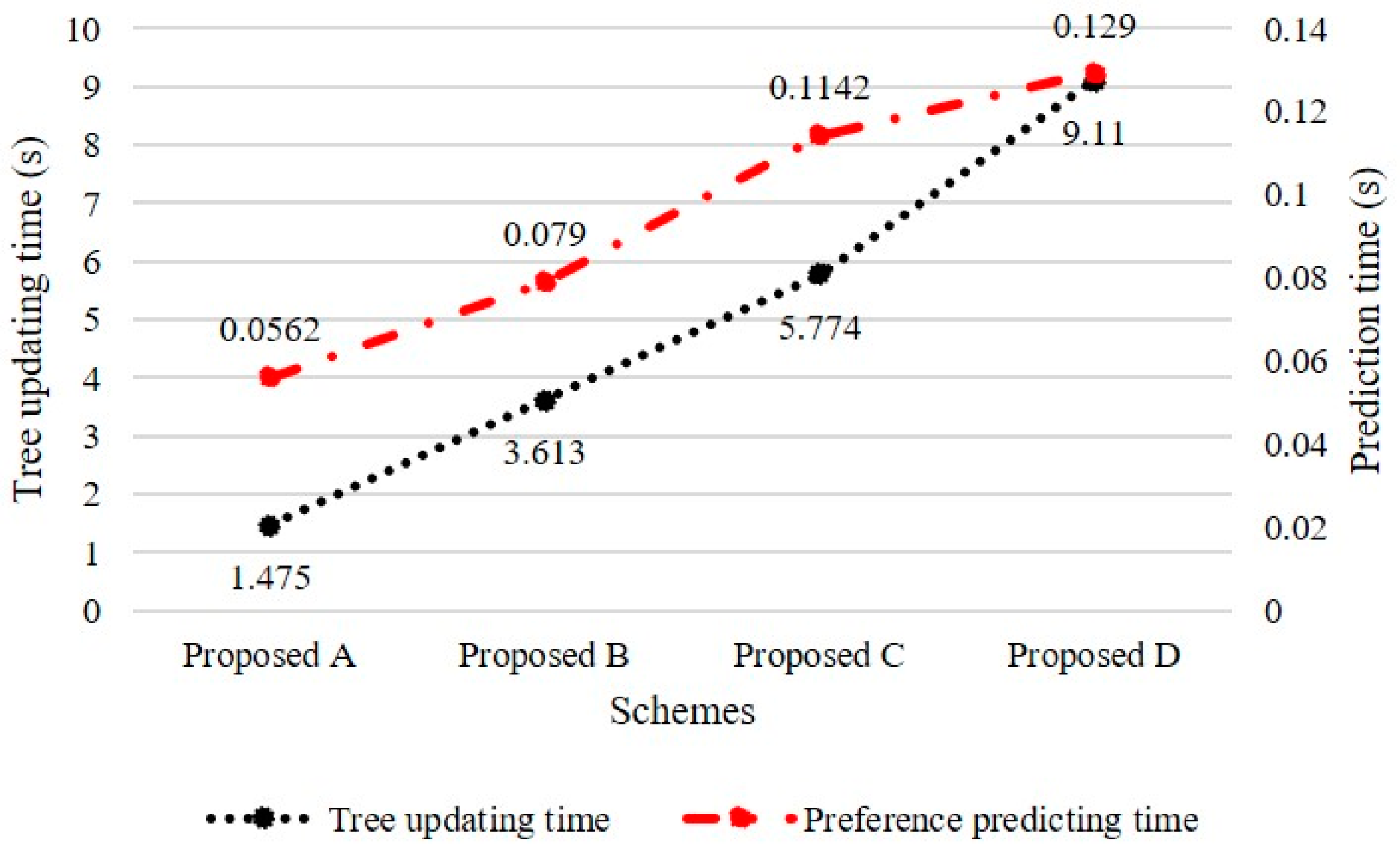
4.4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, C.; Shi, L.; Sun, R.; Wang, J. Improved collaborative filtering recommendation algorithm based on differential privacy protection. J. Supercomput. 2020, 76, 253–258. [Google Scholar] [CrossRef]
- Bradley, K.; Smyth, B. Improving Recommendation Diversity. In Proceedings of the Twelfth Irish Conference on Artificial Intelligence and Cognitive Science, Maynooth, Ireland, 29 May 2022. [Google Scholar]
- Mcfee, B.; Barrington, L.; Lanckeriet, G. Learning content similarity for music recommendation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2207–2218. [Google Scholar] [CrossRef]
- Yang, B.; Mei, T.; Hua, X.-S.; Yang, L.; Yang, S.-Q.; Li, M. Online Video Recommendation Based on Multimodal Fusion and Relevance Feedback. In Proceedings of the 6th ACM International Conference on Image and Video Retrieval, Amsterdam, The Netherlands, 9–11 July 2007. [Google Scholar]
- Mei, T.; Yang, B.; Hua, X.-S.; Yang, L.; Yang, S.-Q.; Li, S. Videoreach: An Online Video Recommendation System. In Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Amsterdam, The Netherlands, 23–27 July 2007. [Google Scholar]
- Yin, H.; Wang, Q.; Zheng, K.; Li, Z.; Zhou, X. Overcoming data sparsity in group recommendation. IEEE Trans. Knowl. Data Eng. 2020, 210–219. [Google Scholar] [CrossRef]
- Kumar, P.; Ramjeevan, S.T. Recommendation system techniques and related issues: A survey. Inter. J. Inf. Technol. 2018, 10, 495–501. [Google Scholar] [CrossRef]
- Hu, Y.; Qimin, P.; Xiaohui, H. A Time-Aware and Data Sparsity Tolerant Approach for Web Service Recommendation. In Proceedings of the 2014 IEEE International Conference on Web Services, Anchorage, AK, USA, 27 June–2 July 2014. [Google Scholar]
- Schafer, J.B.; Frankowski, D.; Herlocker, J.; Sen, S. Collaborative Filtering Recommender Systems; The Adaptive Web. Lecture Notes in Computer Science; Brusilovsky, P., Kobsa, A., Nejdl, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4321, pp. 291–324. [Google Scholar]
- Chi, Y.; Yue, M.L.; Yuxin, C. Nonconvex optimization meets low-rank matrix factorization: An overview. IEEE Trans. Signal Process. 2019, 67, 5239–5269. [Google Scholar] [CrossRef] [Green Version]
- Bobadilla, J.; Ortega, F.; Hernando, F.; Gutiérrez, A. Recommender systems survey. Knowl. Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Mohamed, H.K.; Mohamed, H.I. Recommender Systems Challenges and Solutions Survey. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019. [Google Scholar]
- Reddy, S.R.S.; Nalluri, S.; Kunisetti, S.; Ashok, S.; Venkatesh, B. Content-based movie recommendation system using genre correlation. In Smart Intelligent Computing and Applications; Suresh, C., Vikrant, B.D., Eds.; Springer: Singapore, 2019; pp. 391–397. [Google Scholar]
- Wang, D.; Liang, Y.; Xu, D.; Feng, X.; Guan, R. A content-based recommender system for computer science publications. Knowl. Based Syst. 2018, 157, 1–9. [Google Scholar] [CrossRef]
- Badriyah, T.; Azvy, S.; Yuwono, W.; Syarif, I. Recommendation System for Property Search Using Content based Filtering Method. In Proceedings of the 2018 International Conference on Information and Communications Technology (ICOIACT), Bandung, Indonesia, 2 August 2022. [Google Scholar]
- Zhu, Z.; Liang, J.; Li, D.; Yu, H.; Liu, G. Hot topic detection based on a refined TF-IDF algorithm. IEEE Access 2019, 7, 26996–27007. [Google Scholar] [CrossRef]
- Ben-Porat, O.; Moshe, T. A game-theoretic approach to recommendation systems with strategic content providers. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Nilashi, M.; Othman, I.; Karamollah, B. A recommender system based on collaborative filtering using ontology and dimensionality reduction techniques. Expert Syst. Appl. 2018, 92, 507–520. [Google Scholar] [CrossRef]
- Koohi, H.; Kourosh, K. A new method to find neighbor users that improves the performance of collaborative filtering. Expert Syst. Appl. 2017, 83, 30–39. [Google Scholar] [CrossRef]
- Xue, F.; He, X.; Wang, X.; Xu, J.; Liu, K.; Hong, R. Deep item-based collaborative filtering for top-n recommendation. ACM Trans. Info. Syst. (TOIS) 2019, 37, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Koohi, H.; Kourosh, K. User based collaborative filtering using fuzzy C-means. Measurement 2016, 91, 134–139. [Google Scholar] [CrossRef]
- Tan, Z.; Liangliang, H. An efficient similarity measure for user-based collaborative filtering recommender systems inspired by the physical resonance principle. IEEE Access 2017, 5, 27211–27228. [Google Scholar] [CrossRef]
- Ar, Y.; Erkan, B. A genetic algorithm solution to the collaborative filtering problem. Expert Syst. Appl. 2016, 61, 122–128. [Google Scholar] [CrossRef]
- Al Hassanieh, L.; Jaoudeh, C.A.; Abdo, J.B.; Demerjian, J. Similarity Measures for Collaborative Filtering Recommender Systems. In Proceedings of the 2018 IEEE Middle East and North Africa Communications Conference (MENACOMM), Jounieh, Lebanon, 18–20 April 2018. [Google Scholar]
- Park, Y.; Jinoh, O.; Hwanjo, Y. RecTime: Real-time recommender system for online broadcasting. Inf. Sci. 2017, 409, 1–16. [Google Scholar] [CrossRef]
- Xu, M.; Shenghao, L. Semantic-enhanced and context-aware hybrid collaborative filtering for event recommendation in event-based social networks. IEEE Access 2019, 7, 17493–17502. [Google Scholar] [CrossRef]
- Wei, J.; He, J.; Chen, K.; Zhou, Y.; Tang, Z. Collaborative filtering and deep learning based recommendation system for cold start items. Expert Syst. Appl. 2017, 69, 29–39. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep learning based recommender system: A survey and new perspectives. ACM Comput. Surveys (CSUR) 2019, 52, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Hong, D.; Li, Y.; Jing, P. Low-rank regularized deep collaborative matrix factorization for micro-video multi-label classification. IEEE Signal Process. Lett. 2020, 27, 740–744. [Google Scholar] [CrossRef]
- Yi, B. Deep matrix factorization with implicit feedback embedding for recommendation system. IEEE Trans. Ind. Informat. 2019, 15, 4591–4601. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Zhao, S.; Qian, F.; Zhang, Y. Deep attention user-based collaborative filtering for recommendation. Neurocomputing 2020, 383, 57–68. [Google Scholar] [CrossRef]
- Fu, M.; Qu, H.; Yi, Z.; Lu, L.; Liu, Y. A novel deep learning-based collaborative filtering model for recommendation system. IEEE Trans. Cybern. 2018, 49, 1084–1096. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, H.; Huang, Z.; Du, X.; Yang, G.; Lian, D. Discrete Deep Learning for Fast Content-Aware Recommendation. In Proceedings of the Eleventh ACM International Conference on Web Search and DATA mining, Marina Del Rey, CA, USA, 5–9 February 2018. [Google Scholar]
- He, X.; Zhang, H.; Kan, M.-Y.; Chua, T.-S. Fast matrix factorization for Online Recommendation with Implicit Feedback. In Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval, Pisa, Italy, 17–21 July 2016. [Google Scholar]
- Li, H.; Diao, X.; Cao, J.; Zheng, Q. Collaborative filtering recommendation based on all-weighted matrix factorization and fast optimization. IEEE Access 2018, 6, 25248–25260. [Google Scholar] [CrossRef]
- Chen, L.; Guoxin, Z.; Eric, Z. Fast greedy map inference for determinantal point process to improve recommendation diversity. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Zhu, H.; Li, X.; Zhang, P.; Li, G.; He, J.; Li, H.; Gai, K. Learning Tree-Based Deep Model for Recommender Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2018. [Google Scholar]
- Mu, Y.; Xiaodong, L.; Lidong, W. A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf. Sci. 2018, 435, 40–58. [Google Scholar] [CrossRef]
- Rathore, S.S.; Sandeep, K. A decision tree logic based recommendation system to select software fault prediction techniques. Computing 2017, 99, 255–285. [Google Scholar] [CrossRef]
- Kang, S.; Jeong, C.; Chung, K. Tree-based real-time advertisement recommendation system in online broadcasting. IEEE Access 2020, 8, 192693–192702. [Google Scholar] [CrossRef]
- He, R.; Julian, M. Ups and Downs: Modeling the Visual Evolution of Fashion Trends with One-Class Collaborative Filtering. In Proceedings of the 25th International Conference on World Wide Web, Montréal, QC, Canada, 11–15 April 2016. [Google Scholar]
- McAuley, J.; Targett, C.; Shi, Q.; van den Hengel, A. Image-Based Recommendations on Styles and Substitutes. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago, Chile, 9–13 August 2015. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Tech. 2011, 2, 37–63. [Google Scholar]
- Noy, N.F.; Sintek, M.; Decker, S.; Crubezy, M.; Fergerson, R.W. Creating semantic web contents with protege-2000. IEEE Intell. Syst. 2001, 16, 60–71. [Google Scholar] [CrossRef]
- McBride, B. Jena: A semantic web toolkit. IEEE Internet Comput. 2002, 6, 55–59. [Google Scholar] [CrossRef]

| Component | Description |
|---|---|
| Mapped category code of the node | |
| Number of category cs in user’s historical data | |
| Child nodes of the category c node | |
| Depth of the category c node | |
| Total number of categories at depth d | |
| Maximum depth of the descendant node | |
| User preference for the category c node | |
| Weight of historical data in the ith section |
| Precision | Recall | F1-Measure | Accuracy | Novelty | |
|---|---|---|---|---|---|
| 0.3 | 0.659 | 0.713 | 0.685 | 0.596 | 0.285 |
| 0.4 | 0.633 | 0.737 | 0.681 | 0.579 | 0.224 |
| 0.5 | 0.646 | 0.725 | 0.683 | 0.588 | 0.302 |
| 0.6 | 0.635 | 0.739 | 0.683 | 0.570 | 0.331 |
| 0.7 | 0.620 | 0.739 | 0.674 | 0.571 | 0.275 |
| 0.8 | 0.604 | 0.689 | 0.644 | 0.543 | 0.292 |
| Precision | Recall | F1-Measure | Accuracy | Novelty | |
|---|---|---|---|---|---|
| 0.4 | 0.584 | 0.661 | 0.620 | 0.545 | 0.329 |
| 0.5 | 0.601 | 0.685 | 0.641 | 0.578 | 0.302 |
| 0.6 | 0.612 | 0.747 | 0.673 | 0.582 | 0.285 |
| 0.7 | 0.619 | 0.751 | 0.678 | 0.589 | 0.224 |
| Precision | Recall | F1-Measure | Accuracy | Novelty | |
|---|---|---|---|---|---|
| 0.3 | 0.572 | 0.739 | 0.645 | 0.550 | 0.234 |
| 0.4 | 0.598 | 0.742 | 0.662 | 0.556 | 0.299 |
| 0.5 | 0.601 | 0.685 | 0.641 | 0.578 | 0.372 |
| 0.6 | 0.606 | 0.709 | 0.653 | 0.588 | 0.385 |
| 0.7 | 0.601 | 0.699 | 0.647 | 0.572 | 0.424 |
| 0.8 | 0.625 | 0.656 | 0.640 | 0.559 | 0.422 |
| Scheme | Precision | Recall | F1-Measure | Accuracy | Novelty |
|---|---|---|---|---|---|
| Proposed Scheme A | 0.581 | 0.704 | 0.637 | 0.513 | 0.188 |
| Proposed Scheme B | 0.554 | 0.759 | 0.640 | 0.588 | 0.341 |
| Proposed Scheme C | 0.583 | 0.722 | 0.645 | 0.529 | 0.332 |
| Proposed Scheme D | 0.606 | 0.709 | 0.653 | 0.588 | 0.385 |
| MF-based | 0.590 | 0.682 | 0.633 | 0.544 | 0.229 |
| Max-heap-tree-based | 0.553 | 0.611 | 0.581 | 0.467 | 0.113 |
| Knowledge-based | 0.718 | 0.633 | 0.673 | 0.575 | NAN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.; Chung, K. Preference-Tree-Based Real-Time Recommendation System. Entropy 2022, 24, 503. https://doi.org/10.3390/e24040503
Kang S, Chung K. Preference-Tree-Based Real-Time Recommendation System. Entropy. 2022; 24(4):503. https://doi.org/10.3390/e24040503
Chicago/Turabian StyleKang, Seongju, and Kwangsue Chung. 2022. "Preference-Tree-Based Real-Time Recommendation System" Entropy 24, no. 4: 503. https://doi.org/10.3390/e24040503
APA StyleKang, S., & Chung, K. (2022). Preference-Tree-Based Real-Time Recommendation System. Entropy, 24(4), 503. https://doi.org/10.3390/e24040503






