Quasi-Consensus of Time-Varying Multi-Agent Systems with External Inputs under Deception Attacks
Abstract
:1. Introduction
- (1)
- Compared with the traditional assumption on the time-varying system matrix of MASs, more general and practical conditions are considered in this paper versus the analysis approaches used in [5].
- (2)
- Both false data injection attacks modeled with Bernoulli variables and external inputs are considered in this paper. Moreover, sufficient conditions for achieving the quasi-consensus are derived, and the error upper bounds related to the external inputs and deception attacks are also obtained.
2. Preliminaries
2.1. Graph Theory
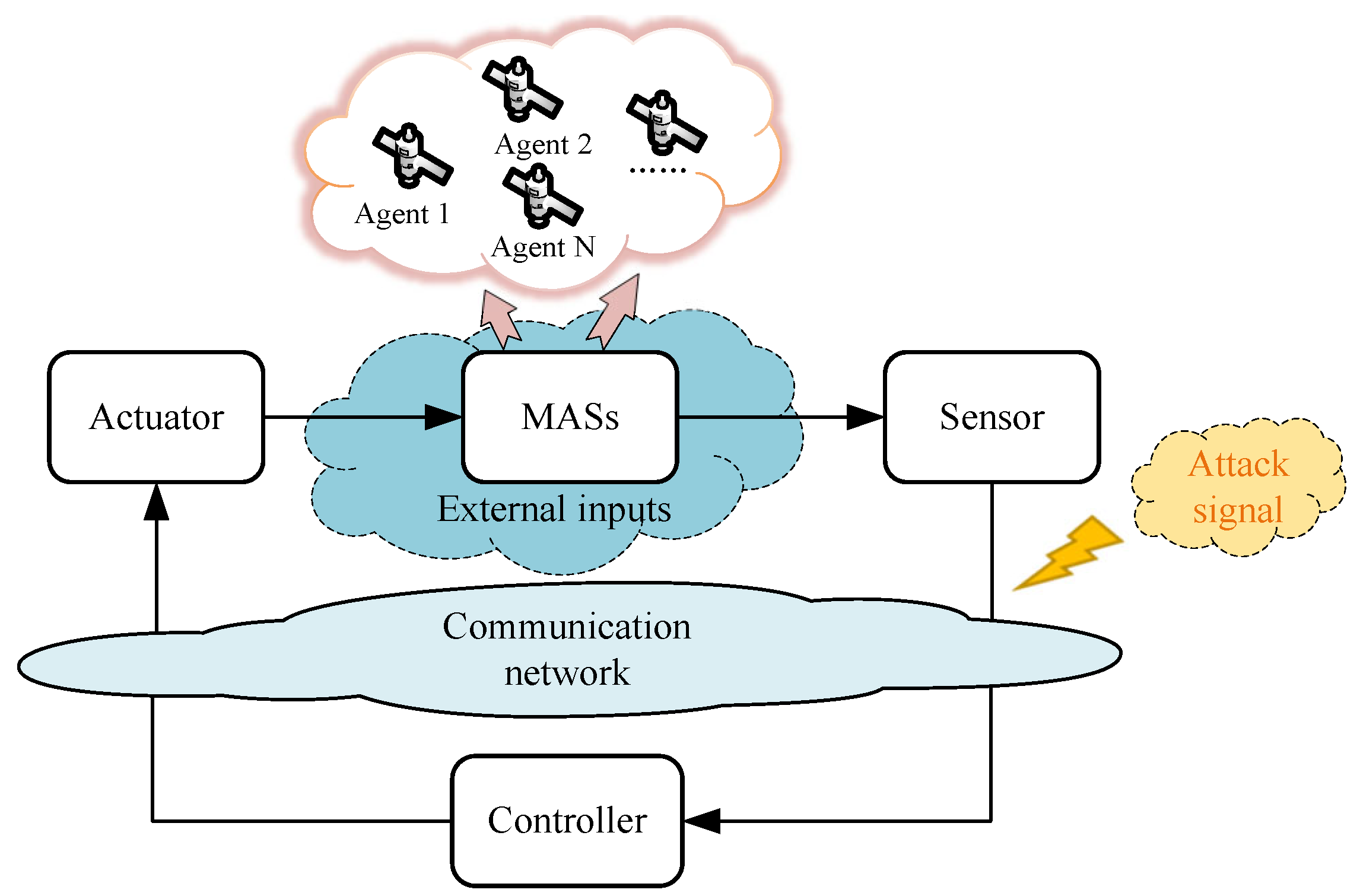
2.2. The Model of MASs
3. Main Results
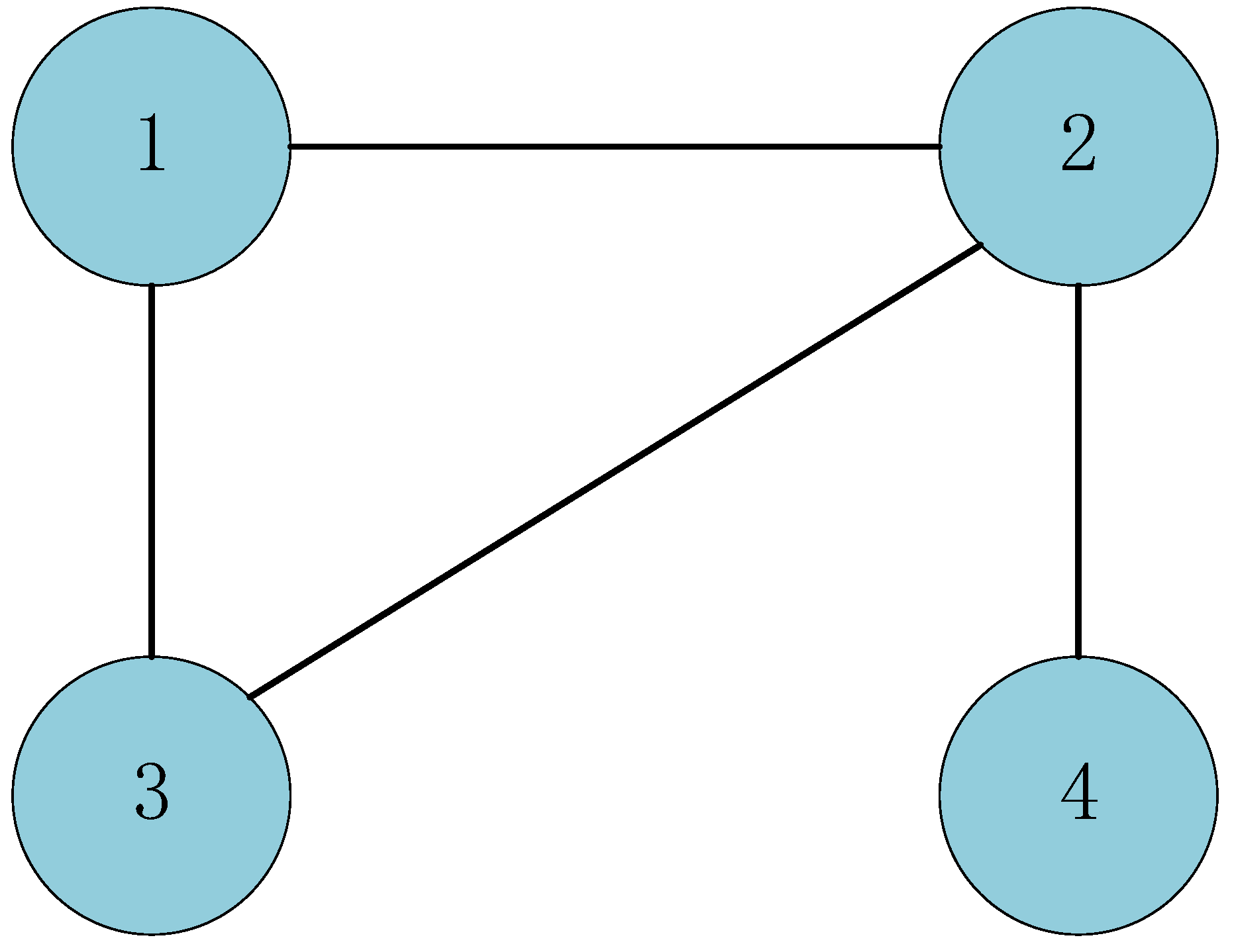
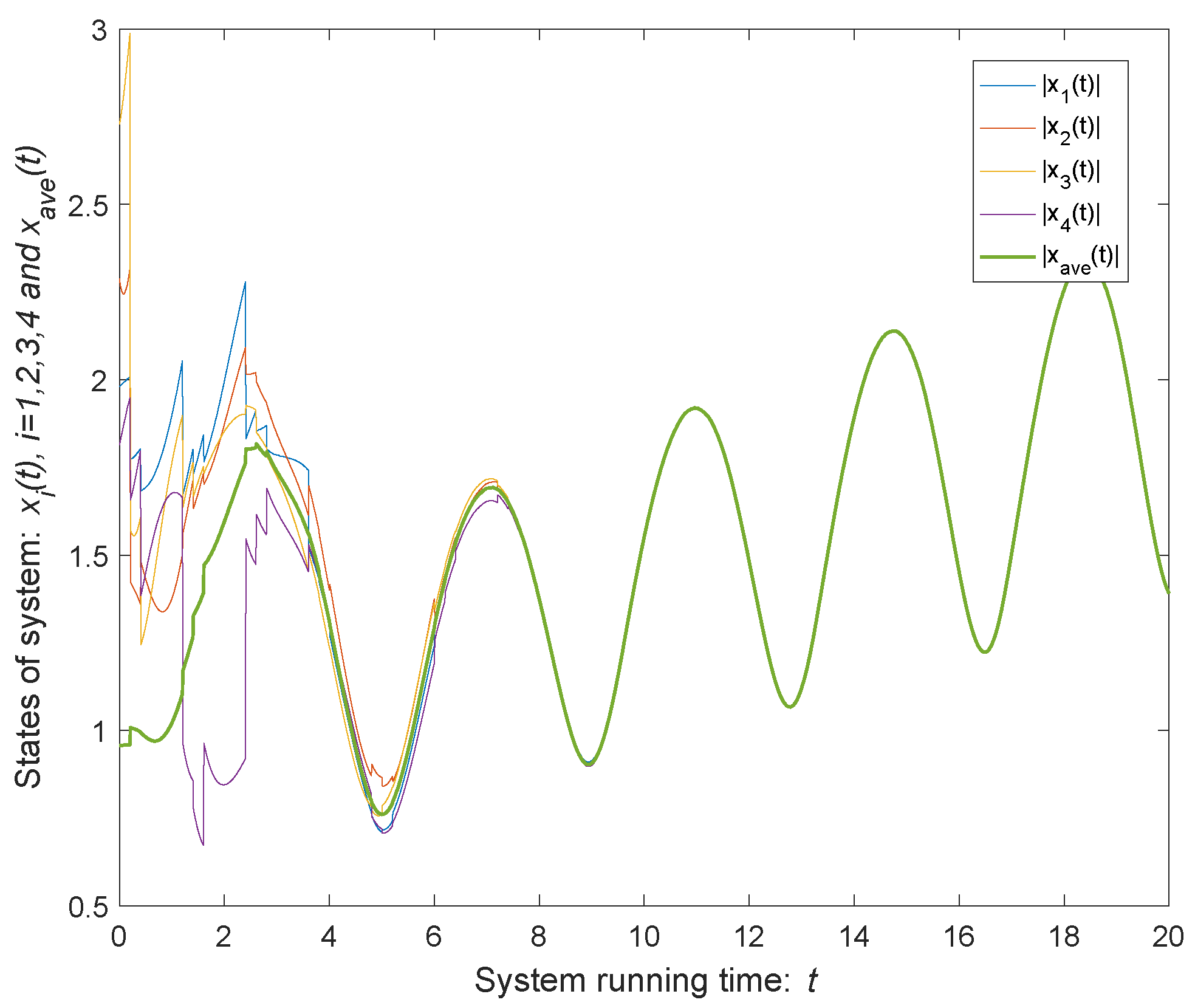
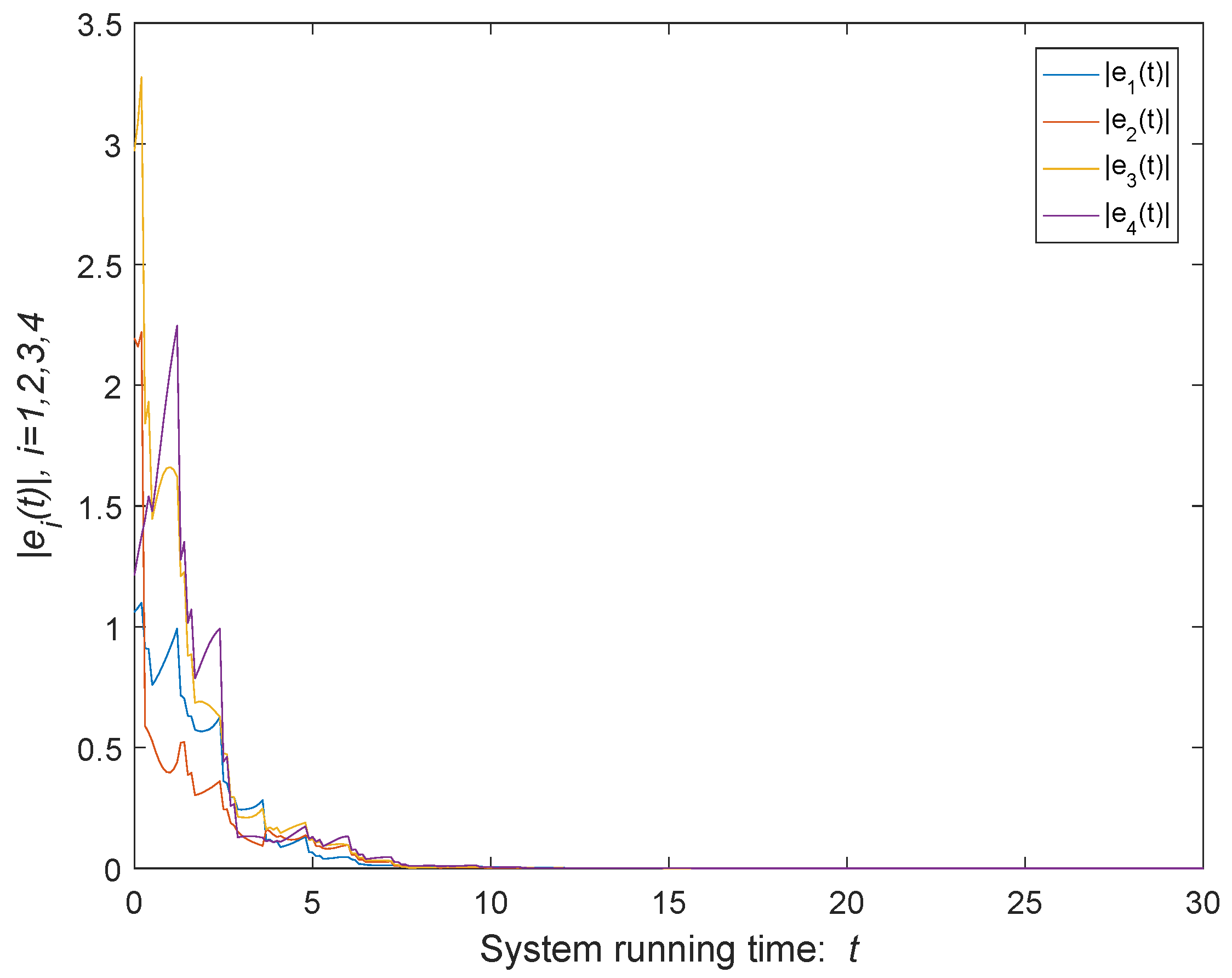
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MASs | Multi-agent systems |
| DoS | Denial-of-service |
References
- Xu, S.; Lam, J.; Zou, Y.; Li, J. Robust admissibility of time-varying singular systems with commensurate time delays. Automatica 2009, 45, 2714–2717. [Google Scholar] [CrossRef]
- Mazenc, F.; Malisoff, M.; Niculescu, S.I. Reduction model approach for linear time-varying systems with delays. IEEE Trans. Autom. Control 2014, 59, 2068–2082. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Y. Relaxed conditions for the input-to-state stability of switched nonlinear time-varying systems. IEEE Trans. Autom. Control 2016, 62, 4706–4712. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.; Karimi, H.R. Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans. Autom. Control 2019, 64, 5207–5213. [Google Scholar] [CrossRef]
- Zhou, B. On asymptotic stability of linear time-varying systems. Automatica 2016, 68, 266–276. [Google Scholar] [CrossRef]
- Zhou, B. Stability analysis of non-linear time-varying systems by Lyapunov functions with indefinite derivatives. IET Control Theory Appl. 2017, 11, 1434–1442. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Egorov, A.V. Razumikhin and Krasovskii stability theorems for time-varying time-delay systems. Automatica 2016, 71, 281–291. [Google Scholar] [CrossRef]
- Peng, S.; Deng, F. New criteria on p th moment input-to-state stability of impulsive stochastic delayed differential systems. IEEE Trans. Autom. Control 2017, 62, 3573–3579. [Google Scholar] [CrossRef]
- Zhang, W.; Han, Q.L.; Tang, Y.; Liu, Y. Sampled-data control for a class of linear time-varying systems. Automatica 2019, 103, 126–134. [Google Scholar] [CrossRef]
- Yang, J. A Consensus Control for a Multi-Agent System With Unknown Time-Varying Communication Delays. IEEE Access 2021, 9, 55844–55852. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J. Event-triggered Weighted Average Consensus in Networks of Dynamic Agents with Time-varying Delay. IFAC-PapersOnLine 2021, 54, 127–132. [Google Scholar] [CrossRef]
- Xu, S.; Wang, B. Noisy Information Based Formation Control of Multi-Agent Systems in Time-Varying Communication Networks. IEEE Access 2021, 9, 70313–70321. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Gao, H.; Stergioulas, L.K. Robust sliding mode control for discrete stochastic systems with mixed time delays, randomly occurring uncertainties, and randomly occurring nonlinearities. IEEE Trans. Ind. Electron. 2011, 59, 3008–3015. [Google Scholar] [CrossRef] [Green Version]
- Duan, Z.; Xiang, Z.; Karimi, H.R. Robust stabilisation of 2D state-delayed stochastic systems with randomly occurring uncertainties and nonlinearities. Int. J. Syst. Sci. 2014, 45, 1402–1415. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, S.; Liu, D.; Wang, Y.; Chen, T. Leader-Following Mean-Square Consensus of Stochastic Multiagent Systems With ROUs and RONs via Distributed Event-Triggered Impulsive Control. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef]
- Almeida, R.; Girejko, E.; Hristova, S.; Malinowska, A. On leader-following consensus in multi-agent systems with discrete updates at random times. Entropy 2020, 22, 650. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, X.; Zhong, S.; Shi, K.; Liao, D.; Zhong, Q. Secure consensus of multi-agent systems with redundant signal and communication interference via distributed dynamic event-triggered control. ISA Trans. 2021, 112, 89–98. [Google Scholar] [CrossRef]
- Ahirwar, S.; Swarnkar, R.; Bhukya, S.; Namwade, G. Application of drone in agriculture. Int. J. Curr. Microbiol. Appl. Sci. 2019, 8, 2500–2505. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wen, G.; Duan, Z.; Lü, J. Distributed formation control of multiple quadrotor aircraft based on nonsmooth consensus algorithms. IEEE Trans. Cybern. 2017, 49, 342–353. [Google Scholar] [CrossRef]
- Chen, J.; Yan, S.; Yang, T.; Tan, S.C.; Hui, S.Y. Practical evaluation of droop and consensus control of distributed electric springs for both voltage and frequency regulation in microgrid. IEEE Trans. Power Electron. 2018, 34, 6947–6959. [Google Scholar] [CrossRef]
- Rahbari-Asr, N.; Zhang, Y.; Chow, M.Y. Consensus-based distributed scheduling for cooperative operation of distributed energy resources and storage devices in smart grids. IET Gener. Transm. Distrib. 2016, 10, 1268–1277. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Yan, Y. Fixed-time stability of stochastic nonlinear systems and its application into stochastic multi-agent systems. IET Control Theory Appl. 2021, 15, 126–135. [Google Scholar] [CrossRef]
- Zhang, W.; Ho, D.W.; Tang, Y.; Liu, Y. Quasi-consensus of heterogeneous-switched nonlinear multiagent systems. IEEE Trans. Cybern. 2019, 50, 3136–3146. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Y.; Han, Q.L.; Liu, Y. Sampled-Data Consensus of Linear Time-Varying Multiagent Networks With Time-Varying Topologies. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef]
- Luo, H.; Wang, Y.; Zhan, R.; Zhang, X.; Wen, H.; Yang, S. Cluster-Delay Mean Square Consensus of Stochastic Multi-Agent Systems with Impulse Time Windows. Entropy 2021, 23, 1033. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S. Admissible consensus for descriptor multi-agent systems with exogenous disturbances. Entropy 2018, 20, 276. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Fang, M.; Pan, Y.J.; Shi, K.; Wu, Z.G. Event-triggered output synchronization for nonhomogeneous agent systems with periodic denial-of-service attacks. Int. J. Robust Nonlinear Control 2021, 31, 1851–1865. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Ye, D. Distributed event-triggered control for multi-agent systems under intermittently random denial-of-service attacks. Inf. Sci. 2021, 542, 380–390. [Google Scholar] [CrossRef]
- Pang, Z.H.; Fan, L.Z.; Sun, J.; Liu, K.; Liu, G.P. Detection of stealthy false data injection attacks against networked control systems via active data modification. Inf. Sci. 2021, 546, 192–205. [Google Scholar] [CrossRef]
- He, W.; Qian, F.; Han, Q.L.; Chen, G. Almost sure stability of nonlinear systems under random and impulsive sequential attacks. IEEE Trans. Autom. Control 2020, 65, 3879–3886. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, F.; Chen, J.; Zhang, J.; Hu, A.; Hu, M. Adaptive Event-Triggered Synchronization of Uncertain Fractional Order Neural Networks with Double Deception Attacks and Time-Varying Delay. Entropy 2021, 23, 1291. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Sun, H.; Ma, L.; Zhang, J.; Bo, Y. Quasi-consensus control for a class of time-varying stochastic nonlinear time-delay multiagent systems subject to deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6863–6873. [Google Scholar] [CrossRef]
- Javanmardi, H.; Dehghani, M.; Mohammadi, M.; Siamak, S.; Hesamzadeh, M.R. BMI-based load frequency control in microgrids under false data injection attacks. IEEE Syst. J. 2021. [Google Scholar] [CrossRef]
- Li, X.M.; Zhou, Q.; Li, P.; Li, H.; Lu, R. Event-triggered consensus control for multi-agent systems against false data-injection attacks. IEEE Trans. Cybern. 2019, 50, 1856–1866. [Google Scholar] [CrossRef]
- He, W.; Mo, Z.; Han, Q.L.; Qian, F. Secure impulsive synchronization in Lipschitz-type multi-agent systems subject to deception attacks. IEEE/CAA J. Autom. Sin. 2020, 7, 1326–1334. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.L.; Wu, H.N.; Huang, T. Consensus and H∞ Consensus of Nonlinear Second-Order Multi-Agent Systems. IEEE Trans. Netw. Sci. Eng. 2020, 7, 1251–1264. [Google Scholar] [CrossRef]
- Wen, G.; Zhai, X.; Peng, Z.; Rahmani, A. Fault-tolerant secure consensus tracking of delayed nonlinear multi-agent systems with deception attacks and uncertain parameters via impulsive control. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105043. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Peng, S.; Feng, W. Quasi-Consensus of Time-Varying Multi-Agent Systems with External Inputs under Deception Attacks. Entropy 2022, 24, 447. https://doi.org/10.3390/e24040447
Zeng Z, Peng S, Feng W. Quasi-Consensus of Time-Varying Multi-Agent Systems with External Inputs under Deception Attacks. Entropy. 2022; 24(4):447. https://doi.org/10.3390/e24040447
Chicago/Turabian StyleZeng, Zixian, Shiguo Peng, and Wandian Feng. 2022. "Quasi-Consensus of Time-Varying Multi-Agent Systems with External Inputs under Deception Attacks" Entropy 24, no. 4: 447. https://doi.org/10.3390/e24040447
APA StyleZeng, Z., Peng, S., & Feng, W. (2022). Quasi-Consensus of Time-Varying Multi-Agent Systems with External Inputs under Deception Attacks. Entropy, 24(4), 447. https://doi.org/10.3390/e24040447




