Controversial Variable Node Selection-Based Adaptive Belief Propagation Decoding Algorithm Using Bit Flipping Check for JSCC Systems
Abstract
:1. Introduction
- (1)
- A novel joint coding matrix is constructed through which the source compression and channel coding can be realized simultaneously to improve the coding efficiency.
- (2)
- A bit flipping check (BFC) algorithm is proposed to check and correct the errors of the compressed source block. The unreliable bits of each source block are selected by using the channel soft information to flip. If the reconstruction results of partial and all the source information are the same, the verification is successful.
- (3)
- A controversial variable node selection-based ABP (CVNS-ABP) algorithm is presented for JSC decoding. The proposed CVNS-ABP algorithm reduces the influence of error bits on decoding by selecting error variable nodes (VNs) from controversial VNs and adding them to the sparsity of the parity-check matrix. Based on the BFC algorithm and CVNS-ABP algorithm, several JSC decoding algorithms are proposed. By making full use of the redundancy of the source, the performance of JSC decoding is greatly improved.
2. System Description
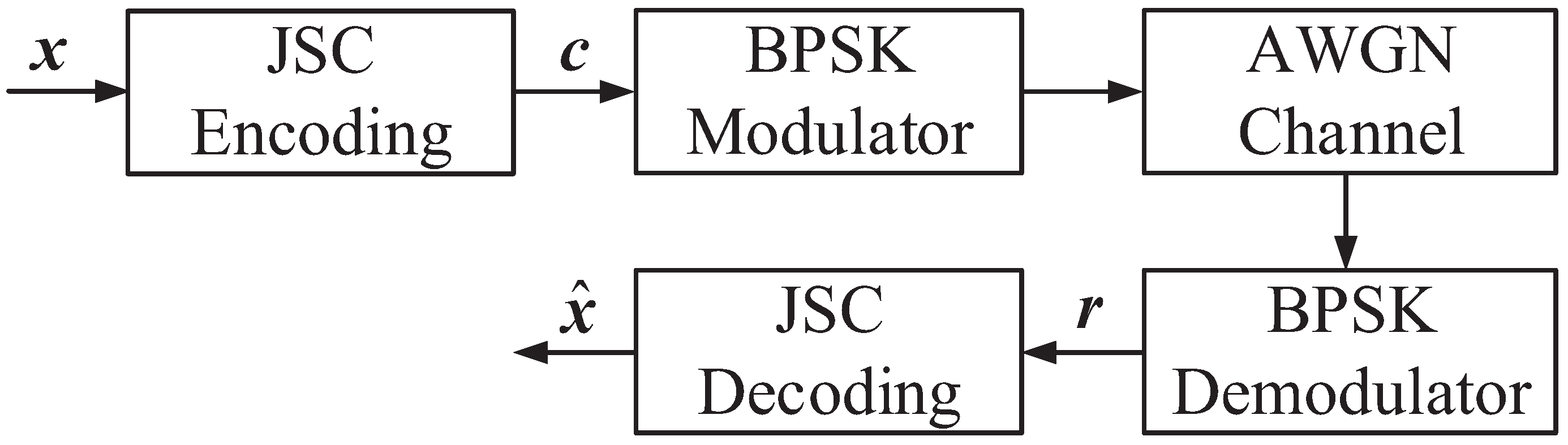
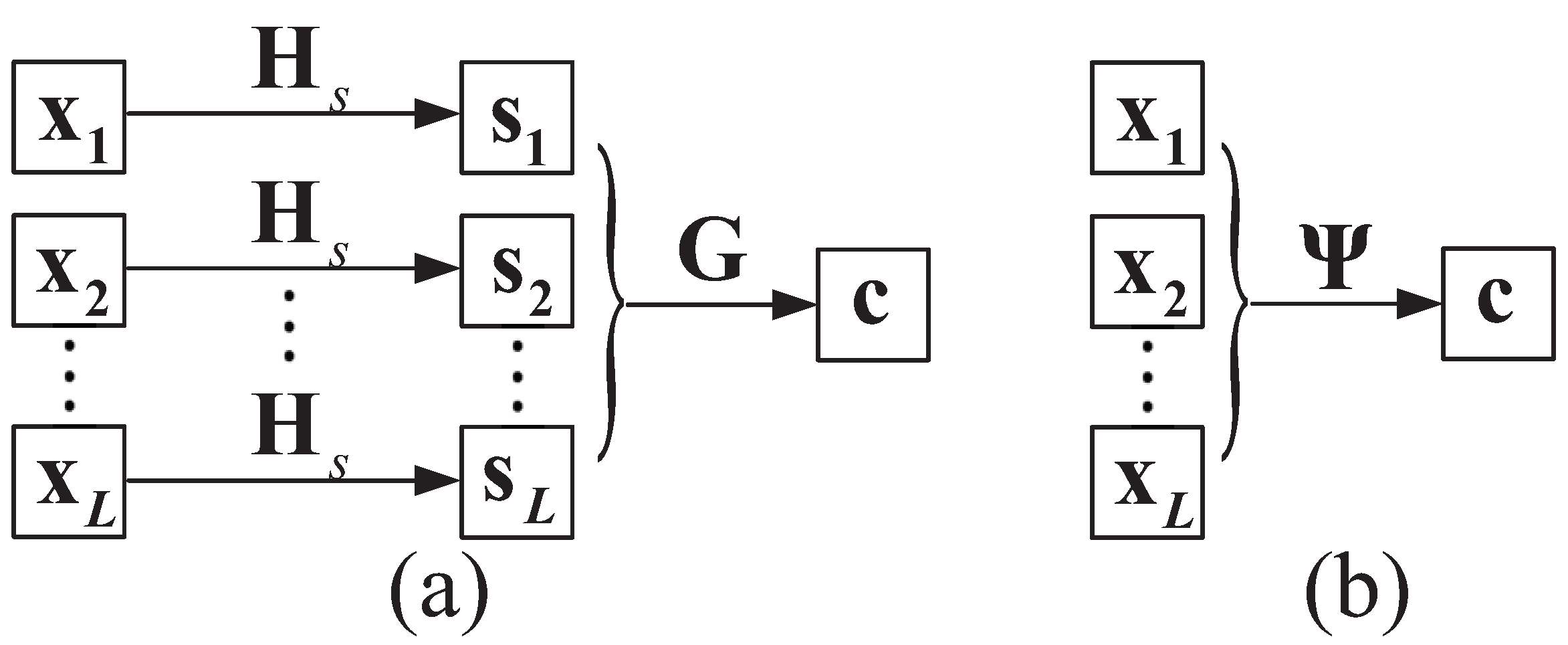
2.1. JSC Encoding
2.2. Bit Flipping Check Algorithm
| Algorithm 1: The Bit Flipping Check Algorithm |
 |
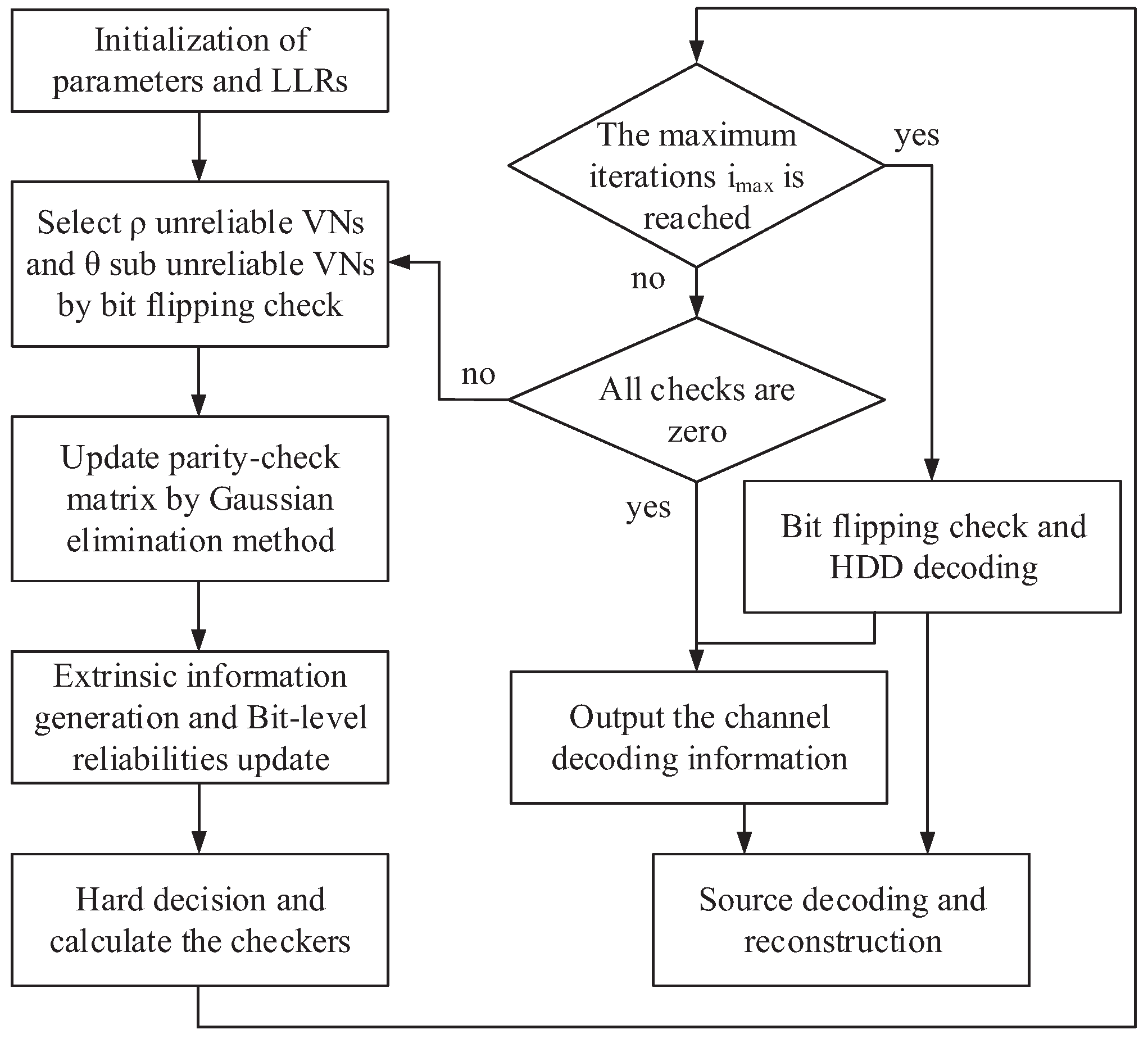
2.3. Controversial Variable Node Selection Based Adaptive Belief Propagation Decoding Algorithm
| Algorithm 2: The CVNS-ABP Algorithm |
Initialize: Set damping factor , the maximum iteration number , the LLR of the i-th iteration . Step 1. BFC for each source block Calculate the and for each source block. if = then
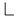 Declare the checked source block is reliable. Declare the checked source block is reliable.else 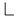 Declare the checked source block is unreliable. Declare the checked source block is unreliable.Step 2. Unreliable VN selection Sort the bit sequence according to and select unreliable VNs with the smallest absolute value. Step 3. Controversial VN selection Select the remaining controversial VNs from the unreliable source blocks, where + = . Step 4. Parity-check matrix update Implement Gaussian elimination to unitize the unreliable positions selected in the parity-check matrix. Step 5. Extrinsic information generation Calculate the extrinsic LLR vector Step 6. Bit-level reliabilities update , where . Step 7. Hard decision Make a hard decision on the value of VNs Step 8. Termination criterion ifthen
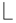 output the estimated bits. output the estimated bits.else ifthen
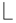 output the estimated bits. output the estimated bits.else 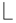 return to Step 1. return to Step 1. |
2.4. High-Performance JSC Decoding Scheme
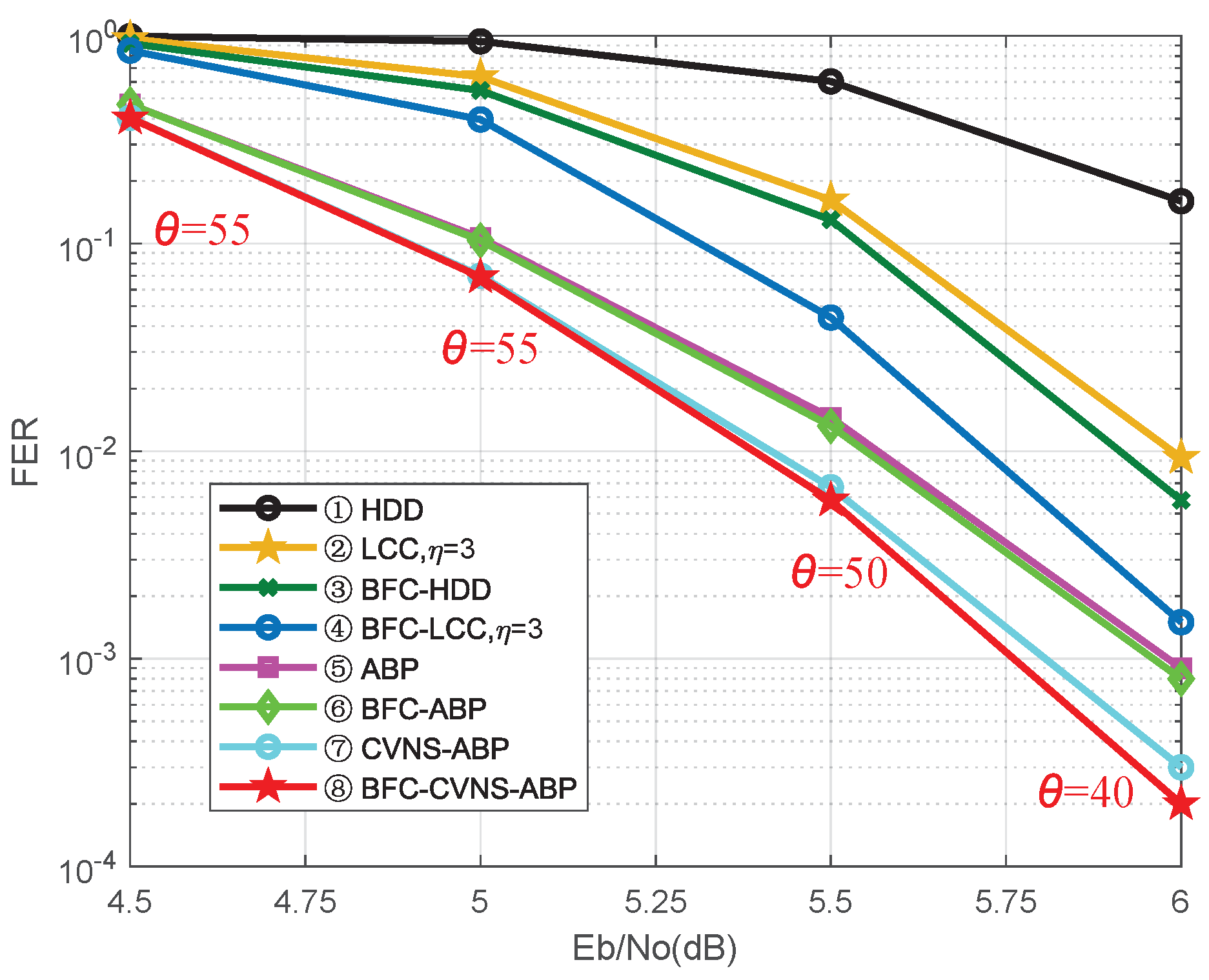
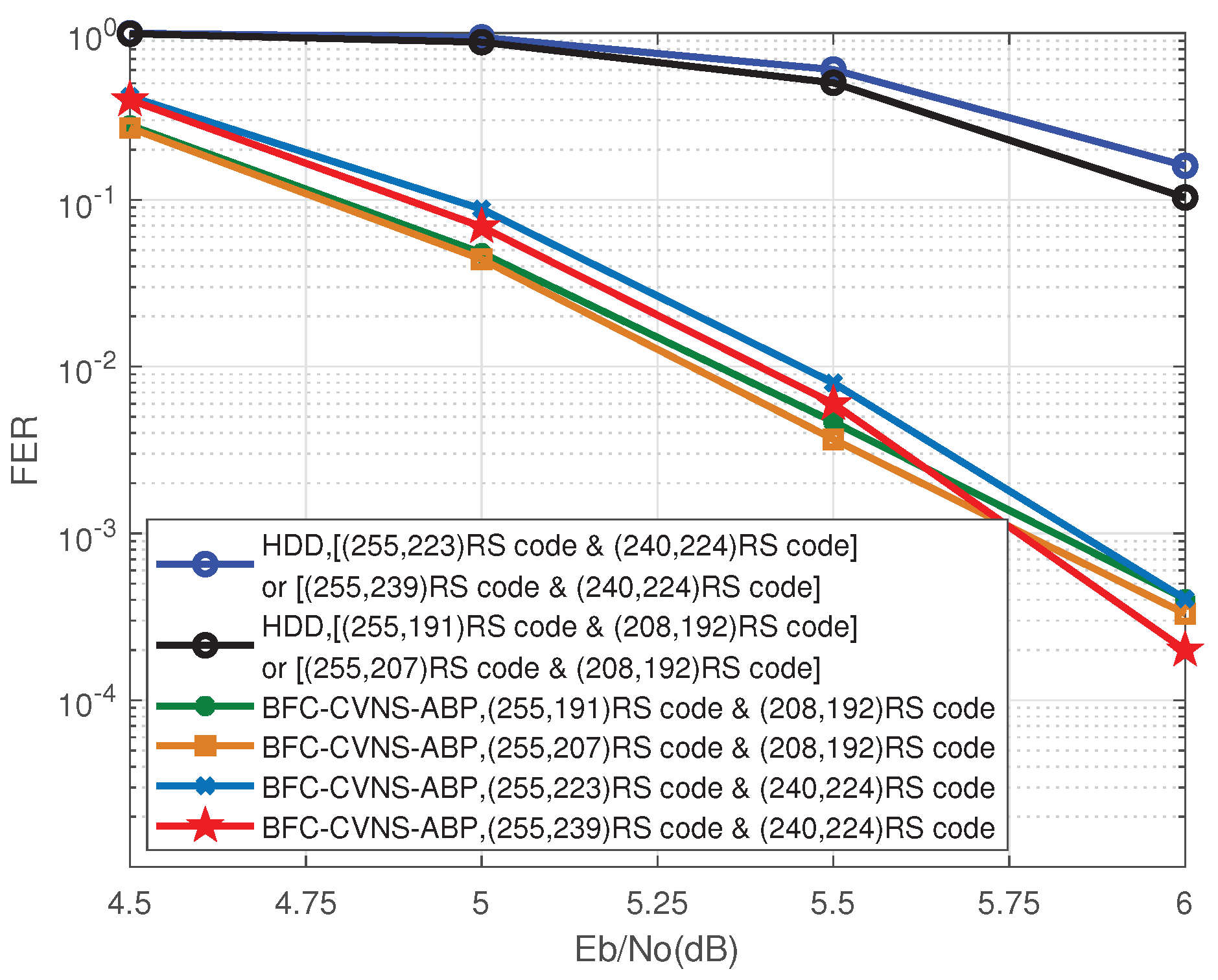
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fresia, M.; Perez-Cruz, F.; Poor, H.V.; Verdu, S. Joint source and channel coding. IEEE Signal Process. Mag. 2010, 27, 104–113. [Google Scholar] [CrossRef]
- Zhong, Y.; Alajaji, F.; Campbell, L.L. On the joint source–channel coding error exponent for discrete memoryless systems. IEEE Trans. Inf. Theory 2006, 52, 1450–1468. [Google Scholar] [CrossRef] [Green Version]
- Chen, X. Zero-delay Gaussian joint source–channel coding for the interference channel. IEEE Commun. Lett. 2018, 22, 712–715. [Google Scholar] [CrossRef] [Green Version]
- Fresnedo, O.; Suarez-Casal, P.; Castedo, L. Transmission of spatiotemporal correlated sources over fading multiple access channels with DQLC mappings. IEEE Trans. Commun. 2019, 67, 5604–5617. [Google Scholar] [CrossRef]
- Deng, L.; Shi, Z.; Li, O.; Ji, J. Joint Coding and Adaptive Image Transmission Scheme Based on DP-LDPC Codes for IoT Scenarios. IEEE Access 2019, 7, 18437–18449. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L. Design and analysis of joint source channel coding schemes over non-standard coding channels. IEEE Trans. Veh. Technol. 2020, 21, 5369–5380. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Chen, J.; Hong, S. Joint Component Design for the JSCC System Based on DP-LDPC Codes. IEEE Trans. Commun. 2020, 68, 5808–5818. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, M.; Narayanan, K.R.; Jiang, A.; Bandic, Z. Joint source-channel decoding of polar codes for language-based sources. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Jin, L.; Yang, P.; Yang, H. Distributed Joint Source-Channel Decoding Using Systematic Polar Codes. IEEE Commun. Lett. 2018, 22, 49–52. [Google Scholar] [CrossRef]
- Dong, Y.; Niu, K.; Dai, J.; Wang, S.; Yuan, Y. Joint Source and Channel Coding Using Double Polar Codes. IEEE Commun. Lett. 2021, 25, 2810–2814. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Liang, Y.; Liu, Y. Efficient Reconstruction Architecture of Compressed Sensing and Integrated Source-Channel Decoder Based on Reed Solomon Code. IEEE Commun. Lett. 2020, 24, 1245–1249. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; An, X.; Liu, Y. Sparsity Adaptive Compressed Sensing and Reconstruction Architecture Based on Reed-Solomon Codes. IEEE Commun. Lett. 2020, 25, 716–720. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Liu, Y. Joint Coding Scheme Based on Reed-Solomon Codes. In Proceedings of the 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), Chengdu, China, 23–26 April 2021; pp. 10–16. [Google Scholar] [CrossRef]
- Jiang, J.; Narayanan, K.R. Iterative soft-input soft-output decoding of Reed-Solomon codes by adapting the parity-check matrix. IEEE Trans. Inf. Theory 2006, 52, 3746–3756. [Google Scholar] [CrossRef]
- Valls, J.; Torres, V.; Canet, M.J.; García-Herrero, F.M. A test vector generation method based on symbol error probabilities for low complexity chase soft-decision Reed-Solomon decoding. IEEE Trans. Circ. Syst. I Reg. Pap. 2019, 66, 2198–2207. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check codes. IEEE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Santini, P.; Battaglioni, M.; Baldi, M.; Chiaraluce, F. Analysis of the error correction capability of LDPC and MDPC codes under parallel bit-flipping decoding and application to cryptography. IEEE Trans. Commun. 2020, 68, 4648–4660. [Google Scholar] [CrossRef] [Green Version]
- Tillich, J.-P. The decoding failure probability of MDPC codes. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 23–26 April 2018; pp. 941–945. [Google Scholar] [CrossRef] [Green Version]
- Sarwate, D.V.; Shanbhag, N.R. High-speed architectures for Reed-Solomon decoders. IEEE Trans. Large Scale Integr. (VLSI) Syst. 2001, 9, 641–655. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, W.; Jing, Y.; Chang, Y.; Liu, Y. Controversial Variable Node Selection-Based Adaptive Belief Propagation Decoding Algorithm Using Bit Flipping Check for JSCC Systems. Entropy 2022, 24, 427. https://doi.org/10.3390/e24030427
Wang H, Zhang W, Jing Y, Chang Y, Liu Y. Controversial Variable Node Selection-Based Adaptive Belief Propagation Decoding Algorithm Using Bit Flipping Check for JSCC Systems. Entropy. 2022; 24(3):427. https://doi.org/10.3390/e24030427
Chicago/Turabian StyleWang, Hao, Wei Zhang, Yizhe Jing, Yanyan Chang, and Yanyan Liu. 2022. "Controversial Variable Node Selection-Based Adaptive Belief Propagation Decoding Algorithm Using Bit Flipping Check for JSCC Systems" Entropy 24, no. 3: 427. https://doi.org/10.3390/e24030427
APA StyleWang, H., Zhang, W., Jing, Y., Chang, Y., & Liu, Y. (2022). Controversial Variable Node Selection-Based Adaptive Belief Propagation Decoding Algorithm Using Bit Flipping Check for JSCC Systems. Entropy, 24(3), 427. https://doi.org/10.3390/e24030427






