Dissipation-Induced Information Scrambling in a Collision Model
Abstract
:1. Introduction
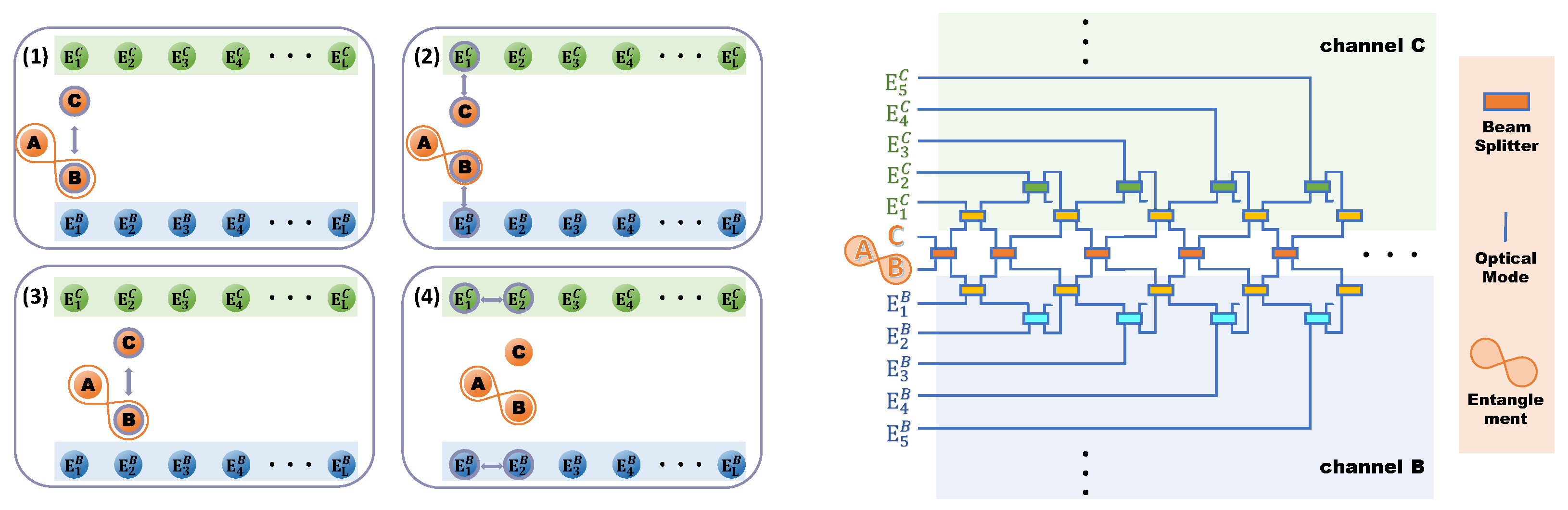
2. Collision Model
- (1)
- Collision between B and C occurs.
- (2)
- B and C individually collide with j-th environmental particles .
- (3)
- B and C collide with each other again.
- (4)
- Environmental particles interact with -th mode .
3. Formalism
3.1. Characteristic Function of Gaussian State
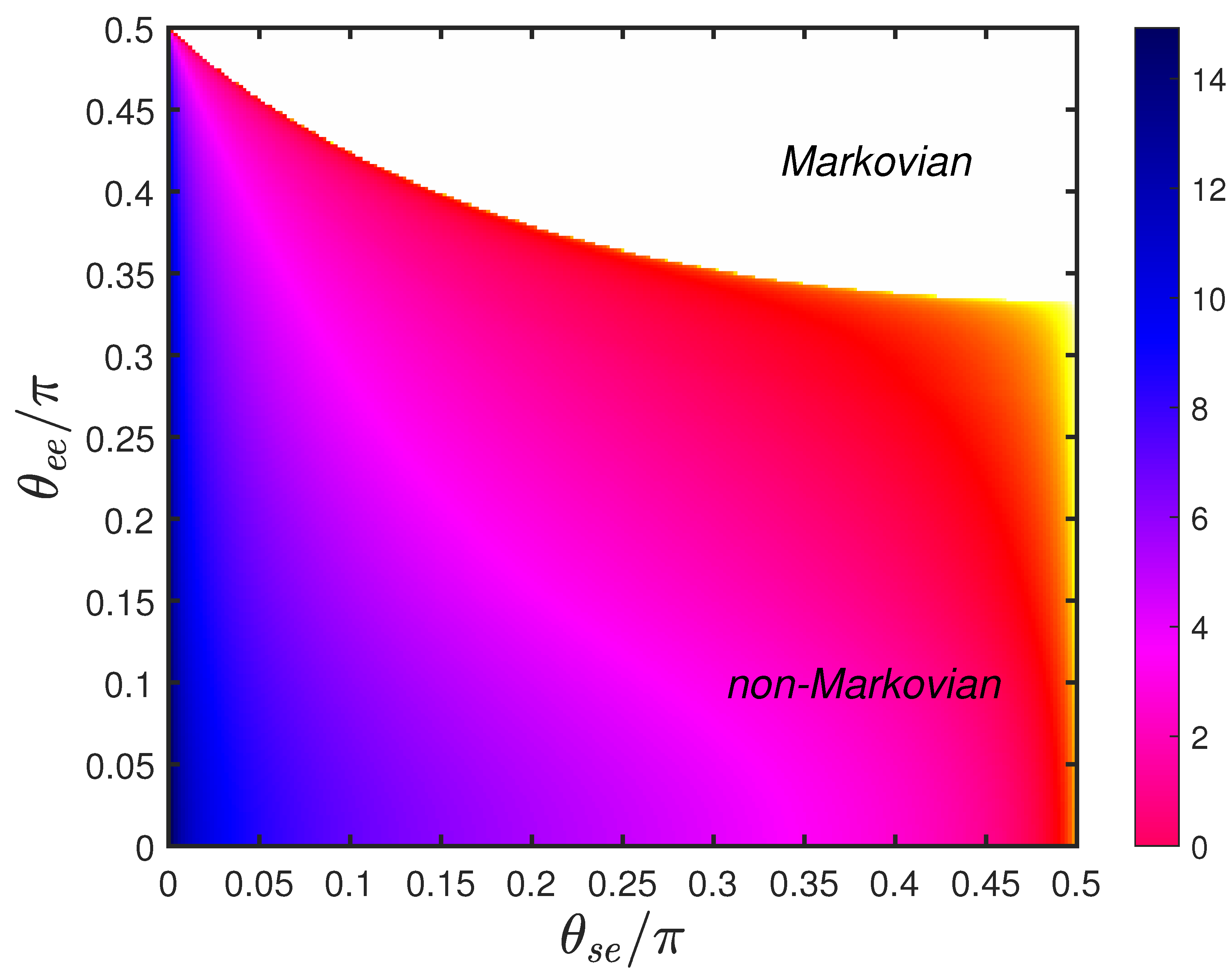
3.2. Non-Markovianity of Dissipative Channel
3.3. Tripartite Mutual Information
4. Results and Discussions
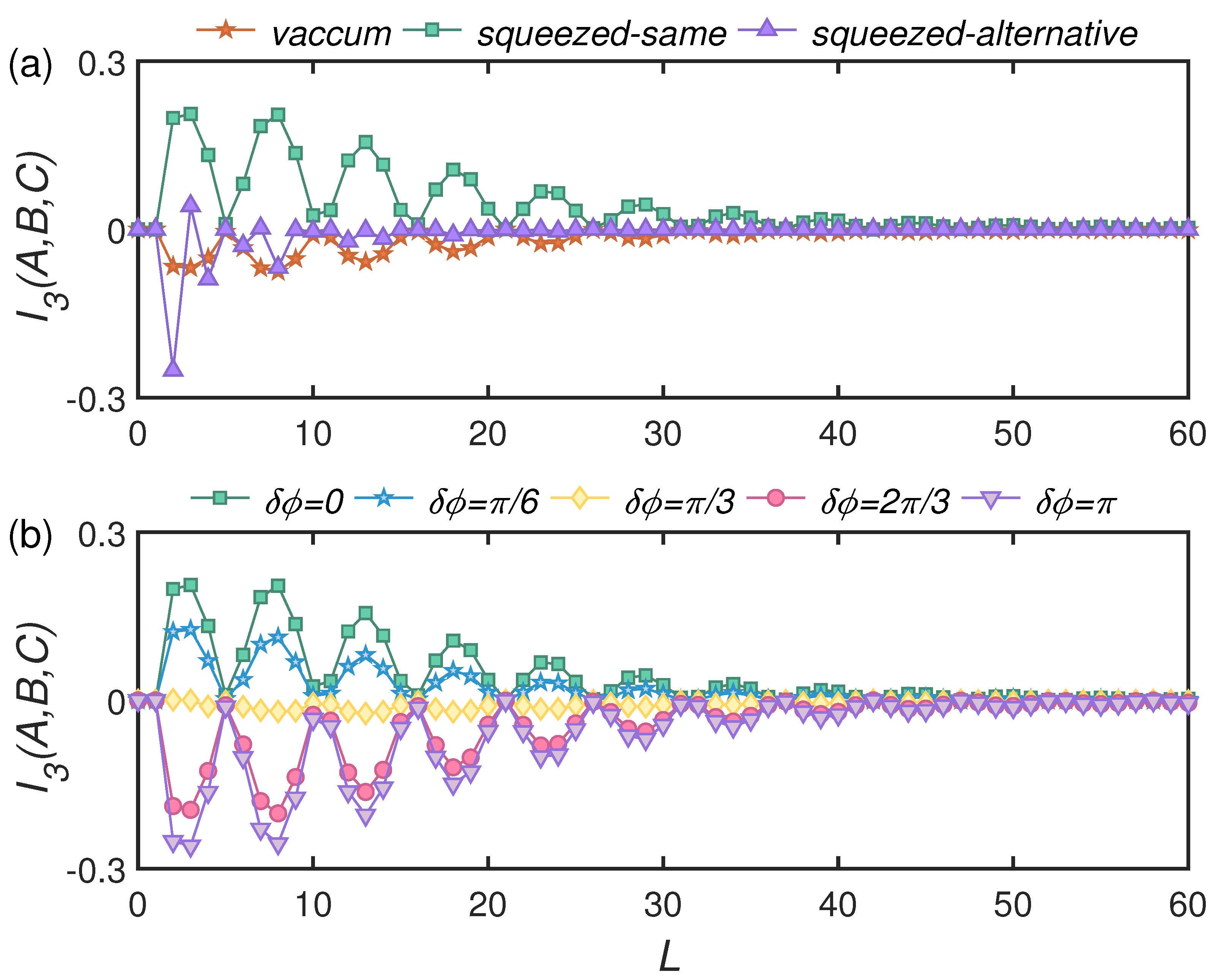
4.1. Markovian Case
- vacuum state: , and ;
- squeezed same state: squeezed vacuum states with identical squeezing angles , , = const.;
- squeezed alternative state: Squeezed vacuum states with the squeezed directions of neighboring modes being perpendicular to each other , , for odd index j and for even index j.
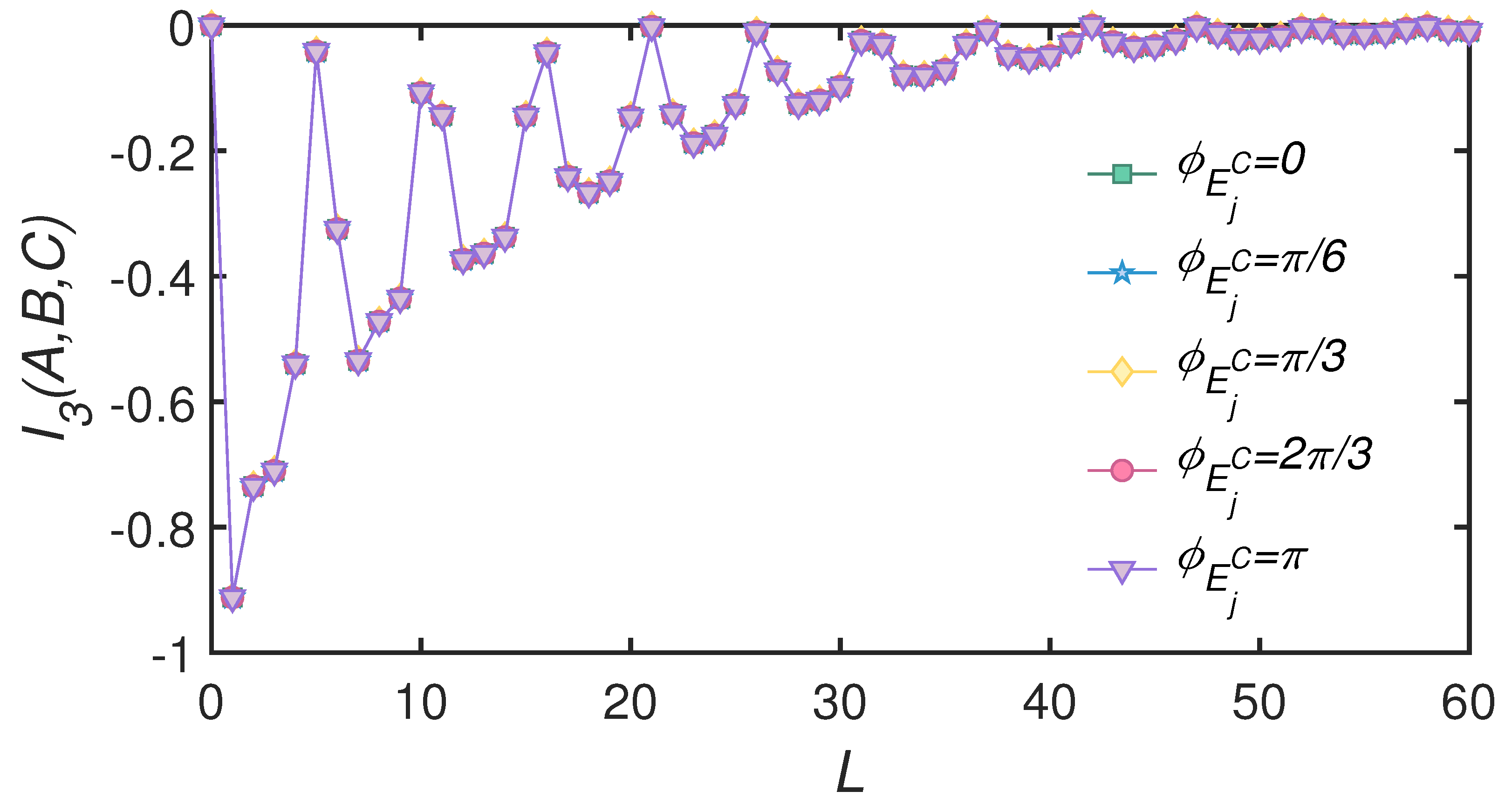
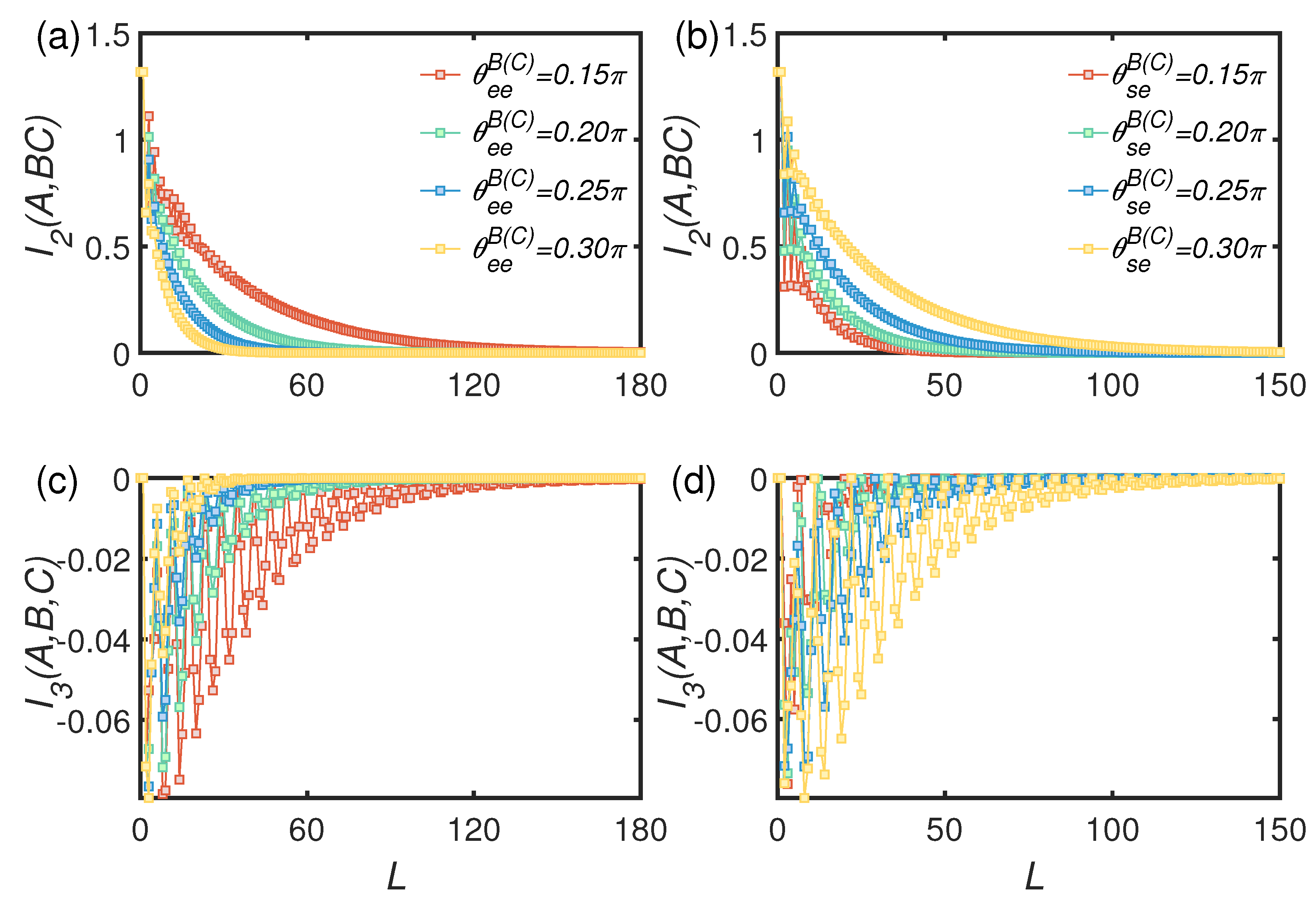
4.2. Non-Markovian Case
5. Summary
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Hosur, P.; Qi, X.-L.; Roberts, D.A.; Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef] [Green Version]
- Sachdev, S.; Ye, J. Gapless spin-fluid ground state in a random quantum Heisenberg magnet. Phys. Rev. Lett. 1993, 70, 3339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swingle, B.; Bentsen, G.; Monika, S.-S.; Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 2016, 94, 040302. [Google Scholar] [CrossRef] [Green Version]
- Daǧ, C.B.; Duan, L.-M. Detection of out-of-time-order correlators and information scrambling in cold atoms: Ladder-XX model. Phys. Rev. A 2019, 99, 052322. [Google Scholar] [CrossRef] [Green Version]
- Alonso, J.R.G.; Halpern, N.Y.; Dressel, J. Out-of-Time-Ordered-Correlator Quasiprobabilities Robustly Witness Scrambling. Phys. Rev. Lett. 2019, 122, 040404. [Google Scholar] [CrossRef] [Green Version]
- Landsman, K.A.; Figgatt, C.; Schuster, T.; Linke, N.M.; Yoshida, B.; Yao, N.Y.; Monroe, C. Verified quantum information scrambling. Nature 2019, 567, 61. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 8, 106. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D.A.; Stanford, D. Diagnosing Chaos Using Four-Point Functions in Two-Dimensional Conformal Field Theory. Phys. Rev. Lett. 2015, 115, 131603. [Google Scholar] [CrossRef]
- Polchinski, J.; Rosenhaus, V. The spectrum in the SachdevYe-Kitaev model. J. High Energy Phys. 2016, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Mezei, M.; Stanford, D. On entanglement spreading in chaotic systems. J. High Energy Phys. 2017, 5, 65. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D.A.; Yoshida, B. Chaos and complexity by design. J. High Energy Phys 2017, 4, 121. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Zhang, P.; Fan, R.; Zhai, H. Out-of-time-order correlation at a quantum phase transition. Phys. Rev. B 2017, 96, 054503. [Google Scholar] [CrossRef] [Green Version]
- Heyl, M.; Pollmann, F.; Dóra, B. Detecting Equilibrium and Dynamical Quantum Phase Transitions in Ising Chains via Out-of-Time-Ordered Correlators. Phys. Rev. Lett. 2018, 121, 016801. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Pérez-Bernal, F. Probing an excited-state quantum phase transition in a quantum many-body system via an out-of-time-order correlator. Phys. Rev. A 2019, 100, 062113. [Google Scholar] [CrossRef] [Green Version]
- Daǧ, C.B.; Sun, K.; Duan, L.-M. Detection of Quantum Phase Via Out-of-Time-Order Correlators. Phys. Rev. Lett. 2019, 123, 140602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sahu, S.; Xu, S.; Swingle, B. Scrambling dynamics across a thermalization-localization quantum phase transition. Phys. Rev. Lett. 2019, 123, 165902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, S.; Bao, Y.; Qi, X.-L.; Altman, E. Quantum Error Correction in Scrambling Dynamics and Measurement-Induced Phase Transition. Phys. Rev. Lett. 2020, 125, 030505. [Google Scholar] [CrossRef]
- Shukla, R.K.; Naik, G.K.; Mishra, S.K. Out-of-time-order correlation and detection of phase structure in Floquet transverse Ising spin system. EPL 2021, 132, 4. [Google Scholar]
- Huang, Y.; Zhang, Y.-L.; Chen, X. Out-of-time-ordered correlators in many-body localized systems. Ann. Phys. 2016, 529, 1600318. [Google Scholar] [CrossRef]
- Fan, R.; Zhang, P.; Shen, H.; Zhai, H. Out-of-time-order correlation for many-body localization. Sci. Bull. 2017, 62, 707. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhou, T.; Huse, D.A.; Fradkin, E. Out-of-time-order correlations in many-body localized and thermal phases. Ann. Phys. 2016, 529, 1600332. [Google Scholar] [CrossRef] [Green Version]
- He, R.-Q.; Lu, Z.-Y. Characterizing many-body localization by out-of-time-ordered correlation. Phys. Rev. B 2017, 95, 054201. [Google Scholar] [CrossRef] [Green Version]
- Swingle, B.; Chowdhury, D. Slow scrambling in disordered quantum systems. Phys. Rev. B 2017, 95, 060201. [Google Scholar] [CrossRef] [Green Version]
- Gärttner, M.; Bohnet, J.G.; Safavi-Naini, A.; Wall, M.L.; Bollinger, J.J.; Rey, A.M. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 2017, 13, 781. [Google Scholar] [CrossRef]
- Li, J.; Fan, R.; Wang, H.; Ye, B.; Zeng, B.; Zhai, H.; Peng, X.; Du, J. Measuring Out-of-Time-Order Correlators on a Nuclear Magnetic Resonance Quantum Simulator. Phys. Rev. X 2017, 7, 031011. [Google Scholar] [CrossRef]
- Iyoda, E.; Sagawa, T. Scrambling of quantum information in quantum many-body systems. Phys. Rev. A 2018, 97, 042330. [Google Scholar] [CrossRef] [Green Version]
- Schnaack, O.; Bölter, N.; Paeckel, S.; Manmana, S.R.; Kehrein, S.; Schmitt, M. Tripartite information, scrambling, and the role of Hilbert space partitioning in quantum lattice models. Phys. Rev. B 2019, 100, 224302. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Zhang, P.; You, Y.-Z.; Zhai, H. Information scrambling in quantum neural networks. Phys. Rev. Lett. 2020, 124, 200504. [Google Scholar] [CrossRef]
- Wanisch, D.; Fritzsche, S. Delocalization of quantum information in long-range interacting systems. Phys. Rev. A 2021, 104, 042409. [Google Scholar] [CrossRef]
- Sun, Z.-H.; Cui, J.; Fan, H. Quantum information scrambling in the presence of weak and strong thermalization. Phys. Rev. A 2021, 104, 022405. [Google Scholar] [CrossRef]
- Matsuda, H. Physical nature of higher-order mutual information: Intrinsic correlations and frustration. Phys. Rev. E 2000, 62, 3096. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H. Information theoretic characterization of frustrated systems. Phys. A 2001, 294, 180. [Google Scholar] [CrossRef]
- Knap, M. Entanglement production and information scrambling in a noisy spin system. Phys. Rev. B 2018, 98, 184416. [Google Scholar] [CrossRef] [Green Version]
- Swingle, B.; Halpern, N.Y. Resilience of scrambling measurements. Phys. Rev. A 2018, 97, 062113. [Google Scholar] [CrossRef] [Green Version]
- Syzranov, S.V.; Gorshkov, A.V.; Galitski, V. Out-of-time-order correlators in finite open systems. Phys. Rev. B 2018, 97, 161114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.-L.; Huang, Y.; Chen, X. Information scrambling in chaotic systems with dissipation. Phys. Rev. B 2019, 99, 014303. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, X.; Jin, J. Information scrambling in a collision model. Phys. Rev. A 2020, 101, 042324. [Google Scholar] [CrossRef] [Green Version]
- Bhandari, B.; Fazio, R.; Taddei, G.; Arrachea, L. From nonequilibrium Green’s functions to quantum master equations for the density matrix and out-of-time-order correlators: Steady-state and adiabatic dynamics. Phys. Rev. B 2021, 104, 035425. [Google Scholar] [CrossRef]
- Domínguez, D.F.; Álvarez, G.A. Dynamics of quantum information scrambling under decoherence effects measured via active spin clusters. Phys. Rev. A 2021, 104, 062406. [Google Scholar] [CrossRef]
- Scarani, V.; Ziman, M.; Štelmachovič, P.; Gisin, N.; Bužek, V. Thermalizing Quantum Machines: Dissipation and Entanglement. Phys. Rev. Lett. 2002, 88, 097905. [Google Scholar] [CrossRef] [Green Version]
- Ciccarello, G.; Palma, G.M.; Giovannetti, V. Collision-model-based approach to non-Markovian quantum dynamics. Phys. Rev. A 2013, 87, 040103. [Google Scholar] [CrossRef]
- Ciccarello, F.; Giovannetti, V. A quantum non-Markovian collision model: Incoherent swap case. Phys. Scr. 2013, T153, 014010. [Google Scholar] [CrossRef] [Green Version]
- McCloskey, R.; Paternostro, M. Non-Markovianity and system-environment correlations in a microscopic collision model. Phys. Rev. A 2014, 89, 052120. [Google Scholar] [CrossRef] [Green Version]
- Bernardes, N.K.; Carvalho, A.R.R.; Monken, C.H.; Santos, M.F. Environmental correlations and Markovian to non-Markovian transitions in collisional models. Phys. Rev. A 2014, 90, 032111. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Giovannetti, V.; Fazio, R.; Sciarrino, F.; Mataloni, P.; Crespi, A.; Osellame, R. All-optical non-Markovian stroboscopic quantum simulator. Phys. Rev. A 2015, 91, 012122. [Google Scholar] [CrossRef] [Green Version]
- Çakmak, B.; Pezzutto, M.; Paternostro, M.; Müstecaplıoğlu, Ö.E. Non-Markovianity, coherence, and system-environment correlations in a long-range collision model. Phys. Rev. A 2017, 96, 022109. [Google Scholar] [CrossRef] [Green Version]
- Bernardes, N.K.; Carvalho, A.R.R.; Monken, C.H.; Santos, M.F. Coarse graining a non-Markovian collisional model. Phys. Rev. A 2017, 95, 032117. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Yu, C.-s. Non-Markovianity in the collision model with environmental block. New J. Phys. 2018, 20, 053026. [Google Scholar] [CrossRef]
- Man, Z.-X.; Xia, Y.-J.; Franco, R.L. Temperature effects on quantum non-Markovianity via collision models. Phys. Rev. A 2018, 97, 062104. [Google Scholar] [CrossRef] [Green Version]
- Whalen, S.J. Collision model for non-Markovian quantum trajectories. Phys. Rev. A 2019, 100, 052113. [Google Scholar] [CrossRef] [Green Version]
- Camasca, R.R.; Landi, G.T. Memory kernel and divisibility of Gaussian collisional models. Phys. Rev. A 2021, 103, 022202. [Google Scholar] [CrossRef]
- Karpat, G.; Yalçınkaya, I.; Çakmak, B. Quantum synchronization in a collision model. Phys. Rev. A 2019, 100, 012133. [Google Scholar] [CrossRef] [Green Version]
- Beyer, K.; Luoma, K.; Strunz, W.T. Collision-model approach to steering of an open driven qubit. Phys. Rev. A 2018, 97, 032113. [Google Scholar] [CrossRef] [Green Version]
- Lorenzo, S.; Ciccarello, F.; Palma, G.M. Composite quantum collision models. Phys. Rev. A 2017, 96, 032107. [Google Scholar] [CrossRef] [Green Version]
- Çakmak, B.; Campbell, S.; Vacchini, B.; Müstecaplıoǧlu, Ö.E.; Paternostro, M. Robust multipartite entanglement generation via a collision model. Phys. Rev. A 2019, 99, 012319. [Google Scholar] [CrossRef] [Green Version]
- Grimmer, D.; Kempf, A.; Mann, R.B.; Martín-Martínez, E. Zeno friction and antifriction from quantum collision models. Phys. Rev. A 2019, 100, 042702. [Google Scholar] [CrossRef] [Green Version]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A Unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zou, J.; Li, H.; Xu, B.-M.; Wang, Y.-M.; Shao, B. Effect of coherence of nonthermal reservoirs on heat transport in a microscopic collision model. Phys. Rev. E 2018, 97, 022111. [Google Scholar] [CrossRef] [Green Version]
- Cusumano, S.; Cavina, V.; Keck, M.; de Pasquale, A.; Giovannetti, V. Entropy production and asymptotic factorization via thermalization: A collisional model approach. Phys. Rev. A 2018, 98, 032119. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.-X.; Xia, Y.-J.; Franco, R.L. Validity of the Landauer principle and quantum memory effects via collisional models. Phys. Rev. A 2019, 99, 042106. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, F.L.S.; de Chiara, G.; Paternostro, M.; Landi, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alves, G.O.; Landi, G.T. Bayesian estimation for collisional thermometry. Phys. Rev. A 2022, 105, 012212. [Google Scholar] [CrossRef]
- Landi, G.T. Battery Charging in Collision Models with Bayesian Risk Strategies. Entropy 2021, 23, 1627. [Google Scholar] [CrossRef] [PubMed]
- Ciccarello, F.; Lorenzo, S.; Giovannetti, V.; Palma, G.M. Quantum collision models: Open system dynamics from repeated interactions. Phys. Rep. 2022, 954, 1. [Google Scholar] [CrossRef]
- Cuevas, Á.; Geraldi, A.; Liorni, C.; Bonavena, L.D.; Pasquale, A.D.; Sciarrino, F.; Giovannetti, V.; Mataloni, P. All-optical implementation of collision-based evolutions of open quantum systems. Sci. Rep. 2019, 9, 3205. [Google Scholar] [CrossRef] [Green Version]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef] [Green Version]
- Torre, G.; Roga, W.; Illuminati, F. Non-Markovianity of Gaussian Channels. Phys. Rev. Lett. 2015, 115, 070401. [Google Scholar] [CrossRef] [Green Version]
- Serafini, A.; Illuminati, F.; de Siena, S. Symplectic invariants, entropic measures and correlations of Gaussian states. J. Phys. B. 2004, 37, L21. [Google Scholar] [CrossRef]
- Serafini, A. Multimode Uncertainty Relations and Separability of Continuous Variable States. Phys. Rev. Lett. 2006, 96, 110402. [Google Scholar] [CrossRef] [Green Version]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin, Germany, 1994. [Google Scholar]
- Marian, P.; Marian, T.A.; Scutaru, H. Distinguishability and nonclassicality of one-mode Gaussian states. Phys. Rev. A 2004, 69, 022104. [Google Scholar] [CrossRef]
- Wang, X.-B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with Gaussian states. Phys. Rep. 2007, 448, 1. [Google Scholar] [CrossRef] [Green Version]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laine, E.-M.; Piilo, J.; Breuer, H.-P. Measure for the non-Markovianity of quantum processes. Phys. Rev. A 2010, 81, 062115. [Google Scholar] [CrossRef] [Green Version]
- Haikka, P.; Cresser, J.D.; Maniscalco, S. Comparing different non-Markovianity measures in a driven qubit system. Phys. Rev. A 2011, 83, 012112. [Google Scholar] [CrossRef] [Green Version]
- Trapani, J.; Paris, M.G.A. Nondivisibility versus backflow of information in understanding revivals of quantum correlations for continuous-variable systems interacting with fluctuating environments. Phys. Rev. A 2016, 93, 042119. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, C.S.; Kruse, R.; Sansoni, L.; Barkhofen, S.; Silberhorn, C.; Jex, I. Gaussian Boson Sampling. Phys. Rev. Lett. 2017, 119, 170501. [Google Scholar] [CrossRef] [Green Version]
- Quesada, N.; Arrazola, J.M.; Killoran, N. Gaussian boson sampling using threshold detectors. Phys. Rev. A 2018, 98, 062322. [Google Scholar] [CrossRef] [Green Version]
- Kruse, R.; Hamilton, C.S.; Sansoni, L.; Barkhofen, S.; Silberhorn, C.; Jex, I. Detailed study of Gaussian boson sampling. Phys. Rev. A. 2019, 100, 032326. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.-S.; Peng, L.-C.; Li, Y.; Hu, Y.; Li, W.; Qin, J.; Wu, D.; Zhang, W.; Li, H.; Zhang, L.; et al. Experimental Gaussian Boson sampling. Sci. Bull. 2019, 64, 511. [Google Scholar] [CrossRef] [Green Version]
- Crespi, A.; Osellame, R.; Ramponi, R.; Giovannetti, V.; Fazio, R.; Sansoni, L.; de Nicola, F.; Sciarrino, F.; Mataloni, P. Anderson localization of entangled photons in an integrated quantum walk. Nature Photon. 2013, 7, 322. [Google Scholar] [CrossRef]
- Geraldi, A.; Laneve, A.; Bonavena, L.D.; Sansoni, L.; Ferraz, J.; Fratalocchi, A.; Sciarrino, F.; Cuevas, Á.; Mataloni, P. Experimental Investigation of Superdiffusion via Coherent Disordered Quantum Walks. Phys. Rev. Lett. 2019, 123, 140501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lou, Y.; Liu, S.; Jing, J. Experimental Demonstration of a Multifunctional All-Optical Quantum State Transfer Machine. Phys. Rev. Lett. 2021, 126, 210507. [Google Scholar] [CrossRef] [PubMed]
- Ru, S.; An, M.; Yang, Y.; Qu, R.; Wang, F.; Wang, Y.; Zhang, P.; Li, F. Quantum state transfer between two photons with polarization and orbital angular momentum via quantum teleportation technology. Phys. Rev. A 2021, 103, 052404. [Google Scholar] [CrossRef]
- Lin, J.-D.; Lin, W.-Y.; Ku, H.-Y.; Lambert, N.; Chen, Y.-N.; Nori, F. Quantum steering as a witness of quantum scrambling. Phys. Rev. A 2021, 104, 022614. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, X.; Jin, J. Dissipation-Induced Information Scrambling in a Collision Model. Entropy 2022, 24, 345. https://doi.org/10.3390/e24030345
Li Y, Li X, Jin J. Dissipation-Induced Information Scrambling in a Collision Model. Entropy. 2022; 24(3):345. https://doi.org/10.3390/e24030345
Chicago/Turabian StyleLi, Yan, Xingli Li, and Jiasen Jin. 2022. "Dissipation-Induced Information Scrambling in a Collision Model" Entropy 24, no. 3: 345. https://doi.org/10.3390/e24030345
APA StyleLi, Y., Li, X., & Jin, J. (2022). Dissipation-Induced Information Scrambling in a Collision Model. Entropy, 24(3), 345. https://doi.org/10.3390/e24030345





