Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy
Abstract
:1. Introduction
2. Preliminaries
2.1. Typical Centrality Measures
2.2. Information Entropy and Entropy Weighting Method
3. Method Description
3.1. Direct Influence of a Node with Respect to Local Attributes
3.2. Indirect Influence of a Node on Two-Hop Attributes
3.3. The Multiple Local Attributes Weighted Centrality
4. Experimental Evaluation
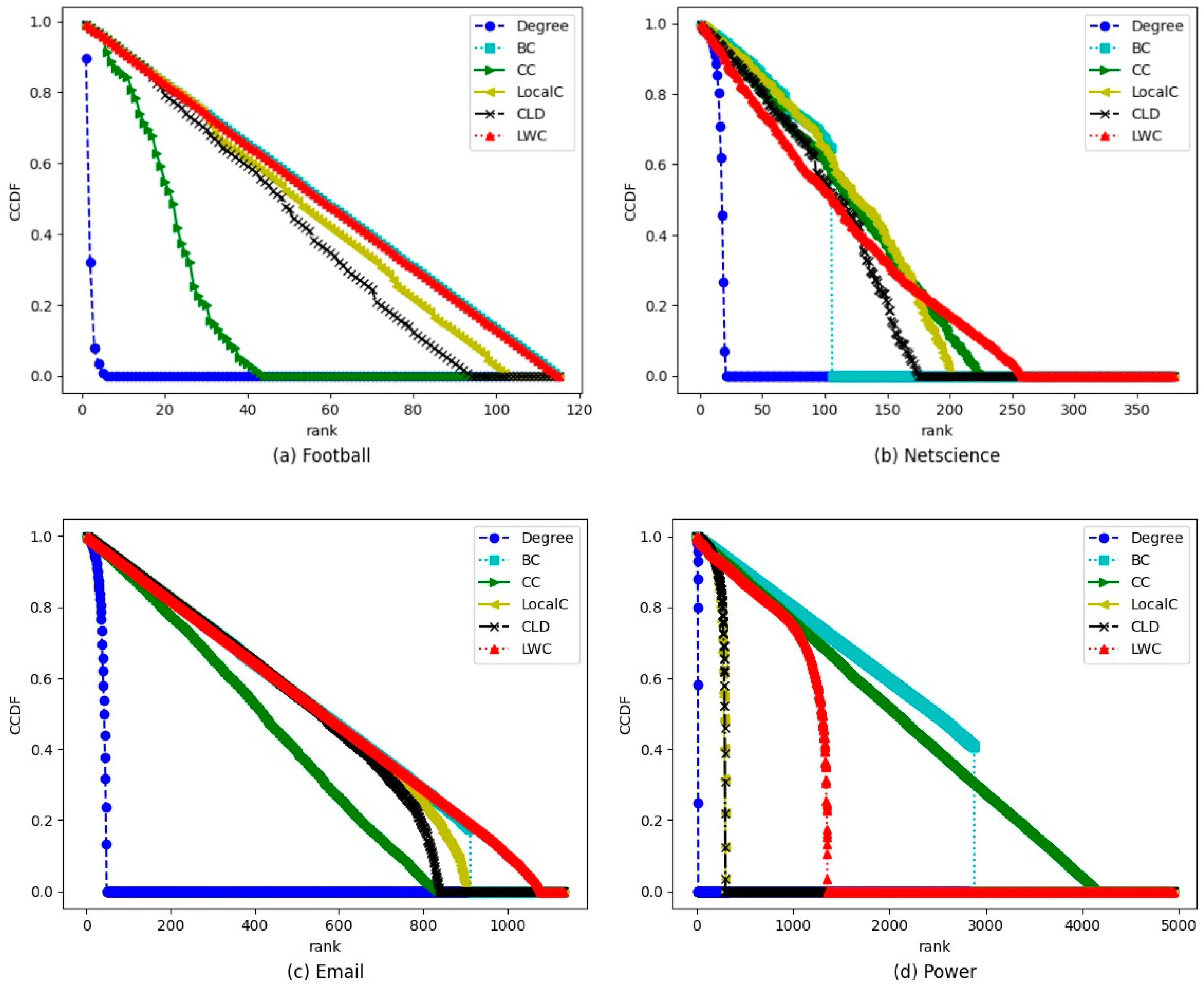
4.1. Discrimination Capability Analysis
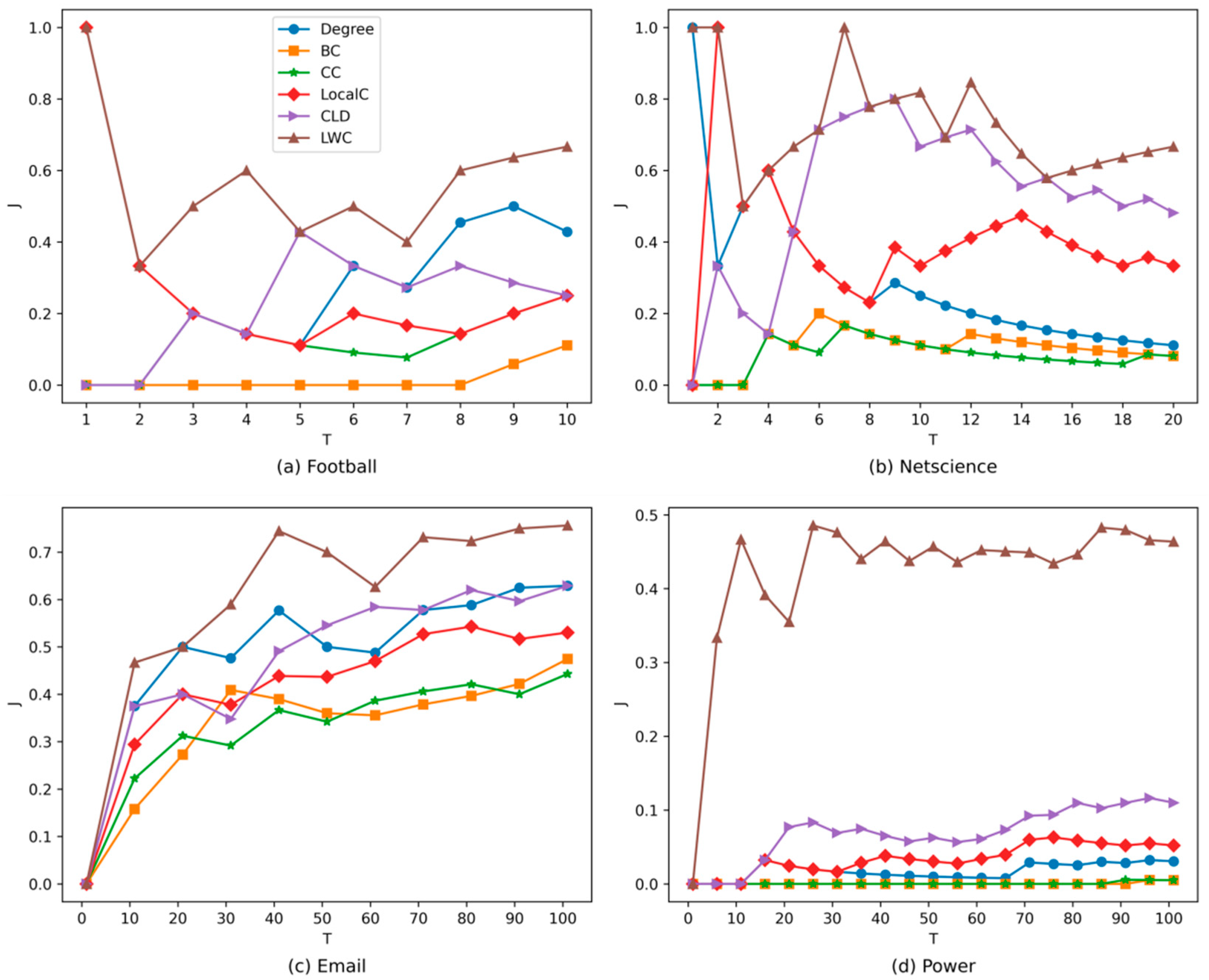
4.2. Accuracy Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tulu, M.M.; Mkiramweni, M.E.; Hou, R.; Feisso, S.; Younas, T. Influential nodes selection to enhance data dissemination in mobile social networks: A survey. J. Netw. Comput. Appl. 2020, 169, 102768. [Google Scholar] [CrossRef]
- Hafiene, N.; Karoui, W.; Ben Romdhane, L. Influential nodes detection in dynamic social networks: A survey. Expert Syst. Appl. 2020, 159, 113642. [Google Scholar] [CrossRef]
- Omar, Y.M.; Plapper, P. A Survey of Information Entropy Metrics for Complex Networks. Entropy 2020, 22, 1417. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Sabidussi, G. The centrality of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef]
- Du, Y.; Gao, C.; Chen, X.; Hu, Y.; Sadiq, R.; Deng, Y. A new closeness centrality measure via effective distance in complex networks. Chaos 2015, 25, 033112. [Google Scholar] [CrossRef]
- Newman, M.E.J. A measure of betweenness centrality based on random walks. Soc. Netw. 2005, 27, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Prountzos, D.; Pingali, K. Betweenness Centrality: Algorithms and Implementations. ACM Sigplan Not. 2013, 48, 35–45. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, T.-H.; Huang, Y.; Holme, P. Ranking Candidate Disease Genes from Gene Expression and Protein Interaction: A Katz-Centrality Based Approach. PLoS ONE 2011, 6, e24306. [Google Scholar] [CrossRef] [Green Version]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef] [Green Version]
- Maji, G.; Mandal, S.; Sen, S. A systematic survey on influential spreaders identification in complex networks with a focus on K-shell based techniques. Expert Syst. Appl. 2020, 161, 113681. [Google Scholar] [CrossRef]
- Zeng, A.; Zhang, C.-J. Ranking spreaders by decomposing complex networks. Phys. Lett. A 2013, 377, 1031–1035. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-H.; Guo, Q.; Dong, W.-Z.; Tang, L.-Y.; Liu, J.-G. Identifying the node spreading influence with largest k-core values. Phys. Lett. A 2014, 378, 3279–3284. [Google Scholar] [CrossRef]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Phys. A Stat. Mech. Its Appl. 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Wei, B.; Liu, J.; Wei, D.; Gao, C.; Deng, Y. Weighted k-shell decomposition for complex networks based on potential edge weights. Phys. A Stat. Mech. Its Appl. 2015, 420, 277–283. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Xi, J.; Du, C. Fast ranking influential nodes in complex networks using a k-shell iteration factor. Phys. A Stat. Mech. Its Appl. 2016, 461, 171–181. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, R.; Yang, Z.; Hu, R.; Li, M.; Yuan, Y.; Li, K. Identifying the most influential spreaders in complex networks by an Extended Local K-Shell Sum. Int. J. Mod. Phys. C 2017, 28, 1750014. [Google Scholar] [CrossRef]
- Wang, Z.; Du, C.; Fan, J.; Xing, Y. Ranking influential nodes in social networks based on node position and neighborhood. Neurocomputing 2017, 260, 466–477. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A. A hierarchical approach for influential node ranking in complex social networks. Expert Syst. Appl. 2018, 93, 200–211. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, B.; Li, W.; Zhang, D. Influential Node Identification in Command and Control Networks Based on Integral k-Shell. Wirel. Commun. Mob. Comput. 2019, 2019, 6528431. [Google Scholar] [CrossRef] [Green Version]
- Maji, G.; Namtirtha, A.; Dutta, A.; Curado Malta, M. Influential spreaders identification in complex networks with improved k-shell hybrid method. Expert Syst. Appl. 2020, 144, 113092. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Lü, L.; Zhang, Y.C.; Yeung, C.H.; Zhou, T. Leaders in social networks, the Delicious case. PLoS ONE 2011, 6, e21202. [Google Scholar] [CrossRef] [Green Version]
- Kleinberg, J.M. Authoritative sources in a hyperlinked environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T.; Zhang, Q.M.; Stanley, H.E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 10168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zareie, A.; Sheikhahmadi, A. EHC: Extended H-index Centrality measure for identification of users’ spreading influence in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 514, 141–155. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.-S.; Zhang, Y.-C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A Stat. Mech. Its Appl. 2012, 391, 1777–1787. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhang, R.; Hu, R.; Yang, F.; Yao, Y.; Yuan, Y. Identifying and ranking influential spreaders in complex networks by combining a local-degree sum and the clustering coefficient. Int. J. Mod. Phys. B 2018, 32, 1850118. [Google Scholar] [CrossRef]
- Qiao, T.; Shan, W.; Zhou, C. How to Identify the Most Powerful Node in Complex Networks? A Novel Entropy Centrality Approach. Entropy 2017, 19, 614. [Google Scholar] [CrossRef] [Green Version]
- Qiao, T.; Shan, W.; Yu, G.; Liu, C. A Novel Entropy-Based Centrality Approach for Identifying Vital Nodes in Weighted Networks. Entropy 2018, 20, 261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Cai, W.; Li, Y.; Du, X. Key Node Ranking in Complex Networks: A Novel Entropy and Mutual Information-Based Approach. Entropy 2020, 22, 52. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ni, C.; Yang, J.; Kong, D. Sequential seeding strategy for social influence diffusion with improved entropy-based centrality. Phys. A Stat. Mech. Its Appl. 2020, 545, 123659. [Google Scholar] [CrossRef]
- Guo, C.; Yang, L.; Chen, X.; Chen, D.; Gao, H.; Ma, J. Influential Nodes Identification in Complex Networks via Information Entropy. Entropy 2020, 22, 242. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Yang, A.; Cao, L.; Yu, S.; Xie, D. Social influence modeling using information theory in mobile social networks. Inf. Sci. 2017, 379, 146–159. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Chen, Y.; Hu, M. Identifying Key Nodes in Complex Networks Based on Global Structure. IEEE Access 2020, 8, 32904–32913. [Google Scholar] [CrossRef]
- Yang, P.; Xu, G.; Chen, H. Multi-attribute ranking method for identifying key nodes in complex networks based on GRA. Int. J. Mod. Phys. B 2019, 32, 1850363. [Google Scholar] [CrossRef]
- Mo, H.; Deng, Y. Identifying node importance based on evidence theory in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 529, 121538. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Identify influential spreaders in complex networks, the role of neighborhood. Phys. A Stat. Mech. Its Appl. 2016, 452, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Nie, H.; Zhao, J.; Wang, Q. Identifying influential spreaders in large-scale networks based on evidence theory. Neurocomputing 2019, 359, 466–475. [Google Scholar] [CrossRef]
- He, D.; Xu, J.; Chen, X. Information-Theoretic-Entropy Based Weight Aggregation Method in Multiple-Attribute Group Decision-Making. Entropy 2016, 18, 171. [Google Scholar] [CrossRef] [Green Version]
- Luo, R.; Huang, S.; Zhao, Y.; Song, Y. Threat Assessment Method of Low Altitude Slow Small (LSS) Targets Based on Information Entropy and AHP. Entropy 2021, 23, 1292. [Google Scholar] [CrossRef]
- Zhao, J.; Song, Y.; Deng, Y. A Novel Model to Identify the Influential Nodes: Evidence Theory Centrality. IEEE Access 2020, 8, 46773–46780. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A.; Jalili, M.; Fasaei, M.S.K. Finding influential nodes in social networks based on neighborhood correlation coefficient. Knowl.-Based Syst. 2020, 194, 105580. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, S.; Zhu, X. Information diffusion under public crisis in BA scale-free network based on SEIR model—Taking COVID-19 as an example. Phys. A Stat. Mech. Its Appl. 2021, 571, 125848. [Google Scholar] [CrossRef]
- Ullah, A.; Wang, B.; Sheng, J.; Long, J.; Khan, N.; Sun, Z. Identifying vital nodes from local and global perspectives in complex networks. Expert Syst. Appl. 2021, 186, 115778. [Google Scholar] [CrossRef]
- Ullah, A.; Wang, B.; Sheng, J.; Long, J.; Khan, N.; Gambuzza, L.V. Identification of Influential Nodes via Effective Distance-based Centrality Mechanism in Complex Networks. Complexity 2021, 2021, 8403738. [Google Scholar] [CrossRef]

| Network | |||||
|---|---|---|---|---|---|
| Football | 115 | 613 | 10.66 | 12 | 0.403 |
| Netscience | 379 | 914 | 4.823 | 34 | 0.741 |
| 1133 | 5451 | 9.622 | 71 | 0.202 | |
| Power | 4941 | 6594 | 2.669 | 19 | 0.080 |
| Network | Degree | BC | CC | LocalC | CLD | LWC |
|---|---|---|---|---|---|---|
| Football | 0.05 | 0.12 | 0.09 | 0.12 | 0.05 | 0.07 |
| Netscience | 0.11 | 0.84 | 0.28 | 0.14 | 0.09 | 0.17 |
| 0.39 | 8.12 | 2.92 | 0.26 | 0.45 | 0.52 | |
| Power | 0.57 | 115.32 | 38.92 | 0.88 | 0.76 | 1.39 |
| Network | M(Degree) | M(BC) | M(CC) | M(LocalC) | M(CLD) | M(LWC) |
|---|---|---|---|---|---|---|
| Football | 0.3637 | 1.0000 | 0.9488 | 0.9960 | 0.9915 | 1.0000 |
| Netscience | 0.7642 | 0.3390 | 0.9928 | 0.9887 | 0.9793 | 0.9944 |
| 0.8874 | 0.9400 | 0.9988 | 0.9981 | 0.9974 | 0.9997 | |
| Power | 0.5927 | 0.8319 | 0.9998 | 0.9014 | 0.9001 | 0.9653 |
| Network | Degree | BC | CC | LocalC | CLD | LWC |
|---|---|---|---|---|---|---|
| Football | 0.4089 | 0.2801 | 0.3516 | 0.4781 | 0.3603 | 0.4931 |
| Netscience | 0.2714 | 0.0116 | 0.1835 | 0.3826 | 0.4477 | 0.5048 |
| 0.6603 | 0.4755 | 0.5644 | 0.6482 | 0.7036 | 0.7217 | |
| Power | 0.3569 | 0.1916 | 0.3695 | 0.4959 | 0.5639 | 0.5670 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, Q.; Wu, L.; Zhang, J. Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy. Entropy 2022, 24, 293. https://doi.org/10.3390/e24020293
Zhang J, Zhang Q, Wu L, Zhang J. Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy. Entropy. 2022; 24(2):293. https://doi.org/10.3390/e24020293
Chicago/Turabian StyleZhang, Jinhua, Qishan Zhang, Ling Wu, and Jinxin Zhang. 2022. "Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy" Entropy 24, no. 2: 293. https://doi.org/10.3390/e24020293
APA StyleZhang, J., Zhang, Q., Wu, L., & Zhang, J. (2022). Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy. Entropy, 24(2), 293. https://doi.org/10.3390/e24020293






