1. Introduction
With the rapid development of the internet and computer technology, more images, videos, and other multimedia information are being transmitted and stored through the internet. Image information security is receiving more attention. Image encryption is an effective method to protect digital images [
1,
2,
3,
4,
5,
6].
Image encryption methods are currently available using various techniques, such as chaotic systems [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17], DNA coding [
18,
19,
20,
21], substitution boxes [
22,
23,
24], and cellular automata [
25,
26,
27,
28]. Chaotic phenomena [
29,
30] are seemingly random irregular motions that occur in a deterministic system—a system described by a deterministic theory that behaves in an uncertain, irreducible, and unpredictable manner. Chaotic systems are the most widely used and continuously improved systems in the field of image encryption. Chaotic systems for image encryption are classified into two categories: one-dimensional (1D) chaotic systems [
7,
8,
9,
10,
11] and multidimensional (MD) chaotic systems. One-dimensional chaotic systems have advantages, such as simple structures, easy implementation, and low computational complexity [
11], but they also have disadvantages, such as small key spaces and low security [
8,
9]. To solve this problem, some MD chaotic systems have been applied to image encryption [
12,
13,
14,
15,
16,
17]. The encryption algorithms based on MD systems have larger key spaces and higher security levels; however, MD chaotic systems are relatively difficult to implement in hardware or software and the respective encryption systems have high computational complexity [
11]. In this paper, we used Chebyshev mapping and logistic mapping to generate chaotic sequences for the encryption process and calculate the initial value of the one-dimensional chaotic system by the Secure Hash Algorithm-256(SHA-256) function, which is not only easy to implement and increase the key space, but it also reduces the computational complexity of the cryptosystem and improves the security of the algorithm.
As a revolutionary data acquisition technique, compressive sensing (CS) [
31,
32,
33] opens new perspectives for simultaneous compression and encryption of plaintexts, where the measurement matrix is shared between the sender and receiver as a key. To improve the confidentiality, linear feedback shift registers, pseudo-random number generators, and chaotic mappings were proposed to construct the measurement matrix [
34,
35,
36,
37,
38]. The design of the measurement matrix is the key to ensuring the quality of signal sampling and to determine the hardware implementation of compressed sampling.
The methods used for constructing the measurement matrix are divided into two categories. One is the random measurement matrix, which mainly includes Gaussian measurement matrix, Bernoulli measurement matrix, local Fourier measurement matrix, etc. [
32,
39]. Although these matrices can reconstruct the original signals well, they are difficult to implement in hardware, in practical applications; storing the matrix elements requires a large storage space. Another type of matrix is the deterministic measurement matrix. In constructing such a matrix, once the system parameters and the parameters of the construction are determined, the elements of the matrix are also determined. The chaotic sequence generated by the chaotic system is a unification of determinism and randomness, and the measurement matrix constructed from the chaotic sequence is a deterministic matrix, which can effectively solve the problems of instability and the need for multiple measurements in the common random measurement matrix in experiments. Therefore, some scholars proposed to use chaotic sequences for the construction of compressive–aware measurement matrices [
40,
41,
42,
43,
44]. L. Yu proposed using logistic chaotic sequences to construct measurement matrices in the literature [
40] and proved that the matrices satisfied the RIP condition; Frunzete [
41] et al. proved that the measurement matrices constructed by using tent chaotic sequences can satisfy the RIP condition. However, all of the above measurement matrix construction methods use chaotic sequences generated by a single chaotic mapping to construct the measurement matrix. The performance of the chaotic sequence generated by a single chaotic mapping is slightly worse than that of the hybrid chaotic sequence, so the performance of the measurement matrix is again influenced by the performance of the chaotic sequence [
43]. In order to avoid affecting the reconstruction effect of the signal due to the lack of performance of a single chaotic sequence, a measurement matrix construction algorithm based on the XOR operation chaotic sequence is proposed to improve the reconstruction performance of the measurement matrix and the easy implementation feature of the hardware.
To reduce the computational complexity and storage space, the block compressed sensing (BCS) framework was introduced to process medium to large images. R. Huang et al. [
45] designed a block cipher structure consisting of linear measurement, scrambling, S-box, and XOR operations. This scheme can work efficiently in the parallel computing environment. Zhu L et al. [
46] conducted a novel BCS-based encryption scheme. The nonuniform sampling strategy was adopted in BCS stage to improve the compression efficiency, and the permutation–diffusion framework was utilized to enhance security. Experiments show that the algorithm has good reconstruction capability, but it has low correlation with plaintext images, and is vulnerable to known plaintext and selected plaintext attacks.
In this paper, we propose a simple and secure image encryption algorithm based on BCS and one-dimensional chaotic mapping. This scheme is made up of two primary stages. In the first stage, after generating chaotic sequences using two simple one-dimensional chaotic mappings—a Chebyshev map and logistic map for binary quantization and XOR operations—a Bernoulli measurement matrix was generated and the measurement value matrix was obtained by performing BCS on the original image. In the second stage, still using the Chebyshev map and logistic map to generate chaotic sequences, the measurement value matrix was encrypted to obtain the ciphertext image. The simulation results verify the security, effectiveness, and good reconfiguration performance of the scheme. The main contributions of this paper are as follows.
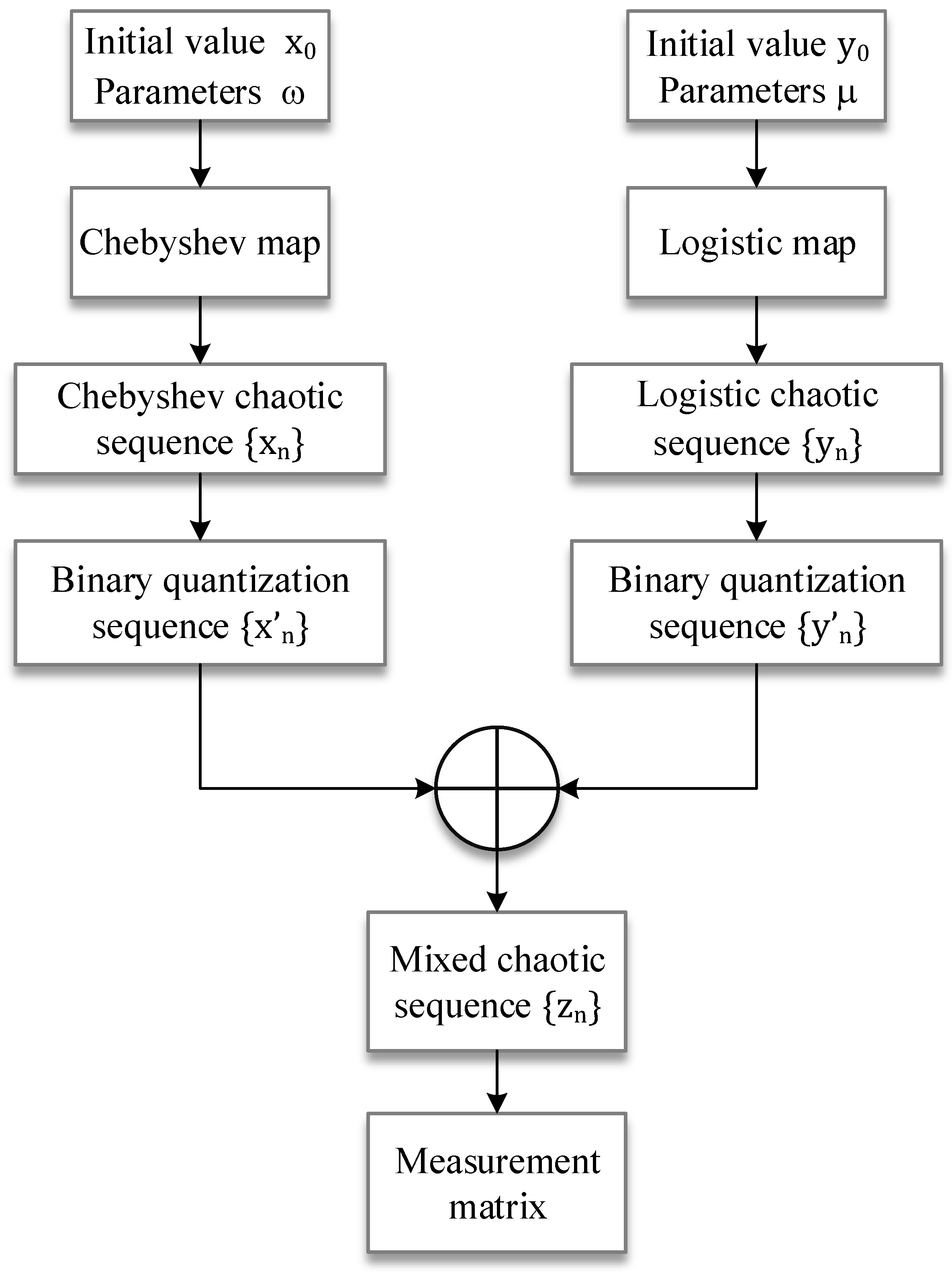
A hybrid chaotic sequence measurement matrix satisfying Bernoulli’s property based on Chebyshev map and a logistic map, which is easy to implement in hardware, is designed, and the performance of the resulting measurement matrix is analyzed and applied to BCS.
The SHA-256 value of the plaintext image is used to calculate the initial value of the chaotic mapping for the encryption algorithm part, which increases the relevance of the algorithm to the plaintext image and improves the ability of the scheme to resist the selective plaintext attack.
A “no repetition” scrambling algorithm and a Galois domain-based two-way diffusion algorithm are proposed to encrypt the measurement value matrix and improve the security of the BCS framework.
In the reconstruction stage, the SPL reconstruction algorithm, based on DDWT, is used, which, combined with the hybrid chaotic sequence measurement matrix proposed in this paper, can achieve a much higher reconstruction quality of decrypted images with low compression ratio.
The rest of this paper is organized as follows. The preliminaries are discussed in
Section 2. The proposed algorithm is described in
Section 3. Simulation results and discussion are given in
Section 4, and the statistical analysis of the scheme is discussed in
Section 5. Conclusions are given in
Section 6.
3. The Proposed Algorithm
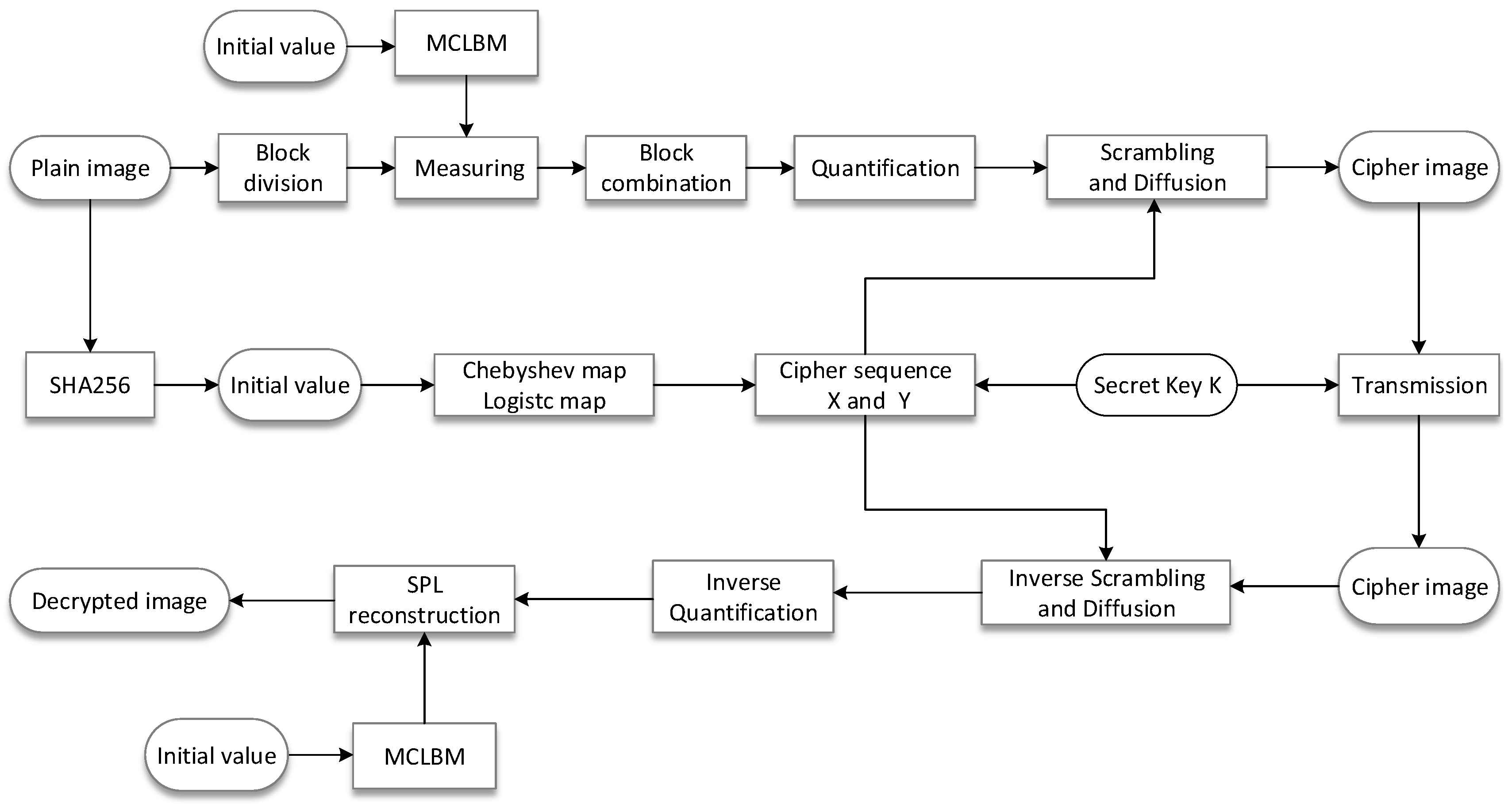
The main objective of the image compression/encryption algorithm proposed in this paper was to improve the performance of image compression, reconstruction, and encryption at low compression ratios; that is, with a reduced amount of more data. For this purpose, the plaintext images were blocked and measured using the MCLBM in the compressive measurement phase. To improve the resistance to selective plaintext attacks, the chaotic encryption sequence was generated for the plaintext image using the SHA-256 function to generate a key as the initial value of the chaotic map, and a new image encryption scheme was designed accordingly.
The proposed compression/encryption algorithm consists of two main processes, BCS compression sampling and quantization encryption of the measured values, as shown in
Figure 4. The specific steps are discussed in detail in the following sections.
3.1. Block Compression Sampling and Quantification Process
Assuming the BCS compression ratio is CR, the size of the plaintext image P is , and it is divided into non-overlapping blocks of size , which can be divided into blocks, and then these blocks are expanded into a one-dimensional vector in the scanning order from left to right and then from top to bottom, and noted as . The BCS compression sampling process is as follows:
Generate the MCLB sequence
, from the steps in
Section 2.2.2, and
,
,
.
Generate a measurement matrix
of size
by cyclically shifting
by columns:
Express
as a row vector as
. Let
and use Equations (16) and (17) to normalize the row vectors.
where
denotes the inner product of vector
and
, and
denotes the 2-norm of vector
. Finally, measurement matrix
after orthogonal normalization is obtained.
Compress the plaintext image
P after blocked and obtain the measurement value
of each block.
Finally,
is combined in blocks to obtain the measurement value matrix
C, at which point the measurement value matrix is
At this time, the size of is , and the data are obviously smaller than that of the original image. If the compression ratio is CR = 0.25, then the size of is only 1/4 of the size of the plaintext image, which is convenient for the subsequent encryption processing.
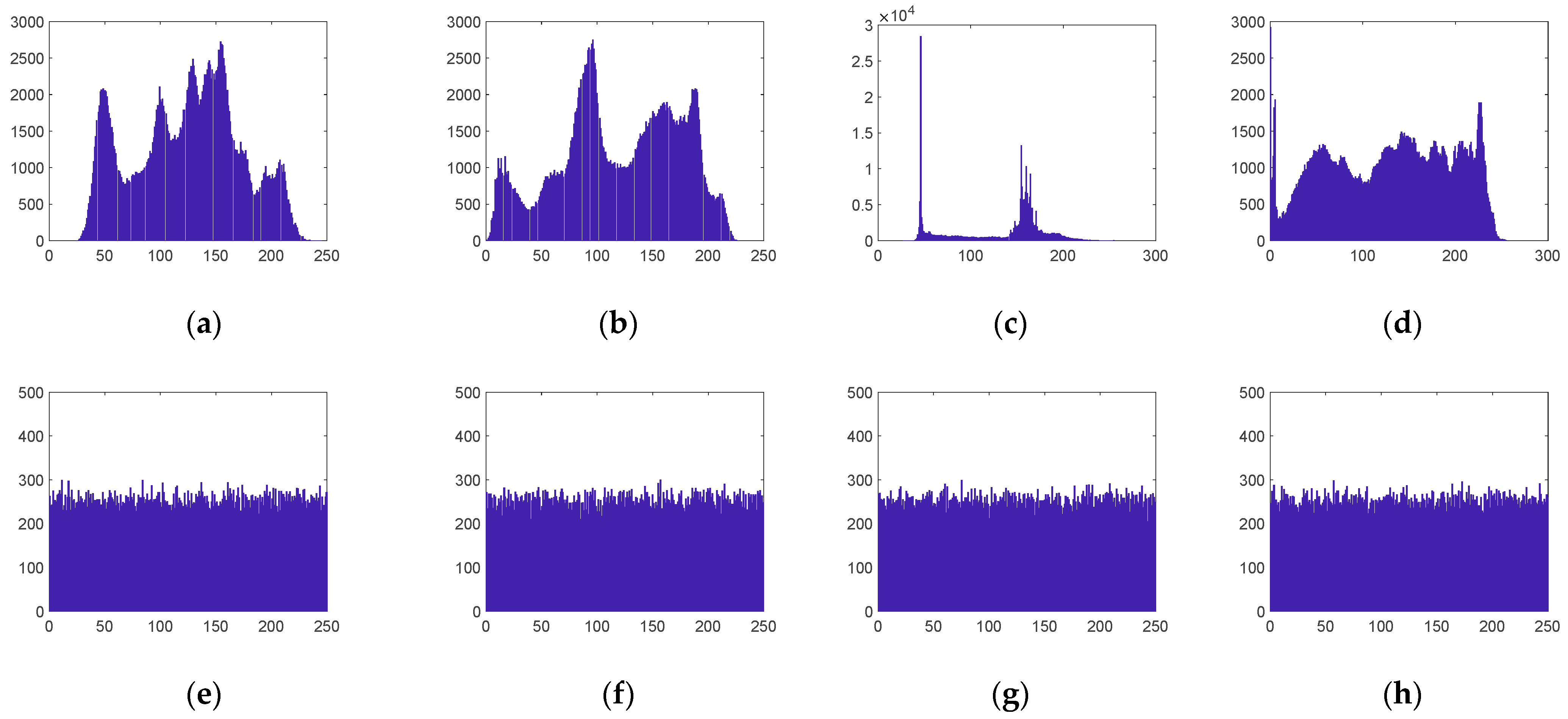
The output matrix values after CS measurements are usually outside the grayscale range of [0, 255]. Therefore, it must be quantized before encryption. The quantization process is expressed as follows:
where
represents the maximum integer value that is not greater than
and min and max are the minimum and maximum elements of the measurement matrix
, respectively.
3.2. Cipher Sequence Generation Algorithm
In order to make the proposed encryption algorithm resistant to known plaintext and selected plaintext attacks, this paper uses the SHA-256 value of the plaintext image to calculate the parameters and initial values of the variable parameter chaotic mapping, so that the parameters and initial values are closely related to the plaintext image. The specific steps are as follows.
The 256-bit hash of the plaintext image is first obtained, written in 64-bit hexadecimal form, and then each bit is converted to the corresponding decimal number, which is used as the key K and is denoted as:
where
. The encryption algorithm requires the use of Chebyshev chaotic map and the logistic chaotic map to generate two cipher sequences, so generate their initial values
,
,
, and
according to the key
, generated by the following equation.
Then the initial values
,
,
, and
generated by SHA-256 are substituted into Equations (4) and (6) to generate a chaotic sequence
and a chaotic sequence
, respectively, after which the elemental values of the chaotic sequences
and
are quantized using the following equation:
Sequence is used for scrambling and for diffusion.
3.3. Image Encryption Algorithm
The encryption process begins with a scrambling of the matrix of measurement values, followed by a diffusion operation, as follows.
First, keep only one of the recurring pseudo-random numbers in the pseudo-random sequence (i.e., the first occurrence), then add the values in that do not appear in to the end of in descending order, and note . is then used to displace without repetition. is then expanded column-wise into a one-dimensional vector, denoted . Finally, is swapped with to give the disordered matrix .
Select the first
values of the sequence
to form the sequence
.
is obtained by forward diffusion of
using
as follows.
where “
” represents the multiplication operation of GF(257) domain and
.
Select the values from
to
of the sequence
to form the sequence
. Use
to perform backward diffusion on
to obtain
, as follows.
where “
” represents the multiplication operation of GF(257) domain and
.
Finally, is rearranged into a matrix of by columns, and after the above operation, the ciphertext image is obtained.
3.4. Image Decryption and Reconstruction Process
The decompression and decryption process is the opposite of the compression and encryption process. The steps are summarized as follows:
Use the key K to generate the chaotic mapping initial values , , , and , and generate and by Equation (23).
The received ciphertext image is sequentially subjected to backward diffusion, forward diffusion, and scrambling algorithms to obtain the quantized measurement value matrix .
The measurement matrix
is recovered by inverse quantization of the quantized measurement matrix
by the following equation:
The parameters and the initial value of the MCLB transmitted by the sender are used to iterate and generate the MCLBM, that is, the measurement matrix .
The DDWT-SPL algorithm is used to reconstruct the recovered measurement matrix to obtain a reconstructed original image of size .
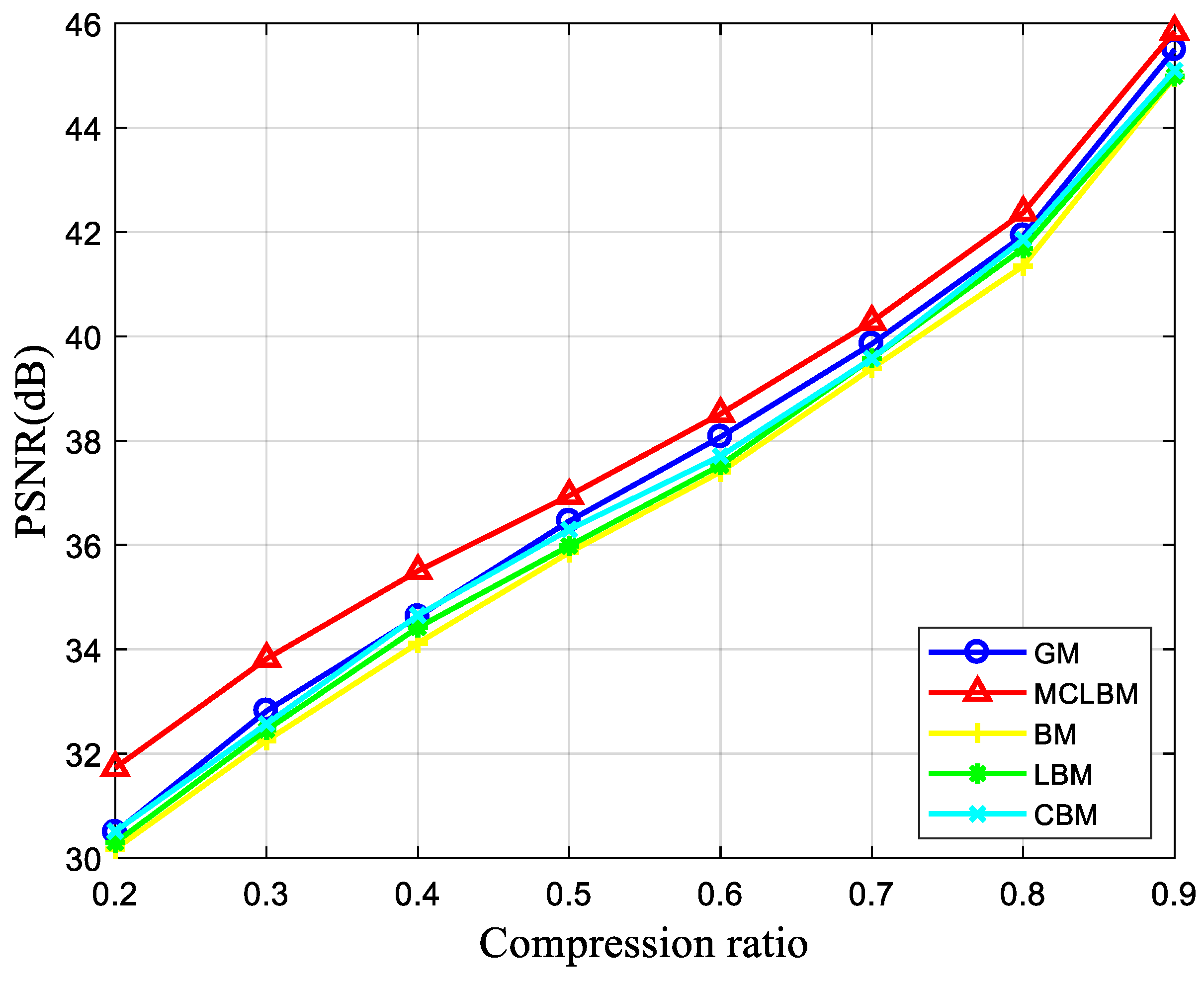
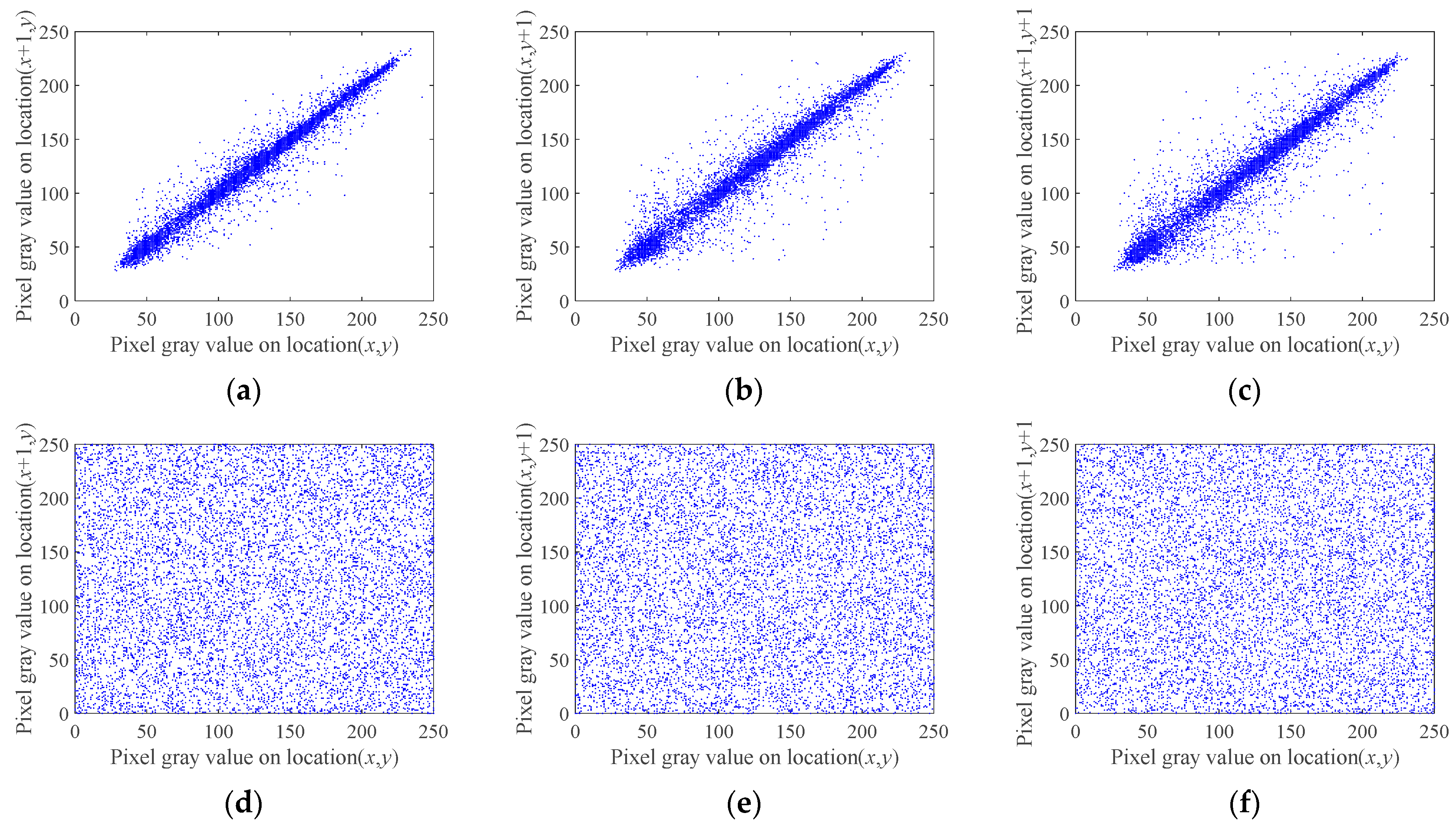
6. Conclusions
A block compressive sensing image encryption algorithm based on the mixed chaotic Bernoulli measurement matrix is proposed. The core of this encryption algorithm is the combination of the mixed chaotic sequence measurement matrix and BCS, which is practical and can improve the reconstruction quality of images with low compression ratios under the premise of ensuring system security and easy hardware implementation. The compression performance of the mixed chaotic sequence measurement matrix was analyzed, and the performance analysis shows that the measurement matrix has better measurement reconstruction performance than the ordinary measurement matrix. In the encryption process, the SHA-256 function of the plaintext image was used to generate the initial values of the desired chaotic sequence, which improved the ability of the scheme to resist the selective plaintext attack. Finally, the results of the encryption scheme were analyzed and evaluated. First, the effect of reconstructing the image was analyzed; the method has better reconstruction capabilities at a low compression ratio compared with other methods, which could greatly reduce the amount of data to be processed. Secondly, the security of the encryption algorithm was analyzed. The encryption algorithm could resist various attacks from key space, statistical analysis, and information entropy. Finally, the proposed encryption scheme has good encryption effects and image compression capabilities.