Plasma-like Description for Elementary and Composite Quantum Particles
Abstract
1. Introduction
- How can a continuous charge density distribution be approximated by a discrete one with a quantized charge?
- What mathematical model (equations of motion) can underlie such a description?
- How can the description be extended to composite particles?
- What are some implications of the obvious analogy with plasma?
2. Methods and Results
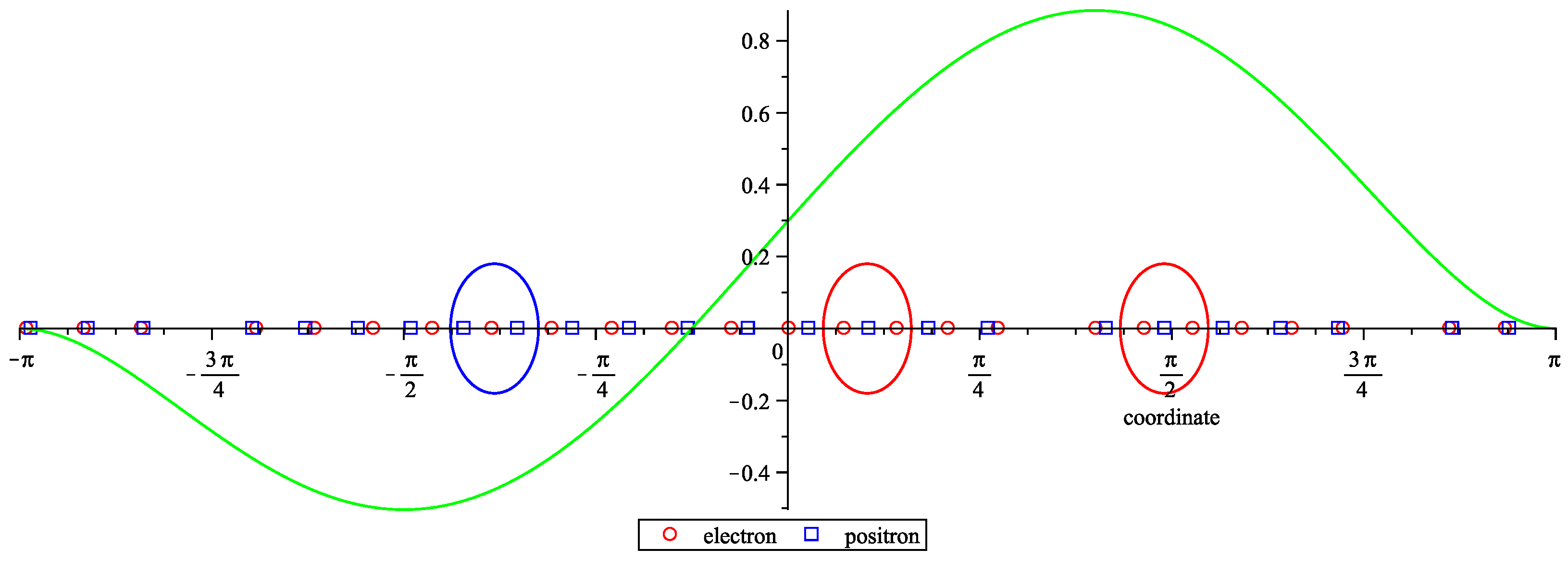
2.1. Approximation of a Continuous Charge Density Distribution by a Discrete One with a Quantized Charge
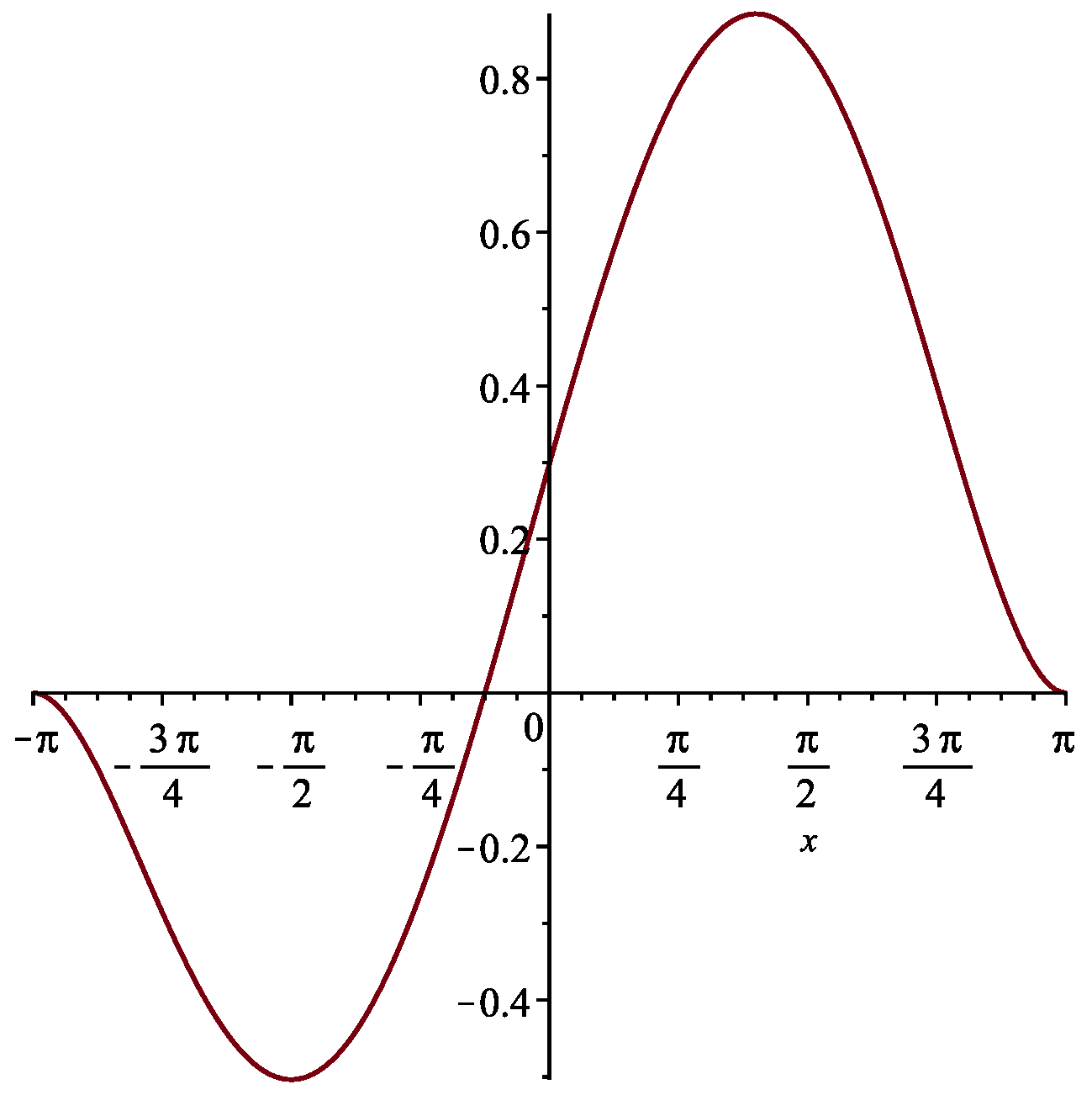
2.2. An Example Mathematical Model
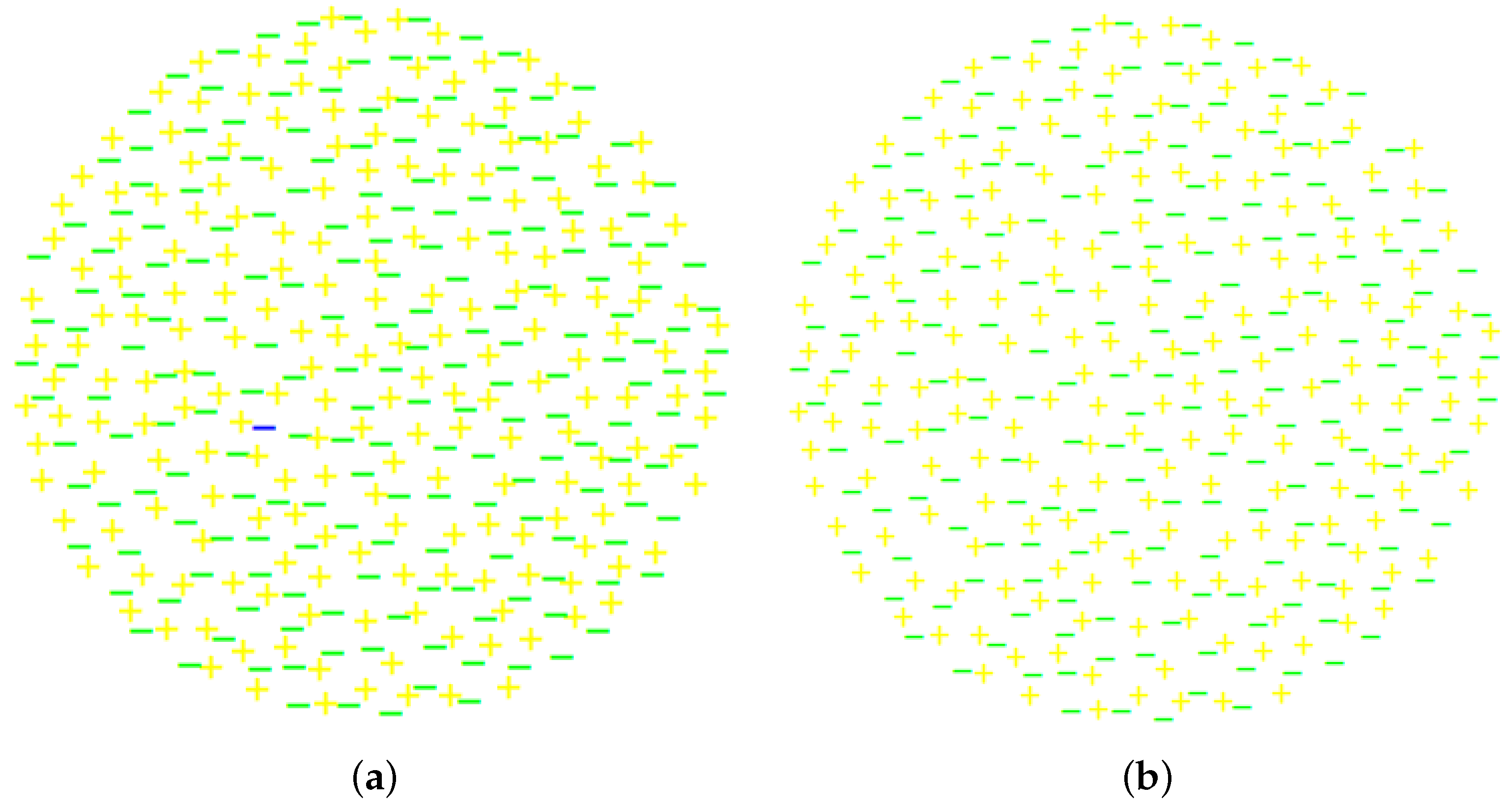
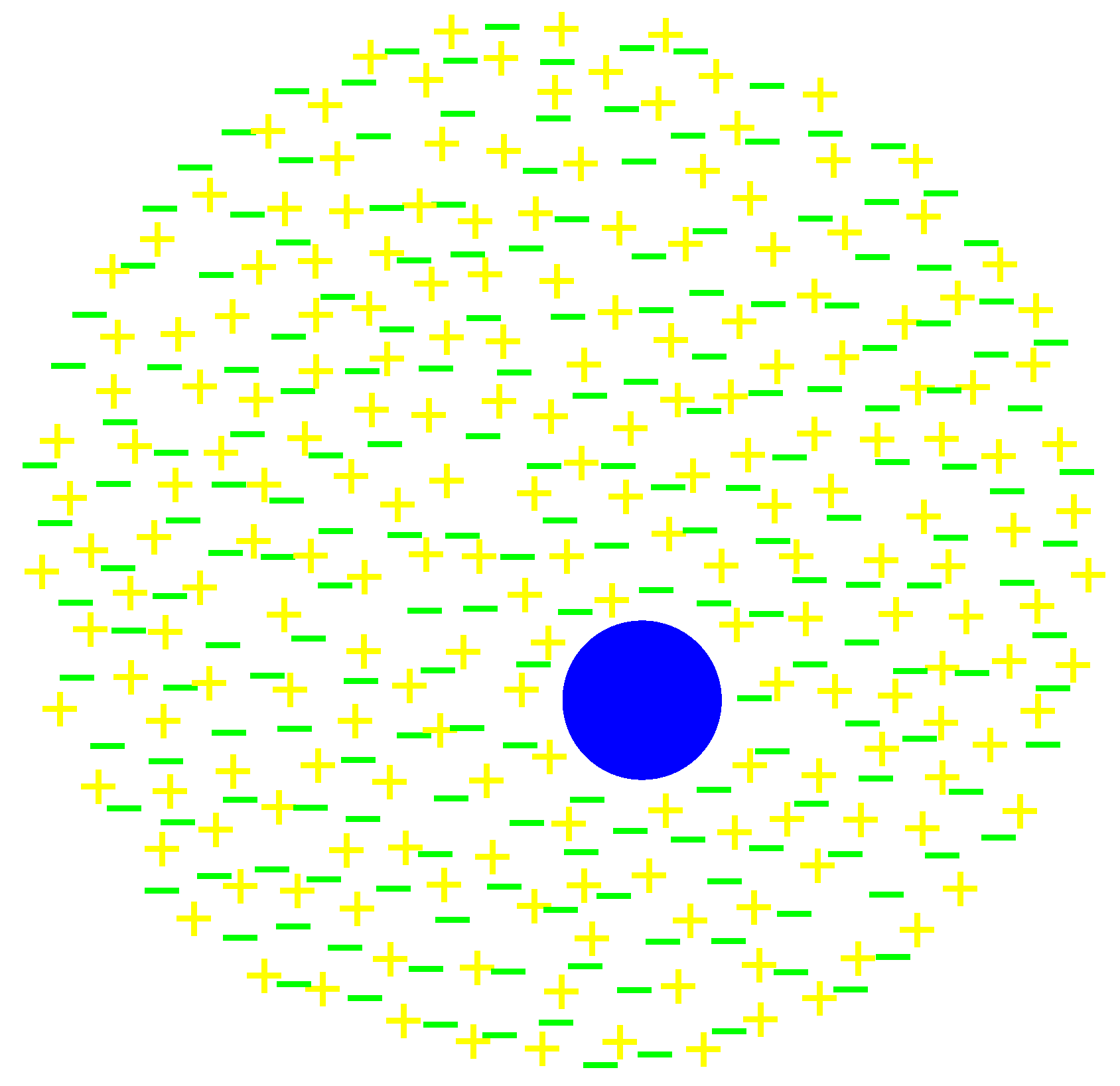
2.3. Extension to Composite Particles
2.4. The Plasma Analogy
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Electron Coordinates | Positron Coordinates |
| −3.1126741447007592777837555796944 | 2.9530344365605025711769473845442 |
| −2.8775683647214638678316386267493 | −3.0951381769952591512118001250174 |
| −2.6434375832598523581831400447478 | −2.8614098696120820985572576736353 |
| −1.9336327385447378036758712466442 | −2.1882892356297157247876068745650 |
| −1.6936070421273554090248068336325 | −2.6326516523345556425794778026752 |
| −2.1719682464297679903185420586677 | −1.9710273543645197236521756279888 |
| −1.4519956803651471460404417607211 | −1.7555235230550466106754786539860 |
| −1.2088029171600329445514113518049 | −1.5403236844404032536985003739319 |
| −0.96395311532928105718506480243987 | −1.1039117628153018022432733933447 |
| −0.71762228955760307445232301075533 | −1.3237515410575950384914085327471 |
| −0.47125651467198634491476595790667 | −0.87873421856160715534322966231588 |
| −0.22858211104030609796912348102868 | −0.64632138885302414208246702251485 |
| 0.86186952364267439824952086701953 | 0.33294945631962504080286722164668 |
| 0.00616783249506095738298247885632 | −0.40611981918357315216289810648891 |
| 0.23137130395092737580909635004611 | −0.16042959567225122871033380542859 |
| 0.44789490782808160879397312969880 | 0.08676186721721802846687332761214 |
| 0.65746934747098210872577876522952 | 0.57756516301030844804631542526482 |
| 1.2615668189213491342215825540197 | 0.82076073717919350910333838443007 |
| 1.4597980397241581466451663147530 | 1.3035691589932125510920278727478 |
| 2.0643955075009215796102922944881 | 2.0187559332910846063814218989366 |
| 1.6587989484672624969753714473643 | 1.7817077278249609050042692119912 |
| 1.8599046587703446165936780433590 | 1.5432590795101890022517254564541 |
| 2.2734402898434140647729061709433 | 2.2542171585208840682836715659146 |
| 2.7088031793185310430667064345281 | 2.7204794077160776393522523646147 |
| 2.9363544347316877716974068736781 |
References
- Schlosshauer, M.; Kofler, J.; Zeilinger, A. A snapshot of foundational attitudes toward quantum mechanics. Stud. Hist. Philos. Mod. Phys. 2013, 44, 222. [Google Scholar] [CrossRef]
- Sommer, C. Another survey of foundational attitudes towards quantum mechanics. arXiv 2013, arXiv:1303.2719. [Google Scholar]
- Norsen, T.; Nelson, S. Yet another snapshot of foundational attitudes toward quantum mechanics. arXiv 2013, arXiv:1306.4646. [Google Scholar]
- Sivasundaram, S.; Nielsen, K.H. Surveying the attitudes of physicists concerning foundational issues of quantum mechanics. arXiv 2016, arXiv:1612.00676. [Google Scholar]
- Craver, C.; Tabery, J. Available online: https://plato.stanford.edu/entries/science-mechanisms/ (accessed on 28 November 2021).
- Sanz, A.S. Bohm’s approach to quantum mechanics: Alternative theory or practical picture? Front. Phys. 2019, 14, 11301. [Google Scholar] [CrossRef]
- Schrödinger, E. Dirac’s New Electrodynamics. Nature 1952, 169, 538. [Google Scholar] [CrossRef]
- Akhmeteli, A. One real function instead of the Dirac spinor function. J. Math. Phys. 2011, 52, 082303. [Google Scholar] [CrossRef]
- Akhmeteli, A. The Dirac Equation as One Fourth-Order Equation for One Function: A General, Manifestly Covariant Form. arXiv 2015, arXiv:1502.02351. [Google Scholar]
- Akhmeteli, A. The Dirac Equation as One Fourth-Order Equation for One Function: A General, Manifestly Covariant Form. In Quantum Foundations, Probability and Information; Khrennikov, A., Bourama, T., Eds.; Springer: Cham, Switzerland, 2018; p. 1. [Google Scholar]
- Bagrov, V.G.; Gitman, D. The Dirac Equation and its Solutions; Walter de Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2014. [Google Scholar]
- Bagrov, V.G. Squaring the Dirac Equations. Russ. Phys. J. 2018, 61, 403. [Google Scholar] [CrossRef]
- Akhmeteli, A. The Dirac equation in a Yang-Mills field as an equation for just one real function. arXiv 2018, arXiv:1811.02441. [Google Scholar]
- Akhmeteli, A.M. Real-Valued Charged Fields and Interpretation of Quantum Mechanics. arXiv 2005, arXiv:quant-ph/0509044. [Google Scholar]
- Akhmeteli, A. No drama quantum electrodynamics? Eur. Phys. J. C 2013, 73, 2371. [Google Scholar] [CrossRef][Green Version]
- Khrennikov, A. Is the Devil in h? Entropy 2021, 23, 632. [Google Scholar] [CrossRef] [PubMed]
- Colin, S.; Durt, T.; Willox, R. de Broglie’s double solution program: 90 years later. Ann. Fond. Louis Broglie 2017, 42, 19. [Google Scholar]
- Vigier, J.P. Evidence For Nonzero Mass Photons Associated with a Vacuum-Induced Dissipative Red-Shift Mechanism. IEEE Trans. Plasma Sci. 1990, 18, 64. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J. The quest for the quark-gluon plasma. Nature 2007, 448, 302. [Google Scholar] [CrossRef] [PubMed]
- Schlosshauer, M. Experimental motivation and empirical consistency in minimal no-collapse quantum mechanics. Ann. Phys. 2006, 321, 112. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Understanding quantum measurement from the solution of dynamical models. Phys. Rep. 2013, 525, 1. [Google Scholar] [CrossRef]
- Strassler, M. Available online: https://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-structure-of-matter/protons-and-neutrons/ (accessed on 29 November 2021).
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An ontological basis for the quantum theory. Phys. Rep. 1987, 144, 321. [Google Scholar] [CrossRef]
- Vedral, V. A Classical (Local) Account of The Aharonov-Bohm Effect. arXiv 2021, arXiv:2111.00476. [Google Scholar]
- Akhmeteli, A. Is no drama quantum theory possible? Int. J. Quantum Inf. 2011, 9, 17–26. [Google Scholar] [CrossRef]
- Kowalski, K.; Steeb, W.H. Nonlinear Dynamical Systems and Carleman Linearization; World Scientific: Singapore, 1991. [Google Scholar]
- Kowalski, K. Methods of Hilbert Spaces in the Theory of Nonlinear Dynamical Systems; World Scientific: Singapore, 1994. [Google Scholar]
- Georgi, H. Effective Field Theory. Annu. Rev. Nucl. Part. Sci. 1993, 43, 209. [Google Scholar] [CrossRef]
- Verschelde, J. Algorithm 795: PHCpack: A General-Purpose Solver for Polynomial Systems byHomotopy Continuation. ACM Trans. Math. Softw. 1999, 25, 251. [Google Scholar] [CrossRef]
- Leykin, A. Available online: https://antonleykin.math.gatech.edu/math4803spr13/BOOK/chapter2.pdf (accessed on 29 November 2021).
- Verschelde, J. Available online: http://homepages.math.uic.edu/~jan/download.html (accessed on 29 November 2021).
- Lee, H.W. Theory and application of the quantum phase-space distribution functions. Phys. Rep. 1995, 259, 147. [Google Scholar] [CrossRef]
- Sebens, C.T. Electron Charge Density: A Clue from Quantum Chemistry for Quantum Foundations. Found. Phys. 2021, 51, 75. [Google Scholar] [CrossRef]
- Barut, A.O. Combining Relativity and Quantum Mechanics: Schrödinger’s Interpretation of ψ. Found. Phys. 1988, 18, 95–105. [Google Scholar] [CrossRef]
- Khrennikov, A. Beyond Quantum; Pan Stanford Publishing: Singapore, 2014. [Google Scholar]
- Nikolić, H. Bohmian Particle Trajectories in Relativistic Bosonic Quantum Field Theory. Found. Phys. Lett. 2004, 17, 363. [Google Scholar] [CrossRef]
- Horton, G.; Dewdney, C.; Nesteruk, A. Time-like flows of energy momentum and particle trajectories for the Klein-Gordon equation. J. Phys. 2000, A33, 7337. [Google Scholar] [CrossRef]
- Tumulka, R. Response to Horton and Dewdney. arXiv 2002, arXiv:quant-ph/0210018. [Google Scholar]
- Holland, P.R. The Quantum Theory of Motion; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Zeilinger, A.; Gähler, R.; Shull, C.G.; Treimer, W.; Mampe, W. Single- and double-slit diffraction of neutrons. Rev. Mod. Phys. 1988, 60, 1067. [Google Scholar] [CrossRef]
- Fein, Y.Y.; Geyer, P.; Zwick, P.; Kiałka, F.; Pedalino, S.; Mayor, M.; Gerlich, S.; Arndt, M. Quantum superposition of molecules beyond 25 kDa. Nat. Phys. 2019, 15, 1242. [Google Scholar] [CrossRef]
- Duane, W. The Transfer in Quanta of Radiation Momentum to Matter. Proc. Natl. Acad. Sci. USA 1923, 9, 158. [Google Scholar] [CrossRef] [PubMed]
- Epstein, P.S.; Ehrenfest, P. The Quantum Theory of the Fraunhofer Diffraction. Proc. Natl. Acad. Sci. USA 1924, 10, 133. [Google Scholar] [CrossRef] [PubMed]
- Landé, A. Why Do Quantum Theorists Ignore the Quantum Theory? Br. J. Philos. Sci. 1965, XV, 307. [Google Scholar] [CrossRef]
- Couder, Y.; Fort, E. Single-Particle Diffraction and Interference at a Macroscopic Scale. Phys. Rev. Lett. 2006, 97, 154101. [Google Scholar] [CrossRef]
- Plyukhin, A.V.; Schofield, J. Stochastic model related to the Klein-Gordon equation. Phys. Rev. E 2001, 64, 037101. [Google Scholar] [CrossRef]
- Shi, Y.; Fisch, N.J.; Qin, H. Effective-action approach to wave propagation in scalar QED plasmas. Phys. Rev. A 2016, 94, 012124. [Google Scholar] [CrossRef]
- Stenson, E.V.; Horn-Stanja, J.; Stoneking, M.R.; Pedersen, T.S. Debye length and plasma skin depth: Two length scales of interest in the creation and diagnosis of laboratory pair plasmas. J. Plasma Phys. 2017, 83, 595830106. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Principles of Quantum Mechanics, 4th ed.; Oxford University Press: Oxford, UK, 1958; p. 263. [Google Scholar]
- Thaller, B. The Dirac Equation; Springer: Berlin/Heidelberg, Germany, 1992; p. 18. [Google Scholar]
- Catillon, P.; Cue, N.; Gaillard, M.; Genre, R.; Gouanère, M.; Kirsch, R.; Poizat, J.C.; Remillieux, J.; Roussel, L.; Spighel, M. A Search for the de Broglie Particle Internal Clock by Means of Electron Channeling. Found. Phys. 2008, 38, 659. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhmeteli, A. Plasma-like Description for Elementary and Composite Quantum Particles. Entropy 2022, 24, 261. https://doi.org/10.3390/e24020261
Akhmeteli A. Plasma-like Description for Elementary and Composite Quantum Particles. Entropy. 2022; 24(2):261. https://doi.org/10.3390/e24020261
Chicago/Turabian StyleAkhmeteli, Andrey. 2022. "Plasma-like Description for Elementary and Composite Quantum Particles" Entropy 24, no. 2: 261. https://doi.org/10.3390/e24020261
APA StyleAkhmeteli, A. (2022). Plasma-like Description for Elementary and Composite Quantum Particles. Entropy, 24(2), 261. https://doi.org/10.3390/e24020261





