Possibility and Time in Quantum Mechanics
Abstract
:1. Introduction
2. Modality in Quantum Mechanics
2.1. The Different Forms of Possibility
2.2. Actualism Versus Possibilism
2.3. Possibility, Probability, and Interpretation of Quantum Mechanics
3. Two Notions of Time in Quantum Mechanics
3.1. The Obstacle to an Observable Time
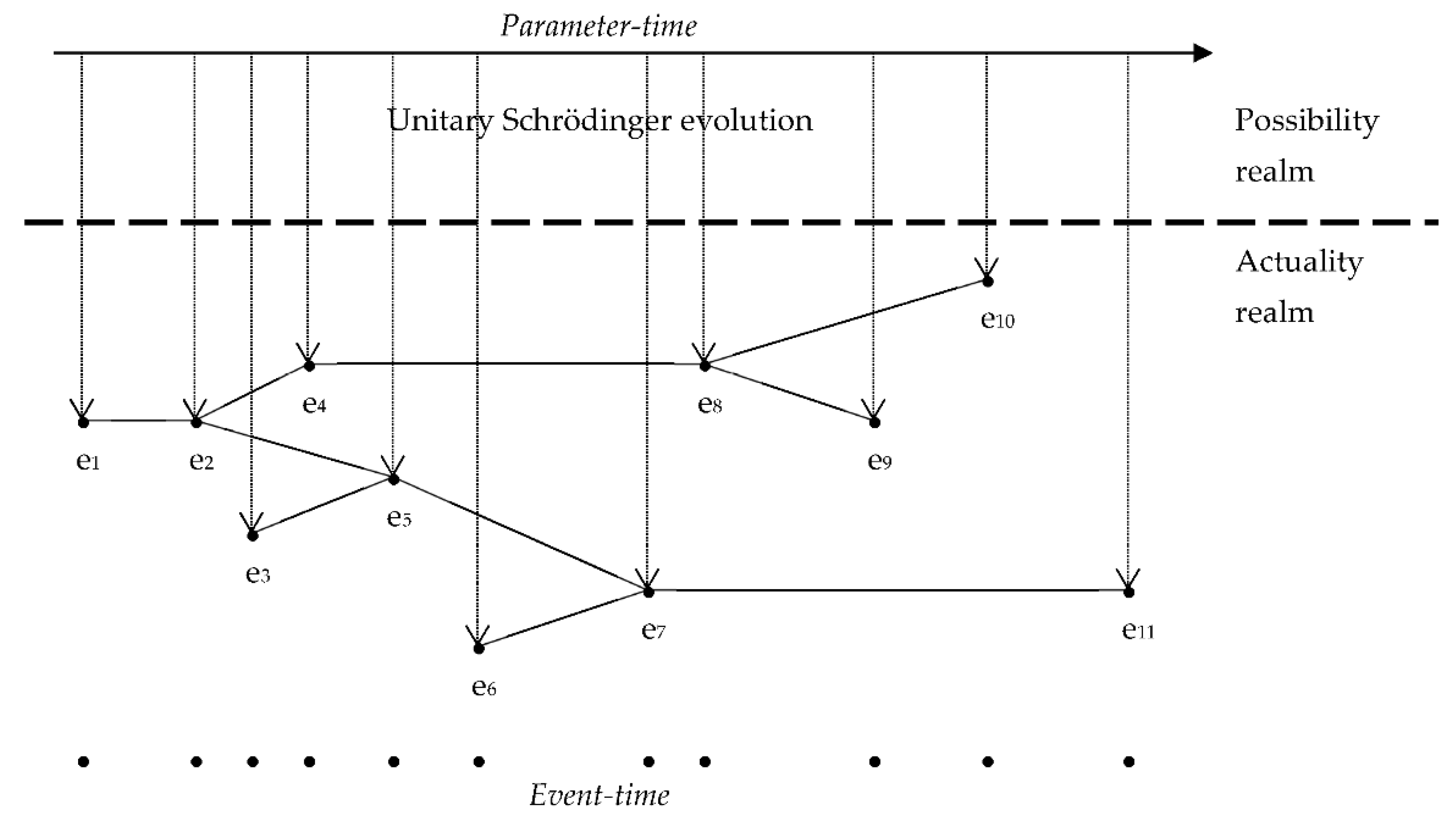
3.2. Parameter-Time and Event-Time
- -
- The parameter-time is the time over which the system’s state unitarily evolves. It is represented by the variable t as it appears in the Schrödinger equation.
- -
- The event-time (also called ‘observable’ time by Paul Busch [42]) is the time at which particular events occur. Those events are measurement results or, more generally, any acquisition of a definite value by a certain observable.
4. The Link between Possibility and Time
4.1. Possibility and Parameter-Time
4.2. Actuality and Event-Time
5. Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Kment, B. Varieties of modality. In The Stanford Encyclopedia of Philosophy, Spring 2017 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/spr2021/entries/modality-varieties (accessed on 20 December 2021).
- Knuuttila, S. Medieval theories of modality. In The Stanford Encyclopedia of Philosophy, Summer 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/sum2021/entries/modality-medieval (accessed on 20 December 2021).
- Lagerlund, H. Medieval theories of the syllogism. In The Stanford Encyclopedia of Philosophy, Summer 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/sum2021/entries/medieval-syllogism (accessed on 20 December 2021).
- Bunge, M. Treatise on Basic Philosophy, Vol.3: Ontology I; Reidel Publishing Company: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Quine, W.V.O. Word and Object; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Quine, W.V.O. On what there is. In From a Logical Point of View; Harper: New York, NY, USA, 1953; pp. 1–19. [Google Scholar]
- Montague, R. Logical necessity, physical necessity, ethics and quantifiers. Inquiry 1960, 3, 259–269, Reprinted in Formal Philosophy. Selected Papers of Richard Montague; Yale University Press: Thomason, NH, USA, 1974. [Google Scholar] [CrossRef]
- Øhrstrøm, P.; Hasle, P. Future contingents. In The Stanford Encyclopedia of Philosophy, Summer 2020 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2020; Available online: https://plato.stanford.edu/archives/sum2021/entries/future-contingents (accessed on 20 December 2021).
- Menzel, C. Actualism. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/fall2021/entries/actualism (accessed on 20 December 2021).
- Kneale, W.; Kneale, M. The Development of Logic; Clarendon Press: Oxford, UK, 1962. [Google Scholar]
- Prior, A. Past, Present and Future; Clarendon Press: Oxford, UK, 1967. [Google Scholar]
- Russell, B. Introduction to Mathematical Philosophy; George Allen and Unwin: London, UK, 1919. [Google Scholar]
- Bobzien, S. Dialectical school. In The Stanford Encyclopedia of Philosophy, Spring 2019 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2011; Available online: https://plato.stanford.edu/entries/dialectical-school (accessed on 20 December 2021).
- Gould, J.B. The Philosophy of Chrysippus; Suny Press: Albany, NY, USA, 1970. [Google Scholar]
- James, W. The dilemma of determinism. In The Will to Believe; Dover Publications: New York, NY, USA, 1896. [Google Scholar]
- Popper, K. The Open Universe: An Argument for Indeterminism; Hutchinson: London, UK, 1982. [Google Scholar]
- Russell, B. On the notion of cause with applications to the free-will problem. In Readings in the Philosophy of Science; Feigl, H., Brodbeck, G., Eds.; Appleton: New York, NY, USA, 1953; pp. 387–418. [Google Scholar]
- Lewis, D. Philosophical Papers; Oxford University Press: Oxford, UK, 1986; Volume 2. [Google Scholar]
- Lewis, D. Humean supervenience debugged. Mind 1994, 103, 473–490. [Google Scholar] [CrossRef]
- Maudlin, T. The Metaphysics Within Physics; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Hacking, I. The Emergence of Probability; Cambridge University Press: Cambridge, UK, 1975. [Google Scholar]
- Hájek, A. Interpretations of probability. In The Stanford Encyclopedia of Philosophy, Fall 2019 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2019; Available online: https://plato.stanford.edu/archives/spr2019/entries/probability-interpret (accessed on 20 December 2021).
- Keynes, J.M. A Treatise on Probability; Macmillan: London, UK, 1921. [Google Scholar]
- Carnap, R. Logical Foundation of Probability, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 1962. [Google Scholar]
- Ramsey, F.P. Truth and probability. In The Foundations of Mathematics and other Logical Essays; Braithwaite, R.B., Ed.; Routledge and Kegan Paul: London, UK, 1931; pp. 156–198. [Google Scholar]
- de Finetti, B. La prévision: Ses lois logiques, ses sources subjectives. Ann. De L’institut Henri Poincaré 1937, 7, 1–68. [Google Scholar]
- Reichenbach, H. The Theory of Probability; University of California Press: Berkeley, CA, USA, 1949. [Google Scholar]
- von Mises, R. Probability, Statistics and Truth; Macmillan: New York, NY, USA, 1957. [Google Scholar]
- Popper, K. The propensity interpretation of probability. Br. J. Philos. Sci. 1959, 10, 25–42. [Google Scholar] [CrossRef]
- Howard, D. Who invented the “Copenhagen Interpretation”? A study in mythology. Philos. Sci. 2004, 71, 669–682. [Google Scholar] [CrossRef]
- Goldstein, S. Bohmian mechanics. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/fall2021/entries/qm-bohm (accessed on 20 December 2021).
- Tumulka, R. Bohmian mechanics. In The Routledge Companion to the Philosophy of Physics; Knox, E., Wilson, A., Eds.; Routledge: Abingdon, UK, 2020. [Google Scholar]
- Wallace, D. The Emergent Multiverse: Quantum Theory according to the Everett Interpretation; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Vaidman, L. Many-worlds interpretation of quantum mechanics. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/fall2021/entries/qm-manyworlds (accessed on 20 December 2021).
- Caves, C.; Fuchs, C.; Schack, R. Quantum probabilities as Bayesian probabilities. Phys. Rev. A 2002, 65, 022305. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, C.; Mermin, D.; Schack, R. An introduction to QBism with an application to the locality of quantum mechanics. Am. J. Phys. 2014, 82, 749–754. [Google Scholar] [CrossRef] [Green Version]
- Albert, D. Elementary quantum metaphysics. In Bohmian Mechanics and Quantum Mechanics: An Appraisal; Cushing, J.T., Fine, A., Goldstein, S., Eds.; Kluwer: Dordrecht, The Netherlands, 1996; pp. 277–284. [Google Scholar]
- Ney, A. Ontological reduction and the wave function ontology. In The Wave Function. Essays on the Metaphysics of Quantum Mechanics; Ney, A., Albert, D., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 168–183. [Google Scholar]
- Heisenberg, W. Ueber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Für Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Bohr, N. Das Quantenpostulat und die neuere Entwicklung der Atomistik. Naturwissenschaften 1928, 16, 245–257. [Google Scholar] [CrossRef]
- Busch, P. On the energy-time uncertainty relation. Part I: Dynamical time and time indeterminacy. Found. Phys. 1990, 20, 1–32. [Google Scholar] [CrossRef]
- Busch, P. The time-energy uncertainty relation. In Time in Quantum Mechanics; Muga, J., Mayato, R.S., Egusquiza, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 734, pp. 73–105. [Google Scholar]
- Butterfield, J. On time in quantum physics. In A Companion to the Philosophy of Time; Dyke, H., Bardon, A., Eds.; Wiley-Blackwell: West Sussex, UK, 2013; pp. 220–241. [Google Scholar]
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 1932. [Google Scholar]
- Ballentine, L. Quantum Mechanics; A Modern Development; World Scientific: Singapore, 1989. [Google Scholar]
- Pauli, W. Die Allgemeinen Prinzipien der Wellenmechanik. In Handbuch der Physik, 2nd ed.; Geiger, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1933; Volume 24, pp. 83–272. [Google Scholar]
- Mandelstam, L.; Tamm, I. The uncertainty relation between energy and time in non-relativistic quantum mechanics. J. Phys. (USSR) 1945, 9, 249–254. [Google Scholar]
- Hilgevoord, J.; Uffink, J. The mathematical expression of the uncertainty principle. In Microphysical Reality and Quantum Formalism; van der Merwe, A., Selleri, F., Tarozzi, G., Eds.; Kluwer: Dordrecht, The Netherlands, 2016; pp. 91–114. [Google Scholar]
- Uffnk, J.; Hilgevoord, J. Uncertainty principle and uncertainty relations. Found. Phys. 1985, 15, 925–944. [Google Scholar] [CrossRef]
- Rovelli, C. Is there incompatibility between the ways time is treated in general relativity and in standard quantum mechanics? In Conceptual Problems of Quantum Gravity; Ashtekar, A., Stachel, J., Eds.; Birkhauser: New York, NY, USA, 1991; pp. 126–136. [Google Scholar]
- Busch, P. On the energy-time uncertainty relation. Part II: Pragmatic time versus energy Indeterminacy. Found. Phys. 1990, 20, 33–43. [Google Scholar] [CrossRef]
- Isham, C.J. Canonical quantum gravity and the problem of time. In Integrable Systems, Quantum Groups, and Quantum Field Theories; Ibort, L.A., Rodríguez, M.A., Eds.; NATO ASI Series (Series C: Mathematical and Physical Sciences); Springer: Dordrecht, The Netherlands, 1993; Volume 409, pp. 157–287. [Google Scholar]
- Kuchař, K. The problem of time in canonical quantization. In Conceptual Problems of Quantum Gravity; Ashtekar, A., Stachel, J., Eds.; Birkhäuser: Boston, CA, USA, 1991; pp. 141–171. [Google Scholar]
- Page, D.; Wootters, W. Evolution without evolution. Phys. Rev. D 1983, 27, 2885–2892. [Google Scholar] [CrossRef]
- Wootters, W. “Time” replaced by quantum correlations. Int. J. Theor. Phys. 1984, 23, 701–711. [Google Scholar] [CrossRef]
- Rovelli, C. Partial observables. Phys. Rev. D 2002, 65, 124013. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C. The disappearance of space and time. In The Ontology of Spacetime; Dieks, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 25–35. [Google Scholar]
- Rovelli, C. Forget time. Found. Phys. 2011, 41, 1475–1490. [Google Scholar] [CrossRef]
- Horwitz, L.P.; Piron, C. Relativistic dynamics. Helv. Phys. Acta 1973, 46, 316–326. [Google Scholar]
- Horwitz, L.P. An elementary canonical classical and quantum dynamics for general relativity. Eur. Phys. J. Plus 2019, 134, 313. [Google Scholar] [CrossRef]
- Fortin, S.; Lombardi, O.; Pasqualini, M. Relational event-time in quantum mechanics. Found. Phys. 2022, 52, 1–25. [Google Scholar] [CrossRef]
- Schlatter, A. On the foundation of space and time by quantum-events. Found. Phys. 2022, 52, 1–17. [Google Scholar] [CrossRef]
- Cramer, J.G. The transactional interpretation of quantum mechanics. Rev. Mod. Phys. 1986, 58, 647. [Google Scholar] [CrossRef]
- Cramer, J.G. An overview of the transactional interpretation. Int. J. Theor. Phys. 1988, 27, 227–236. [Google Scholar] [CrossRef]
- Kastner, R.E. The Transactional Interpretation of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Kastner, R.E.; Kauffman, S.; Epperson, M. Taking Heisenberg’s potentia seriously. Int. J. Quantum Found. 2018, 4, 158–172. [Google Scholar]
- Lombardi, O.; Castagnino, M. A modal-Hamiltonian interpretation of quantum mechanics. Stud. Hist. Philos. Mod. Phys. 2008, 39, 380–443. [Google Scholar] [CrossRef] [Green Version]
- Lombardi, O.; Castagnino, M.; Ardenghi, J.S. The modal-Hamiltonian interpretation and the Galilean covariance of quantum mechanics. Stud. Hist. Philos. Mod. Phys. 2010, 41, 93–103. [Google Scholar] [CrossRef]
- Ardenghi, J.S.; Lombardi, O.; Narvaja, M. Modal interpretations and consecutive measurements. In EPSA 2011: Perspectives and Foundational Problems in Philosophy of Science; Karakostas, V., Dieks, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 207–217. [Google Scholar]
- Fortin, S.; Lombardi, O.; Martínez González, J.C. A new application of the modal-Hamiltonian interpretation of quantum mechanics: The problem of optical isomerism. Stud. Hist. Philos. Mod. Phys. 2018, 62, 123–135. [Google Scholar] [CrossRef]
- Elitzur, A.; Vaidman, L. Quantum mechanical interaction-free measurements. Found. Phys. 1993, 23, 987–997. [Google Scholar] [CrossRef] [Green Version]
- Kastner, R.E. The Relativistic Transactional Interpretation and spacetime emergence. arXiv 2021, arXiv:2103.11245. [Google Scholar]
- Da Costa, N.; Lombardi, O.; Lastiri, M. A modal ontology of properties for quantum mechanics. Synthese 2013, 190, 3671–3693. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lombardi, O.; Fortin, S.; Pasqualini, M. Possibility and Time in Quantum Mechanics. Entropy 2022, 24, 249. https://doi.org/10.3390/e24020249
Lombardi O, Fortin S, Pasqualini M. Possibility and Time in Quantum Mechanics. Entropy. 2022; 24(2):249. https://doi.org/10.3390/e24020249
Chicago/Turabian StyleLombardi, Olimpia, Sebastian Fortin, and Matías Pasqualini. 2022. "Possibility and Time in Quantum Mechanics" Entropy 24, no. 2: 249. https://doi.org/10.3390/e24020249
APA StyleLombardi, O., Fortin, S., & Pasqualini, M. (2022). Possibility and Time in Quantum Mechanics. Entropy, 24(2), 249. https://doi.org/10.3390/e24020249






