Stochastic Theory of Discrete Binary Fragmentation—Kinetics and Thermodynamics
Abstract
:1. Introduction
2. Statistical Thermodynamics of the Cluster Ensemble
3. Binary Fragmentation
3.1. Fragmentation Kernel
3.2. Fragmentation Ensemble
3.3. Transitions between Distributions
3.4. Kinetics and Thermodynamics
3.5. Mean Distribution
4. Special Case: Random Fragmentation
5. Shattering
5.1. Power-Law Breakage
5.2. Stability and Phase Transitions
5.3. Monte Carlo Simulations of Shattering
6. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stockmayer, W.H. Theory of Molecular Size Distribution and Gel Formation in Branched-Chain Polymers. J. Chem. Phys. 1943, 11, 45–55. [Google Scholar] [CrossRef]
- Ziff, R.M.; Stell, G. Kinetics of polymer gelation. J. Chem. Phys. 1980, 73, 3492–3499. [Google Scholar] [CrossRef]
- Lushnikov, A.A. From Sol to Gel Exactly. Phys. Rev. Lett. 2004, 93, 198302. [Google Scholar] [CrossRef] [PubMed]
- Matsoukas, T. Statistical Thermodynamics of Irreversible Aggregation: The Sol-Gel Transition. Sci. Rep. 2015, 5, 8855. [Google Scholar] [CrossRef] [PubMed]
- Filippov, A.F. On the Distribution of the Sizes of Particles which Undergo Splitting. J. Theory Prob. Appl. 1961, 6, 275–294. [Google Scholar] [CrossRef]
- McGrady, E.D.; Ziff, R.M. “Shattering” Transition in Fragmentation. Phys. Rev. Lett. 1987, 58, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Redner, S. Kinetics of fragmentation. J. Phys. A Math. Gen. 1990, 23, 1233. [Google Scholar] [CrossRef] [Green Version]
- Ernst, M.H.; Szamel, G. Fragmentation kinetics. J. Phys. A Math. Gen. 1993, 26, 6085. [Google Scholar] [CrossRef]
- Boyer, D.; Tarjus, G.; Viot, P. Shattering transition in a multivariable fragmentation model. Phys. Rev. E 1995, 51, 1043–1046. [Google Scholar] [CrossRef]
- Singh, P.; Hassan, M.K. Kinetics of multidimensional fragmentation. Phys. Rev. E 1996, 53, 3134–3144. [Google Scholar] [CrossRef] [Green Version]
- Krapivsky, P.L.; Ben-Naim, E. Shattering transitions in collision-induced fragmentation. Phys. Rev. E 2003, 68, 021102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banasiak, J. Conservative And Shattering Solutions for some classes of fragmentation models. Math. Models Methods Appl. Sci. 2004, 14, 483–501. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Otieno, W.; Brilliantov, N.V. Phase transitions in systems with aggregation and shattering. Phys. Rev. E 2017, 96, 042138. [Google Scholar] [CrossRef] [Green Version]
- Matveev, S.A.; Krapivsky, P.L.; Smirnov, A.P.; Tyrtyshnikov, E.E.; Brilliantov, N.V. Oscillations in Aggregation-Shattering Processes. Phys. Rev. Lett. 2017, 119, 260601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Connaughton, C.; Dutta, A.; Rajesh, R.; Siddharth, N.; Zaboronski, O. Stationary mass distribution and nonlocality in models of coalescence and shattering. Phys. Rev. E 2018, 97, 022137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziff, R.M.; McGrady, E.D. Kinetics of polymer degradation. Macromolecules 1986, 19, 2513–2519. [Google Scholar] [CrossRef]
- Matsoukas, T. Statistical thermodynamics of clustered populations. Phys. Rev. E 2014, 90, 022113. [Google Scholar] [CrossRef] [Green Version]
- Matsoukas, T. Thermodynamics Beyond Molecules: Statistical Thermodynamics of Probability Distributions. Entropy 2019, 21, 890. [Google Scholar] [CrossRef] [Green Version]
- Matsoukas, T. The Smoluchowski Ensemble—Statistical Mechanics of Aggregation. Entropy 2020, 22, 1181. [Google Scholar] [CrossRef]
- Matsoukas, T. Generalized Statistical Thermodynamics: Thermodynamics of Probability Distributions and Stochastic Processes; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Matsoukas, T. Statistical Mechanics of Discrete Multicomponent Fragmentation. Condens. Matter 2020, 5, 64. [Google Scholar] [CrossRef]
- Durrett, R.; Granovsky, B.; Gueron, S. The Equilibrium Behavior of Reversible Coagulation-Fragmentation Processes. J. Theor. Probab. 1999, 12, 447–474. [Google Scholar] [CrossRef]
- Evans, M.R.; Hanney, T. Nonequilibrium statistical mechanics of the zero-range process and related models. J. Phys. A Math. Gen. 2005, 38, R195–R240. [Google Scholar] [CrossRef] [Green Version]
- Berestycki, N.; Pitman, J. Gibbs Distributions for Random Partitions Generated by a Fragmentation Process. J. Stat. Phys. 2007, 127, 381–418. [Google Scholar] [CrossRef] [Green Version]
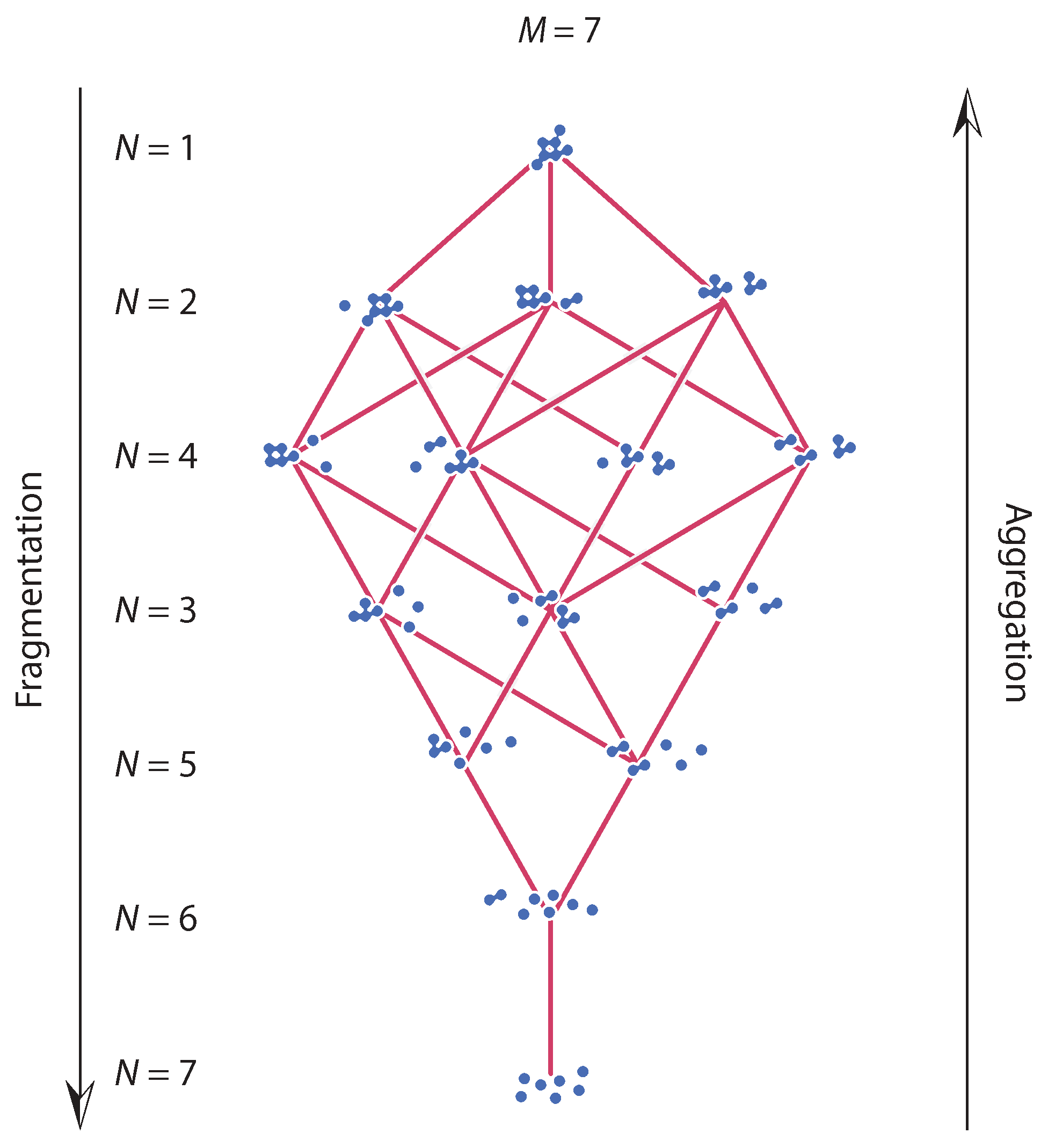
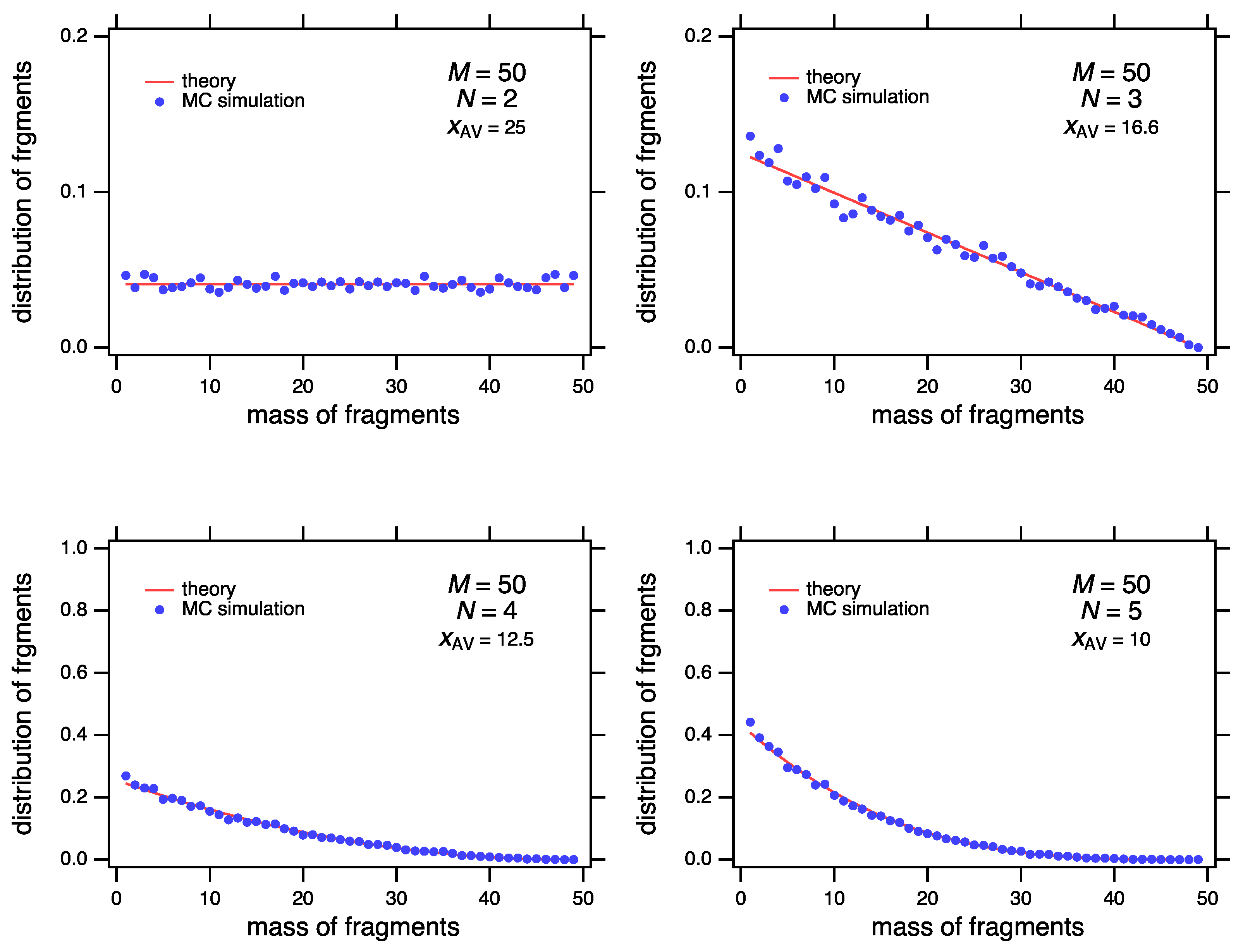
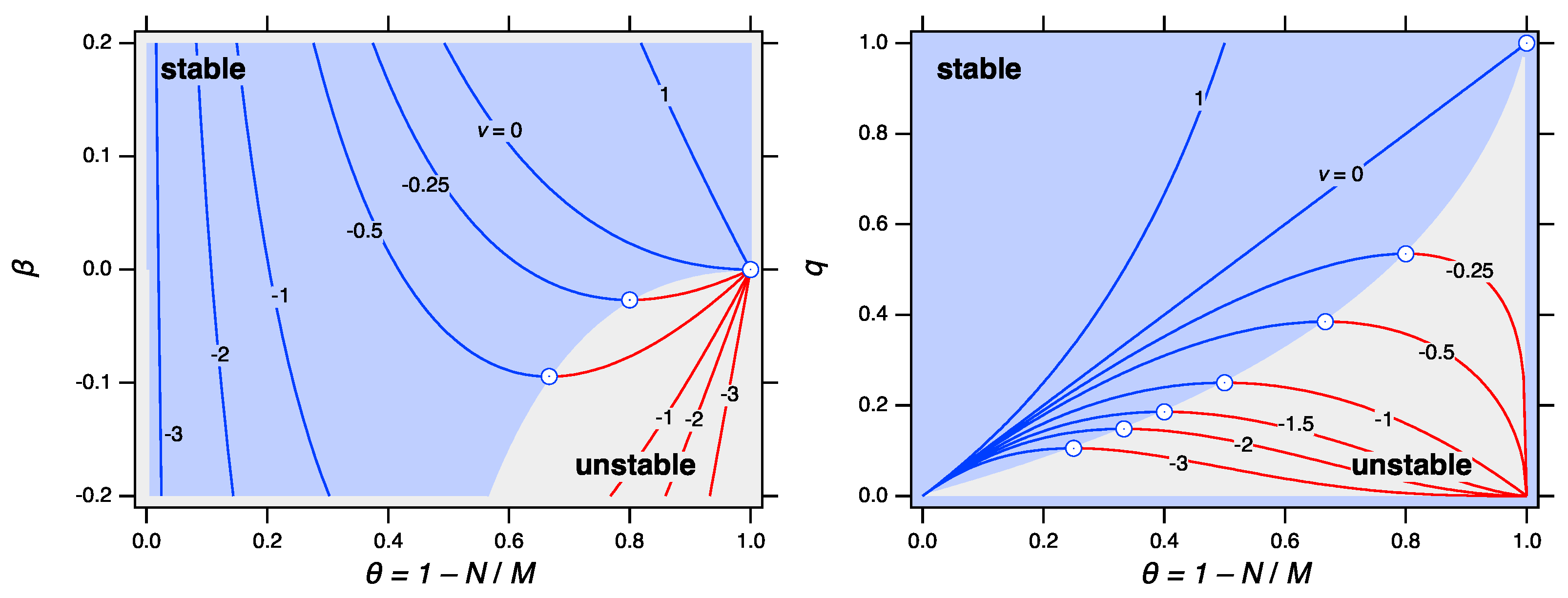
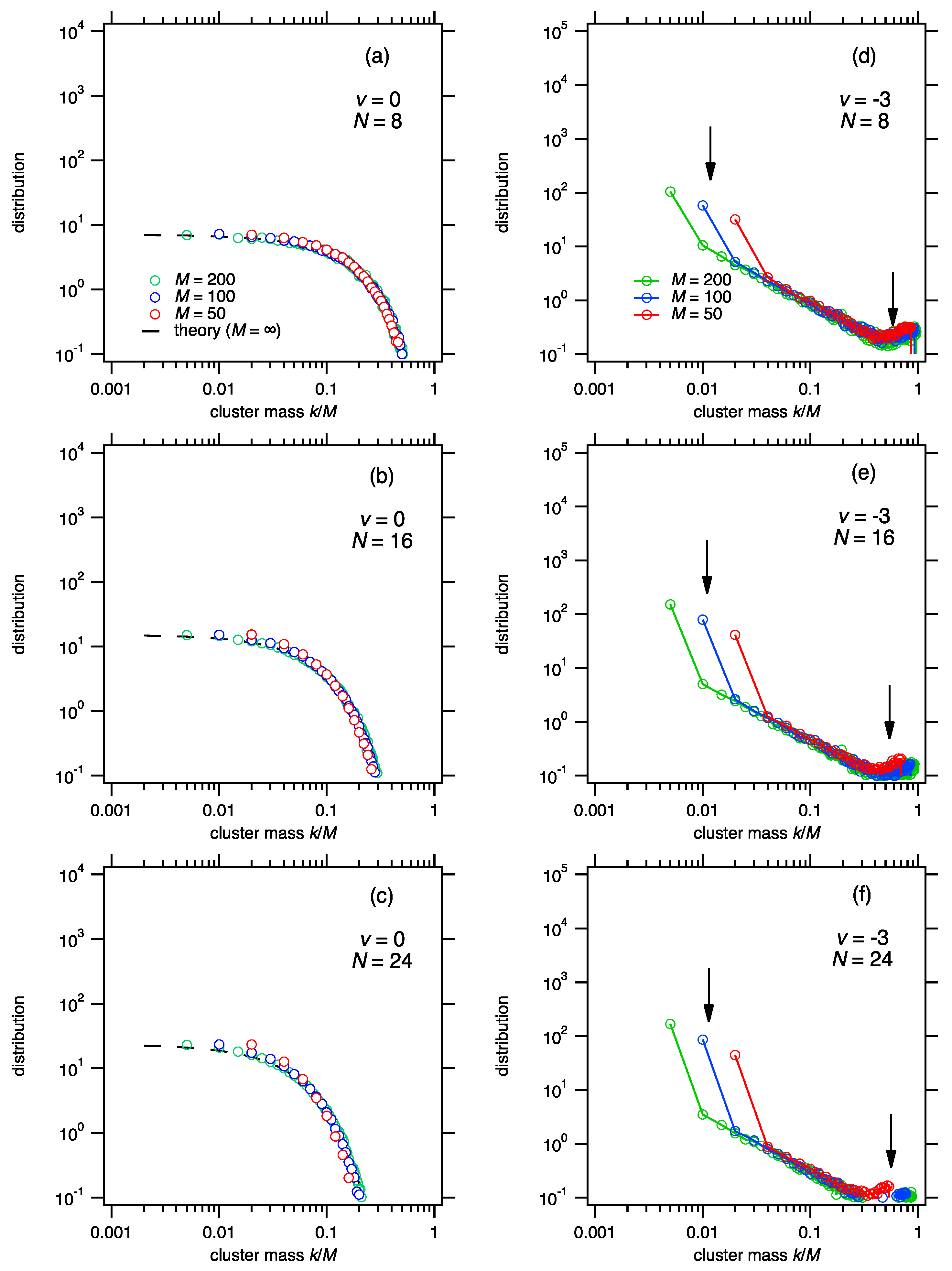
| Number of Fragments, N | Distribution of Fragments |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 |
| Fragmentation | Aggregation | |
|---|---|---|
| kernel | ||
| − | − | |
| q | ||
| stability |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsoukas, T. Stochastic Theory of Discrete Binary Fragmentation—Kinetics and Thermodynamics. Entropy 2022, 24, 229. https://doi.org/10.3390/e24020229
Matsoukas T. Stochastic Theory of Discrete Binary Fragmentation—Kinetics and Thermodynamics. Entropy. 2022; 24(2):229. https://doi.org/10.3390/e24020229
Chicago/Turabian StyleMatsoukas, Themis. 2022. "Stochastic Theory of Discrete Binary Fragmentation—Kinetics and Thermodynamics" Entropy 24, no. 2: 229. https://doi.org/10.3390/e24020229
APA StyleMatsoukas, T. (2022). Stochastic Theory of Discrete Binary Fragmentation—Kinetics and Thermodynamics. Entropy, 24(2), 229. https://doi.org/10.3390/e24020229






