A Bounded Measure for Estimating the Benefit of Visualization (Part I): Theoretical Discourse and Conceptual Evaluation
Abstract
:1. Introduction
- Identifying a shortcoming of using the KL-divergence in the information-theoretic measure proposed by Chen and Golan [1] and evidencing the shortcoming using practical examples (Parts I and II);
- Presenting a theoretical discourse to justify the use of a bounded measure for finite alphabets (Part I);
- Proposing a new bounded divergence measure, while studying existing bounded divergence measures (Part I);
- Analyzing nine candidate measures using seven criteria reflecting desirable conceptual or mathematical properties, and narrowing the nine candidate measures to six measures (Part I);
- Conducting several case studies for collecting instances for evaluating the remaining six candidate measures (Part II);
- Demonstrating the uses of the cost–benefit measurement to estimate the benefit of visualization in practical scenarios and the human knowledge used in the visualization processes (Part II);
- Discovering a new conceptual criterion that a divergence measure is a summation of the entropic values of its components, which is useful in analyzing and visualizing empirical data (Part II);
- Offering a recommendation to revise the information-theoretic measure proposed by Chen and Golan [1] based on multi-criteria decision analysis (Parts I and II).
2. Related Work
3. Overview and Motivation
4. Mathematical Notations and Problem Statement
4.1. Mathematical Notation
4.2. Problem Statement
5. Bounded Measures for Potential Distortion (PD)
5.1. A Conceptual Proof of Boundedness
5.2. Existing Candidates of Bounded Measures
5.3. New Candidates of Bounded Measures
6. Conceptual Evaluation of Bounded Measures
6.1. Criterion 1: Is It a Bounded Measure?
6.2. Criterion 2: How Many PMFs Does It Have as Dependent Variables
6.3. Criterion 3: Is It an Entropic Measure?
6.4. Criterion 4: Is It a Distance Measure?
- identity: ,
- symmetry: ,
- triangle inequality: ,
- non-negativity: .
6.5. Criterion 5: Is It Intuitive or Easy to Understand?
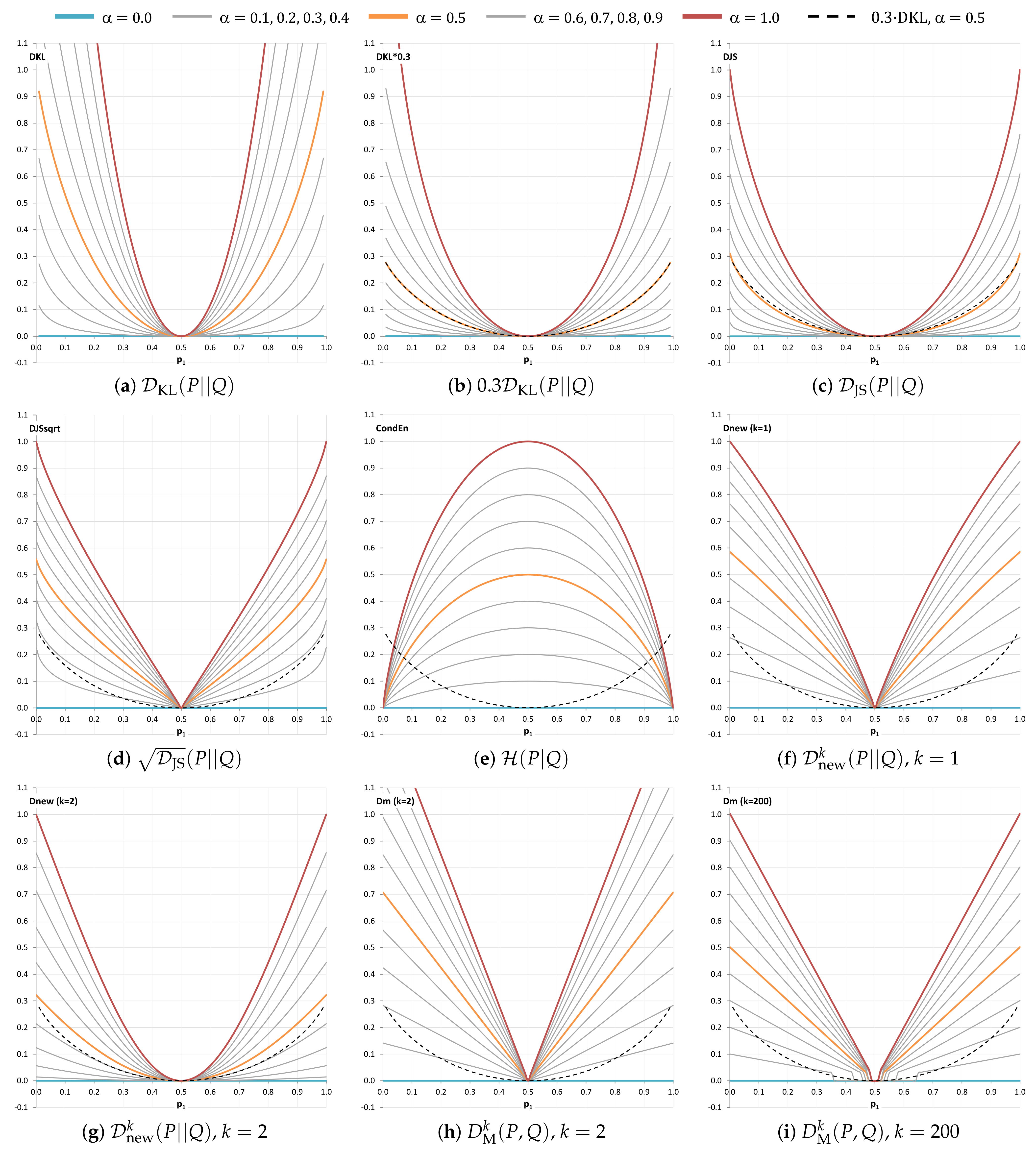
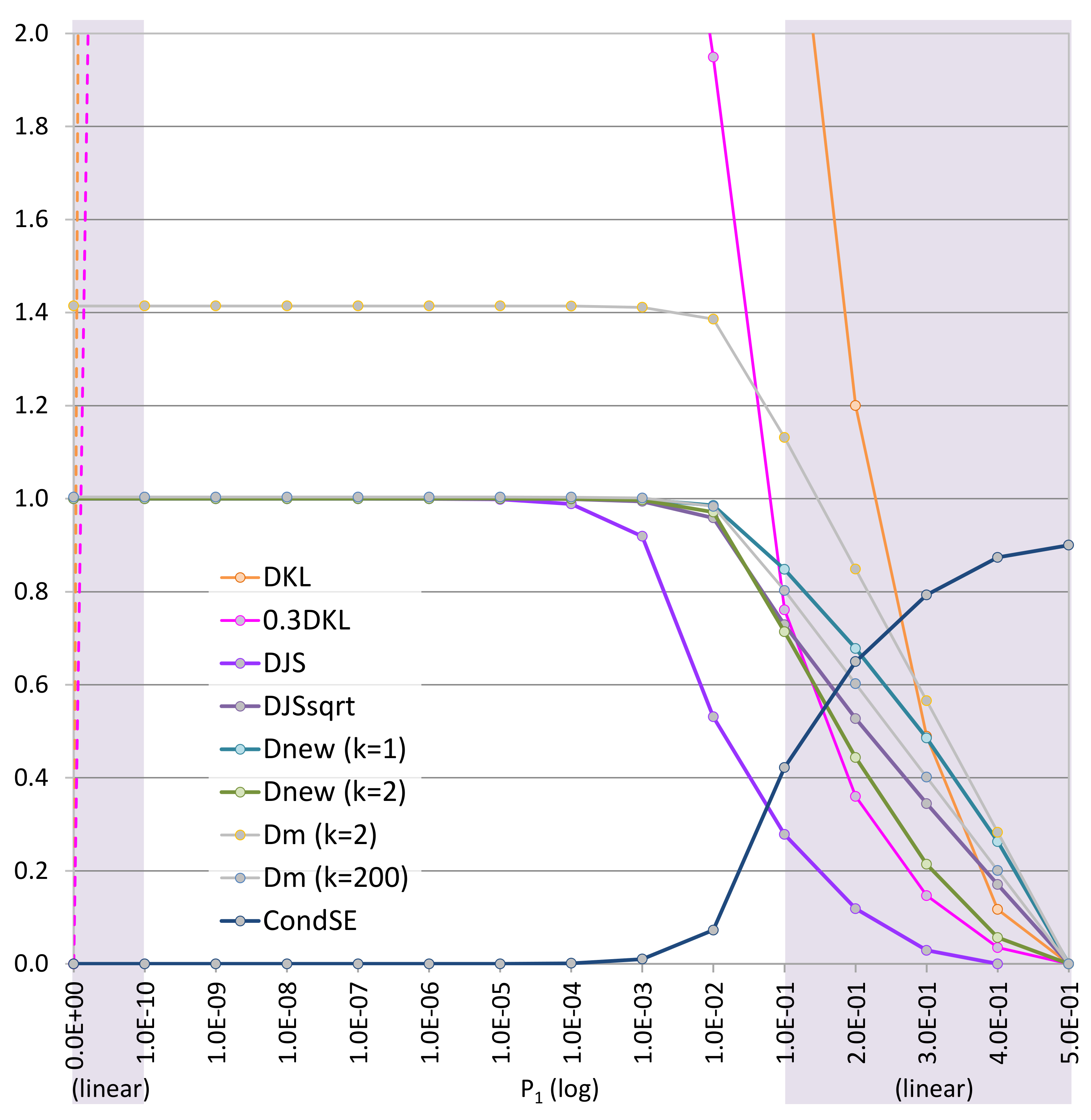
6.6. Criterion 6: Visual Analysis of Curve Shapes in the Range of
6.7. Criterion 7: Visual Analysis of Curve Shapes in a Range near Zero, i.e.,
7. Discussions and Conclusions
- It is not intuitive to interpret a set of values that would indicate that the amount of distortion in viewing a visualization that features some information loss, could be much more than the total amount of information contained in the visualization.
- It is difficult to specify some simple visualization phenomena. For example, before a viewer observes a variable x using visualization, the viewer incorrectly assumes that the variable is a constant (e.g., , and probability ). The KL-divergence cannot measure the potential distortion of this phenomenon of bias because this is a singularity condition, unless one changes by subtracting a small value .
- If one tries to restrict the KL-divergence to return values within a bounded range, e.g., determined by the maximum entropy of the visualization space or the underlying data space, one could potentially lose a non-trivial portion of the probability range (e.g., in the case of a binary alphabet).
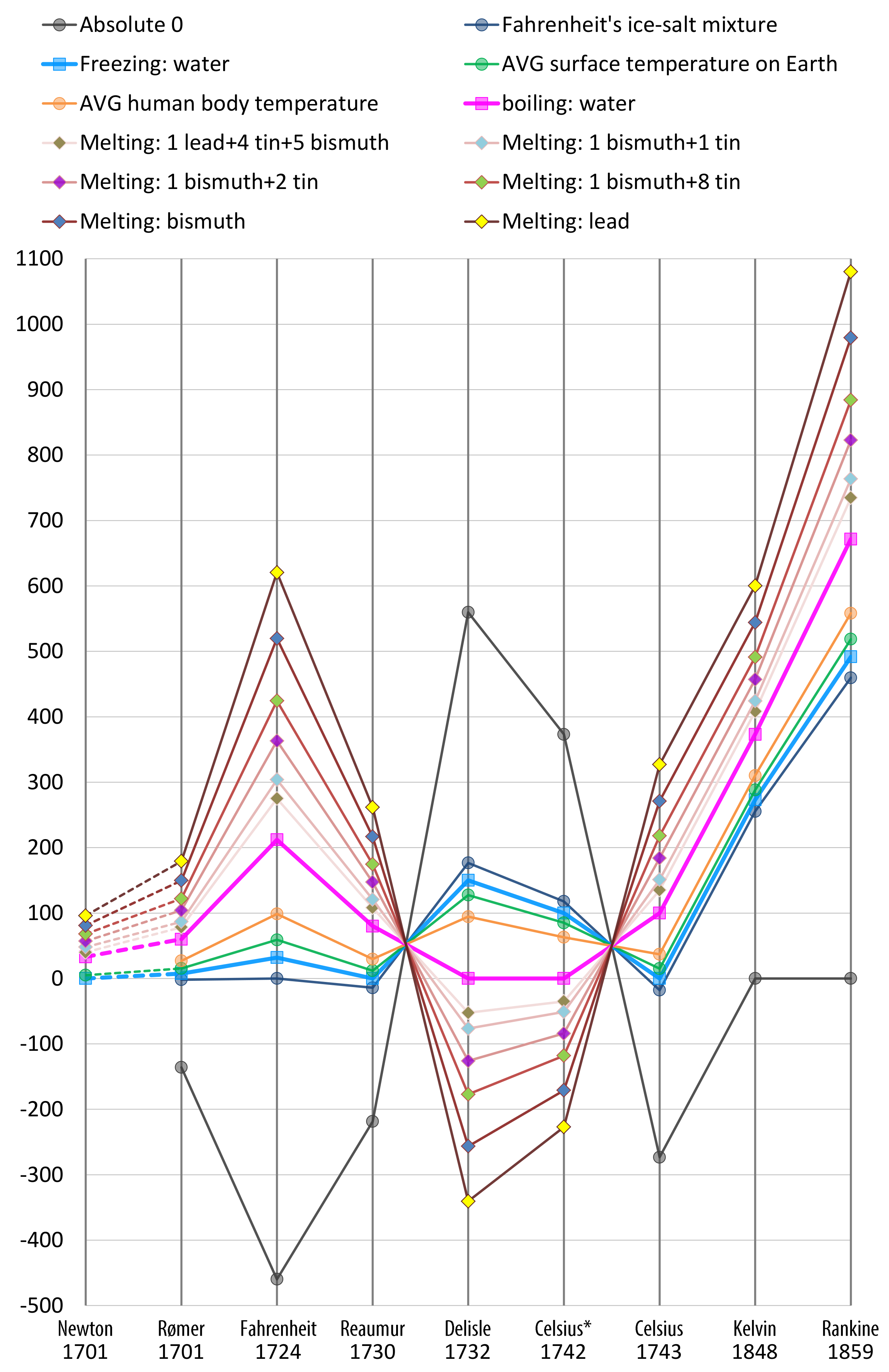
- Rømer—0 degree: freezing brine, 7.5 degree: the freezing point of water, 60 degree: the boiling point of water;
- Fahrenheit (original)—0 degree: the freezing point of brine (a high-concentration solution of salt in water), 32 degree: ice water, 96 degree: average human body temperature;
- Fahrenheit (present)—32 degree: the freezing point of water, 212 degree: the boiling point of water;
- Réaumur—0 degree: the freezing point of water, 80 degree: the boiling point of water;
- Delisle—0 degree: the boiling point of water, degree; the contraction of the mercury in hundred-thousandths.
- Celsius* (original)—0 degree: the boiling point of water, 100 degree: the freezing point of water;
- Celsius (1743–1954)—0 degree: the freezing point of water, 100 degree: the boiling point of water;
- Celsius (1954–2019)—redefined based on absolute zero and the triple point of VSMOW (specially prepared water);
- Celsius (2019–now)—redefined based on the Boltzmann constant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alphabet Compression |
| JS | Jenson–Shannon |
| KL | Kullback–Leibler |
| MCDA | Multi-Criteria Decision Analysis |
| MIP | Maximum Intensity Projection |
| PD | Potential Distortion |
| PMF | Probability Mass Function |
Appendix A. Conceptual Boundedness of 𝓗CE(P,Q) and 𝓓KL
- if , codeword 0 for and codeword 1 for ;
- if , codeword 0 for and codeword 10 for ;
- ⋯
- if , codeword 0 for and codeword 111111 for ;
- ⋯

References
- Chen, M.; Golan, A. What May Visualization Processes Optimize? IEEE Trans. Vis. Comput. Graph. 2016, 22, 2619–2632. [Google Scholar] [CrossRef] [Green Version]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis: Methods and Software; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Abdul-Rahman, A.; Silver, D.; Sbert, M. A Bounded Measure for Estimating the Benefit of Visualization (Part II): Case Studies and Empirical Evaluation. (earlier version: arXiv:2103.02502). arXiv, 2022; under review. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chen, M.; Feixas, M.; Viola, I.; Bardera, A.; Shen, H.W.; Sbert, M. Information Theory Tools for Visualization; A K Peters: Natick, MA, USA, 2016. [Google Scholar]
- Feixas, M.; del Acebo, E.; Bekaert, P.; Sbert, M. An Information Theory Framework for the Analysis of Scene Complexity. Comput. Graph. Forum 1999, 18, 95–106. [Google Scholar] [CrossRef]
- Rigau, J.; Feixas, M.; Sbert, M. Shape Complexity Based on Mutual Information. In Proceedings of the IEEE Shape Modeling and Applications, Cambridge, MA, USA, 13–17 June 2005. [Google Scholar]
- Gumhold, S. Maximum entropy light source placement. In Proceedings of the IEEE Visualization, Boston, MA, USA, 27 October–1 November 2002; pp. 275–282. [Google Scholar]
- Vázquez, P.P.; Feixas, M.; Sbert, M.; Heidrich, W. Automatic View Selection Using Viewpoint Entropy and its Application to Image-Based Modelling. Comput. Graph. Forum 2004, 22, 689–700. [Google Scholar] [CrossRef]
- Feixas, M.; Sbert, M.; González, F. A unified information-theoretic framework for viewpoint selection and mesh saliency. ACM Trans. Appl. Percept. 2009, 6, 1–23. [Google Scholar] [CrossRef]
- Ng, C.U.; Martin, G. Automatic selection of attributes by importance in relevance feedback visualisation. In Proceedings of the Information Visualisation, London, UK, 14–16 July 2004; pp. 588–595. [Google Scholar]
- Bordoloi, U.; Shen, H.W. View selection for volume rendering. In Proceedings of the IEEE Visualization, Minneapolis, MN, USA, 23–28 October 2005; pp. 487–494. [Google Scholar]
- Takahashi, S.; Takeshima, Y. A Feature-Driven Approach to Locating Optimal Viewpoints for Volume Visualization. In Proceedings of the IEEE Visualization, Minneapolis, MN, USA, 23–28 October 2005; pp. 495–502. [Google Scholar]
- Wang, C.; Shen, H.W. LOD Map—A Visual Interface for Navigating Multiresolution Volume Visualization. IEEE Trans. Vis. Comput. Graph. 2005, 12, 1029–1036. [Google Scholar] [CrossRef] [Green Version]
- Viola, I.; Feixas, M.; Sbert, M.; Gröller, M.E. Importance-Driven Focus of Attention. IEEE Trans. Vis. Comput. Graph. 2006, 12, 933–940. [Google Scholar] [CrossRef] [Green Version]
- Jänicke, H.; Wiebel, A.; Scheuermann, G.; Kollmann, W. Multifield Visualization Using Local Statistical Complexity. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1384–1391. [Google Scholar]
- Jänicke, H.; Scheuermann, G. Visual Analysis of Flow Features Using Information Theory. IEEE Comput. Graph. Appl. 2010, 30, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yu, H.; Ma, K.L. Importance-Driven Time-Varying Data Visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1547–1554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bruckner, S.; Möller, T. Isosurface similarity maps. Comput. Graph. Forum 2010, 29, 773–782. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, M.; Bardera, A.; Boada, I.; Viola, I.; Feixas, M.; Sbert, M. Automatic transfer functions based on informational divergence. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1932–1941. [Google Scholar] [CrossRef] [Green Version]
- Bramon, R.; Ruiz, M.; Bardera, A.; Boada, I.; Feixas, M.; Sbert, M. Information Theory-Based Automatic Multimodal Transfer Function Design. IEEE J. Biomed. Health Inform. 2013, 17, 870–880. [Google Scholar] [CrossRef]
- Bramon, R.; Boada, I.; Bardera, A.; Rodríguez, Q.; Feixas, M.; Puig, J.; Sbert, M. Multimodal Data Fusion based on Mutual Information. IEEE Trans. Vis. Comput. Graph. 2012, 18, 1574–1587. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.H.; Lee, T.Y.; Shen, H.W. Evaluating Isosurfaces with Level-set-based Information Maps. Comput. Graph. Forum 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Bramon, R.; Ruiz, M.; Bardera, A.; Boada, I.; Feixas, M.; Sbert, M. An Information-Theoretic Observation Channel for Volume Visualization. Comput. Graph. Forum 2013, 32, 411–420. [Google Scholar] [CrossRef]
- Biswas, A.; Dutta, S.; Shen, H.W.; Woodring, J. An Information-Aware Framework for Exploring Multivariate Data Sets. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2683–2692. [Google Scholar] [CrossRef]
- Chen, M.; Jänicke, H. An Information-theoretic Framework for Visualization. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1206–1215. [Google Scholar] [CrossRef]
- Chen, M.; Walton, S.; Berger, K.; Thiyagalingam, J.; Duffy, B.; Fang, H.; Holloway, C.; Trefethen, A.E. Visual multiplexing. Comput. Graph. Forum 2014, 33, 241–250. [Google Scholar] [CrossRef]
- Purchase, H.C.; Andrienko, N.; Jankun-Kelly, T.J.; Ward, M. Theoretical Foundations of Information Visualization. In Information Visualization: Human-Centered Issues and Perspectives; LNCS 4950; Springer: Berlin, Germany, 2008; pp. 46–64. [Google Scholar]
- Xu, L.; Lee, T.Y.; Shen, H.W. An information-theoretic framework for flow visualization. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1216–1224. [Google Scholar] [PubMed]
- Wang, C.; Shen, H.W. Information Theory in Scientific Visualization. Entropy 2011, 13, 254–273. [Google Scholar] [CrossRef] [Green Version]
- Tam, G.K.L.; Kothari, V.; Chen, M. An analysis of machine- and human-analytics in classification. IEEE Trans. Vis. Comput. Graph. 2017, 23, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Kijmongkolchai, N.; Abdul-Rahman, A.; Chen, M. Empirically measuring soft knowledge in visualization. Comput. Graph. Forum 2017, 36, 73–85. [Google Scholar] [CrossRef]
- Chen, M.; Gaither, K.; John, N.W.; McCann, B. cost–benefit analysis of visualization in virtual environments. IEEE Trans. Vis. Comput. Graph. 2019, 25, 32–42. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Ebert, D.S. An ontological framework for supporting the design and evaluation of visual analytics systems. Comput. Graph. Forum 2019, 38, 131–144. [Google Scholar] [CrossRef]
- Streeb, D.; El-Assady, M.; Keim, D.; Chen, M. Why visualize? Untangling a large network of arguments. IEEE Trans. Vis. Comput. Graph. 2019, 27, 2220–2236. [Google Scholar] [CrossRef]
- Viola, I.; Chen, M.; Isenberg, T. Visual Abstraction. In Foundations of Data Visualization; Springer: Berlin, Germany, 2020. [Google Scholar]
- Tennekes, M.; Chen, M. Design Space of Origin-Destination Data Visualization. Computer Graphics Forum 2021, 40, 323–334. [Google Scholar] [CrossRef]
- Chen, M.; Grinstein, G.; Johnson, C.R.; Kennedy, J.; Tory, M. Pathways for Theoretical Advances in Visualization. IEEE Comput. Graph. Appl. 2017, 37, 103–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M. Cost–benefit Analysis of Data Intelligence—Its Broader Interpretations. In Advances in Info-Metrics: Information and Information Processing across Disciplines; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Chen, M. A Short Introduction to Information-Theoretic cost–benefit Analysis. arXiv 2021, arXiv:2103.15113. [Google Scholar]
- Chen, M.; Sbert, M. On the Upper Bound of the Kullback–Leibler Divergence and Cross Entropy. arXiv 2019, arXiv:1911.08334. [Google Scholar]
- Moser, S.M. A Student’s Guide to Coding and Information Theory; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef] [Green Version]
- Ôsterreicher, F.; Vajda, I. A new class of metric divergences on probability spaces and its statistical applications. Ann. Inst. Stat. Math. 2003, 55, 639–653. [Google Scholar] [CrossRef]
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inf. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremos, P. Rényi Divergence and Kullback–Leibler Divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef] [Green Version]
- Klein, H.A. The Science of Measurement: A Historical Survey; Dover Publications: Mineola, NY, USA, 2012. [Google Scholar]
- Pedhazur, E.J.; Schmelkin, L.P. Measurement, Design, and Analysis: An Integrated Approach; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1991. [Google Scholar]
- Haseli, G.; Sheikh, R.; Sana, S.S. Base-criterion on multi-criteria decision-making method and its applications. Int. J. Manag. Sci. Eng. Manag. 2020, 15, 79–88. [Google Scholar] [CrossRef]
- Chen, M.; Sbert, M. Is the Chen-Sbert Divergence a Metric? arXiv 2021, arXiv:2101.06103. [Google Scholar]
- Newton, I. Scala graduum caloris. Philos. Trans. 1701, 22, 824–829. [Google Scholar]
- Golin, M.J. Lecture 17: Huffman Coding. Available online: http://home.cse.ust.hk/faculty/golin/COMP271Sp03/Notes/MyL17.pdf (accessed on 15 March 2020).
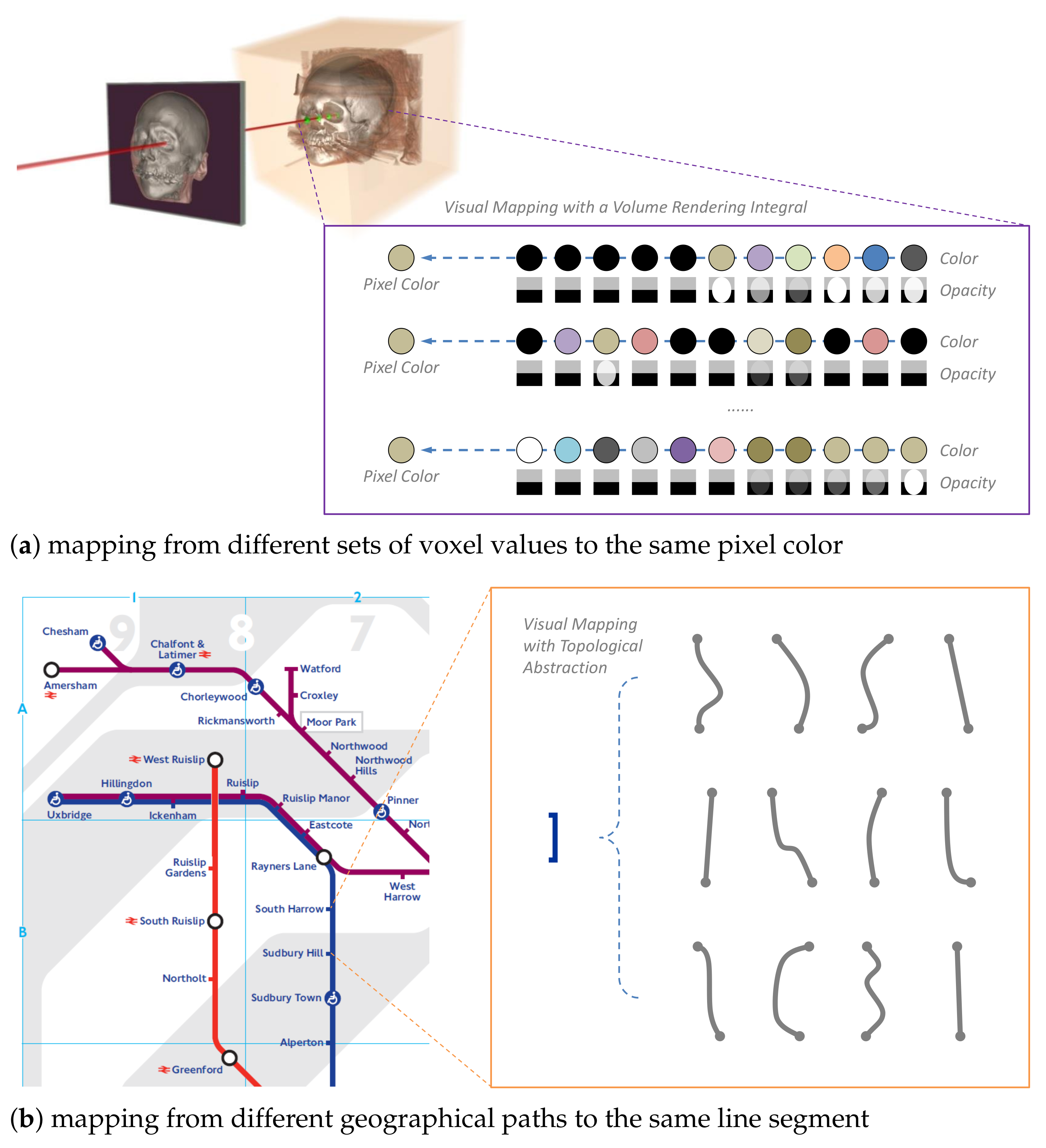

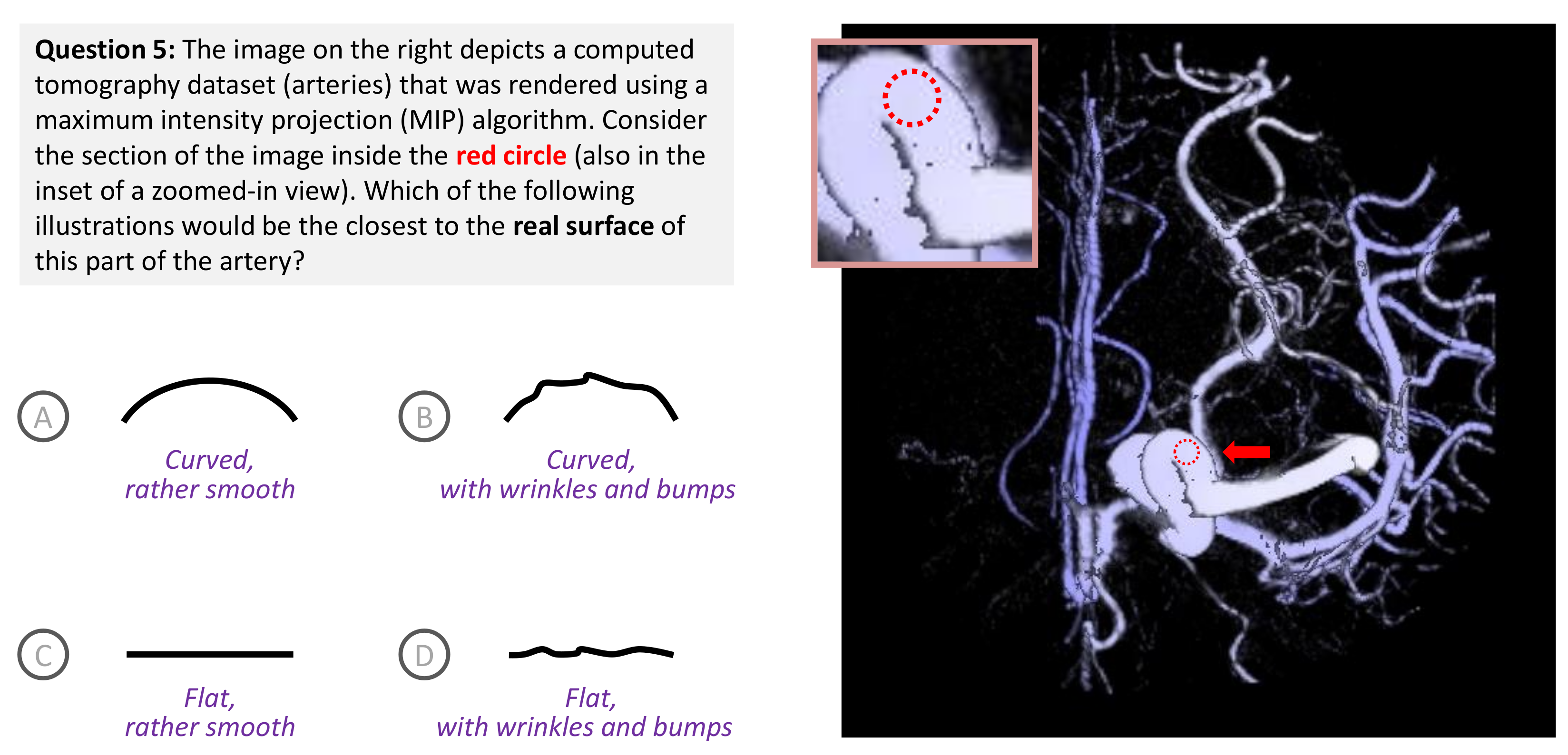
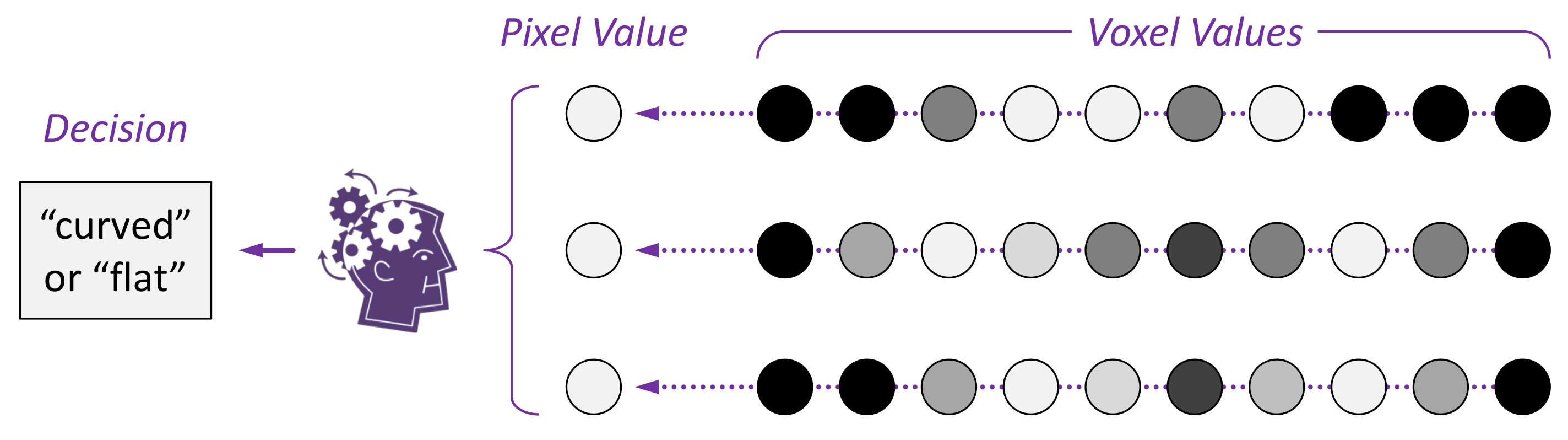
| Scenario 1 | Scenario 2 | |
|---|---|---|
| : | ||
| : | ||
| : | ||
| : |
| Scenario 3 | Scenario 4 | |
|---|---|---|
| : | ||
| : | ||
| : | ||
| : |
| Criteria | Importance | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Boundedness | critical | 0 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 3 | 3 |
| ▸ is eliminated but used below only for comparison. The other scores are carried forward. | |||||||||||
| 2. Number of PMFs | important | 5 | 5 | 5 | 2 | 5 | 5 | 5 | 5 | 5 | 5 |
| 3. Entropic measures | important | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 1 | 1 |
| 4. Distance metric | helpful | 2 | 3 | 5 | 2 | 4 | 3 | 2 | 2 | 5 | 5 |
| 5. Easy to understand | helpful | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 3 | 5 | 4 |
| 6. Curve shapes (Figure 5) | helpful | 5 | 5 | 3 | 1 | 2 | 4 | 2 | 4 | 2 | 2 |
| 7. Curve shapes (Figure 6) | helpful | 5 | 3 | 4 | 1 | 3 | 5 | 3 | 5 | 2 | 3 |
| ▸Eliminate, , based on criteria 1–7 | sum: | 30 | 30 | 20 | 28 | 30 | 26 | 29 | 23 | 23 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Sbert, M. A Bounded Measure for Estimating the Benefit of Visualization (Part I): Theoretical Discourse and Conceptual Evaluation. Entropy 2022, 24, 228. https://doi.org/10.3390/e24020228
Chen M, Sbert M. A Bounded Measure for Estimating the Benefit of Visualization (Part I): Theoretical Discourse and Conceptual Evaluation. Entropy. 2022; 24(2):228. https://doi.org/10.3390/e24020228
Chicago/Turabian StyleChen, Min, and Mateu Sbert. 2022. "A Bounded Measure for Estimating the Benefit of Visualization (Part I): Theoretical Discourse and Conceptual Evaluation" Entropy 24, no. 2: 228. https://doi.org/10.3390/e24020228
APA StyleChen, M., & Sbert, M. (2022). A Bounded Measure for Estimating the Benefit of Visualization (Part I): Theoretical Discourse and Conceptual Evaluation. Entropy, 24(2), 228. https://doi.org/10.3390/e24020228






