Effects of Vaccination Efficacy on Wealth Distribution in Kinetic Epidemic Models
Abstract
:1. Introduction
2. Wealth Dynamics in Epidemic Phenomena
2.1. The Kinetic Model
2.2. Evolution of Macroscopic Quantities
3. Properties of the Kinetic Model
3.1. Fokker–Planck Scaling and Steady States
4. Numerical Results
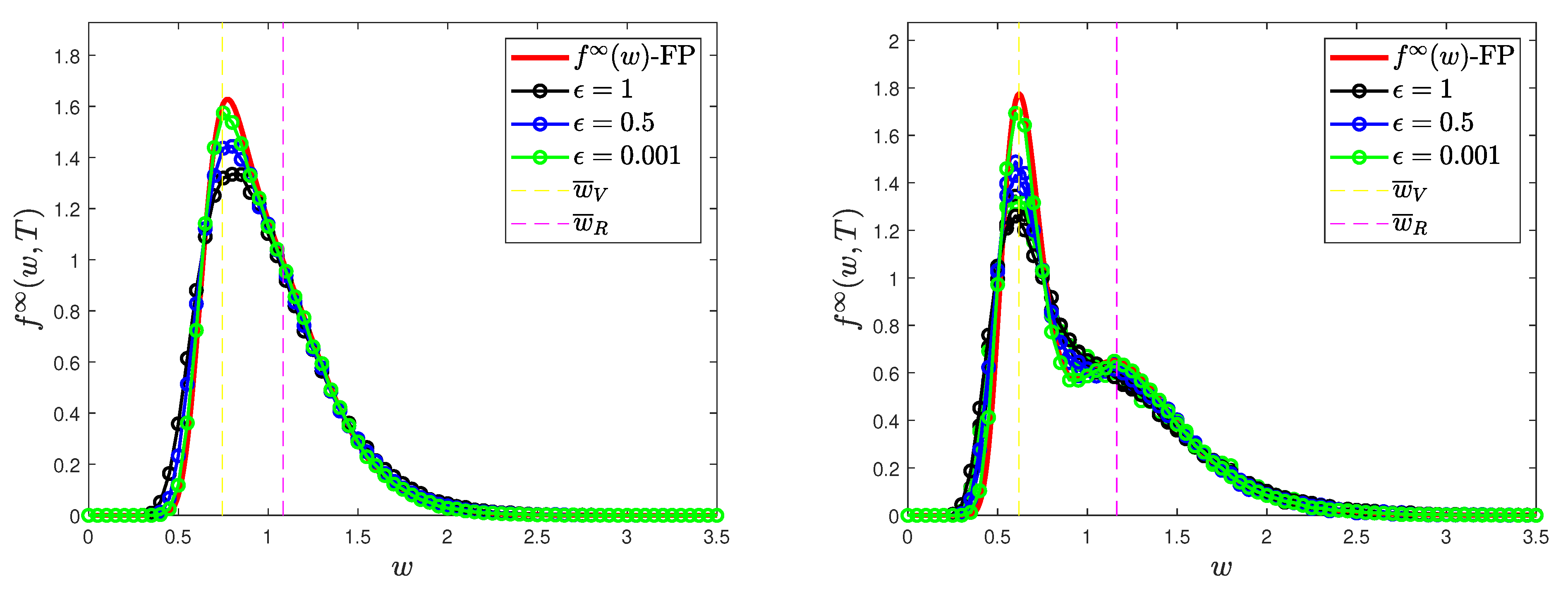
4.1. Test 1: Long-Time Behavior and Convergence to Equilibrium
- , , ,
- , , ,
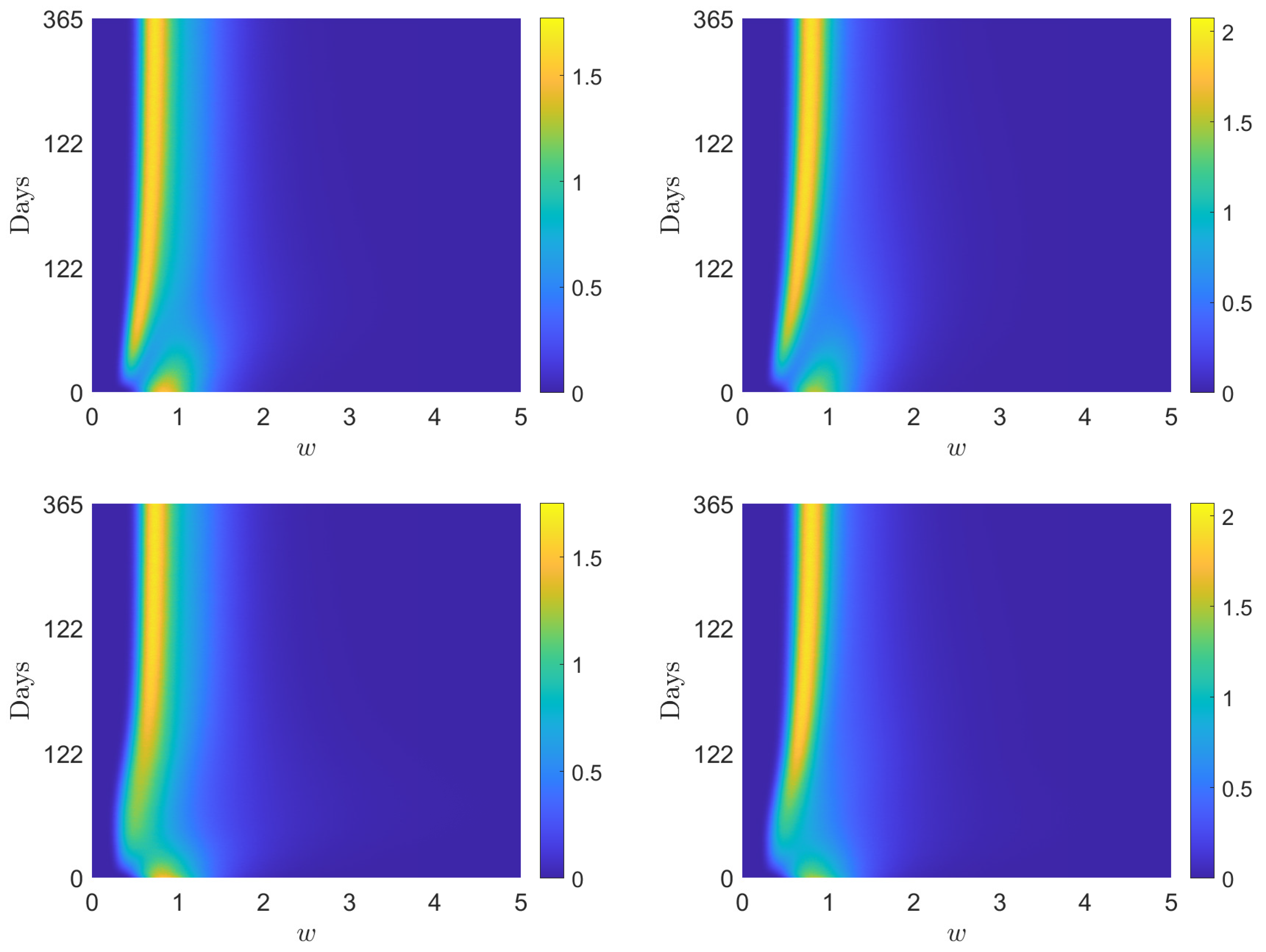
4.2. Test 2: Wealth Inequalities and Vaccination Campaign
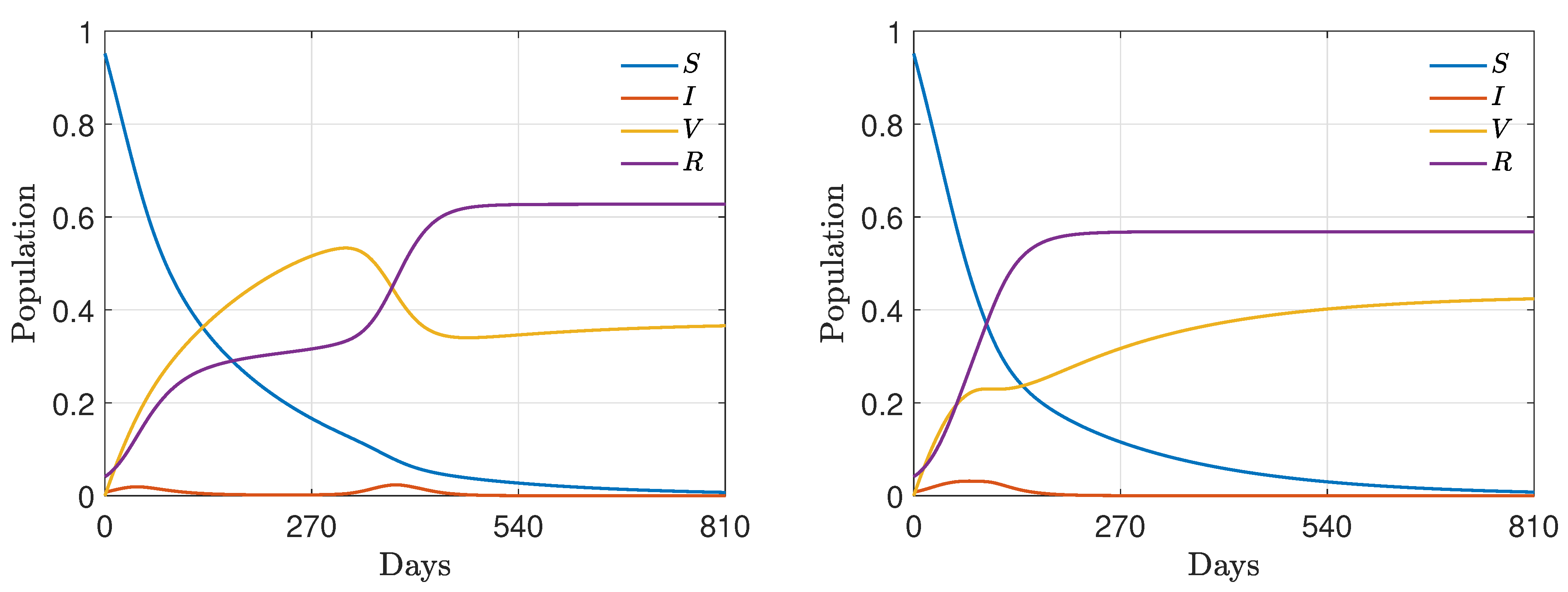
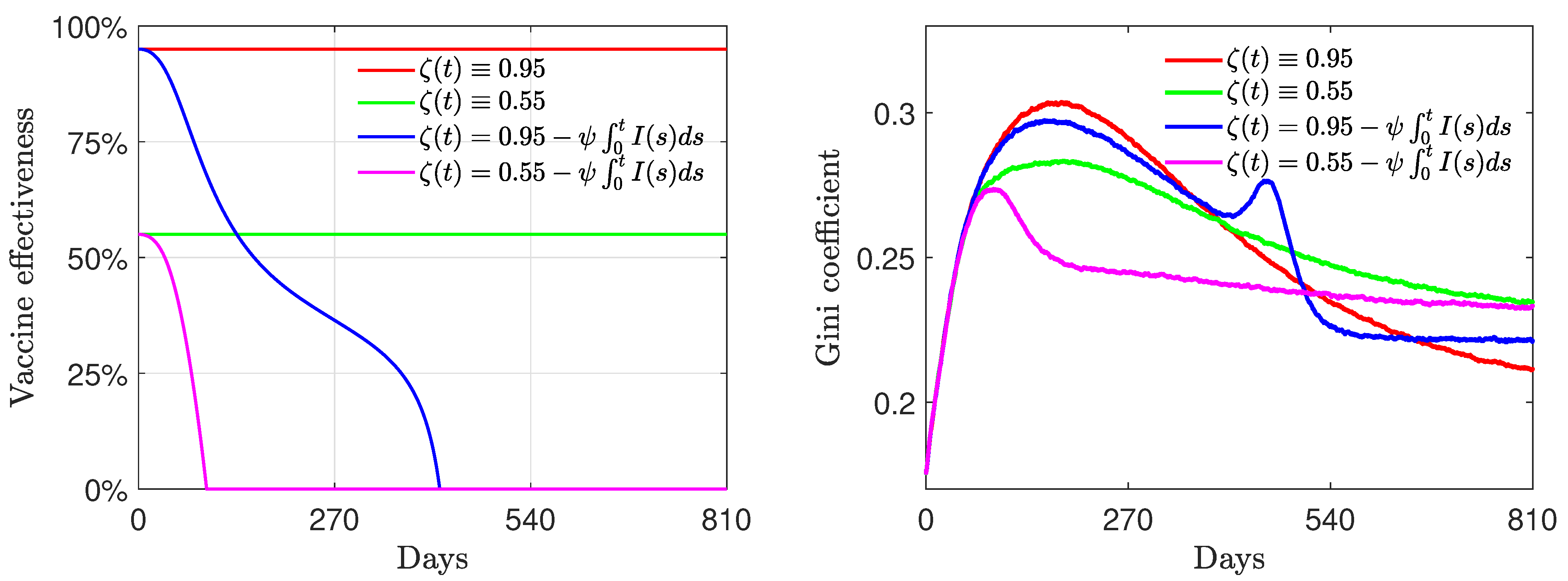
4.3. Nonlinear Incidence Rate and Time-Varying Vaccine Efficacy
4.3.1. Test 3A:
4.3.2. Test 3B:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dimarco, G.; Pareschi, L.; Toscani, G.; Zanella, M. Wealth distribution under the spread of infectious diseases. Phys. Rev. E 2020, 102, 022303. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Text in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 69. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599. [Google Scholar] [CrossRef] [Green Version]
- Cordier, S.; Pareschi, L.; Toscani, G. On a kinetic model for a simple market economy. J. Stat. Phys. 2005, 120, 253. [Google Scholar] [CrossRef] [Green Version]
- Chakraborti, A.S.; Chakrabarti, B.K. Microeconomics of the ideal gas like market models. Phys. A 2009, 388, 4151–4158. [Google Scholar] [CrossRef] [Green Version]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parolini, N.; Dedè, L.; Antonietti, P.F.; Ardenghi, G.; Manzoni, A.; Miglio, E.; Pugliese, A.; Verani, M.; Quarteroni, A. SUIHTER: A new mathematical model for COVID-19. Application to the analysis of the second epidemic outbreak in Italy. Proc. R. Soc. A 2021, 477, 20210027. [Google Scholar] [CrossRef]
- Albi, G.; Bertaglia, G.; Boscheri, W.; Dimarco, G.; Pareschi, L.; Toscani, G.; Zanella, M. Kinetic modelling of epidemic dynamics: Social contacts, control with uncertain data, and multiscale spatial dynamics. In Predicting Pandemics in a Globally Connected World; Bellomo, N., Chaplain, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1. [Google Scholar]
- Ashraf, B.N. Economic impact of government interventions during the COVID-19 pandemic: International evidence from financial markets. J. Behav. Exp. Financ. 2020, 27, 1003701. [Google Scholar] [CrossRef]
- Bonaccorsi, G.; Pierri, F.; Cinelli, M.; Flori, A.; Galeazzi, A.; Porcelli, F.; Schmidt, A.L.; Valensise, C.M.; Scala, A.; Quattrociocchi, W.; et al. Economic and social consequences of human mobility restrictions under COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 15530–15535. [Google Scholar] [CrossRef]
- Gersovitz, M.; Hammer, J.S. The economical control of infectious diseases. Econ. J. 2004, 114, 1–27. [Google Scholar] [CrossRef]
- Goenka, A.; Liu, L.; Nguyen, M.H. Infectious diseases and economic growth. J. Math. Econ. 2014, 50, 34. [Google Scholar] [CrossRef] [Green Version]
- Gozzi, N.; Tizzoni, M.; Chinazzi, M.; Ferres, L.; Vespignani, A.; Perra, N. Estimating the effect of social inequalities on the mitigation of COVID-19 across communities in Santiago de Chile. Nat. Commun. 2021, 12, 2429. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Hu, M.; Ji, Q. Financial markets under the global pandemic of COVID-19. Financ. Res. Lett. 2020, 36, 101528. [Google Scholar] [CrossRef] [PubMed]
- Deaton, A. COVID-19 and Global Income Inequality; NBER Working Paper 28392; National Bureau of Economic Research: Cambridge, MA, USA, 2021. [Google Scholar]
- von Braun, J.; Zamagni, S.; Sorondo, M.S. The moment to see the poor. Science 2020, 368, 214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. An extended SEIR model with vaccination for forecasting the COVID-19 pandemic in Saudi Arabia using an ensamble Kalman filter. Mathematics 2021, 9, 636. [Google Scholar] [CrossRef]
- Bolzoni, L.; Bonacini, E.; Soresina, C.; Groppi, M. Time-optimal control strategies in SIR epidemic models. Math. Biosci. 2017, 292, 86–96. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B.; Carbone, G.; D’Onofrio, A. Effect of seasonality on the dynamics of an imitation-based vaccination model with public health intervention. Math. Biosci. Eng. 2018, 15, 299–321. [Google Scholar] [PubMed] [Green Version]
- Buonomo, B.; Lacitignola, D.; Vargas-De-León, C. Qualitative analysis and optimal control of an epidemic model with vaccination and treatment. Math. Comput. Simul. 2014, 100, 88–102. [Google Scholar] [CrossRef]
- Buonomo, B.; Marca, R.D.; d’Onofrio, A.; Groppi, M. A behavioural modelling approach to assess the impact of COVID-19 vaccine hesitancy. J. Theor. Biol. 2022, 534, 110973. [Google Scholar] [CrossRef]
- Colombo, R.M.; Garavello, M. Optimizing vaccination strategies in an age structured SIR model. Math. Biosci. Eng. 2020, 17, 1074–1089. [Google Scholar] [CrossRef]
- Dolgin, E. COVID vaccine immunity is waning—How much does that matter? Nature 2021, 597, 606–607. [Google Scholar] [CrossRef]
- Moore, S.; Hill, E.M.; Dyson, L.; Tildesley, M.J.; Keeling, M.J. Modelling optimal vaccination strategy for SARS-CoV-2 in the UK. PLoS Comput. Biol. 2021, 17, e1008849. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Li, Y.; Teng, Z.; Zhang, T.; Lu, J. Dynamical properties in an SVEIR epidemic model with age-dependent vaccination, latency, infection, and relapse. Math. Meth. Appl. Sci. 2021, 44, 12810–12834. [Google Scholar] [CrossRef]
- Townsend, J.P.; Hassler, H.B.; Wang, Z.; Miura, S.; Singh, J.; Kumar, S.; Ruddle, N.H.; Galvani, A.P.; Dornburg, A. The durability of immunity against reinfection by SARS-CoV-2: A comparative evolutionary study. Lancet 2021, 2, E666–E675. [Google Scholar] [CrossRef]
- Pareschi, L.; Toscani, G. Interacting Multiagent Systems: Kinetic Equations & Monte Carlo Methods; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Bouchaud, J.F.; Mézard, M. Wealth condensation in a simple model of economy. Phys. A 2000, 282, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Chakraborti, A.S.; Chakrabarti, B.K. Statistical mechanics of money: How saving propensity affects its distribution. Eur. Phys. J. B 2000, 17, 167–170. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, A.; Chakrabarti, B.K.; Stinchcombe, R.B. Master equation for a kinetic model of trading market and its analytic solution. Phys. Rev. E 2005, 72, 026126. [Google Scholar] [CrossRef] [Green Version]
- Drăgulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B 2000, 17, 723–729. [Google Scholar] [CrossRef] [Green Version]
- Garibaldi, U.; Scalas, E.; Donadio, S. Statistical equilibrium in simple exchange games I: Methods of solution and application to the Bennati-Dragulescu-Yakovenko (BDY) game. Eur. Phys. J. B 2006, 53, 267–272. [Google Scholar]
- Ghosh, A.; Chatterjee, A.; Inoue, J.I.; Chakrabarti, B.K. Inequality measures in kinetic exchange models of wealth distributions. Phys. A 2016, 451, 465–474. [Google Scholar] [CrossRef] [Green Version]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Filippo, A.D.; Matteo, A.D.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Gupta, A.K. Models of wealth distributions: A perspective. In Econophysics and Sociophysics: Trends and Perspectives; Chakrabarti, B.K., Chakraborti, A., Chatterjee, A., Eds.; Wiley VHC: Weinheim, Germany, 2006; pp. 161–190. [Google Scholar]
- Düring, B.; Pareschi, L.; Toscani, G. Kinetic models for optimal control of wealth inequalities. Eur. Phys. J. B 2018, 91, 265. [Google Scholar] [CrossRef] [Green Version]
- Mantegna, R.N.; Stanley, H.E. Scaling behaviour in the dynamics of an economic index. Nature 1995, 376, 46–49. [Google Scholar] [CrossRef]
- Dimarco, G.; Perthame, B.; Toscani, G.; Zanella, M. Kinetic models for epidemic dynamics with social heterogeneity. J. Math. Biol. 2021, 83, 4. [Google Scholar] [CrossRef] [PubMed]
- Zanella, M.; Bardelli, C.; Dimarco, G.; Deandrea, S.; Perotti, P.; Azzi, M.; Figini, S.; Toscani, G. A data-driven epidemic model with social structure for understanding the COVID-19 infection on a heavily affected Italian Province. Math. Mod. Meth. Appl. Sci. 2021, 31, 2533–2570. [Google Scholar] [CrossRef]
- Bellomo, N.; Bingham, R.; Chaplain, M.A.J.; Dosi, G.; Forni, G.; Knopoff, D.A.; Lowengrub, J.; Twarock, R.; Virgillito, M.E. A multiscale model of virus pandemic: Heterogeneous interactive entities in a globally connected world. Math. Mod. Meth. Appl. Scie. 2020, 30, 1591–1651. [Google Scholar] [CrossRef]
- Loy, N.; Tosin, A. A viral load-based model for epidemic spread on spatial networks. Math. Biosci. Eng. 2021, 18, 5635–5663. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Stechlinski, P. Infectious disease models with time-varying parameters and general nonlinear incidence rate. Appl. Math. Model. 2012, 36, 1974–1994. [Google Scholar] [CrossRef]
- Britton, T.; Ball, F.; Trapman, P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science 2020, 369, 846–849. [Google Scholar] [CrossRef]
- Fumanelli, L.; Ajelli, M.; Manfredi, P.; Vespignani, A.; Merler, S. Inferring the structure of social contacts from demographic data in the analysis of infectious diseases spread. PLoS Comput. Biol. 2012, 8, e1002673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lunelli, A.; Pugliese, A.; Rizzo, C. Epidemic patch models applied to pandemic influenza: Contact matrix, stochasticity, robustness of predictions. Math. Biosci. 2009, 220, 24–33. [Google Scholar] [CrossRef]
- McCarthy, Z.; Xiao, Y.; Scarabel, F.; Tang, B.; Bragazzi, N.L.; Nah, K.; Heffernan, J.K.; Asgary, A.; Murty, V.K.; Ogden, N.H.; et al. Quantifying the shift in social contact patterns in response to non-pharmaceutical interventions. J. Math. Ind. 2020, 10, 28. [Google Scholar] [CrossRef] [PubMed]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008, 5, 0381–0391. [Google Scholar] [CrossRef] [PubMed]
- Colombo, R.M.; Garavello, M.; Marcellini, F. An age and space structured SIR model describing the COVID-19 pandemic. J. Math. Ind. 2020, 10, 22. [Google Scholar] [CrossRef] [PubMed]
- Bisi, M.; Carrillo, J.A.; Toscani, G. Contractive metrics for a Boltzmann equation for granular gases: Diffusive equilibria. J. Stat. Phys. 2005, 118, 301–331. [Google Scholar] [CrossRef]
- Cercignani, C. The Boltzmann Equation and its Applications; Springer: Berlin, Germany, 1988. [Google Scholar]
- Villani, C. On a new class of weak solutions to the spatially homogeneous Boltzmann and Landau equations. Arch. Ration. Mech. Anal. 1998, 143, 273–307. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germay, 1996; Volume 18. [Google Scholar]
- Ferrero, J.C. The monomodal, polymodal, equilibrium and nonequilibrium distribution of money. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Cernusco, Italy, 2005; pp. 159–167. [Google Scholar]
- Dolbeault, J.; Turinici, G. Social heterogeneity and the COVID-19 lockdown in a multi-group SEIR model. Comput. Math. Biophys. 2021, 9, 14–21. [Google Scholar] [CrossRef]
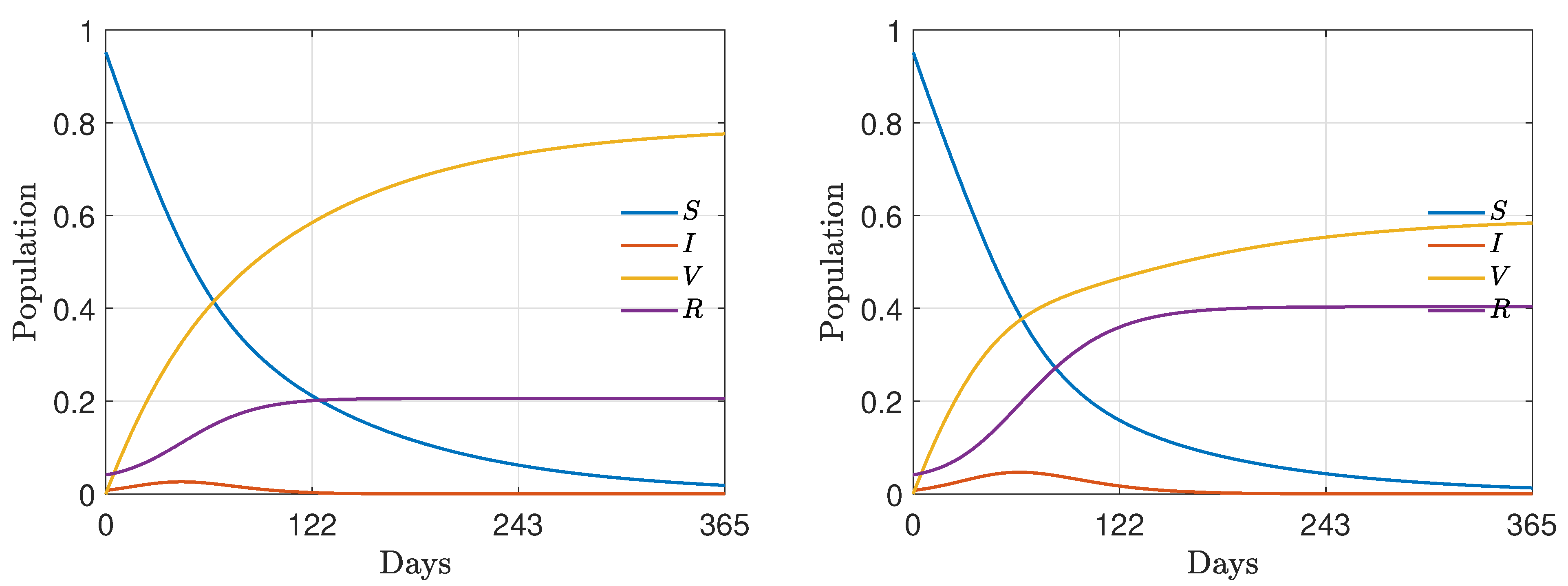





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardi, E.; Pareschi, L.; Toscani, G.; Zanella, M. Effects of Vaccination Efficacy on Wealth Distribution in Kinetic Epidemic Models. Entropy 2022, 24, 216. https://doi.org/10.3390/e24020216
Bernardi E, Pareschi L, Toscani G, Zanella M. Effects of Vaccination Efficacy on Wealth Distribution in Kinetic Epidemic Models. Entropy. 2022; 24(2):216. https://doi.org/10.3390/e24020216
Chicago/Turabian StyleBernardi, Emanuele, Lorenzo Pareschi, Giuseppe Toscani, and Mattia Zanella. 2022. "Effects of Vaccination Efficacy on Wealth Distribution in Kinetic Epidemic Models" Entropy 24, no. 2: 216. https://doi.org/10.3390/e24020216
APA StyleBernardi, E., Pareschi, L., Toscani, G., & Zanella, M. (2022). Effects of Vaccination Efficacy on Wealth Distribution in Kinetic Epidemic Models. Entropy, 24(2), 216. https://doi.org/10.3390/e24020216






