Closed-System Solution of the 1D Atom from Collision Model
Abstract
:1. Introduction
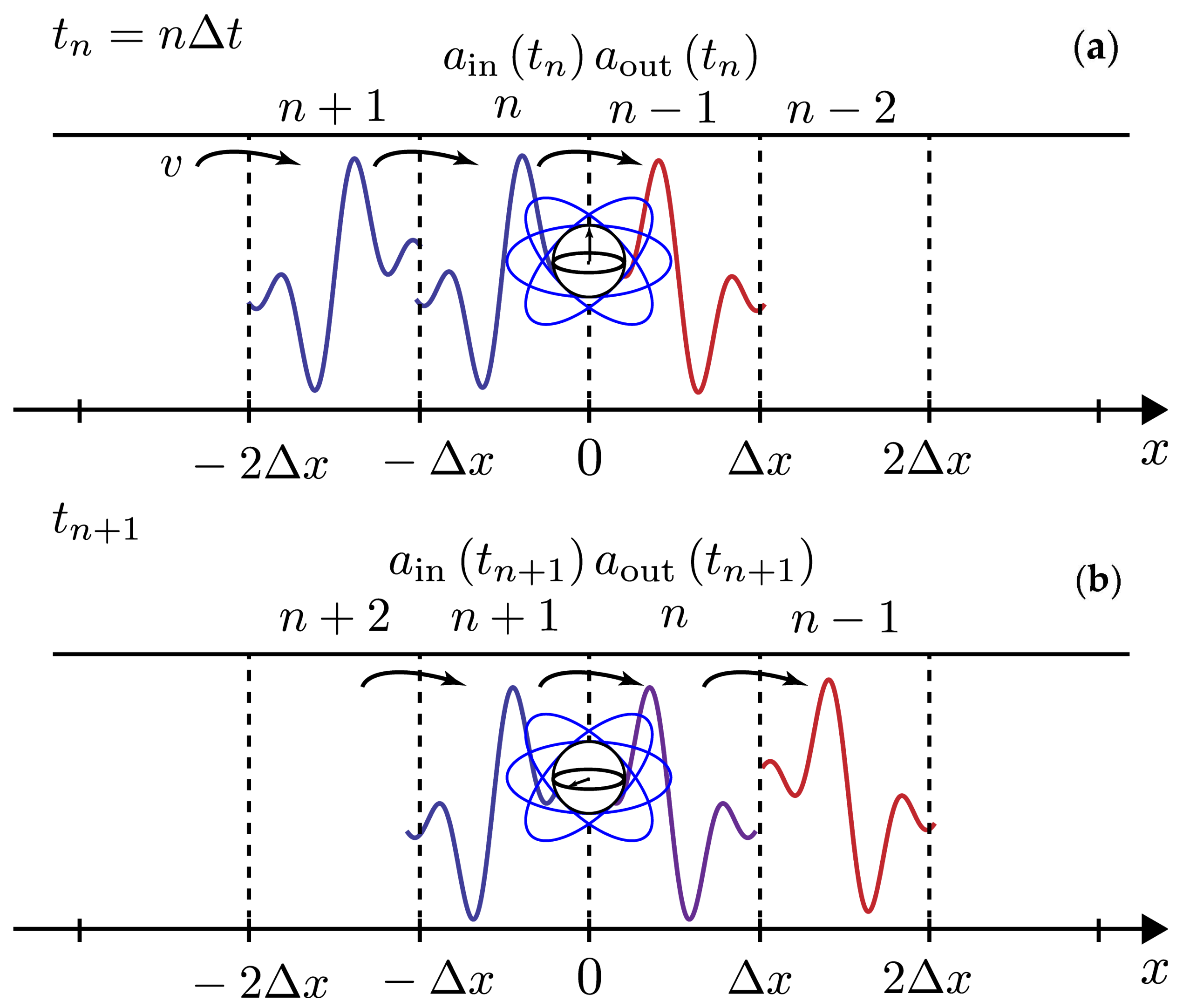
2. Collision Model of the 1D Atom
3. Closed-System Solution for the Coherent Input Field
4. Closed-System Solution for the Single-Photon Input Field
5. Conclusions
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
Abbreviations
| QED | Quantum electrodynamics |
| 1D | One-dimensional |
| CM | Collision model |
References
- Haroche, S.; Raimond, J.M. Exploring the Quantum: Atoms, Cavities and Photons; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Blais, A.; Grimsmo, A.L.; Girvin, S.M.; Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 2021, 93, 025005. [Google Scholar] [CrossRef]
- Northup, T.; Blatt, R. Quantum information transfer using photons. Nat. Photonics 2014, 8, 356–363. [Google Scholar] [CrossRef]
- Andolina, G.M.; Farina, D.; Mari, A.; Pellegrini, V.; Giovannetti, V.; Polini, M. Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys. Rev. B 2018, 98, 205423. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the Quantum Regime Fundamental Aspects and New Directions; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Sheremet, A.S.; Petrov, M.I.; Iorsh, I.V.; Poshakinskiy, A.V.; Poddubny, A.N. Waveguide quantum electrodynamics: Collective radiance and photon-photon correlations. arXiv 2021, arXiv:2103.06824. [Google Scholar]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- O’brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef] [Green Version]
- Cottet, N.; Huard, B. Maxwell’s Demon in Superconducting Circuits. arXiv 2018, arXiv:1805.01224. [Google Scholar]
- Monsel, J.; Fellous-Asiani, M.; Huard, B.; Auffèves, A. The Energetic Cost of Work Extraction. Phys. Rev. Lett. 2020, 124, 130601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elouard, C.; Herrera-Martí, D.; Esposito, M.; Auffèves, A. Thermodynamics of optical Bloch equations. New J. Phys. 2020, 22, 103039. [Google Scholar] [CrossRef]
- Maffei, M.; Camati, P.A.; Auffèves, A. Probing nonclassical light fields with energetic witnesses in waveguide quantum electrodynamics. Phys. Rev. Res. 2021, 3, L032073. [Google Scholar] [CrossRef]
- Stevens, J.; Szombati, D.; Maffei, M.; Elouard, C.; Assouly, R.; Cottet, N.; Dassonneville, R.; Ficheux, Q.; Zeppetzauer, S.; Bienfait, A.; et al. Energetics of a Single Qubit Gate. arXiv 2021, arXiv:2109.09648. [Google Scholar]
- Loredo, J.; Antón, C.; Reznychenko, B.; Hilaire, P.; Harouri, A.; Millet, C.; Ollivier, H.; Somaschi, N.; De Santis, L.; Lemaître, A.; et al. Generation of non-classical light in a photon-number superposition. Nat. Photonics 2019, 13, 803. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718, 1. [Google Scholar] [CrossRef]
- Ficheux, Q.; Jezouin, S.; Leghtas, Z.; Huard, B. Dynamics of a qubit while simultaneously monitoring its relaxation and dephasing. Nat. Commun. 2018, 9, 1926. [Google Scholar] [CrossRef]
- Aljunid, S.A.; Maslennikov, G.; Wang, Y.; Dao, H.L.; Scarani, V.; Kurtsiefer, C. Excitation of a Single Atom with Exponentially Rising Light Pulses. Phys. Rev. Lett. 2013, 111, 103001. [Google Scholar] [CrossRef] [Green Version]
- Distante, E.; Daiss, S.; Langenfeld, S.; Hartung, L.; Thomas, P.; Morin, O.; Rempe, G.; Welte, S. Detecting an Itinerant Optical Photon Twice without Destroying It. Phys. Rev. Lett. 2021, 126, 253603. [Google Scholar] [CrossRef]
- Weisskopf, V.; Wigner, E. Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie. Z. Phys. 1930, 63, 54. [Google Scholar] [CrossRef]
- Valente, D.; Arruda, M.F.Z.; Werlang, T. Non-Markovianity induced by a single-photon wave packet in a one-dimensional waveguide. Opt. Lett. 2016, 41, 3126. [Google Scholar] [CrossRef] [Green Version]
- Chumak, O.O.; Stolyarov, E.V. Phase-space distribution functions for photon propagation in waveguides coupled to a qubit. Phys. Rev. A 2013, 88, 013855. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.T.; Fan, S. Coherent photon transport from spontaneous emission in one-dimensional waveguides. Opt. Lett. 2005, 30, 2001–2003. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; Kocabaş, Ş.E.; Shen, J.T. Input–output formalism for few-photon transport in one-dimensional nanophotonic waveguides coupled to a qubit. Phys. Rev. A 2010, 82, 063821. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Shen, J.T. Photonic-Fock-state scattering in a waveguide-QED system and their correlation functions. Phys. Rev. A 2015, 92, 033803. [Google Scholar] [CrossRef] [Green Version]
- Fischer, K.A.; Trivedi, R.; Ramasesh, V.; Siddiqi, I.; Vučković, J. Scattering into one-dimensional waveguides from a coherently-driven quantum-optical system. Quantum 2018, 2, 69. [Google Scholar] [CrossRef]
- Kiilerich, A.H.; Mølmer, K. Input–Output Theory with Quantum Pulses. Phys. Rev. Lett. 2019, 123, 123604. [Google Scholar] [CrossRef] [Green Version]
- Ciccarello, F.; Lorenzo, S.; Giovannetti, V.; Palma, G.M. Quantum collision models: Open system dynamics from repeated interactions. arXiv 2021, arXiv:2106.11974. [Google Scholar]
- Ciccarello, F.; Palma, G.M.; Giovannetti, V. Collision-model-based approach to non-Markovian quantum dynamics. Phys. Rev. A 2013, 87, 040103. [Google Scholar] [CrossRef]
- Rybár, T.; Filippov, S.N.; Ziman, M.; Bužek, V. Simulation of indivisible qubit channels in collision models. J. Phys. At. Mol. Opt. Phys. 2012, 45, 154006. [Google Scholar] [CrossRef] [Green Version]
- Ciccarello, F. Collision models in quantum optics. Quantum Meas. Quantum Metrol. 2017, 4, 53. [Google Scholar] [CrossRef] [Green Version]
- Cilluffo, D.; Carollo, A.; Lorenzo, S.; Gross, J.A.; Palma, G.M.; Ciccarello, F. Collisional picture of quantum optics with giant emitters. Phys. Rev. Res. 2020, 2, 043070. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and Atoms-Introduction to Quantum Electrodynamics; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Gardiner, C.W.; Collett, M.J. Input and output in damped quantum systems: Quantum stochastic differential equations and the master equation. Phys. Rev. A 1985, 31, 3761. [Google Scholar] [CrossRef]
- Gross, J.A.; Caves, C.M.; Milburn, G.J.; Combes, J. Qubit models of weak continuous measurements: Markovian conditional and open-system dynamics. Quantum Sci. Technol. 2018, 3, 024005. [Google Scholar] [CrossRef] [Green Version]
- Magnus, W. On the exponential solution of differential equations for a linear operator. Commun. Pure Appl. Math. 1954, 7, 649–673. [Google Scholar] [CrossRef]
- Gheri, K.M.; Ellinger, K.; Pellizzari, T.; Zoller, P. Photon-Wavepackets as Flying Quantum Bits. Fortschritte Phys. Prog. Phys. 1998, 46, 401–415. [Google Scholar] [CrossRef]
- Dąbrowska, A.; Chruściński, D.; Chakraborty, S.; Sarbicki, G. Eternally non-Markovian dynamics of a qubit interacting with a single-photon wavepacket. New J. Phys. 2021, 23, 123019. [Google Scholar] [CrossRef]
- Landi, G.T.; Paternostro, M. Irreversible entropy production: From classical to quantum. Rev. Mod. Phys. 2021, 93, 035008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maffei, M.; Camati, P.A.; Auffèves, A. Closed-System Solution of the 1D Atom from Collision Model. Entropy 2022, 24, 151. https://doi.org/10.3390/e24020151
Maffei M, Camati PA, Auffèves A. Closed-System Solution of the 1D Atom from Collision Model. Entropy. 2022; 24(2):151. https://doi.org/10.3390/e24020151
Chicago/Turabian StyleMaffei, Maria, Patrice A. Camati, and Alexia Auffèves. 2022. "Closed-System Solution of the 1D Atom from Collision Model" Entropy 24, no. 2: 151. https://doi.org/10.3390/e24020151
APA StyleMaffei, M., Camati, P. A., & Auffèves, A. (2022). Closed-System Solution of the 1D Atom from Collision Model. Entropy, 24(2), 151. https://doi.org/10.3390/e24020151





