Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source
Abstract
1. Introduction
2. Design of the Random Number Generator
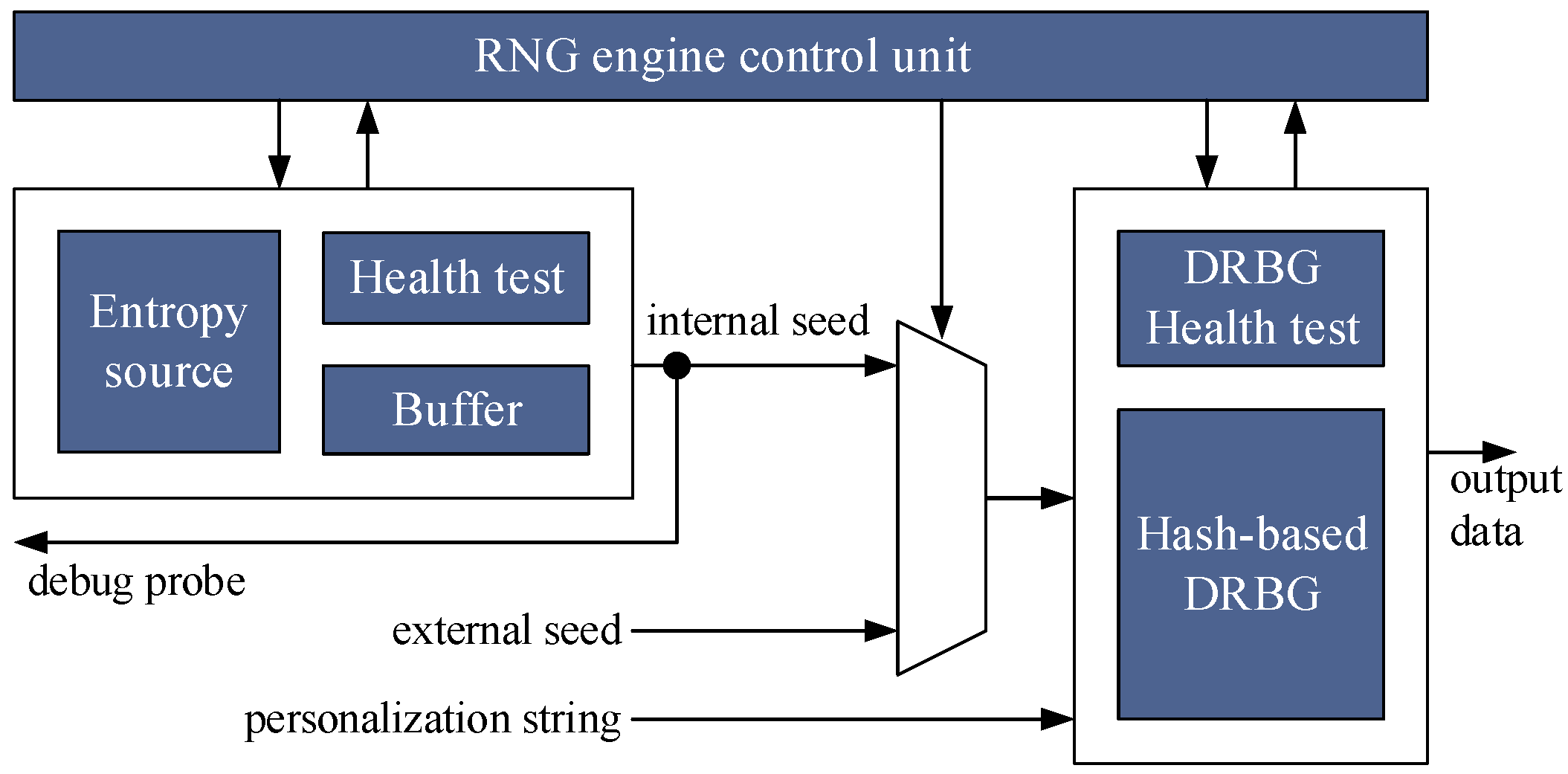
2.1. RNG Engine
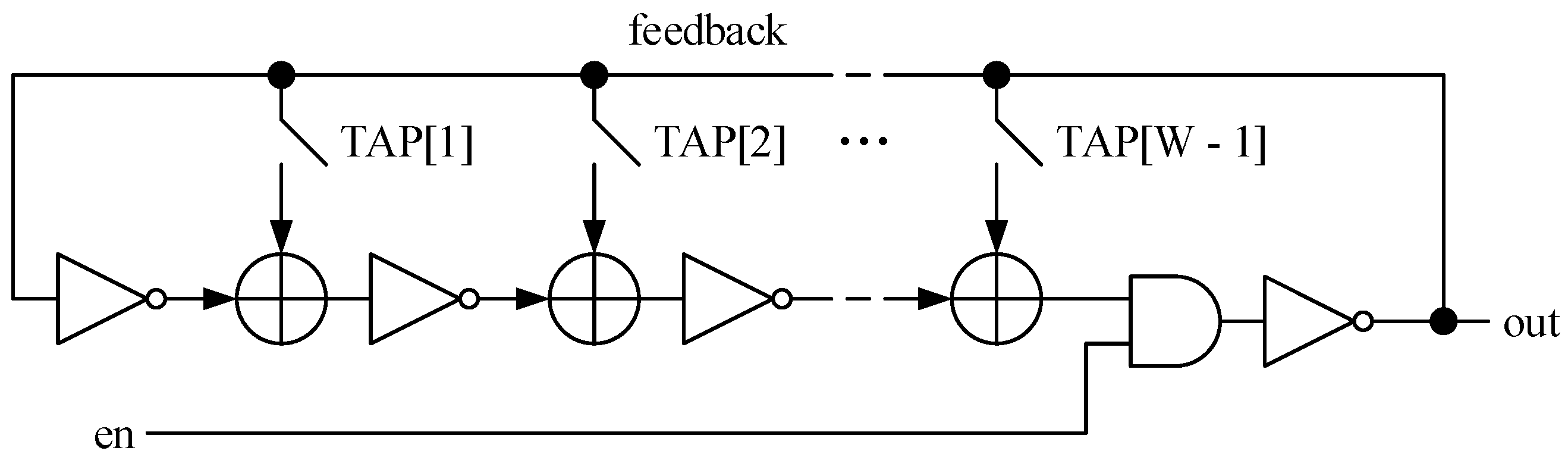
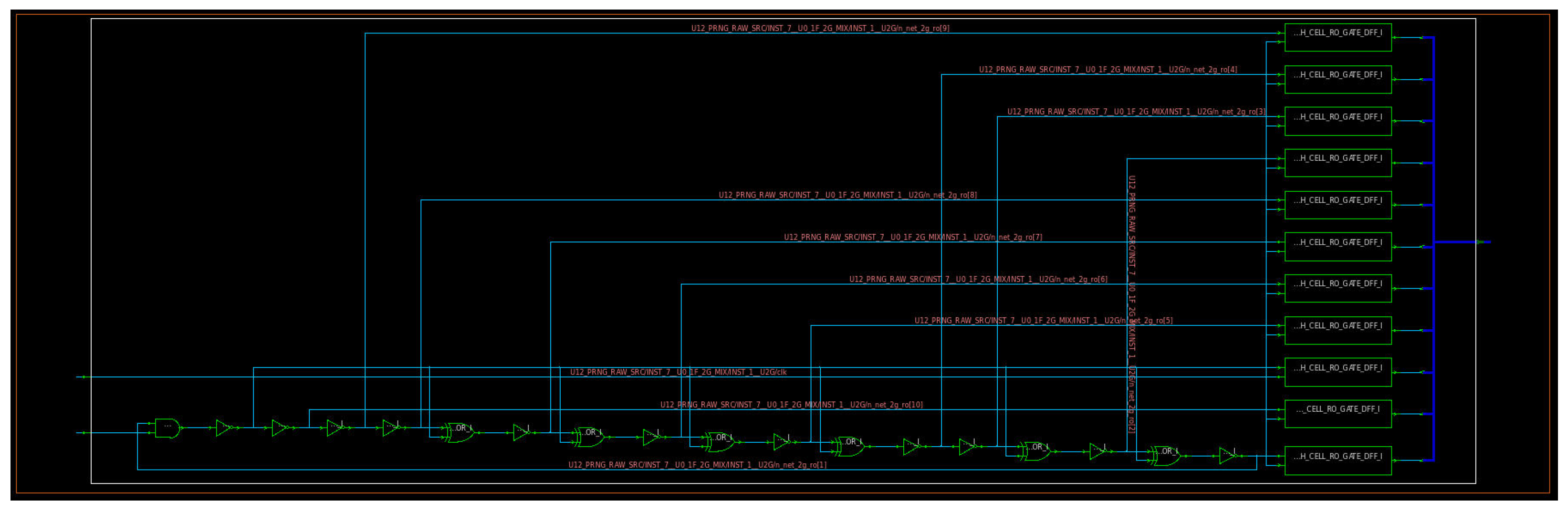
2.2. Entropy and Design of the All-Digital Entropy Source
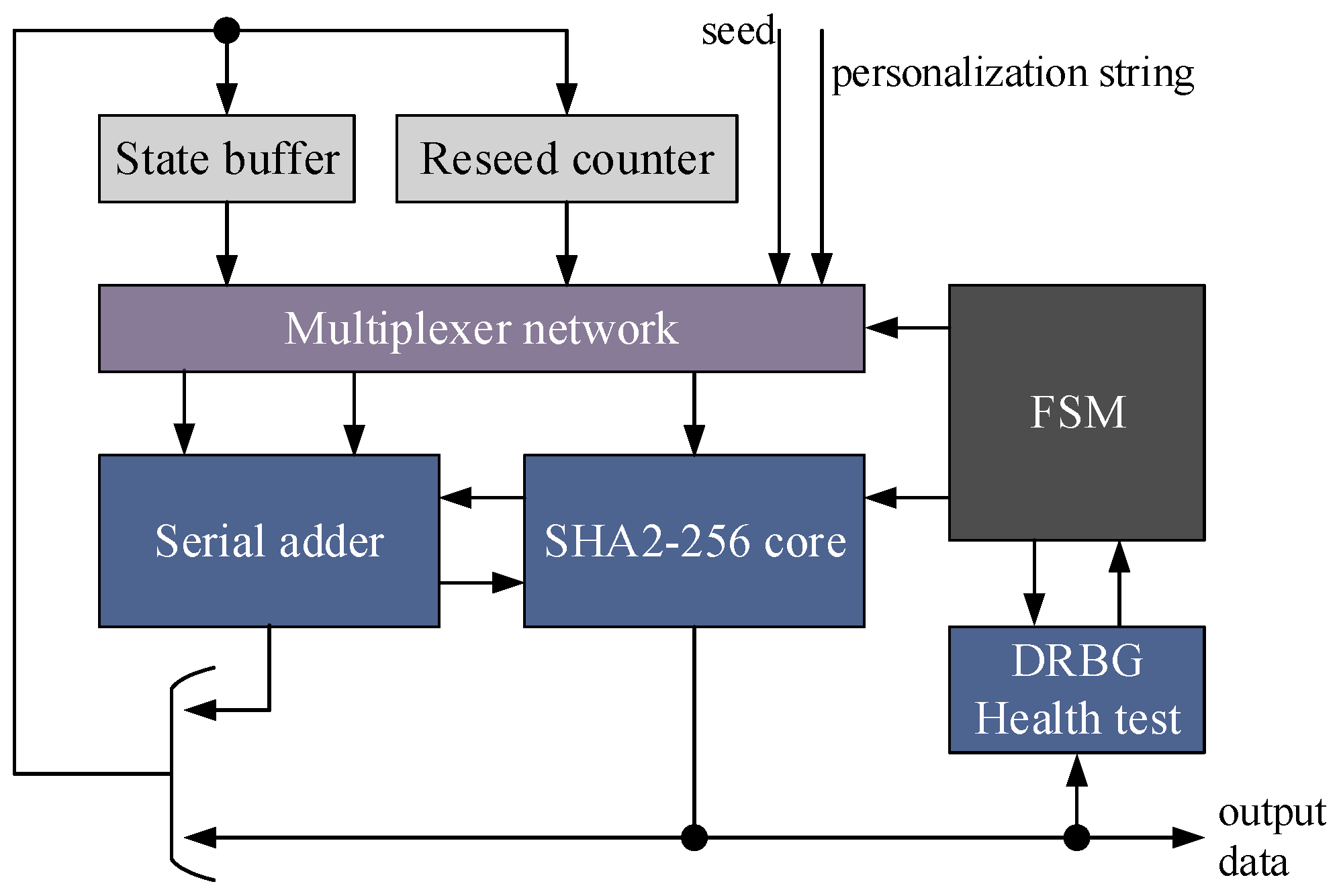
2.3. Design of the Deterministic Random Bit Generator Module
- CTR-DRBG, which relies on the CTR mode of operation of block ciphers;
- HMAC-DRBG, which relies on the HMAC scheme of hash algorithms.
- , for the SHA2-256 case;
- , for the SHA2-512 case.
2.4. Synthesis Design
3. Results
3.1. Results on FPGA and 7 nm Standard Cell Technologies
3.2. RNG Assessment
- The batteries of tests PractRand [26], employed in [27,28], and TestU01 [29], whose usage is reported in [27,28,30,31,32,33]: both essentially represent an enhancement of Diehard(er) suite, because they include some improvements such as the possibility of setting the parameters of some of the offered statical tests (feature not offered by Diehard(er));
3.2.1. Entropy Evaluation
- bits of entropy per byte, corresponding to bit of entropy per bit, estimated with the NIST EA suite;
- bits of entropy per byte, corresponding to bit of entropy per bit, estimated with the BSI suite.
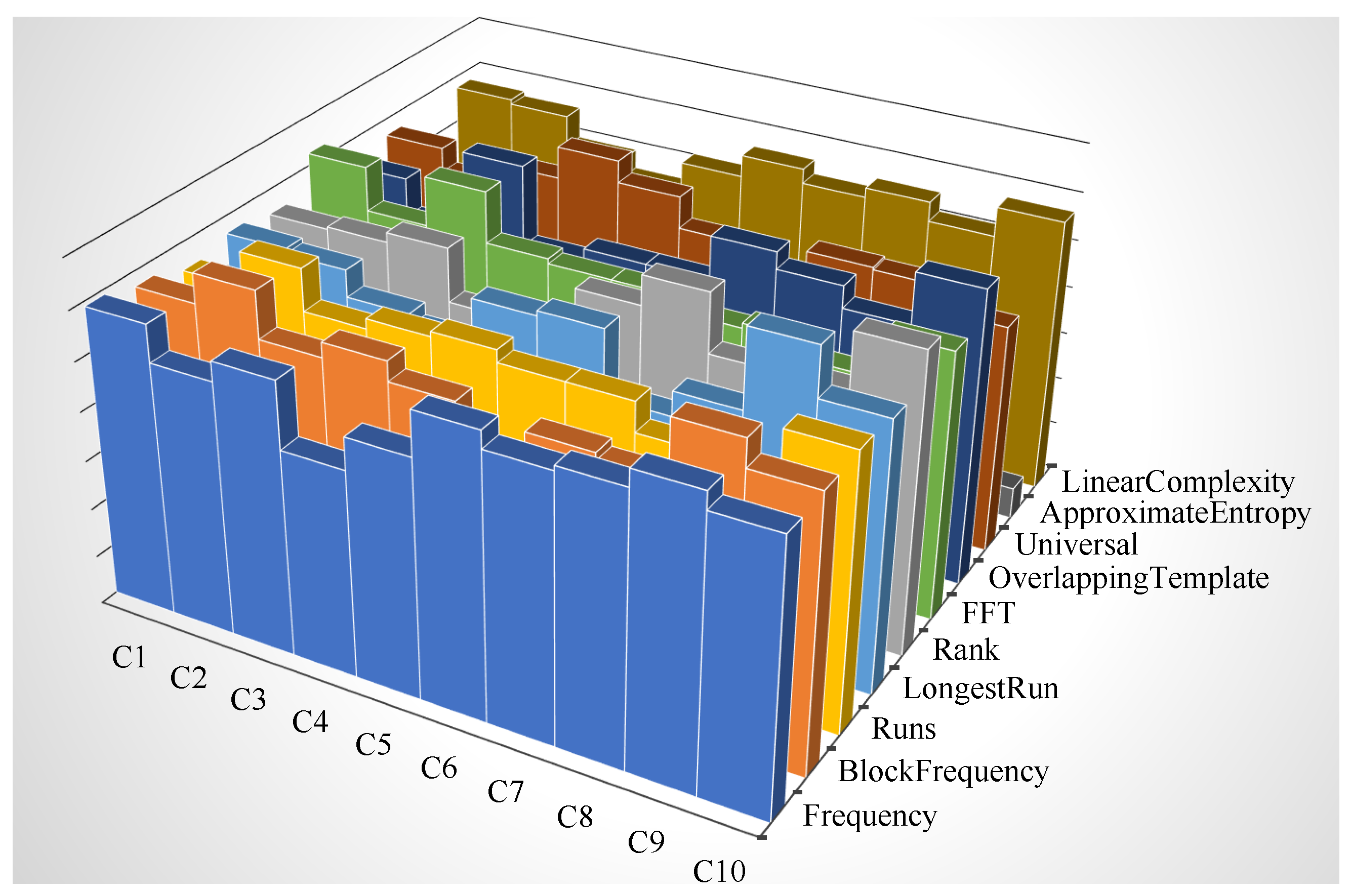
3.2.2. Randomness Tests
- The p-value of each sequence is calculated, discarding the sequences for which p-value < ;
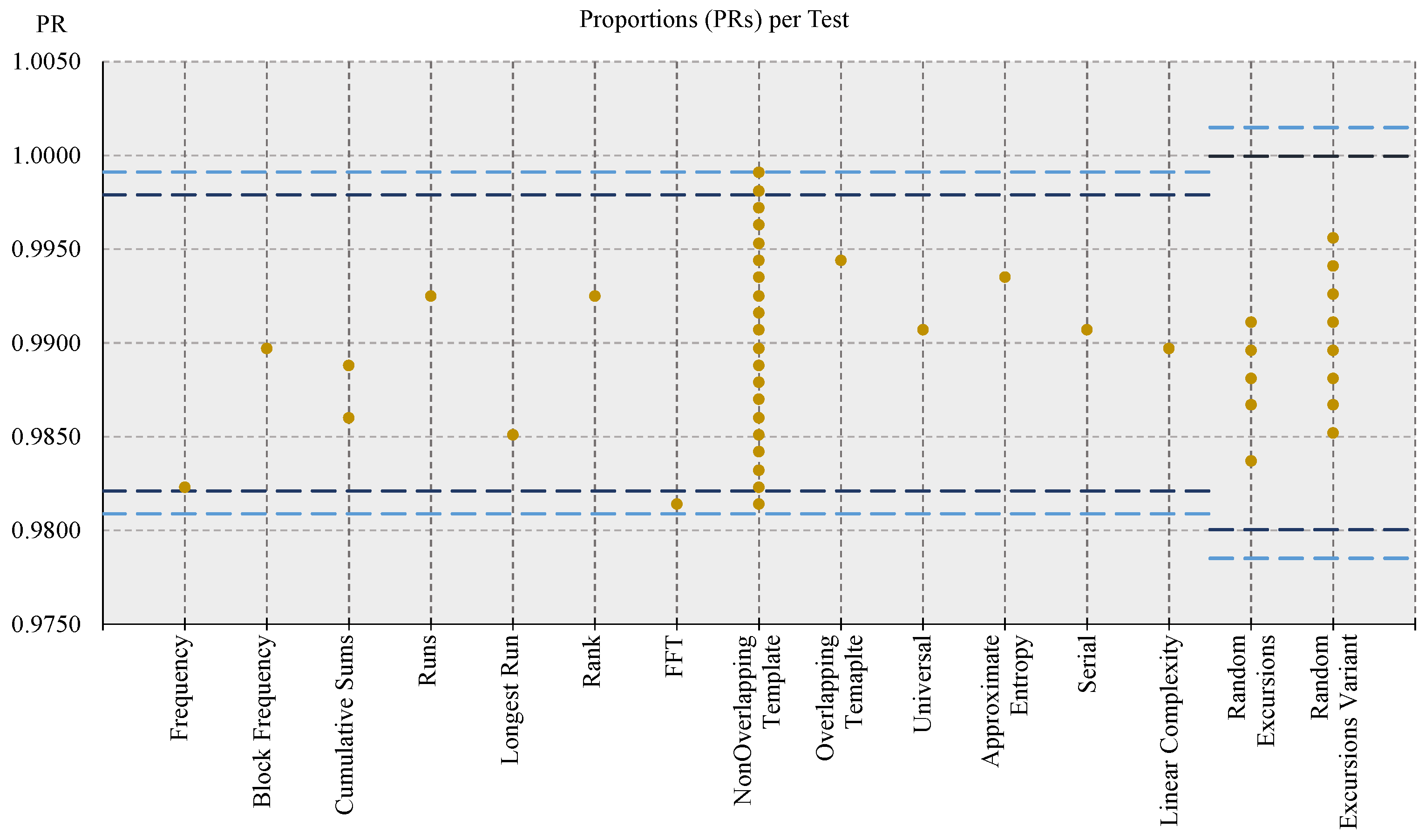
- The ratio between the number of sequences that passed the test (i.e., the one for p-value ) and the total number of tested sequences (i.e., k) is computed, and it is labeled as PRoportion (PR);
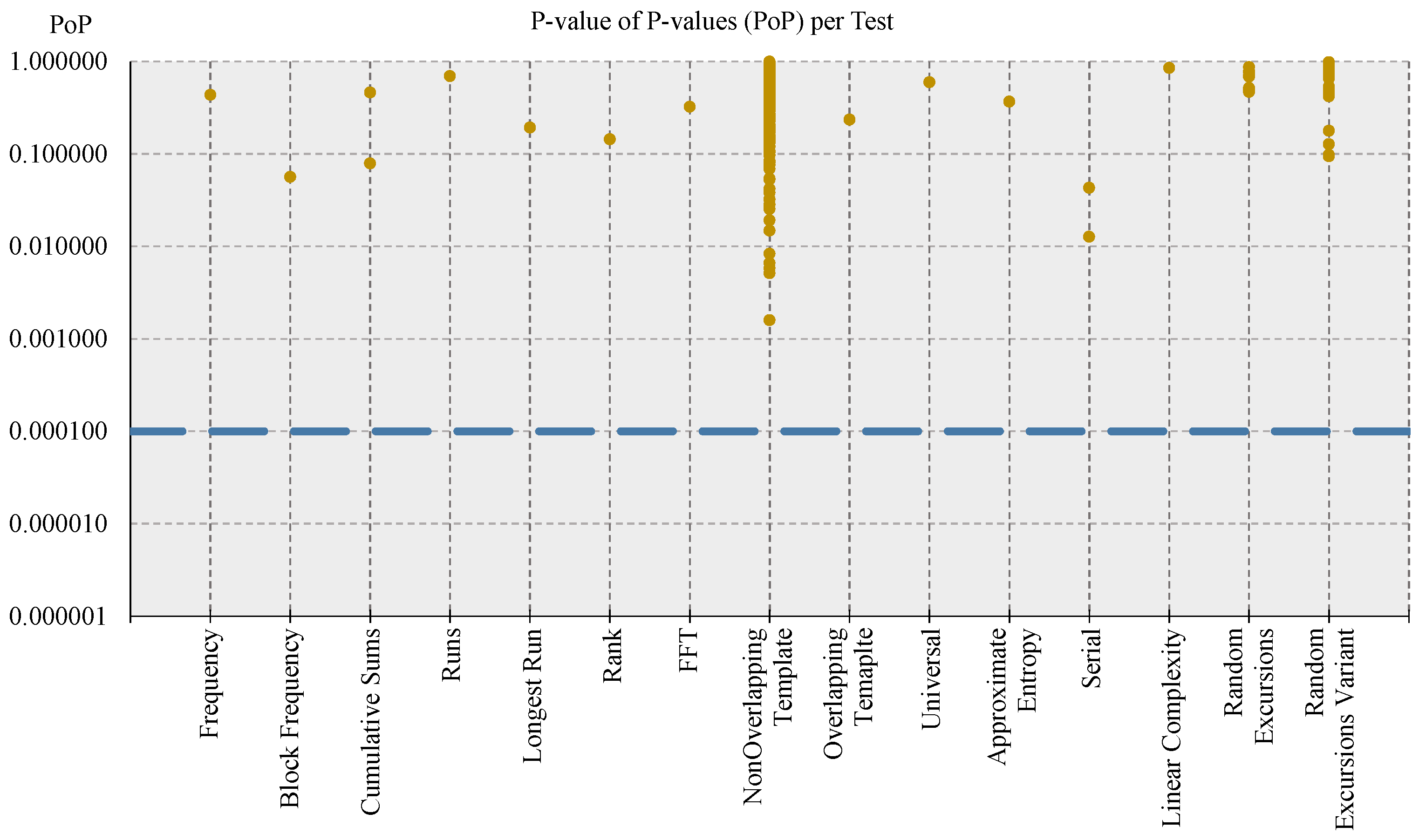
- The p-value of sequences that passed the test are distributed in the range by splitting it into 10 equal sub-intervals, and the uniformity of the distribution of p-value is calculated: basing on the chi-square (chi-squared or ) function, the uniformity of distribution is determined by computing a figure that can be considered as a p-value of p-value (PoP);
- For each test, PR lies in the confidence interval defined as ;
- For each test, PoP ≥ 0.0001 (i.e., the p-values of sequences that passed the test are uniformly distributed).
4. Comparison to the State of the Art
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Consortium, E. EPI Website. Available online: https://www.european-processor-initiative.eu/ (accessed on 10 December 2021).
- Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Zulberti, L.; Saponara, S.; Fanucci, L. VLSI design of Advanced-Features AES CryptoProcessor in the framework of the European Processor Initiative. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, in press. [Google Scholar] [CrossRef]
- Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Nannipieri, P.; Fanucci, L.; Saponara, S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies 2021, 14, 4676. [Google Scholar] [CrossRef]
- Nannipieri, P.; Bertolucci, M.; Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Falaschi, F.; Fanucci, L.; Saponara, S. SHA2 and SHA-3 Accelerator Design in a 7 nm Technology within the European Processor Initiative. Microprocess. Microsyst. 2020, 87, 103444, in press. [Google Scholar] [CrossRef]
- Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Belli, J.; Fanucci, L.; Saponara, S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Appl. Sci. 2021, 11, 3330. [Google Scholar] [CrossRef]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Belli, J.; Fanucci, L.; Saponara, S. Digital Random Number Generator Hardware Accelerator IP-Core for Security Applications. In Applications in Electronics Pervading Industry, Environment and Society. ApplePies 2019; Lecture Notes in Electrical Engineering (LNEE); Springer: Berlin/Heidelberg, Germany, 2020; Volume 627, pp. 117–123. [Google Scholar] [CrossRef][Green Version]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Bertolucci, M.; Belli, J.; Fanucci, L.; Saponara, S. Cryptographically Secure Pseudo-Random Number Generator IP-Core Based on SHA2 Algorithm. Sensors 2020, 20, 1869. [Google Scholar] [CrossRef]
- NIST. Recommendation for Random Number Generation Using Deterministic Random Bit Generators; SP 800-90A Rev. 1; NIST: Gaithersburg, MD, USA, 2015.
- NIST. Recommendation for Random Bit Generator (RBG) Constructions; SP 800-90C (Draft); NIST: Gaithersburg, MD, USA, 2016.
- Varchola, M.; Drutarovsky, M. New High Entropy Element for FPGA Based True Random Number Generators. In Cryptographic Hardware and Embedded Systems (CHES) 2010; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2010; Volume 6225, pp. 351–365. [Google Scholar]
- Vasyltsov, I.; Hambardzumyan, E.; Kim, Y.S.; Karpinskyy, B. Fast Digital TRNG Based on Metastable Ring Oscillator. In Cryptographic Hardware and Embedded Systems (CHES) 2008; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2008; Volume 5154, pp. 164–180. [Google Scholar]
- Schramm, M.; Dojen, R.; Heigl, M. Experimental assessment of FIRO- and GARO-based noise sources for digital TRNG designs on FPGAs. In Proceedings of the 2017 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 5–6 September 2017; pp. 1–6. [Google Scholar]
- Demir, K.; Ergün, S. A Comparative Study on Fibonacci-Galois Ring Oscillators for Random Number Generation. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 9–12 August 2020; pp. 631–634. [Google Scholar]
- Cao, Y.; Rožić, V.; Yang, B.; Balasch, J.; Verbauwhede, I. Exploring active manipulation attacks on the TERO random number generator. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar]
- Li, T.; Wu, L.; Zhang, X.; Wu, X.; Zhou, J.; Wang, X. A Novel Transition Effect Ring Oscillator Based True Random Number Generator for a Security SoC. In Proceedings of the 2017 International Conference on Electron Devices and Solid-State Circuits (EDSSC), Hsinchu, Taiwan, 18–20 October 2017; pp. 1–2. [Google Scholar]
- Fujieda, N. On the Feasibility of TERO-Based True Random Number Generator on Xilinx FPGAs. In Proceedings of the 2020 30th International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 31 August–4 September 2020; pp. 103–108. [Google Scholar]
- Kan, W. Analysis of Underlying Assumptions in NIST DRBGs. In IACR Cryptology ePrint Archive; IACR: Lyon, France, 2007; p. 345. [Google Scholar]
- Synopsys. Design Compiler. Available online: https://www.synopsys.com/support/training/rtl-synthesis.html (accessed on 10 December 2021).
- Xilinx. Vivado. Available online: https://www.xilinx.com/products/design-tools/vivado/implementation.html (accessed on 10 December 2021).
- Xilinx. UltraScale+ FPGAs—Product Tables and Product Selection Guide. 2015–2021. Available online: https://www.xilinx.com/support/documentation/selection-guides/ultrascale-plus-fpga-product-selection-guide.pdf (accessed on 10 December 2021).
- Brown, R. Dieharder: A Random Number Test Suite. Version 3.31.1. 2004. Available online: https://webhome.phy.duke.edu/~rgb/General/dieharder.php (accessed on 10 December 2021).
- Walker, J. ENT—A Pseudorandom Number Sequence Test Program. Available online: https://www.fourmilab.ch/random/ (accessed on 10 December 2021).
- Aggarwal, D.; Ghatikar, R.; Chennuri, S.; Banerjee, A. Generation of 1 Gb full entropy random numbers with the enhanced-NRBG method. arXiv 2021, arXiv:2108.04331. [Google Scholar]
- Sun, Y.; Lo, B. Random number generation using inertial measurement unit signals for on-body IoT devices. In Proceedings of the Living in the Internet of Things: Cybersecurity of the IoT-2018, London, UK, 28–29 March 2018; pp. 1–9. [Google Scholar] [CrossRef]
- PractRand (Practically Random) C++ Library. Available online: http://pracrand.sourceforge.net/ (accessed on 10 December 2021).
- Gevorkyan, M.N.; Demidova, A.; Korol’kova, A.; Kulyabov, D. A Practical Approach to Testing Random Number Generators in Computer Algebra Systems. Comput. Math. Math. Phys. 2020, 60, 65–73. [Google Scholar] [CrossRef]
- Sleem, L.; Couturier, R. TestU01 and Practrand: Tools for a randomness evaluation for famous multimedia ciphers. Multimed. Tools Appl. 2020, 79, 24075–24088. [Google Scholar] [CrossRef]
- L’Ecuyer, P.; Simard, R. TestU01: AC library for empirical testing of random number generators. ACM Trans. Math. Softw. (TOMS) 2007, 33, 1–40. [Google Scholar] [CrossRef]
- Bisadi, Z.; Fontana, G.; Moser, E.; Pucker, G.; Pavesi, L. Robust Quantum Random Number Generation with Silicon Nanocrystals Light Source. J. Light. Technol. 2017, 35, 1588–1594. [Google Scholar] [CrossRef]
- Bakiri, M.; Couchot, J.F.; Guyeux, C. CIPRNG: A VLSI Family of Chaotic Iterations Post-Processings for -Linear Pseudorandom Number Generation Based on Zynq MPSoC. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1628–1641. [Google Scholar] [CrossRef]
- Chen, S.; Yu, S.; Lü, J.; Chen, G.; He, J. Design and FPGA-Based Realization of a Chaotic Secure Video Communication System. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2359–2371. [Google Scholar] [CrossRef]
- Sharipov, B.R.; Perukhin, M.Y.; Mullayanov, B.I. Statistical Analysis of Pseudorandom Sequences and Stegocontainers. In Proceedings of the 2021 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 17–21 May 2021; pp. 434–439. [Google Scholar] [CrossRef]
- NIST. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; SP 800-22; NIST: Gaithersburg, MA, USA, 2010.
- Killmann, W.; Schindler, W. A Proposal for: Functionality Classes for Random Number Generators, Version 2.0; Mathematical-Technical Reference of AIS 20/31; NIST: Gaithersburg, MA, USA, 2011.
- BSI. Functionality Classes and Evaluation Methodology for Deterministic Random Number Generators; Version 1; AIS 20; BSI: Bonn, Germany, 1999. [Google Scholar]
- BSI. Functionality Classes and Evaluation Methodology for Physical Random Number Generators; Version 1; AIS 31; BSI: Bonn, Germany, 2001. [Google Scholar]
- Zhang, M.; Zhang, X.; Zhu, Y.; Miao, S. Overview of Randomness Test on Cryptographic Algorithms. J. Phys. Conf. Ser. IOP Publ. 2021, 1861, 012009. [Google Scholar]
- Petura, O.; Mureddu, U.; Bochard, N.; Fischer, V.; Bossuet, L. A Survey of AIS-20/31 Compliant TRNG Cores Suitable for FPGA Devices. In Proceedings of the 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, 29 August–2 September 2016. [Google Scholar]
- Demirhan, H.; Bitirim, N. Statistical testing of cryptographic randomness. İstat. Derg. İstat. Aktüerya 2016, 9, 1–11. [Google Scholar]
- Balasch, J.; Bernard, F.; Fischer, V.; Grujić, M.; Laban, M.; Petura, O.; Rožić, V.; Van Battum, G.; Verbauwhede, I.; Wakker, M.; et al. Design and Testing Methodologies for True Random Number Generators Towards Industry Certification. In Proceedings of the 2018 IEEE 23rd European Test Symposium (ETS), Bremen, Germany, 28 May–1 June 2018; pp. 1–10. [Google Scholar]
- BSI. Implementation of Test Procedure A and Test Procedure B for AIS 20/31 Standard. Available online: https://www.bsi.bund.de/SharedDocs/Downloads/DE/BSI/Zertifizierung/Interpretationen/AIS_31_testsuit_zip.zip (accessed on 10 December 2021).
- Schindler, W. AIS 20: Functionality Classes and Evaluation Methodology for Deterministic Random Number Generators; Version 2.0; Mathematical-Technical Reference of AIS 20; BSI: Bonn, Germany, 1999. [Google Scholar]
- Killmann, W.; Schindler, W. A Proposal for: Functionality Classes and Evaluation Methodology for True (Physical) Random Number Generators; Version 3.1; Mathematical-Technical Reference of AIS 31; BSI: Bonn, Germany, 2001. [Google Scholar]
- NIST. Recommendation for the Entropy Sources Used for Random Bit Generation; SP 800-90B; NIST: Gaithersburg, MD, USA, 2018.
- NIST. SP 800-90B Entropy Assessment Software, Version 1.0. 2019. Available online: https://github.com/usnistgov/SP800-90B_EntropyAssessment (accessed on 10 December 2021).
- NIST. SP 800-22 STS Software, Version 2.1.1. 2010. Available online: https://csrc.nist.gov/CSRC/media/Projects/Random-Bit-Generation/documents/sts-2_1_2.zip (accessed on 10 December 2021).
- Kim, Y.; Guyot, C.; Kim, Y.S. On the Efficient Estimation of Min-Entropy. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3013–3025. [Google Scholar] [CrossRef]
- Kelsey, J.; McKay, K.A.; Turan, M.S. Predictive Models for Min-Entropy Estimation. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9293, pp. 373–392. [Google Scholar]
- Sýs, M.; Riha, Z.; Matyas, V.; Marton, K.; Suciu, A. On the Interpretation of Results from the NIST Statistical Test Suite. Rom. J. Inf. Sci. Technol. (ROMJIST) 2015, 18, 18–32. [Google Scholar]
- Intel. Cyclone V Device Overview. 2018. Available online: https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/hb/cyclone-v/cv_51001.pdf (accessed on 10 December 2021).
- Xilinx. Spartan-6 FPGAs: Performance, Power, and I/O Optimized for Cost-Sensitive Applications; Technical Report; Xilinx: San Jose, CA, USA, 2017; Available online: https://www.xilinx.com/support/documentation/white_papers/wp396_S6_HV_Perf_Power.pdf (accessed on 10 December 2021).
- Microsemi. User Guide SmartFusion2 and IGLOO2 FPGA Security and Best Practices (UG0443), Revision 10.0. 2019. Available online: https://www.microsemi.com/document-portal/doc_download/132037-ug0443-smartfusion2-and-igloo2-fpga-security-best-practices-user-guide (accessed on 10 December 2021).
- Baudet, M.; Lubicz, D.; Micolod, J.; Tassiaux, A. On the Security of Oscillator-Based Random Number Generators. J. Cryptol. 2011, 24, 398–425. [Google Scholar] [CrossRef]
- Kohlbrenner, P.; Gaj, K. An Embedded True Random Number Generator for FPGAs. In Proceedings of the 12th International Symposium on Field Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2004; pp. 71–78. [Google Scholar]
- Sunar, B.; Martin, W.J.; Stinson, D.R. A Provably Secure True Random Number Generator with Built-In Tolerance to Active Attacks. IEEE Trans. Comput. 2007, 56, 109–119. [Google Scholar] [CrossRef]
- Wold, K.; Tan, C.H. Analysis and Enhancement of Random Number Generator in FPGA Based on Oscillator Rings. In Proceedings of the 2008 International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 3–5 December 2008; pp. 385–390. [Google Scholar]
- Bochard, N.; Bernard, F.; Fischer, V.; Valtchanov, B. True-Randomness and Pseudo-Randomness in Ring Oscillator-Based True Random Number Generators. Int. J. Reconfig. Comput. 2010, 2010, 879281. [Google Scholar] [CrossRef]
- Fischer, V.; Drutarovskỳ, M. True Random Number Generator Embedded in Reconfigurable Hardware. In Cryptographic Hardware and Embedded Systems (CHES) 2002; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2002; Volume 2523, pp. 415–430. [Google Scholar]
- Bernard, F.; Fischer, V.; Valtchanov, B. Mathematical Model of Physical RNGs Based on Coherent Sampling. Tatra Mt.-Math. Publ. 2010, 45, 1–14. [Google Scholar] [CrossRef]
- Haddad, P.; Fischer, V.; Bernard, F.; Nicolai, J. A Physical Approach for Stochastic Modeling of TERO-Based TRNG. In Cryptographic Hardware and Embedded Systems (CHES) 2015; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9293, pp. 357–372. [Google Scholar]
- Cherkaoui, A.; Fischer, V.; Aubert, A.; Fesquet, L. A Self-Timed Ring Based True Random Number Generator. In Proceedings of the 2013 IEEE 19th International Symposium on Asynchronous Circuits and Systems, Santa Monica, CA, USA, 19–22 May 2013; pp. 99–106. [Google Scholar]
- Cherkaoui, A.; Fischer, V.; Fesquet, L.; Aubert, A. A Very High Speed True Random Number Generator with Entropy Assessment. In Cryptographic Hardware and Embedded Systems (CHES) 2013; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2013; Volume 8086, pp. 179–196. [Google Scholar]
- Intel. Overview for the Stratix IV Device Family. In Stratix IV Device Handbook; 2020; Volume 1, Available online: https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/hb/stratix-iv/stx4_siv51001.pdf (accessed on 10 December 2021).
- Peetermans, A.; Rozic, V.; Verbauwhede, I. A Highly-Portable True Random Number Generator Based on Coherent Sampling. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–9 September 2019; pp. 218–224. [Google Scholar]


| Design Strategy | Physical Phenomena Generating Entropy | Main Characteristics |
|---|---|---|
| TERO | Latches oscillatory metastability | Low throughputs, large dependence on placement of logic cells |
| Meta-RO | Analogue metastability of inverter gates | PLL required, dependence on placement of logic cells |
| FiRO | Jitter and metastability | Good independence from placing |
| GaRO | Jitter and metastability | Good independence from placing |
| FiGaRO | Jitter and metastability | Independence from placing, higher entropy and robustness respect to single FiRO and GaRO |
| B | A | ||
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| Entity | Frequency [MHz] | CLB (162,960) | CLB LUTs (1,303,680) | CLB Registers (2,607,360) |
|---|---|---|---|---|
| RNG engine | 260 | 2151 | 9842 | 7121 |
| Entropy Source | 260 | 384 | 1567 | 2137 |
| DRBG | 260 | 1528 | 7327 | 3685 |
| Entity | Frequency [GHz] | Area [kGE] |
|---|---|---|
| RNG engine | 4.325 | 127.16 |
| Entropy Source | 4.325 | 69.29 |
| DRBG | 4.325 | 46.51 |
| True Situation | Conclusion | |
|---|---|---|
| Data Are Random (Accept H0) | Data Are Not Random (Accept Ha) | |
| Data are random (H0 is true) | No error | Type I error |
| Data are not random (Ha is true) | Type II error | No error |
| Implementation | FPGA | Bit Rate [Mbit/s] | Entropy per Bit (from BSI Suite) | Entropy Rate [Mbit/s] |
|---|---|---|---|---|
| This work | Virtex Ultrascale+ VU37P | 2080 | 0.999 | 2077.92 |
| [54] | Spartan 6 | 0.0042 | 0.999 | 0.004 |
| Cyclone V | 0.0027 | 0.990 | 0.003 | |
| SmartFusion 2 | 0.014 | 0.980 | 0.013 | |
| [55] | Spartan 6 | 0.54 | 0.999 | 0.539 |
| Cyclone V | 1.44 | 0.999 | 1.438 | |
| SmartFusion 2 | 0.328 | 0.999 | 0.327 | |
| [56,57,58] | Spartan 6 | 2.57 | 0.999 | 2.567 |
| Cyclone V | 2.2 | 0.999 | 2.197 | |
| SmartFusion 2 | 3.62 | 0.999 | 3.616 | |
| [59,60] | Spartan 6 | 0.44 | 0.981 | 0.431 |
| Cyclone V | 0.6 | 0.986 | 0.592 | |
| SmartFusion 2 | 0.37 | 0.921 | 0.340 | |
| [11,61] | Spartan 6 | 0.625 | 0.999 | 0.624 |
| Cyclone V | 1 | 0.987 | 0.985 | |
| SmartFusion 2 | 1 | 0.999 | 0.999 | |
| [62,63] | Spartan 6 | 154 | 0.998 | 154.121 |
| Cyclone V | 245 | 0.999 | 244.755 | |
| SmartFusion 2 | 188 | 0.999 | 188.522 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crocetti, L.; Di Matteo, S.; Nannipieri, P.; Fanucci, L.; Saponara, S. Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source. Entropy 2022, 24, 139. https://doi.org/10.3390/e24020139
Crocetti L, Di Matteo S, Nannipieri P, Fanucci L, Saponara S. Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source. Entropy. 2022; 24(2):139. https://doi.org/10.3390/e24020139
Chicago/Turabian StyleCrocetti, Luca, Stefano Di Matteo, Pietro Nannipieri, Luca Fanucci, and Sergio Saponara. 2022. "Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source" Entropy 24, no. 2: 139. https://doi.org/10.3390/e24020139
APA StyleCrocetti, L., Di Matteo, S., Nannipieri, P., Fanucci, L., & Saponara, S. (2022). Design and Test of an Integrated Random Number Generator with All-Digital Entropy Source. Entropy, 24(2), 139. https://doi.org/10.3390/e24020139









