On the Quantization of AB Phase in Nonlinear Systems
Abstract
:1. Introduction
2. Hamiltonian and Energy Spectrum
3. Dynamics of Adiabatic Following
4. Mechanism of the Jump of AB Phase at for Kerr Nonlinearity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Eigenvalue Problem
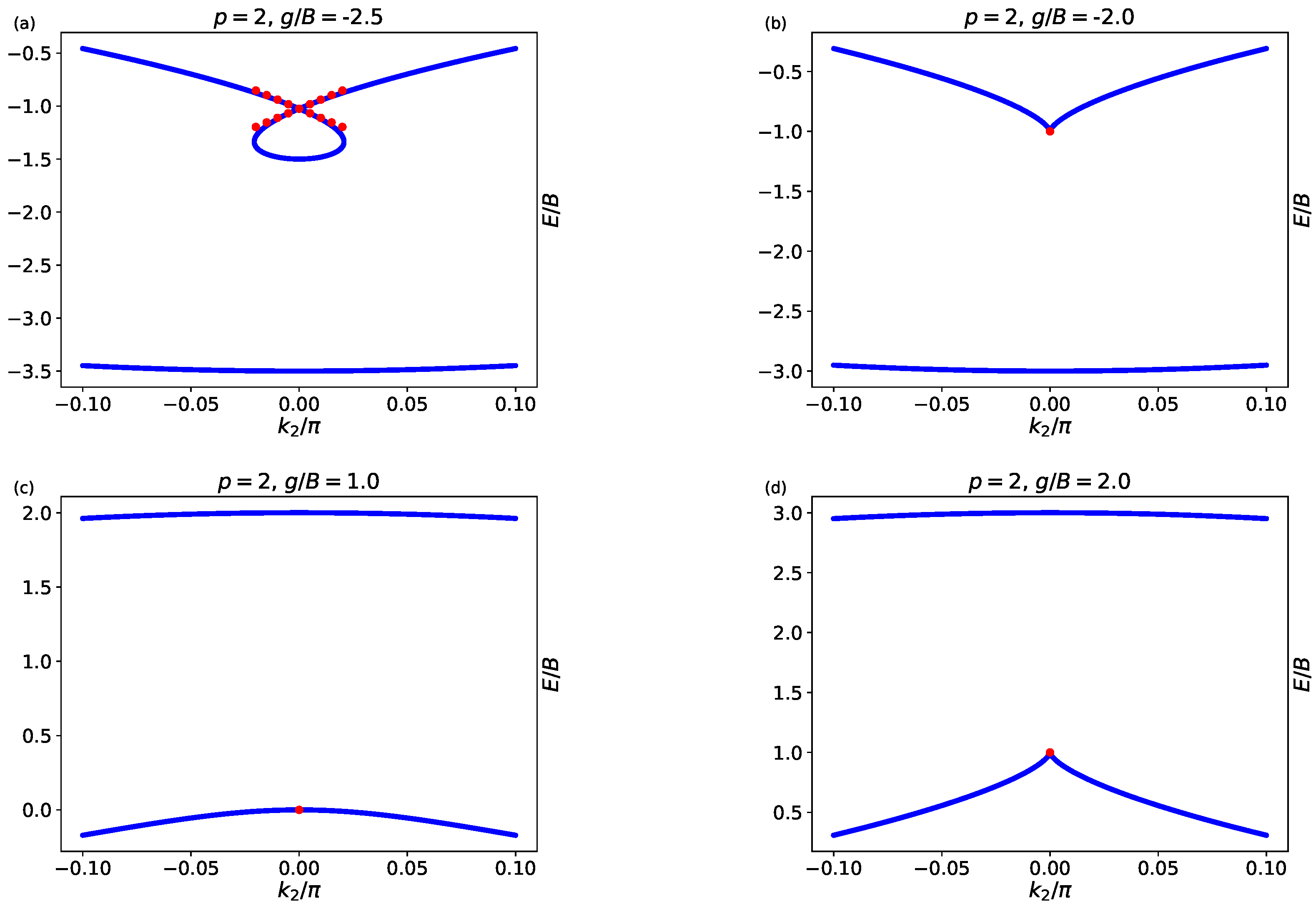
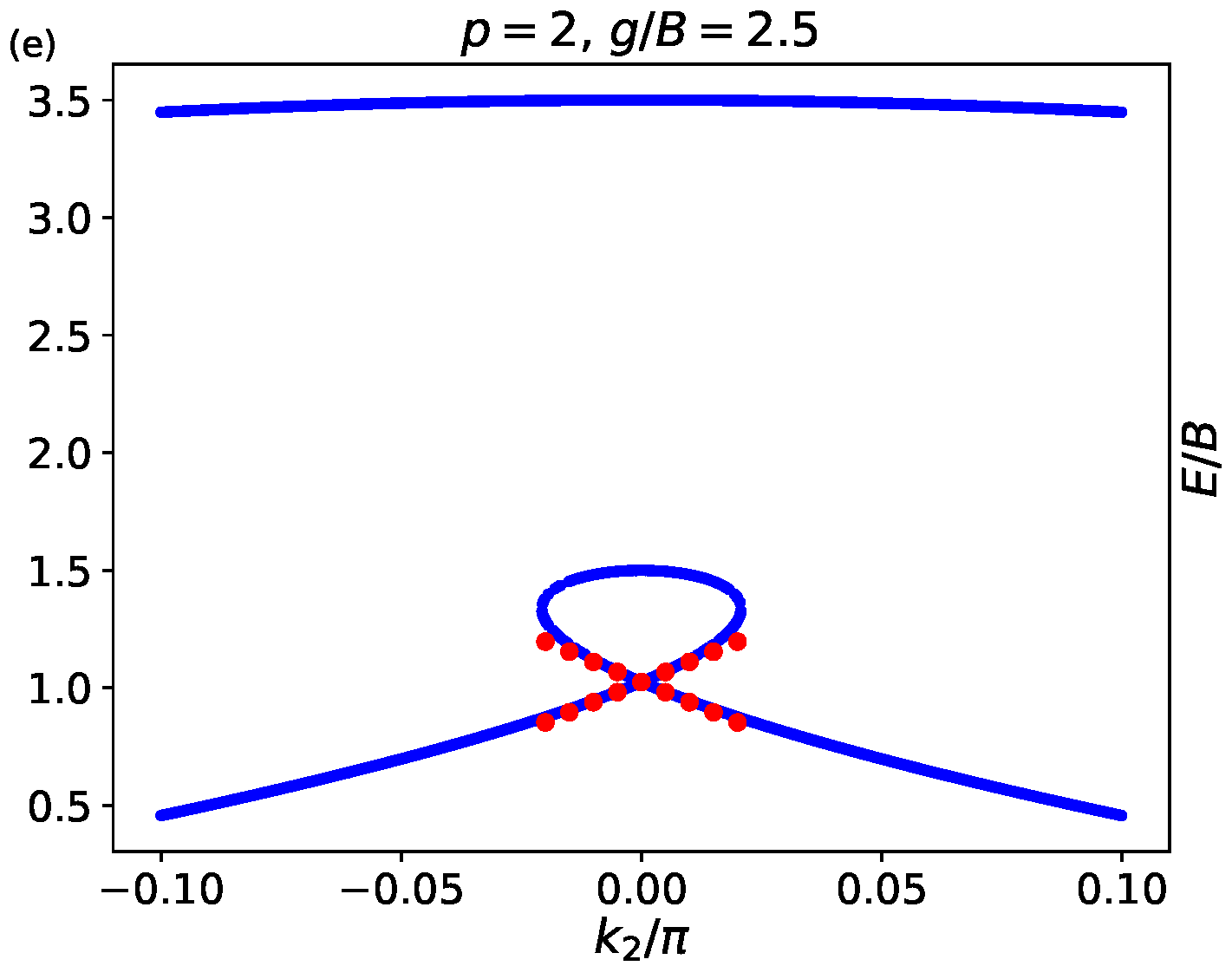
Appendix A.2. Dynamics around the Dirac Cone
References
- Bomantara, R.; Zhao, W.; Zhou, L.; Gong, J. Nonlinear Dirac cones. Phys. Rev. B 2017, 96, 121406. [Google Scholar] [CrossRef] [Green Version]
- New, G. Introduction to Nonlinear Optics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Tuloup, T.; Bomantara, R.; Lee, C.; Gong, J. Nonlinearity induced topological physics in momentum space and real space. Phys. Rev. B 2020, 102, 115411. [Google Scholar] [CrossRef]
- Wu, B.; Niu, Q. Nonlinear Landau-Zener tunneling. Phys. Rev. A 2000, 61, 023402. [Google Scholar] [CrossRef]
- Liu, J.; Fu, L.; Ou, B.; Chen, S.; Choi, D.; Wu, B.; Niu, Q. Theory of nonlinear Landau-Zener tunneling. Phys. Rev. A 2002, 66, 023404. [Google Scholar] [CrossRef] [Green Version]
- Witthaut, D.; Graefe, E.; Korsch, H. Towards a generalized Landau-Zener formula for an interacting Bose-Einstein condensate in a two-level system. Phys. Rev. A 2006, 73, 063609. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Hänggi, P.; Gong, J. Two-mode Bose-Einstein condensate in a high-frequency driving field that directly couples the two modes. Phys. Rev. A 2008, 77, 053607. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Hänggi, P.; Gong, J. Nonlinear Landau–Zener processes in a periodic driving field. New J. Phys. 2008, 10, 073008. [Google Scholar] [CrossRef]
- Qi, X.; Wu, Y.; Zhang, S. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 2006, 74, 085308. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.; Geim, A.; Morozov, S.; Jiang, D.; Katsnelson, M.; Grigorieva, I.; Dubonos, S.; Firsov, A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tan, Y.; Stormer, H.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Ando, T.; Nakanishi, T.; Saito, R. Berry’s Phase and Absence of Back Scattering in Carbon Nanotubes. J. Phys. Soc. Jpn. 1998, 67, 2857–2862. [Google Scholar] [CrossRef] [Green Version]
- Mikitik, G.; Sharlai, Y. Manifestation of Berry’s Phase in Metal Physics. Phys. Rev. Lett. 1999, 82, 2147–2150. [Google Scholar] [CrossRef]
- Tuloup, T.; Bomantara, R.; Gong, J. Topological characteristics of gap closing points in nonlinear Weyl semimetals. Phys. Rev. B 2022, 106, 195411. [Google Scholar] [CrossRef]
- Milovanov, A.; Rasmussen, J.; Dif-Pradalier, G. Self-consistent model of the plasma staircase and nonlinear Schrödinger equation with subquadratic power nonlinearity. Phys. Rev. E 2021, 103, 052218. [Google Scholar] [CrossRef] [PubMed]
- Wazwaz, A. Exact solutions for the fourth order nonlinear Schrodinger equations with cubic and power law nonlinearities. Math. Comput. Model. 2006, 43, 802–808. [Google Scholar] [CrossRef]
- Kilic, B.; Inc, M. Optical solitons for the Schrödinger–Hirota equation with power law nonlinearity by the Bäcklund transformation. Optik 2017, 138, 64–67. [Google Scholar] [CrossRef]
- Sulem, C.; Sulem, P. The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Osman, M.; Lu, D.; Khater, M. A study of optical wave propagation in the nonautonomous Schrödinger-Hirota equation with power-law nonlinearity. Results Phys. 2019, 13, 102157. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Ekici, M.; Zhou, Q.; Biswas, A. Exact solitons to generalized resonant dispersive nonlinear Schrödinger’s equation with power law nonlinearity. Optik 2017, 130, 178–183. [Google Scholar] [CrossRef]
- Dai, C.; Zhang, X.; Fan, Y.; Chen, L. Localized modes of the (n + 1)-dimensional Schrödinger equation with power-law nonlinearities in PT-symmetric potentials. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 239–250. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Vajargah, B.; Biswas, A. Optical solitons and optical rogons of generalized resonant dispersive nonlinear Schrödinger’s equation with power law nonlinearity. Optik 2014, 125, 4246–4256. [Google Scholar] [CrossRef]
- Biswas, A.; Konar, S. Introduction to Non-Kerr Law Optical Solitons; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, Q.-H.; Gong, J. On the Quantization of AB Phase in Nonlinear Systems. Entropy 2022, 24, 1835. https://doi.org/10.3390/e24121835
Liu X, Wang Q-H, Gong J. On the Quantization of AB Phase in Nonlinear Systems. Entropy. 2022; 24(12):1835. https://doi.org/10.3390/e24121835
Chicago/Turabian StyleLiu, Xi, Qing-Hai Wang, and Jiangbin Gong. 2022. "On the Quantization of AB Phase in Nonlinear Systems" Entropy 24, no. 12: 1835. https://doi.org/10.3390/e24121835
APA StyleLiu, X., Wang, Q.-H., & Gong, J. (2022). On the Quantization of AB Phase in Nonlinear Systems. Entropy, 24(12), 1835. https://doi.org/10.3390/e24121835






