Canonical Density Matrices from Eigenstates of Mixed Systems §
Abstract
1. Introduction
2. The Fermi–Hubbard Model with Impurity
3. Measures of Quantum Chaos
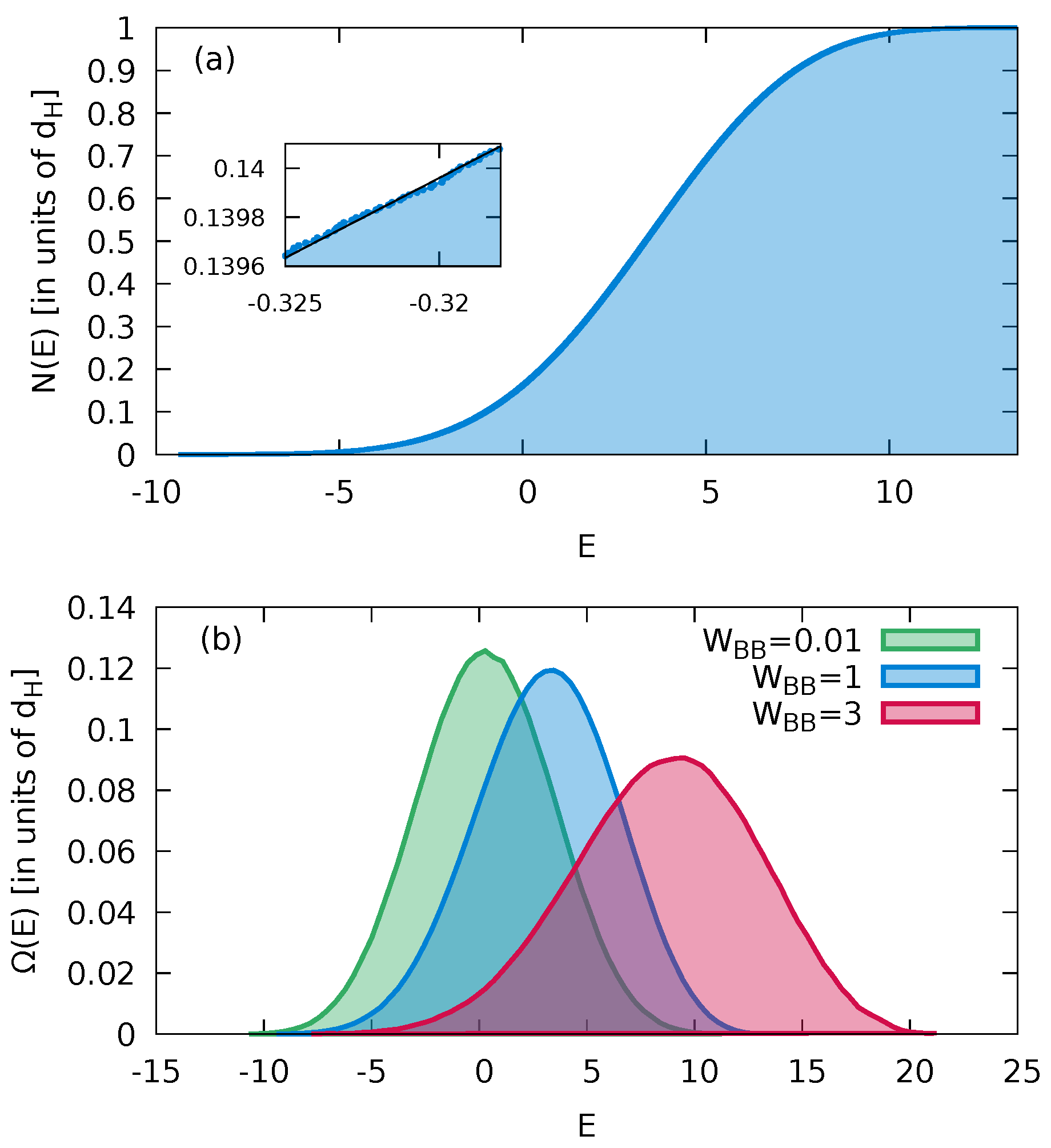
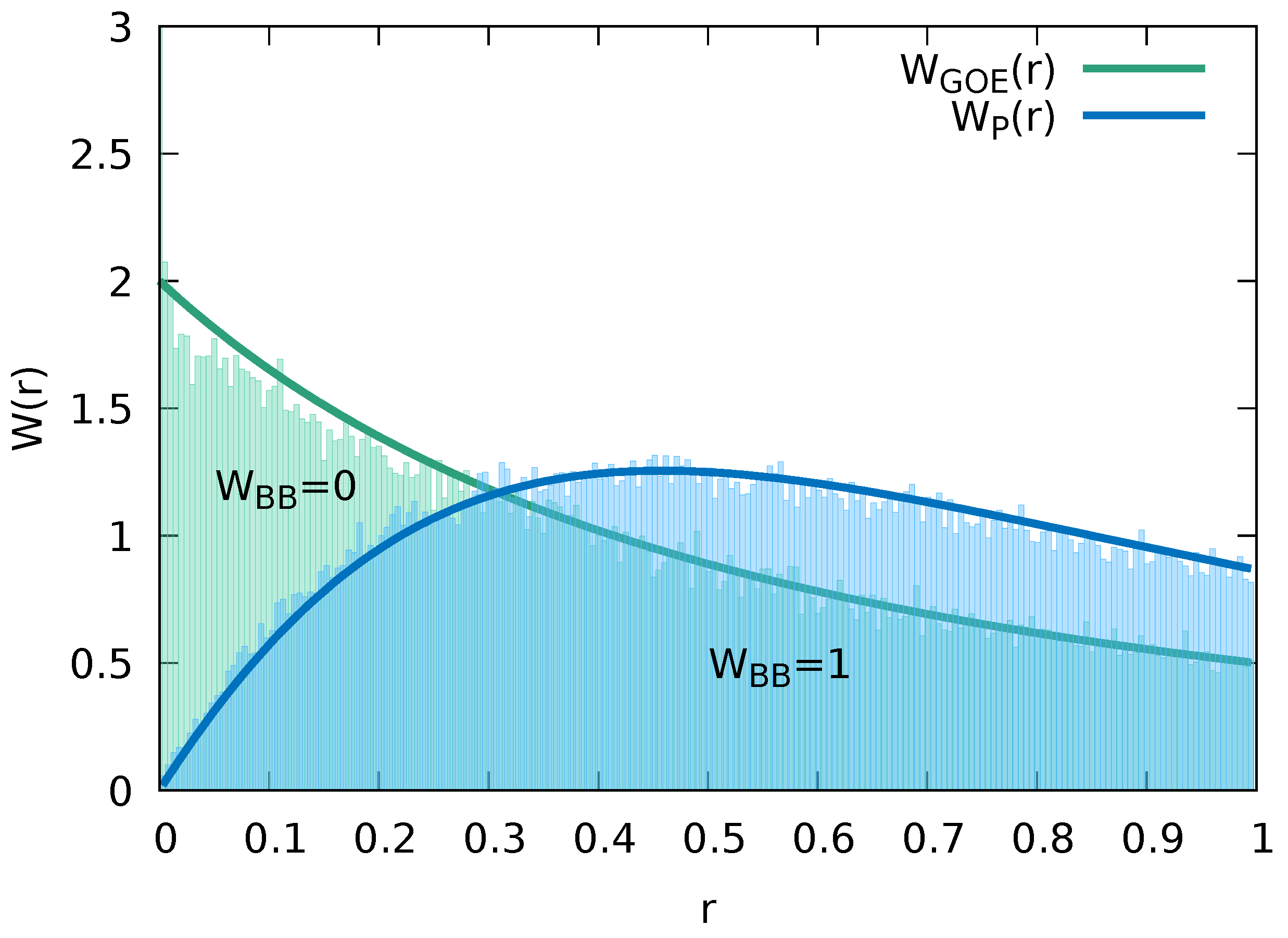
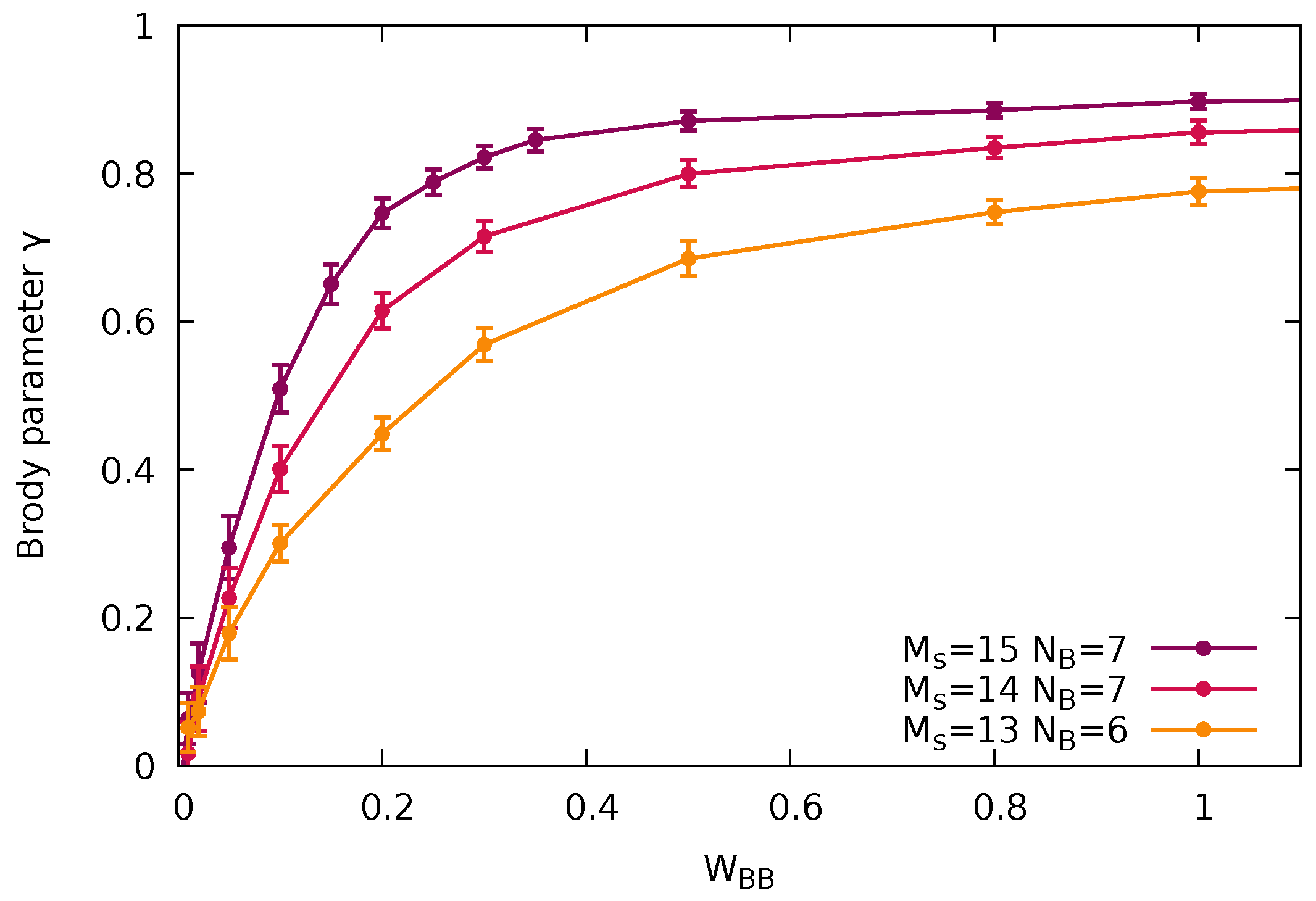
3.1. Spectral Measures
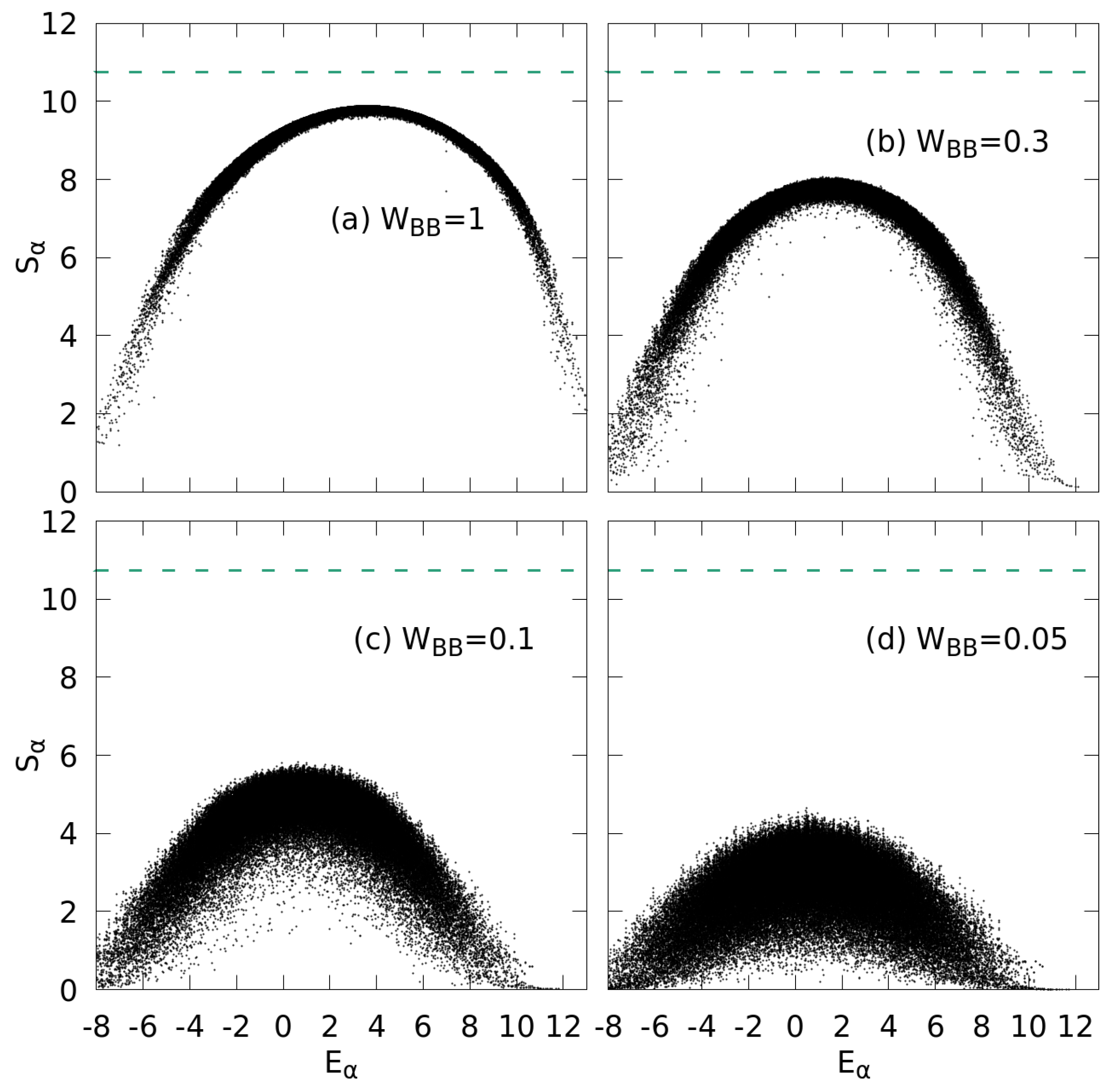
3.2. Measures for Wavefunctions
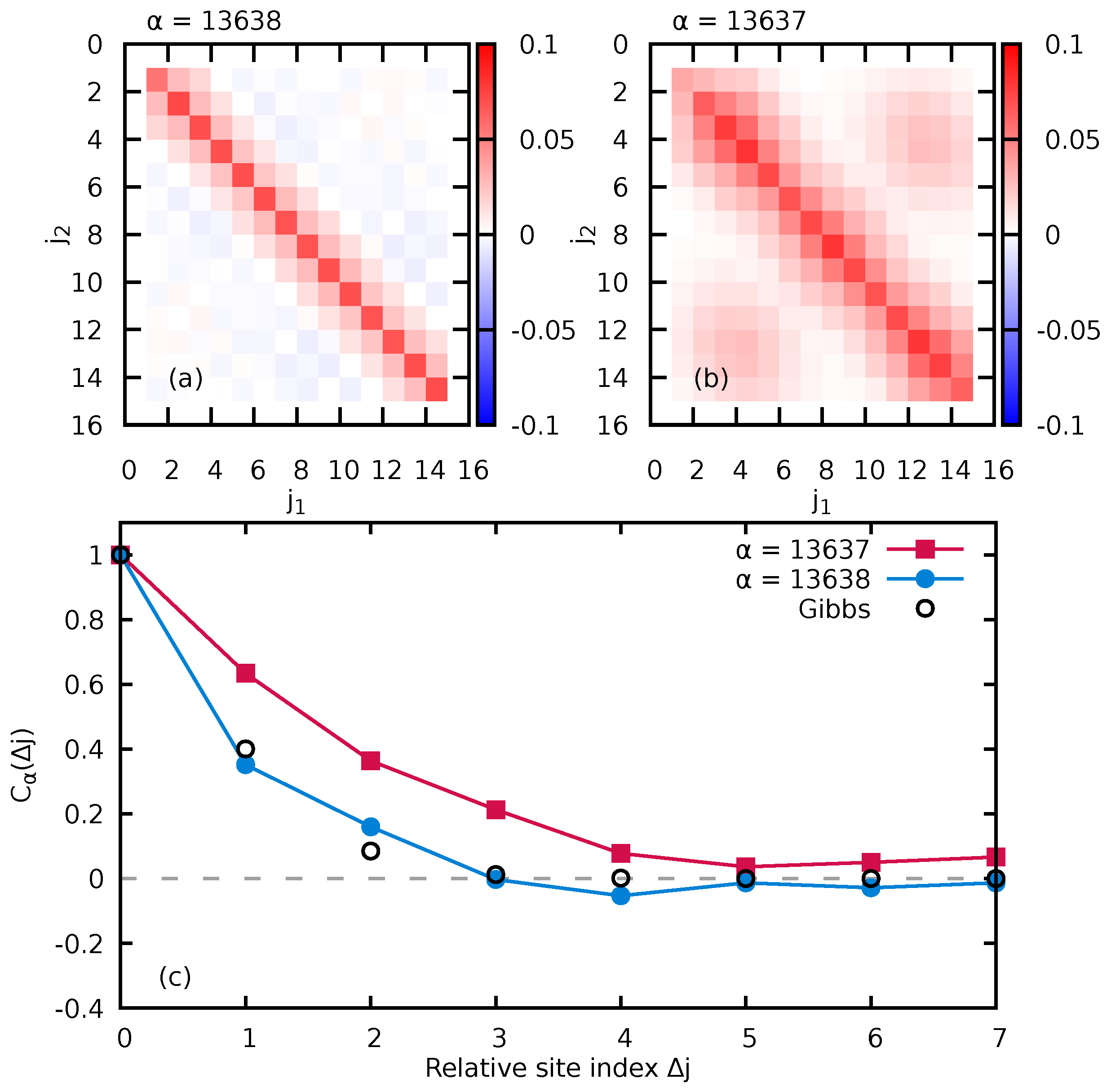
4. The Reduced Density Matrix of the Impurity
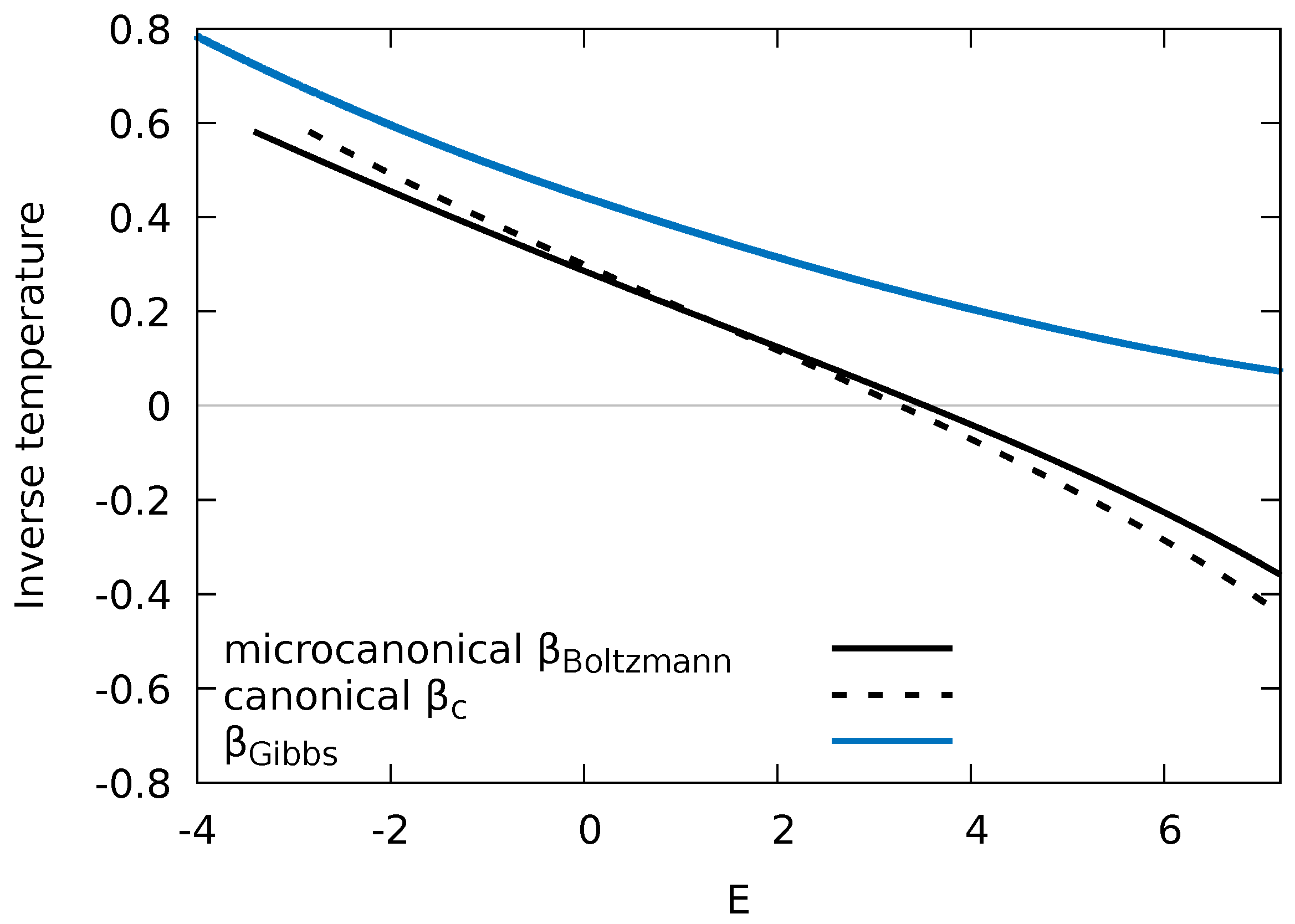
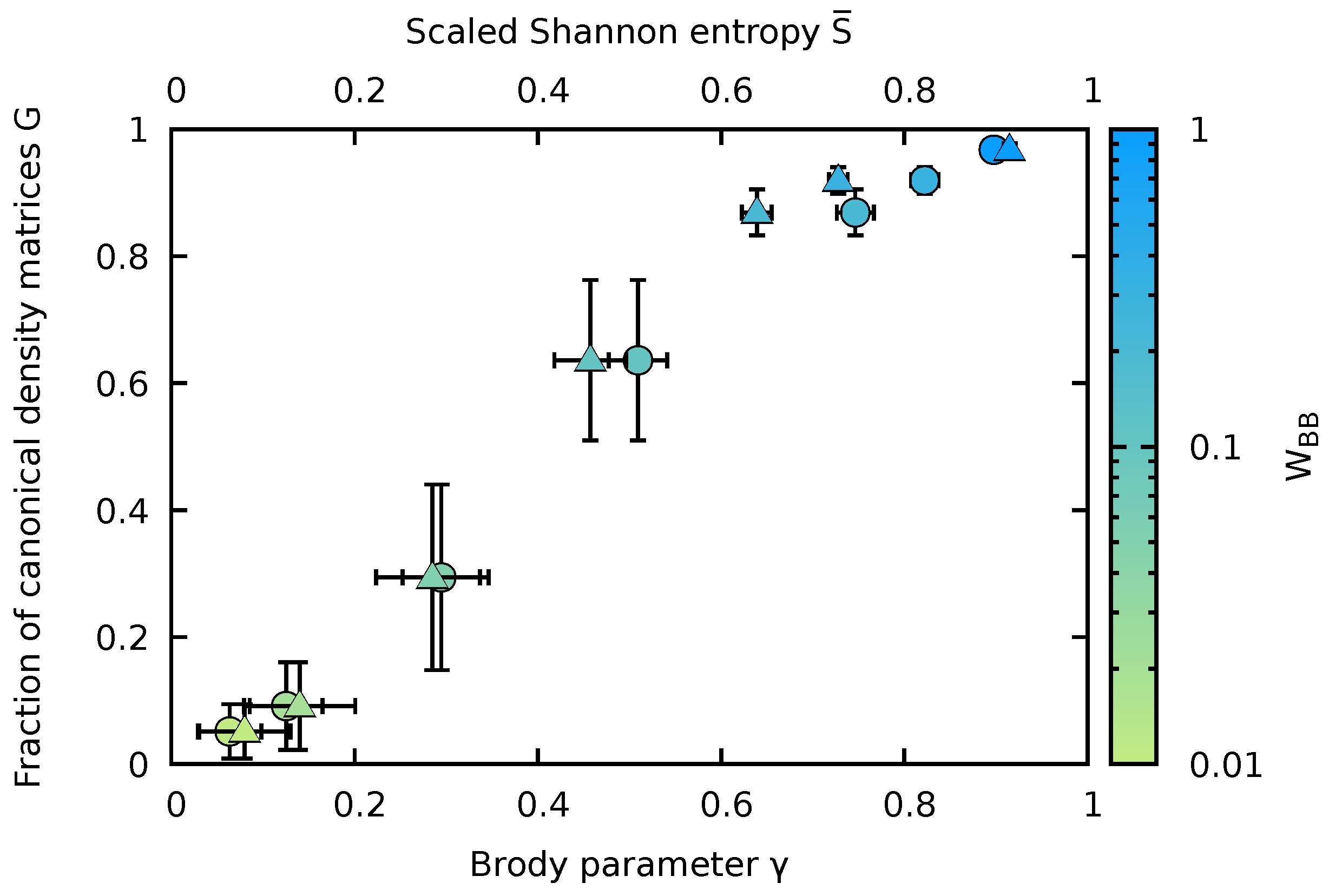
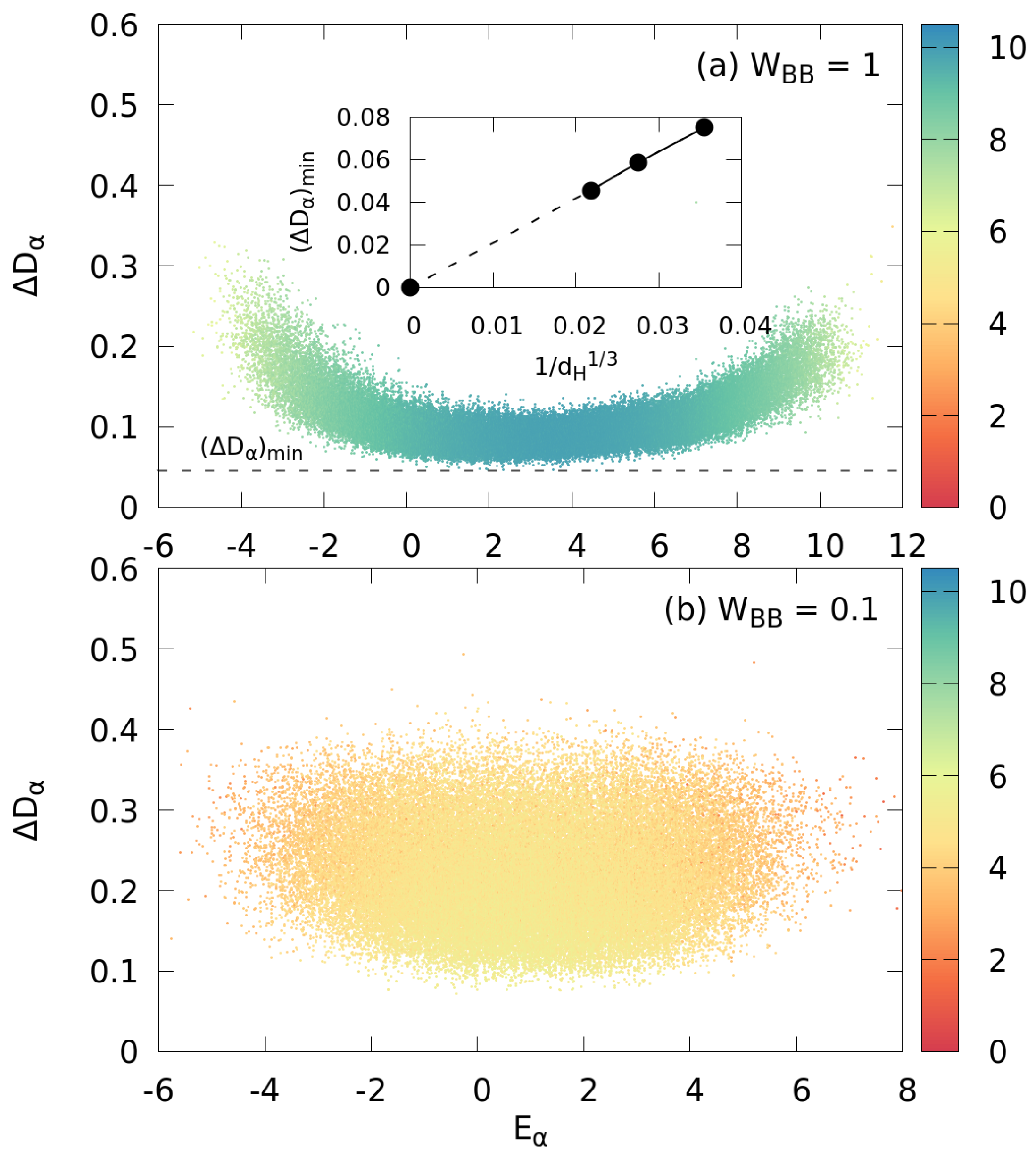
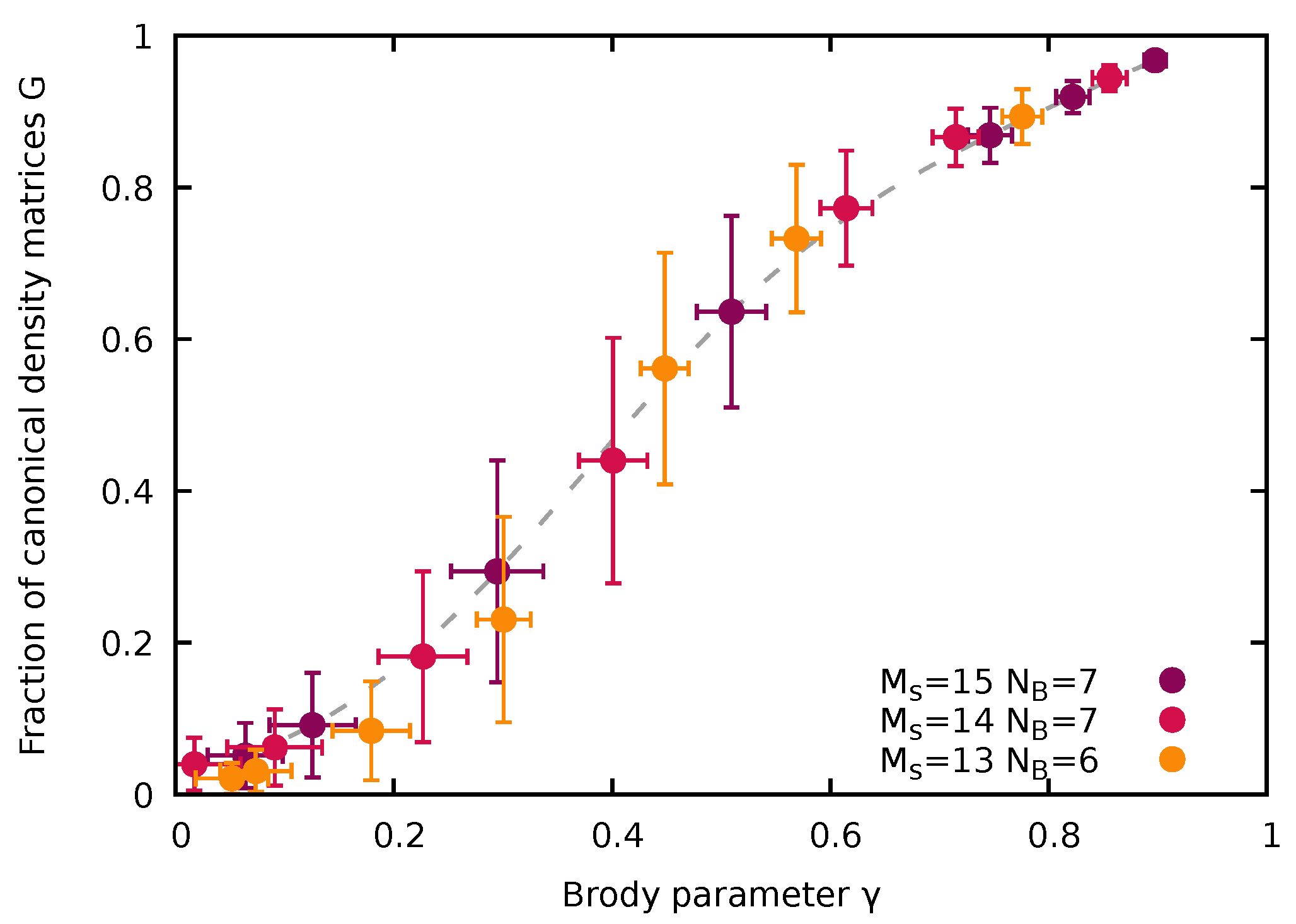
5. Eigenstate Canonicity and Degree of Quantum Chaoticity
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOS | Density of states |
| ETH | Eigenstate thermalization hypothesis |
| GOE | Gaussian orthogonal ensemble |
| MF | Mean field |
| NNLS | Nearest-neighbor level spacing |
| RDM | Reduced density matrix |
References
- Boltzmann, L. Vorlesungen über Gastheorie; Verlag Johann Ambrosius Barth: Leipzig, Germany, 1896. [Google Scholar]
- Huang, K. Statistical Mechanics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1979. [Google Scholar]
- Lichtenberg, A.J.; Lieberman, M.A. Regular and Chaotic Dynamics; Springer: New York, NY, USA, 1991. [Google Scholar]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Thermal fluctuations in quantized chaotic systems. J. Phys. A Math. Gen. 1996, 29, L75–L79. [Google Scholar] [CrossRef]
- Srednicki, M. The approach to thermal equilibrium in quantized chaotic systems. J. Phys. A Math. Gen. 1999, 32, 1163–1175. [Google Scholar] [CrossRef]
- Zelevinsky, V.; Brown, B.A.; Frazier, N.; Horoi, M. The nuclear shell model as a testing ground for many-body quantum chaos. Phys. Rep. 1996, 276, 85–176. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M.; Casati, G. Towards a statistical theory of finite Fermi systems and compound states: Random two-body interaction approach. Phys. Rev. E 1996, 54, 2136–2139. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M. Statistical theory of finite Fermi systems based on the structure of chaotic eigenstates. Phys. Rev. E 1997, 56, 5144–5159. [Google Scholar] [CrossRef]
- Borgonovi, F.; Guarneri, I.; Izrailev, F.; Casati, G. Chaos and thermalization in a dynamical model of two interacting particles. Phys. Lett. A 1998, 247, 140–144. [Google Scholar] [CrossRef]
- Borgonovi, F.; Celardo, G.; Izrailev, F.M.; Casati, G. Semiquantal Approach to Finite Systems of Interacting Particles. Phys. Rev. Lett. 2002, 88, 054101. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.; Santos, L.; Zelevinsky, V. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef]
- Müller, M.P.; Adlam, E.; Masanes, L.; Wiebe, N. Thermalization and Canonical Typicality in Translation-Invariant Quantum Lattice Systems. Commun. Math. Phys. 2015, 340, 499–561. [Google Scholar] [CrossRef]
- Reimann, P.; Gemmer, J. Why are macroscopic experiments reproducible? Imitating the behavior of an ensemble by single pure states. Phys. A Stat. Mech. Its Appl. 2020, 552, 121840. [Google Scholar] [CrossRef]
- Brenes, M.; Pappalardi, S.; Goold, J.; Silva, A. Multipartite Entanglement Structure in the Eigenstate Thermalization Hypothesis. Phys. Rev. Lett. 2020, 124, 040605. [Google Scholar] [CrossRef] [PubMed]
- Brenes, M.; Pappalardi, S.; Mitchison, M.T.; Goold, J.; Silva, A. Out-of-time-order correlations and the fine structure of eigenstate thermalization. Phys. Rev. E 2021, 104, 034120. [Google Scholar] [CrossRef] [PubMed]
- Sugimoto, S.; Hamazaki, R.; Ueda, M. Eigenstate Thermalization in Long-Range Interacting Systems. Phys. Rev. Lett. 2022, 129, 030602. [Google Scholar] [CrossRef]
- Wang, J.; Benenti, G.; Casati, G.; Wang, W.G. Complexity of quantum motion and quantum-classical correspondence: A phase-space approach. Phys. Rev. Res. 2020, 2, 043178. [Google Scholar] [CrossRef]
- Wang, J.; Benenti, G.; Casati, G.; Wang, W.g. Quantum chaos and the correspondence principle. Phys. Rev. E 2021, 103, L030201. [Google Scholar] [CrossRef]
- Braun, S.; Ronzheimer, J.P.; Schreiber, M.; Hodgman, S.S.; Rom, T.; Bloch, I.; Schneider, U. Negative Absolute Temperature for Motional Degrees of Freedom. Science 2013, 339, 52–55. [Google Scholar] [CrossRef]
- Kaufman, A.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Schittko, R.; Preiss, P.M.; Greiner, M. Quantum thermalization through entanglement in an isolated many-body system. Science 2016, 353, 794–800. [Google Scholar] [CrossRef]
- Jansen, D.; Stolpp, J.; Vidmar, L.; Heidrich-Meisner, F. Eigenstate thermalization and quantum chaos in the Holstein polaron model. Phys. Rev. B 2019, 99, 155130. [Google Scholar] [CrossRef]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Prüfer, M.; Kunkel, P.; Strobel, H.; Lannig, S.; Linnemann, D.; Schmied, C.M.; Berges, J.; Gasenzer, T.; Oberthaler, M.K. Observation of universal dynamics in a spinor Bose gas far from equilibrium. Nature 2018, 563, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Erne, S.; Bücker, R.; Gasenzer, T.; Berges, J.; Schmiedmayer, J. Universal dynamics in an isolated one-dimensional Bose gas far from equilibrium. Nature 2018, 563, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Scherg, S.; Kohlert, T.; Sala, P.; Pollmann, F.; Hebbe Madhusudhana, B.; Bloch, I.; Aidelsburger, M. Observing non-ergodicity due to kinetic constraints in tilted Fermi-Hubbard chains. Nat. Commun. 2021, 12, 4490. [Google Scholar] [CrossRef]
- Neyenhuis, B.; Zhang, J.; Hess, P.W.; Smith, J.; Lee, A.C.; Richerme, P.; Gong, Z.X.; Gorshkov, A.V.; Monroe, C. Observation of prethermalization in long-range interacting spin chains. Sci. Adv. 2017, 3, e1700672. [Google Scholar] [CrossRef]
- Neill, C.; Roushan, P.; Fang, M.; Chen, Y.; Kolodrubetz, M.; Chen, Z.; Megrant, A.; Barends, R.; Campbell, B.; Chiaro, B.; et al. Ergodic dynamics and thermalization in an isolated quantum system. Nat. Phys. 2016, 12, 1037–1041. [Google Scholar] [CrossRef]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwöck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325–330. [Google Scholar] [CrossRef]
- Neumann, J.V. Beweis des Ergodensatzes und desH-Theorems in der neuen Mechanik. Z. Phys. 1929, 57, 30–70. [Google Scholar] [CrossRef]
- Goldstein, S.; Lebowitz, J.L.; Tumulka, R.; Zanghì, N. Long-time behavior of macroscopic quantum systems: Commentary accompanying the English translation of John von Neumann’s 1929 article on the quantum ergodic theorem. Eur. Phys. J. H 2010, 35, 173–200. [Google Scholar] [CrossRef]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Siskens, T.J.; Bongaarts, P.J.M. Ergodicity of operators in finite quantum systems. Physica 1973, 68, 315–341. [Google Scholar] [CrossRef]
- Bongaarts, P.J.M.; Siskens, T.J. Observables, constants of the motion and ergodicity in quantum-statistical mechanics of finite systems. Physica 1974, 71, 529–559. [Google Scholar] [CrossRef]
- Mori, T.; Ikeda, T.N.; Kaminishi, E.; Ueda, M. Thermalization and prethermalization in isolated quantum systems: A theoretical overview. J. Phys. At. Mol. Opt. Phys. 2018, 51, 112001. [Google Scholar] [CrossRef]
- Popescu, S.; Short, A.J.; Winter, A. Entanglement and the foundations of statistical mechanics. Nat. Phys. 2006, 2, 754–758. [Google Scholar] [CrossRef]
- Goldstein, S.; Lebowitz, J.L.; Tumulka, R.; Zanghì, N. Canonical Typicality. Phys. Rev. Lett. 2006, 96, 050403. [Google Scholar] [CrossRef] [PubMed]
- Reimann, P. Typicality for Generalized Microcanonical Ensembles. Phys. Rev. Lett. 2007, 99, 160404. [Google Scholar] [CrossRef]
- Schrödinger, E. Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon Press: Oxford, UK, 1958. [Google Scholar]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws. Phys. Rev. Lett. 1984, 52, 1–4. [Google Scholar] [CrossRef]
- Casati, G.; Chirikov, B.V.; Izraelev, F.M.; Ford, J. Stochastic behavior of a quantum pendulum under a periodic perturbation. In Stochastic Behavior in Classical and Quantum Hamiltonian Systems; Series Title: Lecture Notes in Physics; Casati, G., Ford, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1979; Volume 93, pp. 334–352. [Google Scholar] [CrossRef]
- Casati, G. Relevance of classical chaos in quantum mechanics: The hydrogen atom in a monochromatic field. Phys. Rep. 1987, 154, 77–123. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Gutzwiller, M. Chaos in Classical and Quantum Mechanics; Springer: New York, NY, USA, 1990. [Google Scholar]
- Berry, M. Quantum chaology, not quantum chaos. Phys. Scr. 1989, 40, 335–336. [Google Scholar] [CrossRef]
- Prosen, T.; Robnik, M. Energy level statistics in the transition region between integrability and chaos. J. Phys. A Math. Gen. 1993, 26, 2371–2387. [Google Scholar] [CrossRef]
- Berry, M.V.; Tabor, M. Level Clustering in the Regular Spectrum. Proc. R. Soc. A Math. Phys. Eng. Sci. 1977, 356, 375–394. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Elsevier Academic Press: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Shapiro, M.; Goelman, G. Onset of Chaos in an Isolated Energy Eigenstate. Phys. Rev. Lett. 1984, 53, 1714–1717. [Google Scholar] [CrossRef]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef] [PubMed]
- Rigol, M. Breakdown of Thermalization in Finite One-Dimensional Systems. Phys. Rev. Lett. 2009, 103, 100403. [Google Scholar] [CrossRef]
- Rigol, M. Quantum quenches and thermalization in one-dimensional fermionic systems. Phys. Rev. A 2009, 80, 053607. [Google Scholar] [CrossRef]
- Rigol, M.; Srednicki, M. Alternatives to Eigenstate Thermalization. Phys. Rev. Lett. 2012, 108, 110601. [Google Scholar] [CrossRef]
- Santos, L.F.; Rigol, M. Localization and the effects of symmetries in the thermalization properties of one-dimensional quantum systems. Phys. Rev. E 2010, 82, 031130. [Google Scholar] [CrossRef]
- Santos, L.F.; Rigol, M. Onset of quantum chaos in one-dimensional bosonic and fermionic systems and its relation to thermalization. Phys. Rev. E 2010, 81, 036206. [Google Scholar] [CrossRef]
- Genway, S.; Ho, A.F.; Lee, D.K.K. Dynamics of Thermalization in Small Hubbard-Model Systems. Phys. Rev. Lett. 2010, 105, 260402. [Google Scholar] [CrossRef]
- Genway, S.; Ho, A.F.; Lee, D.K.K. Thermalization of local observables in small Hubbard lattices. Phys. Rev. A 2012, 86, 023609. [Google Scholar] [CrossRef]
- Kim, H.; Ikeda, T.N.; Huse, D.A. Testing whether all eigenstates obey the eigenstate thermalization hypothesis. Phys. Rev. E 2014, 90, 052105. [Google Scholar] [CrossRef]
- Garrison, J.R.; Grover, T. Does a Single Eigenstate Encode the Full Hamiltonian? Phys. Rev. X 2018, 8, 021026. [Google Scholar] [CrossRef]
- Schlagheck, P.; Shepelyansky, D.L. Dynamical thermalization in Bose-Hubbard systems. Phys. Rev. E 2016, 93, 012126. [Google Scholar] [CrossRef]
- Brenes, M.; LeBlond, T.; Goold, J.; Rigol, M. Eigenstate Thermalization in a Locally Perturbed Integrable System. Phys. Rev. Lett. 2020, 125, 070605. [Google Scholar] [CrossRef]
- Santos, L.F.; Polkovnikov, A.; Rigol, M. Weak and strong typicality in quantum systems. Phys. Rev. E 2012, 86, 010102. [Google Scholar] [CrossRef] [PubMed]
- Krause, U.; Pellegrin, T.; Brouwer, P.W.; Abanin, D.A.; Filippone, M. Nucleation of Ergodicity by a Single Mobile Impurity in Supercooled Insulators. Phys. Rev. Lett. 2021, 126, 030603. [Google Scholar] [CrossRef]
- Gaunt, A.L.; Schmidutz, T.F.; Gotlibovych, I.; Smith, R.P.; Hadzibabic, Z. Bose-Einstein Condensation of Atoms in a Uniform Potential. Phys. Rev. Lett. 2013, 110, 200406. [Google Scholar] [CrossRef] [PubMed]
- Fukuhara, T.; Kantian, A.; Endres, M.; Cheneau, M.; Schauß, P.; Hild, S.; Bellem, D.; Schollwöck, U.; Giamarchi, T.; Gross, C.; et al. Quantum dynamics of a mobile spin impurity. Nat. Phys. 2013, 9, 235–241. [Google Scholar] [CrossRef]
- Haller, E.; Hudson, J.; Kelly, A.; Cotta, D.A.; Peaudecerf, B.; Bruce, G.D.; Kuhr, S. Single-atom imaging of fermions in a quantum-gas microscope. Nat. Phys. 2015, 11, 738–742. [Google Scholar] [CrossRef]
- Parsons, M.F.; Huber, F.; Mazurenko, A.; Chiu, C.S.; Setiawan, W.; Wooley-Brown, K.; Blatt, S.; Greiner, M. Site-Resolved Imaging of Fermionic Li 6 in an Optical Lattice. Phys. Rev. Lett. 2015, 114, 213002. [Google Scholar] [CrossRef]
- Cheuk, L.W.; Nichols, M.A.; Okan, M.; Gersdorf, T.; Ramasesh, V.V.; Bakr, W.S.; Lompe, T.; Zwierlein, M.W. Quantum-Gas Microscope for Fermionic Atoms. Phys. Rev. Lett. 2015, 114, 193001. [Google Scholar] [CrossRef] [PubMed]
- Greif, D.; Parsons, M.F.; Mazurenko, A.; Chiu, C.S.; Blatt, S.; Huber, F.; Ji, G.; Greiner, M. Site-resolved imaging of a fermionic Mott insulator. Science 2016, 351, 953–957. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842–845. [Google Scholar] [CrossRef] [PubMed]
- Boll, M.; Hilker, T.A.; Salomon, G.; Omran, A.; Nespolo, J.; Pollet, L.; Bloch, I.; Gross, C. Spin- and density-resolved microscopy of antiferromagnetic correlations in Fermi-Hubbard chains. Science 2016, 353, 1257–1260. [Google Scholar] [CrossRef]
- Berry, M.V. Regular and irregular semiclassical wavefunctions. J. Phys. A Math. Gen. 1977, 10, 2083–2091. [Google Scholar] [CrossRef]
- Pandey, M.; Claeys, P.W.; Campbell, D.K.; Polkovnikov, A.; Sels, D. Adiabatic Eigenstate Deformations as a Sensitive Probe for Quantum Chaos. Phys. Rev. X 2020, 10, 041017. [Google Scholar] [CrossRef]
- Wang, Q.; Robnik, M. Statistical properties of the localization measure of chaotic eigenstates in the Dicke model. Phys. Rev. E 2020, 102, 032212. [Google Scholar] [CrossRef]
- Lozej, C.; Casati, G.; Prosen, T. Quantum chaos in triangular billiards. Phys. Rev. Res. 2022, 4, 013138. [Google Scholar] [CrossRef]
- Li, B.; Robnik, M. Statistical properties of high-lying chaotic eigenstates. J. Phys. A Math. Gen. 1994, 27, 5509–5523. [Google Scholar] [CrossRef]
- Gurevich, I.I.; Pevzner, M.I. “Repulsion” of Nuclear Levels. J. Exp. Theor. Phys. 1957, 4, 278. [Google Scholar]
- Oganesyan, V.; Huse, D.A. Localization of interacting fermions at high temperature. Phys. Rev. B 2007, 75, 155111. [Google Scholar] [CrossRef]
- Atas, Y.Y.; Bogomolny, E.; Giraud, O.; Roux, G. Distribution of the Ratio of Consecutive Level Spacings in Random Matrix Ensembles. Phys. Rev. Lett. 2013, 110, 084101. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V.; Robnik, M. Semiclassical level spacings when regular and chaotic orbits coexist. J. Phys. A Math. Gen. 1984, 17, 2413–2421. [Google Scholar] [CrossRef]
- Hasegawa, H.; Mikeska, H.J.; Frahm, H. Stochastic formulation of energy-level statistics. Phys. Rev. A 1988, 38, 395–399. [Google Scholar] [CrossRef]
- Caurier, E.; Grammaticos, B.; Ramani, A. Level repulsion near integrability: A random matrix analogy. J. Phys. A Math. Gen. 1990, 23, 4903–4909. [Google Scholar] [CrossRef]
- Lenz, G.; Haake, F. Reliability of small matrices for large spectra with nonuniversal fluctuations. Phys. Rev. Lett. 1991, 67, 1–4. [Google Scholar] [CrossRef]
- Izrailev, F.M. Quantum localization and statistics of quasienergy spectrum in a classically chaotic system. Phys. Lett. A 1988, 134, 13–18. [Google Scholar] [CrossRef]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S.M. Random-matrix physics: Spectrum and strength fluctuations. Rev. Mod. Phys. 1981, 53, 385–479. [Google Scholar] [CrossRef]
- Yang, X.; Burgdörfer, J. Molecular-dynamics approach to the statistical properties of energy levels. Phys. Rev. Lett. 1991, 66, 982–985. [Google Scholar] [CrossRef]
- Libisch, F.; Stampfer, C.; Burgdörfer, J. Graphene quantum dots: Beyond a Dirac billiard. Phys. Rev. B 2009, 79, 115423. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- McDonald, S.W.; Kaufman, A.N. Wave chaos in the stadium: Statistical properties of short-wave solutions of the Helmholtz equation. Phys. Rev. A 1988, 37, 3067–3086. [Google Scholar] [CrossRef] [PubMed]
- Bell, R.J.; Dean, P. Atomic vibrations in vitreous silica. Discuss. Faraday Soc. 1970, 50, 55. [Google Scholar] [CrossRef]
- Blümel, R.; Smilansky, U. Suppression of classical stochasticity by quantum-mechanical effects in the dynamics of periodically perturbed surface-state electrons. Phys. Rev. A 1984, 30, 1040–1051. [Google Scholar] [CrossRef]
- Dunkel, J.; Hilbert, S. Consistent thermostatistics forbids negative absolute temperatures. Nat. Phys. 2014, 10, 67–72. [Google Scholar] [CrossRef]
- Hilbert, S.; Hänggi, P.; Dunkel, J. Thermodynamic laws in isolated systems. Phys. Rev. E 2014, 90, 062116. [Google Scholar] [CrossRef]
- Hertz, P. Über die mechanischen Grundlange der Thermodynamik. Ann. Phys. (Leipz.) 1910, 338, 225–274. [Google Scholar] [CrossRef]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Reprint of the 1902 edition; Dover: Mineola, NY, USA, 2014. [Google Scholar]
- Löwdin, P.O.; Shull, H. Natural Orbitals in the Quantum Theory of Two-Electron Systems. Phys. Rev. 1956, 101, 1730–1739. [Google Scholar] [CrossRef]
- Bera, S.; Schomerus, H.; Heidrich-Meisner, F.; Bardarson, J.H. Many-Body Localization Characterized from a One-Particle Perspective. Phys. Rev. Lett. 2015, 115, 046603. [Google Scholar] [CrossRef]
- Bera, S.; Martynec, T.; Schomerus, H.; Heidrich-Meisner, F.; Bardarson, J.H. One-particle density matrix characterization of many-body localization. Ann. Phys. 2017, 529, 1600356. [Google Scholar] [CrossRef]
- Lezama, T.L.M.; Bera, S.; Schomerus, H.; Heidrich-Meisner, F.; Bardarson, J.H. One-particle density matrix occupation spectrum of many-body localized states after a global quench. Phys. Rev. B 2017, 96, 060202. [Google Scholar] [CrossRef]
- Purcell, E.M.; Pound, R.V. A Nuclear Spin System at Negative Temperature. Phys. Rev. 1951, 81, 279–280. [Google Scholar] [CrossRef]
- Ramsey, N.F. Thermodynamics and Statistical Mechanics at Negative Absolute Temperatures. Phys. Rev. 1956, 103, 20–28. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Local quenches with global effects in interacting quantum systems. Phys. Rev. E 2014, 89, 062110. [Google Scholar] [CrossRef] [PubMed]
- Torres-Herrera, E.J.; Kollmar, D.; Santos, L.F. Relaxation and thermalization of isolated many-body quantum systems. Phys. Scr. 2015, T165, 014018. [Google Scholar] [CrossRef]
- Santos, L.F.; Borgonovi, F.; Izrailev, F.M. Onset of chaos and relaxation in isolated systems of interacting spins: Energy shell approach. Phys. Rev. E 2012, 85, 036209. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourehpaz, M.; Donsa, S.; Lackner, F.; Burgdörfer, J.; Březinová, I. Canonical Density Matrices from Eigenstates of Mixed Systems. Entropy 2022, 24, 1740. https://doi.org/10.3390/e24121740
Kourehpaz M, Donsa S, Lackner F, Burgdörfer J, Březinová I. Canonical Density Matrices from Eigenstates of Mixed Systems. Entropy. 2022; 24(12):1740. https://doi.org/10.3390/e24121740
Chicago/Turabian StyleKourehpaz, Mahdi, Stefan Donsa, Fabian Lackner, Joachim Burgdörfer, and Iva Březinová. 2022. "Canonical Density Matrices from Eigenstates of Mixed Systems" Entropy 24, no. 12: 1740. https://doi.org/10.3390/e24121740
APA StyleKourehpaz, M., Donsa, S., Lackner, F., Burgdörfer, J., & Březinová, I. (2022). Canonical Density Matrices from Eigenstates of Mixed Systems. Entropy, 24(12), 1740. https://doi.org/10.3390/e24121740





