Heart Failure Evolution Model Based on Anomalous Diffusion Theory
Abstract
1. Introduction
2. Materials and Methods
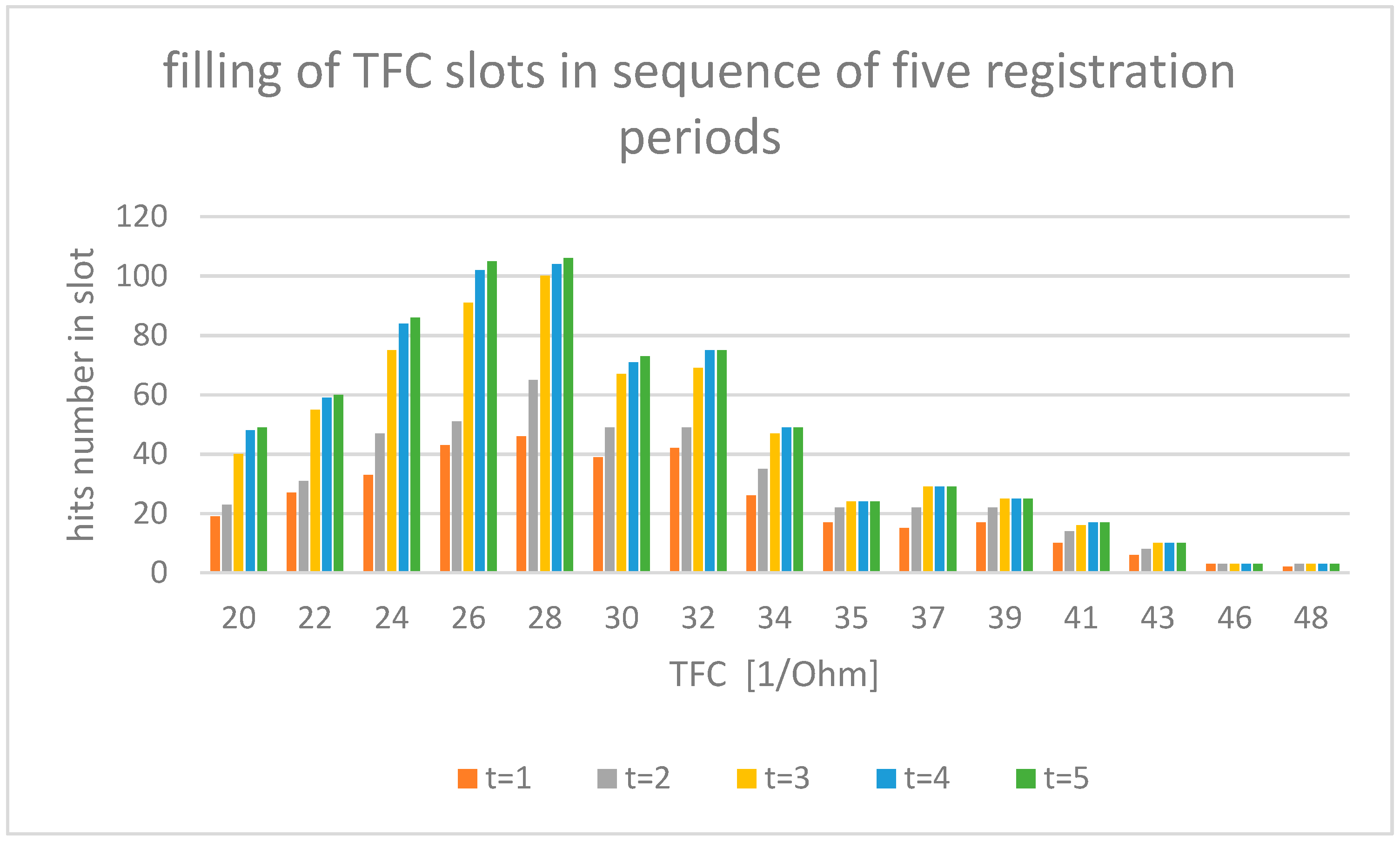
2.1. Experimental Data
2.2. Theoretical Models
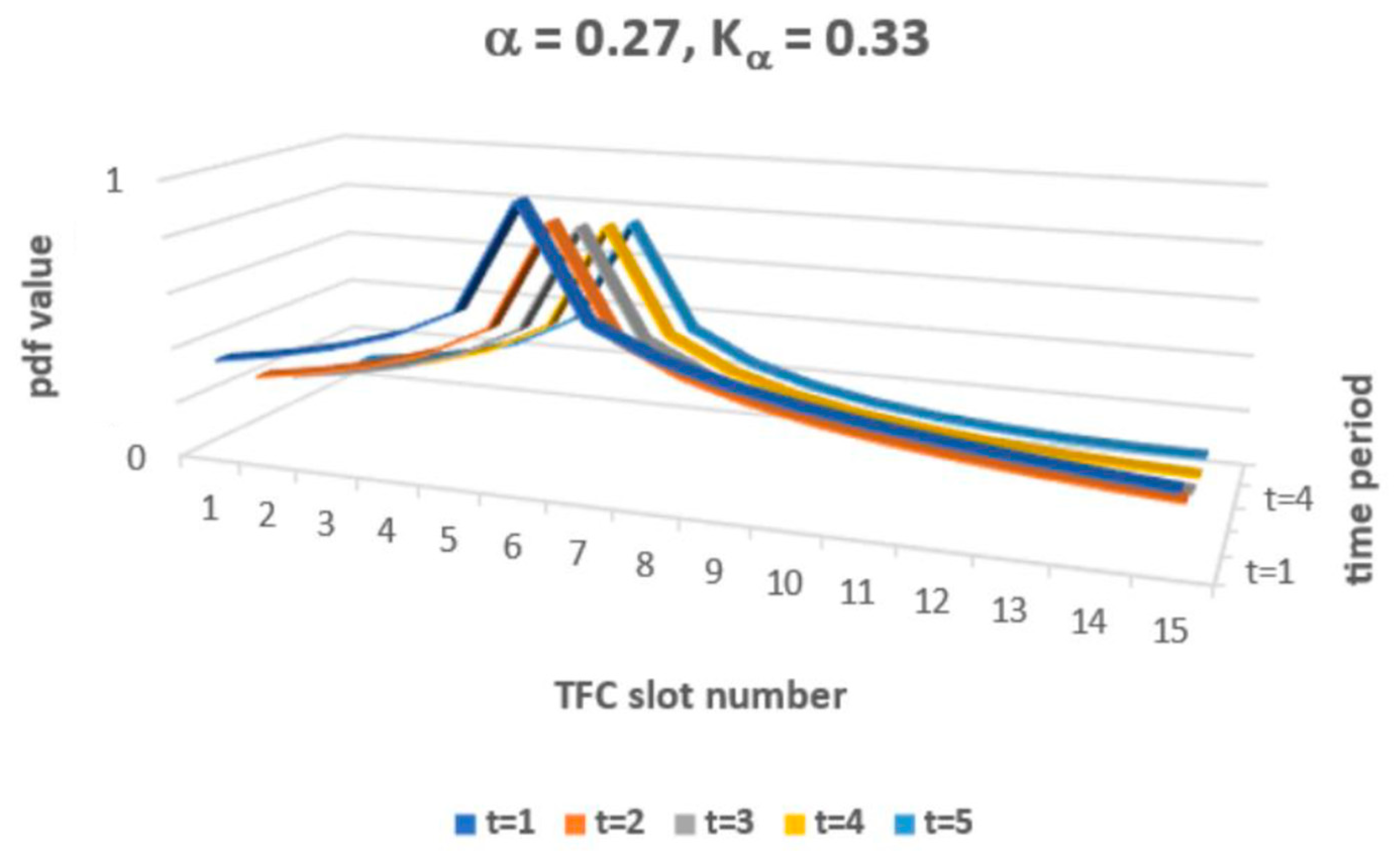
3. Results
4. Discussion
Funding
Conflicts of Interest
References
- Taleb, N.N. The Black Swan—The Impact of the Highly Improbable; Random House: New York, NY, USA, 2007. [Google Scholar]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Wallis, J.R. Noah, Joseph, and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Stanley, H.E.; Mantegna, R.N. An Introduction to Econophysics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- do Valle, I.F.; Roweth, H.G.; Malloy, M.W.; Moco, S.; Barron, D.; Battinelli, E.; Loscalzo, J.; Barabási, A.L. Network medicine framework shows that proximity of polyphenol targets and disease proteins predicts therapeutic effects of polyphenols. Nat. Food 2021, 2, 143–155. [Google Scholar] [CrossRef]
- Moszczynski, P.; Walczak, A.; Krzesinski, P. Prediction of cardiological parameters evolution with the Markov model. In Proceedings of the 37th IBIMA Conference, Cordoba, Spain, 30–31 May 2021. [Google Scholar]
- Walczak, A.; Moszczyński, P.; Krzesiński, P. Evolution of Hemodynamic Parameters Simulated by Means of Diffusion Models. Appl. Sci. 2021, 11, 11412. [Google Scholar] [CrossRef]
- Bassler, K.; Gemunu, E.; Gunaratne, H.; McCauley, J.L. Markov Processes, Hurst Exponents, and Nonlinear Diffusion Equations with application to finance. Phys. A Stat. Mech. Its Appl. 2006, 369, 343–353. [Google Scholar] [CrossRef]
- Krzesinski, P.; Sobotnicki, A.; Gacek, A.; Siebert, J.; Walczak, A.; Murawski, P.; Gielerak, G. Noninvasive Bioimpedance Methods From the Viewpoint of Remote Monitoring in Heart Failure. JMIR mHealth uHealth 2021, 9, e25937. [Google Scholar] [CrossRef] [PubMed]
- Krzesiński, P.; Jankowska, E.A.; Siebert, J.; Galas, A.; Piotrowicz, K.; Stańczyk, A.; Siwołowski, P.; Gutknecht, P.; Chrom, P.; Murawski, P.; et al. Effects of an outpatient intervention comprising nurse-led non-invasive assessments, telemedicine support and remote cardiologists’ decisions in patients with heart failure (AMULET study): A randomised controlled trial. Eur. J. Hear. Fail. 2021, 24, 565–577. [Google Scholar] [CrossRef] [PubMed]
- Krzesiński, P.; Siebert, J.; Jankowska, E.A.; Banasiak, W.; Piotrowicz, K.; Stańczyk, A.; Galas, A.; Walczak, A.; Murawski, P.; Chrom, P.; et al. Rationale and design of the AMULET study: A new Model of telemedical care in patients with heart failure. ESC Hear. Fail. 2021, 8, 2569–2579. [Google Scholar] [CrossRef]
- Krzesiński, P.; Siebert, J.; Jankowska, E.A.; Galas, A.; Piotrowicz, K.; Stańczyk, A.; Siwołowski, P.; Gutknecht, P.; Chrom, P.; Murawski, P.; et al. Nurse-led ambulatory care supported by non-invasive haemodynamic assessment after acute heart failure decompensation. ESC Hear. Fail. 2021, 8, 1018–1026. [Google Scholar] [CrossRef]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; North Holland: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Risken, H. The Fokker Planck Equation; Springer: Berlin, Germany, 1989. [Google Scholar]
- Coley, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation; World Scientific: Singapore, 1996. [Google Scholar]
- Hughes, B.D. Random Walks and Random Environments, Volume 1: Random Walks; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Weiss, G.H. Aspects and Applications of the Random Walk; North-Holland: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Zaslavsky, G.M.; Benkadda, S. Kinetics and Nonlinear Dynamics in Fluids and Plasmas, Chaos; Springer: Berlin, Germany, 1998. [Google Scholar]
- Barabási, A.-L. The origin of bursts and heavy tails in human dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef]
- Oliveira, J.G.; Barabási, A.-L. Darwin and Einstein correspondence patterns. Nature 2005, 437, 1251. [Google Scholar] [CrossRef] [PubMed]
- Dezsö, Z.; Almaas, E.; Lukács, A.; Rácz, B.; Szakadát, I.; Barabási, A.-L. Dynamics of information access on the web. Phys. Rev. E 2006, 73, 066132. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, A. Exact Results for the Barabási Model of Human Dynamics. Phys. Rev. Lett. 2005, 95, 248701. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Barkai, E.; Fleurov, V. Simulating Brownian Type of Motion—The Rescaling Velocity Approach vs Langevin Approach. Phys. Rev. E 1995, 52, 137. [Google Scholar] [CrossRef]
- Barkai, E.; Fleurov, V. Brownian type of motion of a randomly kicked particle far from and close to the diffusion limit. Phys. Rev. E 1995, 52, 1558–1570. [Google Scholar] [CrossRef]
- Barkai, E.; Eisenberg, R.S.; Schuss, Z. Bi-Directional Shot Noise in a Singly Occupied Channel. Phys. Rev. E 1996, 54, 1161. [Google Scholar] [CrossRef]
- Barkai, E.; Fleurov, V. Dissipation and fluctuation for a randomly kicked particle: Normal and anomalous diffusion. Chem. Phys. 1996, 212, 69–88. [Google Scholar] [CrossRef]
- Barkai, E.; Klafter, J. Crossover from Dispersive to Regular Transport in Biased Maps. Phys. Rev. Lett. 1997, 79, 2245–2248. [Google Scholar] [CrossRef]
- Flomenbom, O. Mathematical treatments that solve single molecule. Biophys. Rev. Lett. 2013, 8, 109–136. [Google Scholar] [CrossRef]
- Schlesinger, M.F.; Zaslavsky, G.M.; Klafter, J. Strange Kinetics. Nature 1993, 363, 31–37. [Google Scholar] [CrossRef]
- Hill, R.M.; Dissado, L.A. Debye, and non-Debye relaxation. J. Phys. C Solid State Phys. 1985, 18, 3829–3836. [Google Scholar] [CrossRef]
- Lukichev, A. Relaxation function for the non-Debye relaxation spectra description. Chem. Phys. 2014, 428, 29–33. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P.; Hołyst, J.A. Microscopic explanation of non-Debye relaxation for heat transfer. Phys. A Stat. Mech. Its Appl. 2007, 375, 571–576. [Google Scholar] [CrossRef][Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walczak, A.A. Heart Failure Evolution Model Based on Anomalous Diffusion Theory. Entropy 2022, 24, 1780. https://doi.org/10.3390/e24121780
Walczak AA. Heart Failure Evolution Model Based on Anomalous Diffusion Theory. Entropy. 2022; 24(12):1780. https://doi.org/10.3390/e24121780
Chicago/Turabian StyleWalczak, Andrzej Augustyn. 2022. "Heart Failure Evolution Model Based on Anomalous Diffusion Theory" Entropy 24, no. 12: 1780. https://doi.org/10.3390/e24121780
APA StyleWalczak, A. A. (2022). Heart Failure Evolution Model Based on Anomalous Diffusion Theory. Entropy, 24(12), 1780. https://doi.org/10.3390/e24121780





