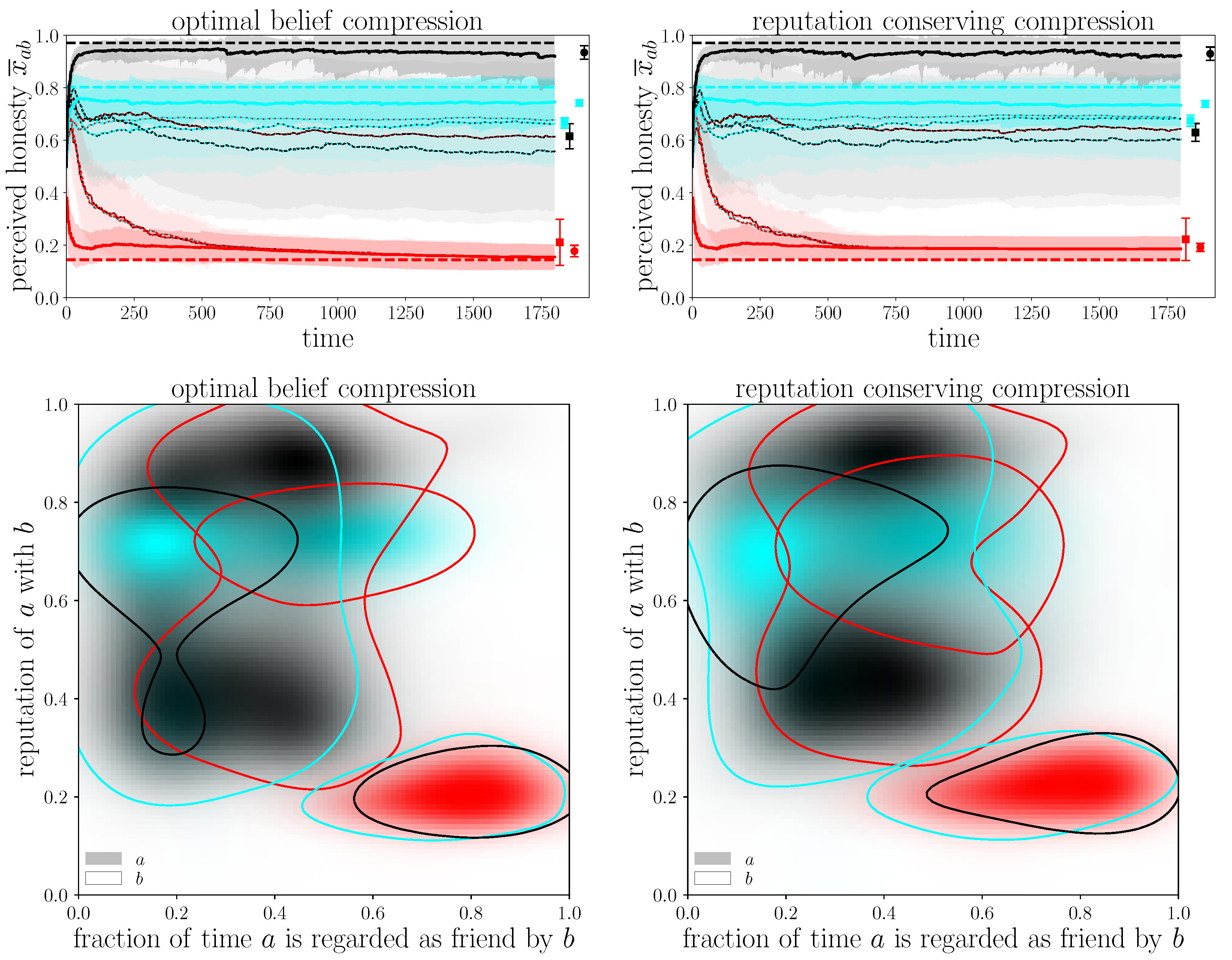
For the following analysis, we use a setup with 50 agents with honesties equally distributed from 0 to 1 and 300 conversation rounds. As shown in [
22], the agents typically form groups in which they have around 3 to 4 other agents with whom they have had at least 100 conversations. These group sizes are comparable to the system sizes used in [
1], where after 100 conversation rounds the simulation was about to reach a steady state. Additionally, we will later see that agents reach quite significant informedness, also suggesting that the presented simulations are sufficiently converged after 300 rounds. Furthermore,
Section 2.5.3 describes the optimal belief compression method used, and the personal character traits of shyness and friendship affinity are distributed randomly and differently in each simulation. For statistical significance, we perform 100 realizations of that simulation with different random seeds.
3.2.1. Honesty and Reputation
First of all, we have a look at the fundamental quantity in the reputation game, the agents’ reputation. Here, reputation is the common view others have on a given agent, i.e., the expectation value of an agent’s honesty under the combined belief states of all others. Since there is no coupling between belief states in the reputation game yet (compare Equation (
2)), we can define the combined opinion of all others about agent
i as
for normalization. With this, we can calculate agent
i’s overall reputation
This definition also ensures that opinions of uninformed agents, i.e., agents that have never (hardly) had any contact with
i, also do not affect agent
i’s reputation, because their
and
are (near) zero and do not (hardly) contribute to all the sums. In
Figure 3 the agents’ reputation is shown in comparison to their real honesties, where perfect reputation assignment would correspond to an identity function. We see that there is a clear tendency for honest agents to be underrated and dishonest agents to be overrated, which in principle was to be expected. Since for a more extreme opinion about someone, much more data is required than to form just a moderate opinion, all belief states naturally tend towards the
. Especially in large system sizes where an agent has a high acquaintance typically to just a few others but by far not all who contribute to that agent’s reputation, most of the time the agents simply had not had enough data to sharpen their opinions. This effect, though, can only explain deviations from an extreme towards a neutral opinion and should only cause a flattening at both ends of the average reputation (black curve). However, we observe many simulations where reputation ended up in just the opposite regime as the actual honesty, and at both ends the average curve even changes direction. On the right we can identify the very honest agents being regarded as strong liars as the reputation game realization of the Cassandra Syndrome. This was already found in the three-agent setup of the reputation game simulation (see [
1]), and can now also be reproduced in the large-scale version. Furthermore, on the left side of
Figure 3 we see a similar, but inverted effect: the strongest liars actually are reputed relatively high, or at least higher than agents with an honesty of around
. This is the case because extreme liars, by almost never saying the truth, hardly reveal any information about themselves at all. Mostly the absence of confessions helps the most extreme liars to maintain a completely fake image of themselves. This way, their reputation decouples from their intrinsic honesty, which leads to the increase of reputation at the very low honesty regime. This fact that very dishonest agents only show a fake image and completely hide their true opinions leads to another important effect, which will be discussed in
Section 3.2.2.
Besides the effects at the very end of the honesty values, there is another non-trivial observation in the middle of
Figure 3. Contrary to expectations, the intersection of the average reputation and the true honesty of an agent is not at
. Rather, the border between being overrated and underrated is at an honesty of about
, meaning that agents generally tend to judge others less honest than they actually are, i.e., are too critical. This leads to the conclusion that for ordinary agents, the Cassandra syndrome and the associated harm are stronger than the positive effect that lies could have when pretending to be honest. This shows that harming others’ reputations by gossiping is relatively easy compared to increasing one’s own reputation with the help of lies. For now, this is also a relevant feature to keep in mind for the remaining analysis of the reputation game dynamics.
3.2.2. Honesty and Informedness
The main goal of the agents is to learn about others’ honesties and to judge them as accurately as possible. Therefore, we introduce an agent’s informedness, which is a measure of how well its worldview is aligned with the ground truth by the end of a simulation. Writing
as an agent
k’s true honesty and
as agent
i’s opinion on
k’s honesty, we can define agent
i’s informedness as
which in the 50-agent setup can be any number between
and
. We can now investigate the correlation of an agent’s informedness with its intrinsic honesty, which is shown in the left panel of
Figure 4. Clearly, we see that both very honest and very dishonest agents are better informed than their medium-honest peers. Let us first analyze why dishonest agents are that well-informed. First of all, for any agent to be well-informed, it is important to gain information by talking to others. Since very honest agents per construction have on average to deal with more dishonest agents and vice versa, dishonest agents on average get more reliable information from conversations with others and are less distorted by lies compared to honest agents. This statement can easily be checked by looking at the correlation between an agent’s informedness and the average honesty of their neighborhood. A neighborhood of an agent
i is hereby defined as the set of all agents that agent
i has at least talked to once in the simulation. To calculate the average honesty of a neighborhood, we weight the individual honesties of neighbors by the number of conversations they had with the central agent, i.e., by the closeness of the two agents. Thus, the average honesty of a neighborhood
of an agent
i is given by
where
is the number of conversations two agents
i and
j have had with each other. Following the statement above, one would intuitively assume that the more honest one’s surrounding agents are, the more true information should circulate in this neighborhood and the better should be the informedness of the agents within that neighborhood. However, when looking at the upper-right panel of
Figure 4, one does not see a clear correlation for particularly honest or dishonest agents or for average agents. Instead, the best informedness values are reached by agents within a medium-honest environment, but this could as well be a coincidence, because there are only a few very well-informed agents, and the probability of them ending up in a medium-honest environment is higher than in an extreme one. Nevertheless, it is interesting to observe that the honesty of an agent’s neighborhood has no large impact on its informedness, suggesting that the lie detection mechanism of the agents works well enough, such that they are not completely dependent on others’ trustworthiness. On the other side, this could mean that agents are not able to profit from very honest environments, as they probably underestimate the honesty of many of their neighbors in such situations, but we will later see that there is another plausible explanation for this. Anyways, since only an honest environment does not make the agents well-informed, we assume the high informedness of dishonest agents has a more fundamental cause. As already discussed in
Section 3.2.1, dishonest agents build up a completely fake image of themselves by hardly revealing any information about themselves at all, which makes it very hard for others to assess their belief states. This in turn would be the basis for others to target their lies towards dishonest agents, because in order to go undetected, agents try to manipulate the receiver’s current estimated opinion when lying (see Equation (
7)). However, since other agents can not estimate the dishonest receiver’s current opinion, they can also only badly adapt the lie, which consequentially is more likely to be detected. This way, strong liars maneuver themself in a very good position for detecting lies, which makes them less prone to others’ manipulations and results in higher informedness values. On the other hand, let us now understand why very honest agents are better informed than others. Again, in
Section 3.2.1 and
Figure 3 we have already seen that honest agents suffer from the Cassandra syndrome quite frequently. This means that often they are not believed although they say the truth, which results in a misjudgment of belief states by their conversation partners. Similar to dishonest agents, this mismatch between honest agents’ belief states and others’ estimations of that leads to easier detectable lies and better informedness.
Let us have a look at this finding from an information trading perspective. Although not implemented in the reputation game yet, information trading is part of humans’ everyday life as one chooses conversation partners, i.e., one’s information sources also consider the expected quality or value of that conversation partner’s statements. To be known as someone whose knowledge is also worth paying for a little bit, e.g., by revealing one’s own valuable knowledge, is not trivial. First of all, one has to be informed in the very first place, which in the reputation game is the case for both very honest and very dishonest agents. Second, however, this must also be recognized by others and even before that, one has to be believed by others. Only if an agent is both well-informed and perceived as honest, i.e., highly reputed it will profit from trading with information. Especially for honest agents, this could be a problem, because they might only be well-informed if regarded as strong liars, as explained before. To prove this argument, the lowest panel of
Figure 4 compares an agent’s reputation within its neighborhood with its informedness. Similarly to Equation (
21), an agent
i’s reputation within its neighborhood
is thus calculated as
Moreover, this reputation is then compared to an agent’s real honesty, leading to negative values representing underestimation of an agent’s honesty and positive values representing overestimation. One can clearly see a trend in this panel, where both stronger over- and underestimation lead to better informedness values. This again supports the previous thesis that the misjudgment of other agents is what improved an agent’s informedness. For honest agents (left side), this means that they will often not be able to trade with information, because nobody will recognize the true value of their statements. For liars on the other hand, the informedness level even raises with overestimation, i.e., their trading options seem promising. So if a dishonest agent decides to communicate honest, trustworthy information, it would have a big impact because it is both believed and very informative. If, however, it communicates dishonestly as most of the time, the statement still has a large impact as it is perceived as very valuable, but in reality is just an easy way to misguide the receiver. Actually, this is again a very important insight by itself, because having a large influence with false information makes the judgment of others even worse, which in turn ensures that the dishonest agent will not lose its position, but remain able to detect lies very well, i.e., stay well-informed compared to others.
Besides this effect, the lower panel in
Figure 4 also reveals a very simple, but still useful, important insight. Although there are some very extreme over- or underestimations of agents in the left and right edges of the panel, the vast majority of points are located near the center. In particular, most points spread in a range between
and
, meaning that the agents got their opinions right, mainly with a deviation of less than
. This means that for most cases a neighborhood of agents is very well able to assign the right reputation to an embedded agent with reasonably good precision. Thus, we can generally conclude that the modeling approach, and especially the lie-detection and updating mechanisms, i.e., the learning mechanisms implemented in the reputation game, work well on a neighborhood-averaged level.
When again looking at the upper left panel of
Figure 4, we obverse a clear asymmetry between dishonest and honest agents. Dishonest ones seem to be even better informed than honest ones. On the one hand this might be due to the fact that dishonest agents always lie very frequently and thereby produce a fake image of themselves, whereas honest agents only suffer from the Cassandra syndrome now and then. However, there might be another self-amplifying effect: as already explained, the others can not judge dishonest agents very well, which makes those good at identifying lies and, therefore, well-informed. However, once a dishonest agent is well-informed, this might in turn help to establish a high reputation, because being well-informed means also being able to target lies (including self-proposing lies) very successfully. This in turn makes others overestimate dishonest agents even more with the result of even worse lies, which brings us back to the origin of the circle. In other words, dishonest agents profit more from being misjudged, because for them, it is in the positive direction, which actually helps to self-amplify this effect and thereby gain even more informedness.
All in all, we observe this interesting effect: albeit intentional or not, hiding one’s own position and at the same time gathering information from others makes the agents well-informed and brings them into a strong position with respect to trading issues. This is also a well-known standard strategy in market business [
23] and naturally emerged in the reputation game simulation.
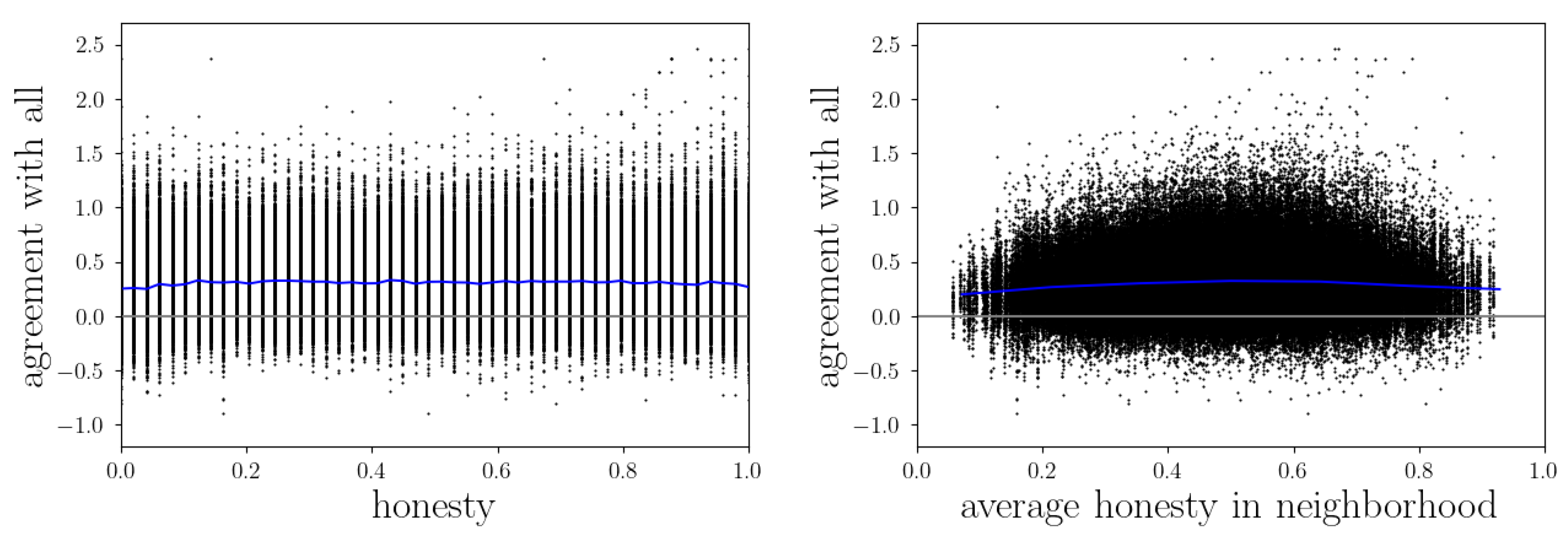
3.2.3. Honesty and Agreement
Another quantity we want to investigate is the agents’ agreement with others and how this is related to honesty. Analogous to informedness, the agreement between two agents
i and
j is defined as the alignment of their knowledge vectors:
In the left panel of
Figure 5 we see that on average, an agent’s honesty does not influence its agreement with others very much, but in order to achieve the highest agreement values, an agent has to be very honest. This can be explained because only when an agent gives others the chance to know their true opinions (and they believe them), they can adapt their belief states accordingly. Otherwise, if an agent hides its true worldview, the agreement will never become as high, since others can not adapt as precisely. When comparing both panels, one can conclude that these very honest agents that achieved the highest agreement values have only done so if their environments were quite honest, too. Again there might be too little data to say whether or not the highest agreement values would emerge in the most honest groups because it is just more likely to end up in a moderately honest neighborhood. However, the calculation of the average honesty in an agent’s neighborhood excludes the honesty of that agent itself. Considering that, together with the knowledge that the high agreement values visible in
Figure 5 are achieved by very honest agents, we argue that indeed high agreement is only possible if both an agent itself and its environment are honest. The only reason why the peak in the right panel is not at the very right is that there are not many extremely honest agents in the simulation and, therefore, extremely honest neighborhoods with an extremely honest agent in the center are simply very rare. In other words, in extremely honest neighborhoods there has to be a less honest agent in its center, which causes the overall agreement to be lower.
Comparing
Figure 5 with
Figure 4, the question might arise why for agreements we see a benefit from honest communication, but for informedness we do not. This can be explained by the presence of the illusory truth effect, which we already found to emerge in the reputation game simulations in [
22]. It is that the evolving group opinion on which most of the agents agree at the end of a simulation is not necessarily the truth, or at least may deviate from the truth in some aspects. With this in mind, it is clear why agreement and informedness depend on different conditions. For agreement it is only important to find a consensus with others, i.e., revealing all information one has (and believing every received message) would be the optimal strategy, which obviously works best among honest agents. For informedness, however, the crucial point is to distinguish between true and false information, which does not depend on others’ honesties in the first place, but rather on the own ability to judge the environment correctly.