1. Introduction
In the field of nonextensive statistics,
q-normal distributions and the generalization,
q-exponential families, play an important role [
1,
2,
3]. Since Ohara first pointed out the correspondence between the
q-parameter of nonextensive statistics and the
-parameter of information geometry [
4,
5], the information geometric structure of
q-exponential families has been investigated [
6,
7,
8,
9,
10,
11,
12,
13,
14].
On a set of probability distributions, divergences are usually defined for a fixed
-parameter of the dualistic structure. Using those results, we defined an extended divergence on a foliation by sets of probability distributions, setting different
-parameters on each leaf. In particular, we treated a foliation by deformed probability simplexes [
15].
In this paper, we also study deformed probability simplexes corresponding to sets of escort distributions with
q-parameters, which satisfy
for
-parameters of information geometry. We clarify the relationship among affine spaces, affine immersions and the extended divergence more than in our previous paper. A comparison with the extended divergence and the duo Bregman divergence used in machine learning is also described [
16].
First, we explain the dualistic structures, -divergences, and the Tsallis relative entropy on the probability simplex, using the concept of affine geometry and information geometry. The relationship between an -parameter and the Tsallis q-parameter is stated. Next, we describe the dualistic structures and the divergences generated by affine immersions on the deformed probability simplexes corresponding to sets of escort distributions. It also includes topics about Hessian manifolds and their level surfaces. We then define an extended divergence on a foliation by deformed probability simplexes. Finally, we propose a new decomposition of an extended divergence on the foliation.
2. The Tsallis Relative Entropy and the Kullback–Leibler Divergence on the Probability Simplex
In this section, we explain dualistic structures,
-divergences, and the Tsallis relative entropy on the probability simplex [
4,
5,
12].
Let
be an
-dimensional real affine space and
be the canonical affine coordinate system on
, i.e.,
, where
is the canonical flat affine connection on
. Let
be a simplex in
defined by
If
are regarded as probabilities of
states,
is called the
n-dimensional probability simplex. Let
be an affine coordinate system on
defined by
for
, and
be a frame of a tangent vector field on
.
The Fisher metric
on
is defined by
where
is the Kronecker’s delta. We define an
-connection
on
by
where
if
, and
if others. Then, the Levi–Civita connection
∇ of
g coincides with
. For
, we have
where
is the set of all smooth tangent vector fields on
. Then,
is called the dual connection of
. For each
,
is torsion-free and
is symmetric. Therefore, the triple
is a statistical manifold, and
the dual statistical manifold of it.
Note that affine connections and in Equations (4)–(6) are the dual connection and the canonical connection, respectively.
It is known that when
, the curvature of the statistical manifold
is a constant value
Therefore, the curvature of the dual statistical manifold
is also
. Iff
, the curvature of
is zero, and
is called the dually flat structure.
For
, an
-divergence
on
is often defined by
If
, it holds that
for the Tsallis relative entropy
on
defined by
where
is the q-logarithmic function defined by
Refs. [
1,
2]. The Tsallis relative entropy
converges to the Kullback–Leibler divergence as
, because
. In the information geometric view, the
-divergence
converges to the Kullback–Leibler divergence as
.
For the Tsallis q-parameter, the curvature of the statistical manifold is .
3. Divergences Generated by Affine Immersions as Level Surfaces
In this section, we describe the general theory of affine immersions and divergences related to level surfaces of the Hessian domain.
If the Hessian
of a function
on a domain
is non-degenerate, the triple
is called a Hessian domain. A statistical manifold is said to be flat if the curvature tensor of its affine connection vanishes. A flat statistical manifold is locally a Hessian domain. Conversely, a Hessian domain is a flat statistical manifold [
12,
17].
In a previous study, we show the following theorem on the level surfaces of a Hessian function.
Theorem 1 ([
18])
. Let M be a simply connected n-dimensional level surface of φ on an -dimensional Hessian domain with a Riemannian metric and suppose that . If we consider a flat statistical manifold, is a 1-conformally flat statistical submanifold of , where D and g denote the connection and the Riemannian metric on M induced by and , respectively. Here, “1-conformally flat” represents the characterization of surfaces projected by a flat statistical manifold along dual coordinates. We continue to explain the terms used in Theorem 1 and the outline of the proof.
For
, statistical manifolds
and
are
-conformally equivalent if there exists a function
on
N such that
If
is 1-conformally equivalent to a flat statistical manifold
,
is called a 1-conformally flat statistical manifold. A statistical manifold
is 1-conformally flat iff the dual statistical manifold
is
-conformally flat [
19].
In terms of affine geometry,
and
are
-conformally equivalent if and only if
and
are projectively equivalent [
20,
21].
For an -dimensional Hessian domain , an n-dimensional level surface of has the dualistic structure as the statistical submanifold structure. On the other hand, the level surface also has the structure induced by the affine immersion. It is essential for Theorem 1 that the statistical submanifold structure coincides with the dualistic structure by the affine immersion on a level surface of .
For
, let
x be the canonical immersion of an
n-dimensional level surface
M into
. Let
E be a transversal vector field on
M defined by
where
is the gradient vector field of
on
defined by
For an affine immersion
and the canonical flat affine connection
on
, the induced affine connection
, the affine fundamental form
, the shape operator
and the transversal connection form
on
M are defined by
See [
21,
22]. Then,
and
coincide with the restricted affine connection of
and the restricted Riemannian metric of
, respectively. For the level surface
M, the transversal connection form satisfies that
. Therefore,
it is called the equiaffine immersion. It is known that a simply connected statistical manifold can be realized in
by a non-degenerate equiaffine immersion iff it is 1-conformally flat [
19]. Thus, Theorem 1 holds.
Next, we introduce a divergence on a Hessian domain, treating it as a flat statistical manifold.
The canonical divergence
of a Hessian domain
is defined by
where
is the gradient mapping from
to the dual affine space
, i.e.,
and {
} is the dual affine coordinate system of {
}. The Legendre transform
of
is defined by
See [
12].
Let
be the conormal immersion for the affine immersion
defined by Equation (
11), 12. By the definition of a conormal immersion,
satisfies that
where
is the pairing of
and
. It is known that the conormal immersion
coincides with the restriction of the gradient mapping
to the level surface
M.
The next definition is given in relation to affine immersions and divergences.
Definition 1 ([19]).Let be a 1-conformally flat statistical manifold realized by a non-degenerate affine immersion into , and w the conormal immersion for v. Then the divergence of is defined byThe definition is independent of the choice of a realization of . The divergence
is referred to as Kurose geometric divergence in affine geometry and as Fenchel–Young divergence in the machine learning community [
23,
24]. Since an
n-dimensional level surface
M of
is a 1-conformally flat statistical manifold realized by a non-degenerate affine immersion
,
on
M is as follows:
Let be the restriction of the canonical divergence to as a statistical submanifold of . From Equations (15), (17) and (18), the next theorem holds.
Theorem 2 ([
20])
. For a 1
-conformally flat statistical submanifold of , two divergences and coincide. 4. Deformed Probability Simplexes and Escort Distributions Generated by Affine Immersions
In this section, we explain dualistic structures on deformed probability simplexes, which correspond to sets of escort distributions via affine immersion.
We set
,
for
, where
and
be the probability simplex and the canonical affine coordinate system on
, respectively. For
states
on
and
, if each probability
satisfies
the probability distribution
is called the escort distribution [
1,
2], where
is
powered by
q.
It realizes the dualistic structure of a set of escort distributions via the affine immersion into
[
4,
5]. For
, let
be the affine immersion of
into
defined by
Then, the escort distribution
is also represented as follows:
For a function
on
defined by
the image
is a level surface of
satisfying
. For
, the Hessian matrix of the function
is positive definite on
. Then,
induces the Hessian structure
. By definition
the tetrad
is the dually flat structure. The connection
coincides with the Levi–Civita connection of the Riemannian metric
.
We denote by
D and
the restricted
and
on
, and induce the dualistic structure of
as the submanifold structure of
. From the discussion in
Section 3,
coincides with the dualistic structure induced by the equiaffine immersion
, where
for the gradient vector field
of
on
defined by
The pullback of
to
is
-conformally equivalent to
defined by Equations (3)–(5). In addition,
has a constant curvature
[
5].
On
, the restricted divergence
from the canonical divergence of
coincides with the geometric divergence by Equation (
18) from the affine immersion
. For an affine coordinate system
on
defined by
the divergence
of
is described as
In addition, the pullback divergence of
to
coincides with
and the Tsallis relative entropy
[
4].
At the end of this section, we mention the divergence of
. By Equation (
17), the Legendre transform
of
is
By Equations (15) and (16), the canonical divergence
of
is defined by
represented by the same symbol
of
.
5. Extended Divergence on a Foliation by Deformed Probability Simplexes
Previous sections described the divergence for each fixed
q and each fixed
. This section defines an extended divergence on a foliation by deformed probability simplexes
for all
, and shows the divergence decomposition theorem. The contents of our paper [
15] are included but are explained in detail by the setting of affine geometry.
To give the proximity of q-escort distributions with different q-parameters, we define an extended divergence on a foliation by deformed probability simplexes as follows.
Definition 2. Let , which corresponds to a foliation . We call a function on defined by Equation (31) an extended divergence on a foliation by deformed probability simplexes. The
i-th component of the conormal immersion of
is
. By the right-hand side of Equation (
27), the dual coordinate of
b, denoted by
, satisfies that
Therefore, we consider
as the dual simplex of
for
. As
,
is self dual [
4]. Note that the
i-th component of the dual coordinate of
b is denoted by
in [
15].
On the extended divergence, the next proposition holds.
Proposition 1. An extended divergence on of satisfies that:
(i) If ,whereis the divergence ofby Equation (28),is an α-divergence defined by Equation (7), and . (ii) In the case of ,and if and only if , Proof. If
,
. By Equations (28) and (31),
Then, (i) holds. If
, it holds that
because
are induced by the definition of
. In addition,
and
are convex surfaces centered on the origini of
, and the surfaces
closer to the origin than
. Then,
. Thus, (ii) holds. □
We define the
extended dual divergence of
as follows;
where
is the Legendre transform of
for
. Then, the following holds.
Proposition 2. The functions and satisfy that Proof. By the definition of the Legendre transform, we have
□
The extended divergence is related to the duo Bregman (pseudo-)divergence, where the parameters also define the convex functions [
16]. To work with the entire parametrized probability distribution families and to explore the application of divergences, we must investigate their relationship.
6. Decomposition of an Extended Divergence
In this section, we explain the orthogonal foliation of . Next, we give a decomposition of an extended divergence along the orthogonal leaf and the original leaf.
For the foliation
, we consider the flow on
defined using the following equation.
where a function
on
takes the
i-th component of the dual coordinate on
as Equation (
27) for each
. An integral curve of Equation (
35) is orthogonal to
for each
q with respect to the pairing
. The set of integral curves becomes the orthogonal foliation of
. We denote it by
.
Translating into the primal coordinate system, we have the next equation.
where
is the inverse matrix of
. The right-hand side of Equation (
37) is calculated using Equations (11) and (12) for
. A leaf of
is an integral curve of the vector field
that takes the value
on
for each
q.
The following theorem is on the decomposition of the extended divergence.
Theorem 3. Let be the probability simplex, and the 1-conformally flat statistical manifold generated by the affine immersion , where is defined as, , , and is the restriction of to . Let , , and . If there exists an orthogonal leaf that includes b and c, we havewhere is the dual coordinate of for each q. Proof. From
, it holds that
, where
. By the definition in Equations (22) and (23), we have
□
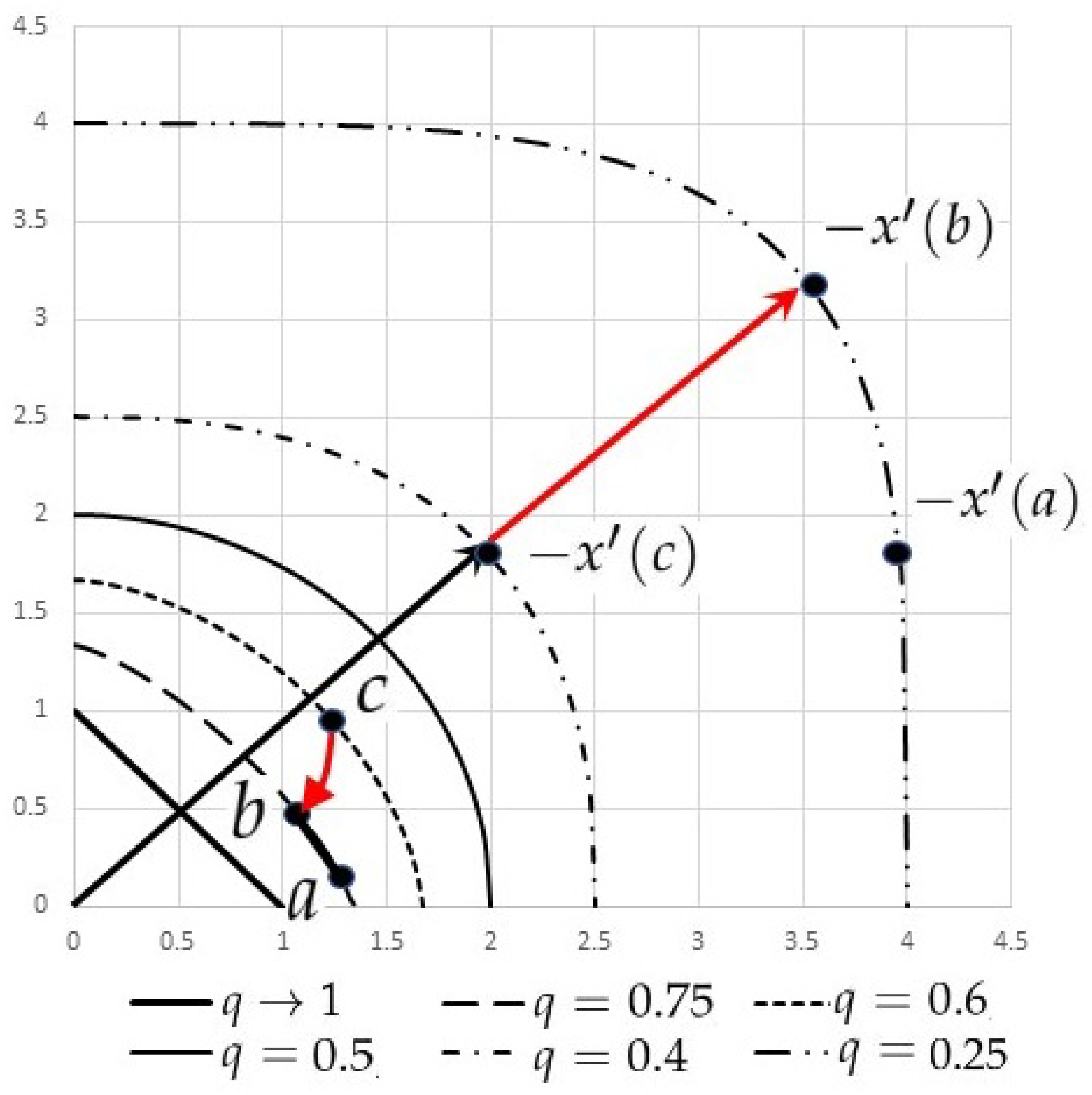
See
Figure 1 for a decomposition of extended divergence and graphs of deformed simplexes
.
A decomposition similar to Equation (
39) is also available on a foliation by Hessian level surfaces of one Hessian manifold [
20]. Theorem 3 generalizes the previous decomposition.
Finally, we describe the gradient flow on a leaf using the extended divergence.
Theorem 4. For a submanifold of , we denote by an affine coordinate system on such that , , and set , . For a fixed point , the gradient flow on defined byconverges to the unique point , where is a variable point parametrized as . Proof. By Theorem 3, for any
, there exists
such that
Equation (
40) is described by the dual coordinate system
on
as follows;
On
, from Prop. 1.(i),
coincides with the geometric divergence
, generated by the affine immersion
. The geometric divergence generates the dual coordinate
such that
,
, to be derived by
[
19]. Then, it holds that
and that
where
is an initial point of Equation (
40). Then, the gradient flow of Equation (
40) converges to
following a geodesic for the dual coordinate system. □
The gradient flow similar to Equation (
40) has been provided on a flat statistical submanifold [
25]. The similar one on a Hessian level surface, i.e., a 1-conformally statistical submanifold, has been given in [
20]. Theorem 4 generalizes the previous theorems on gradient flows.