Multifractal Analysis of MODIS Aqua and Terra Satellite Time Series of Normalized Difference Vegetation Index and Enhanced Vegetation Index of Sites Affected by Wildfires
Abstract
1. Introduction
2. Materials and Methods
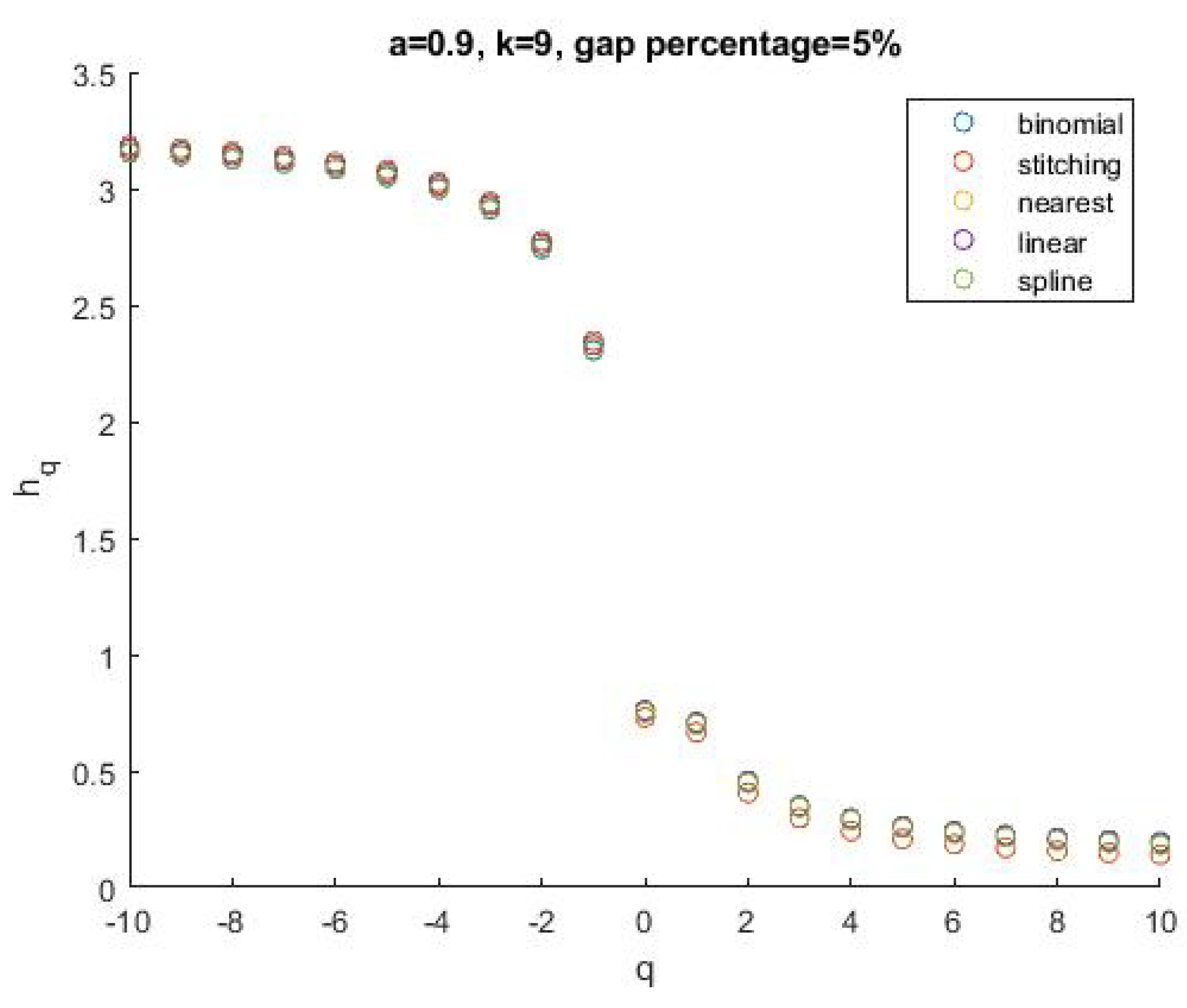
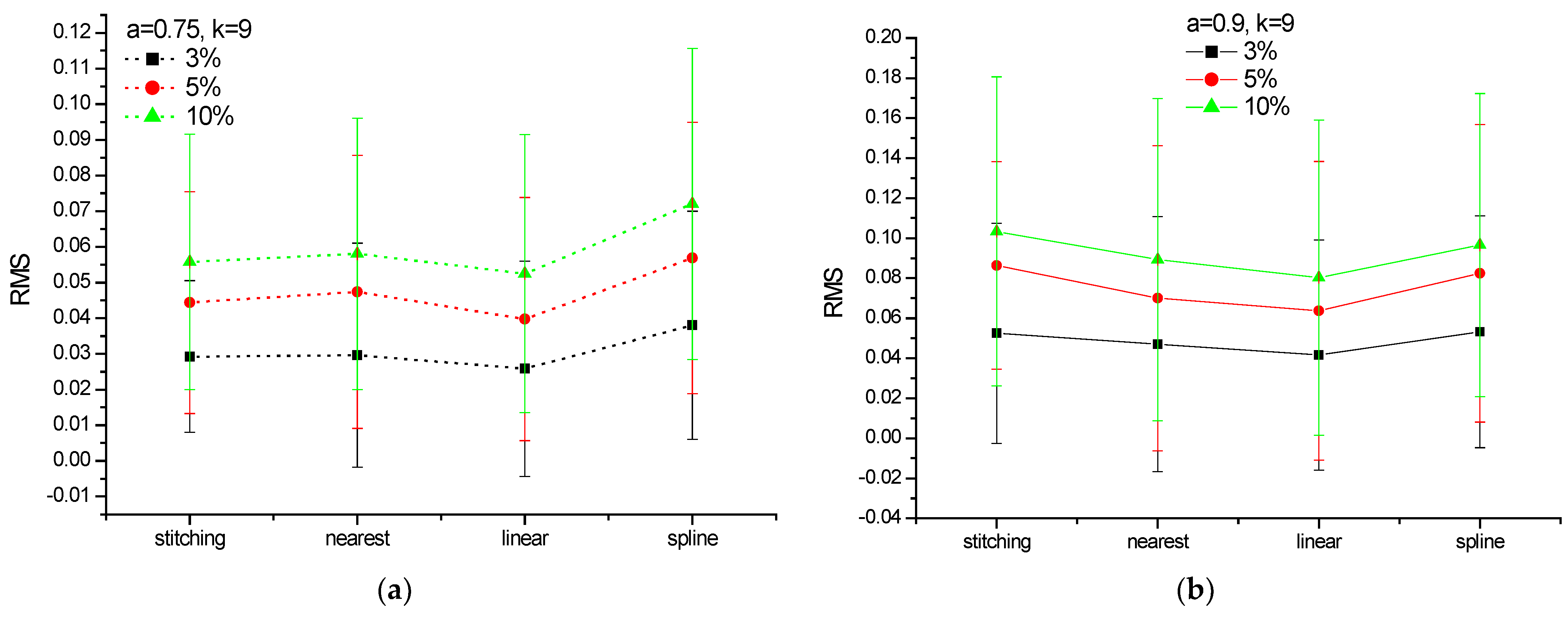
2.1. Data Preprocessing
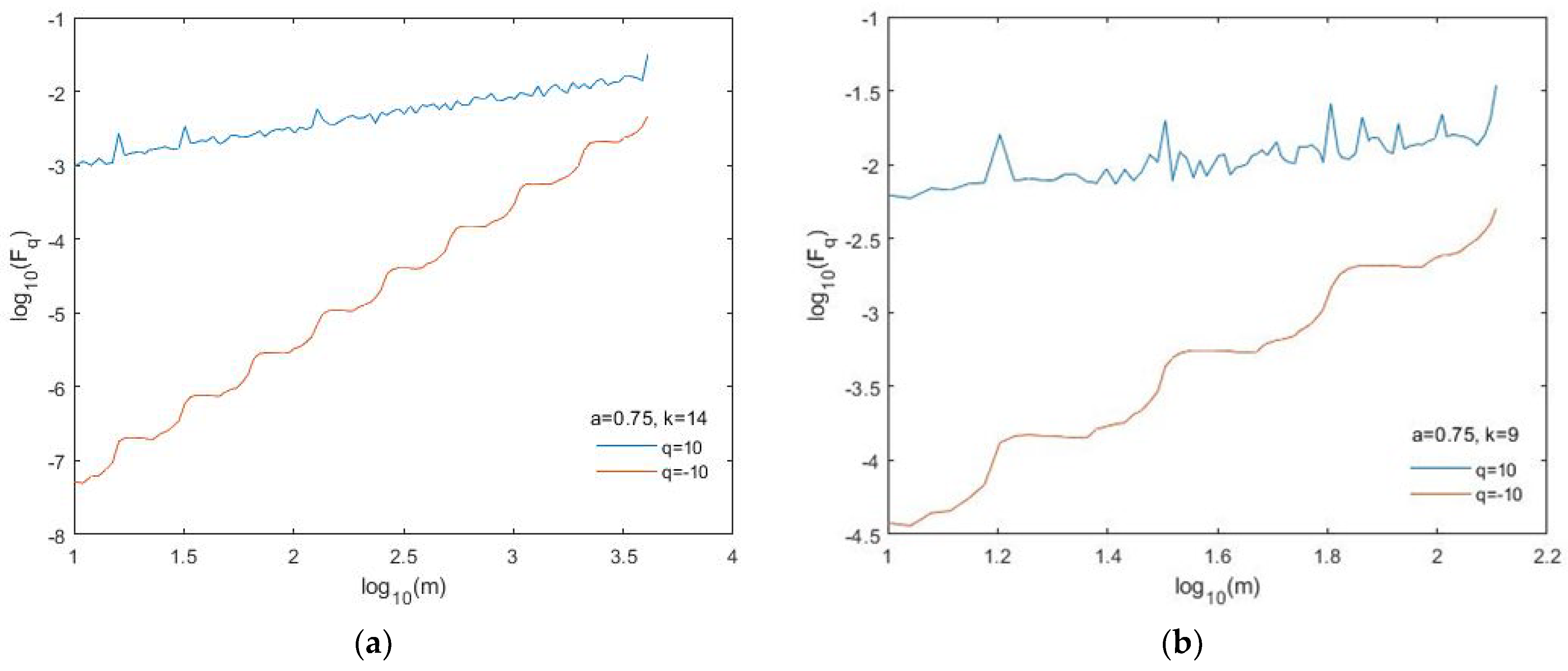
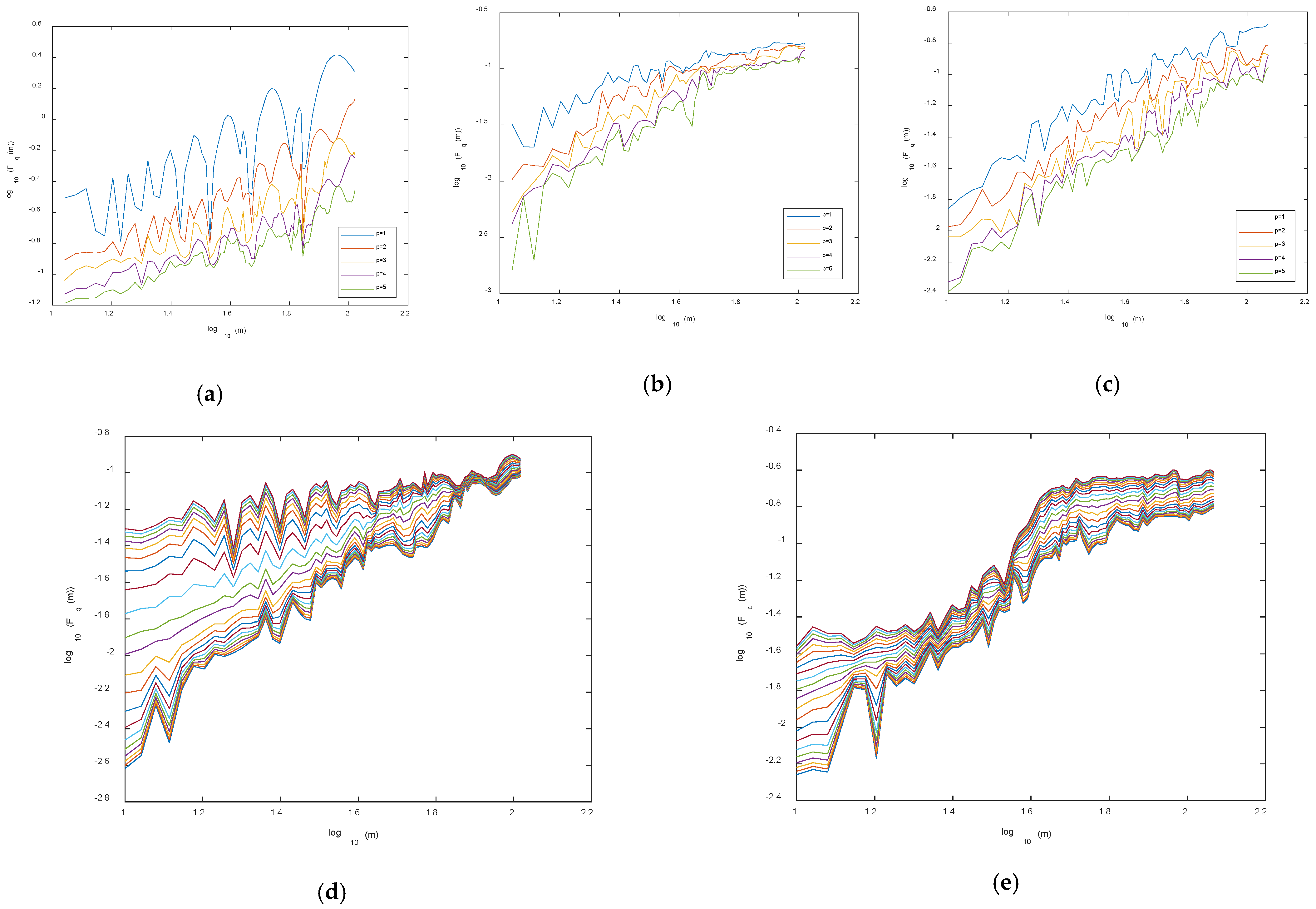
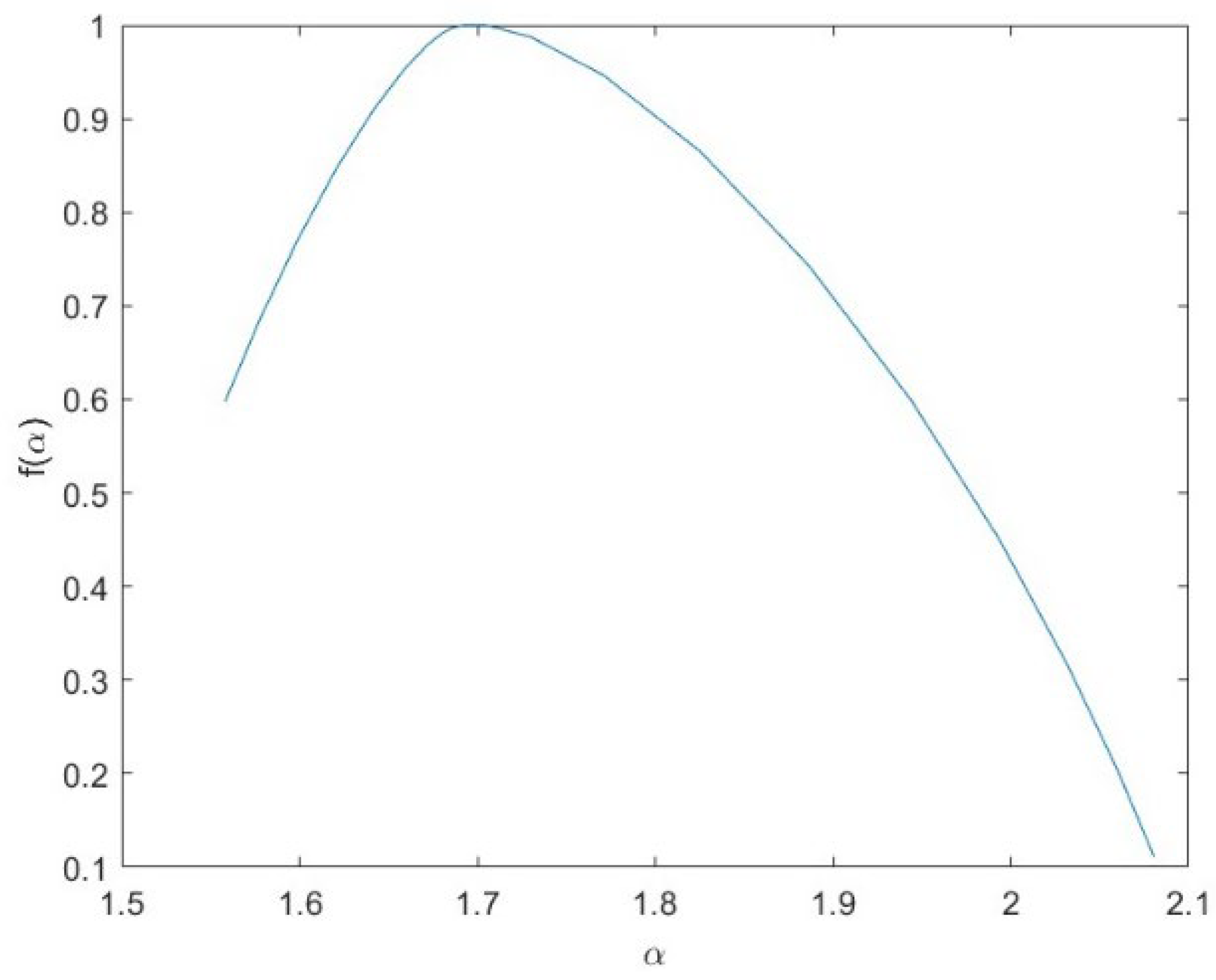
2.2. The Multifractal Detrended Fluctuation Analysis (MFDFA)
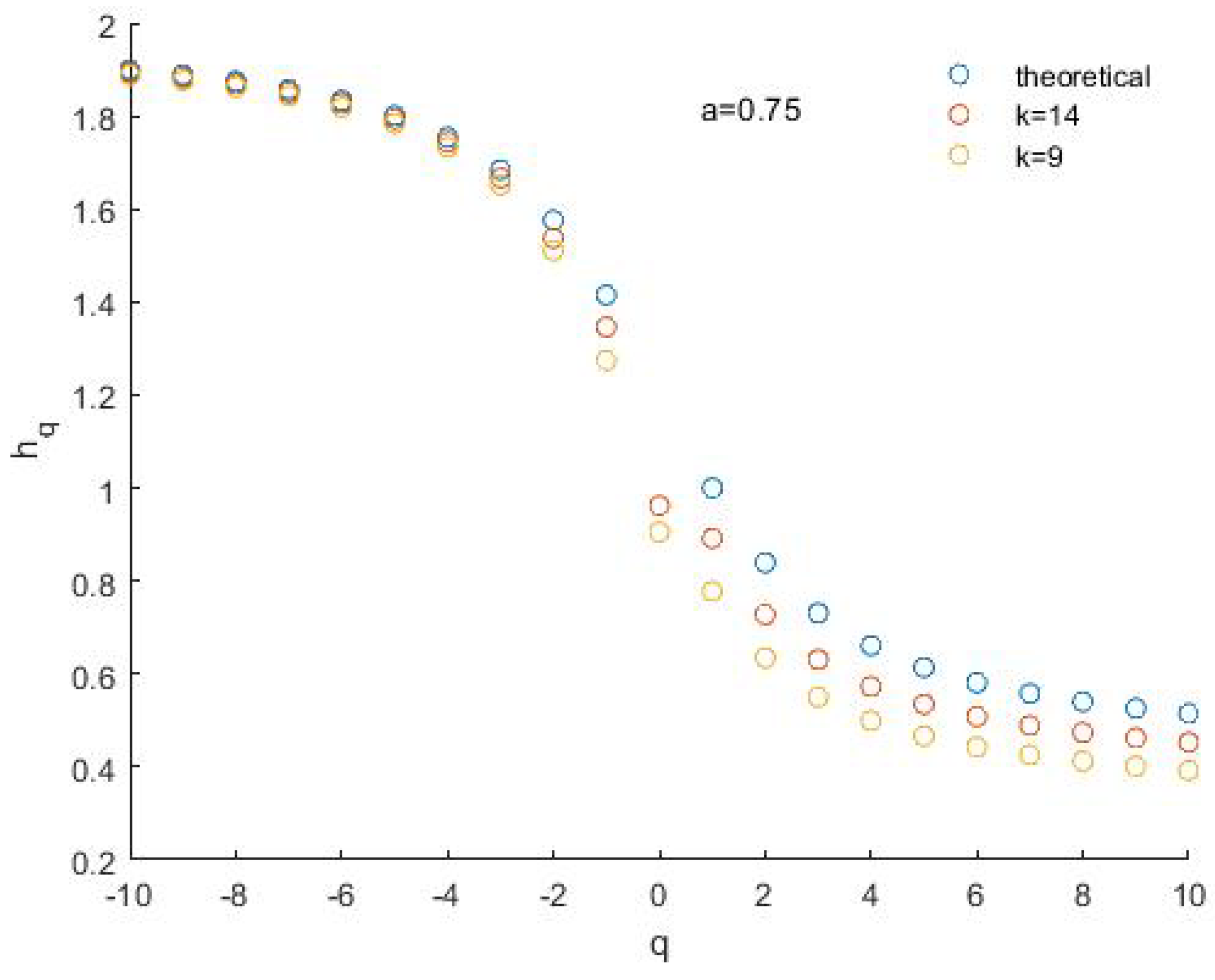
2.3. The Binomial Multifractal Model
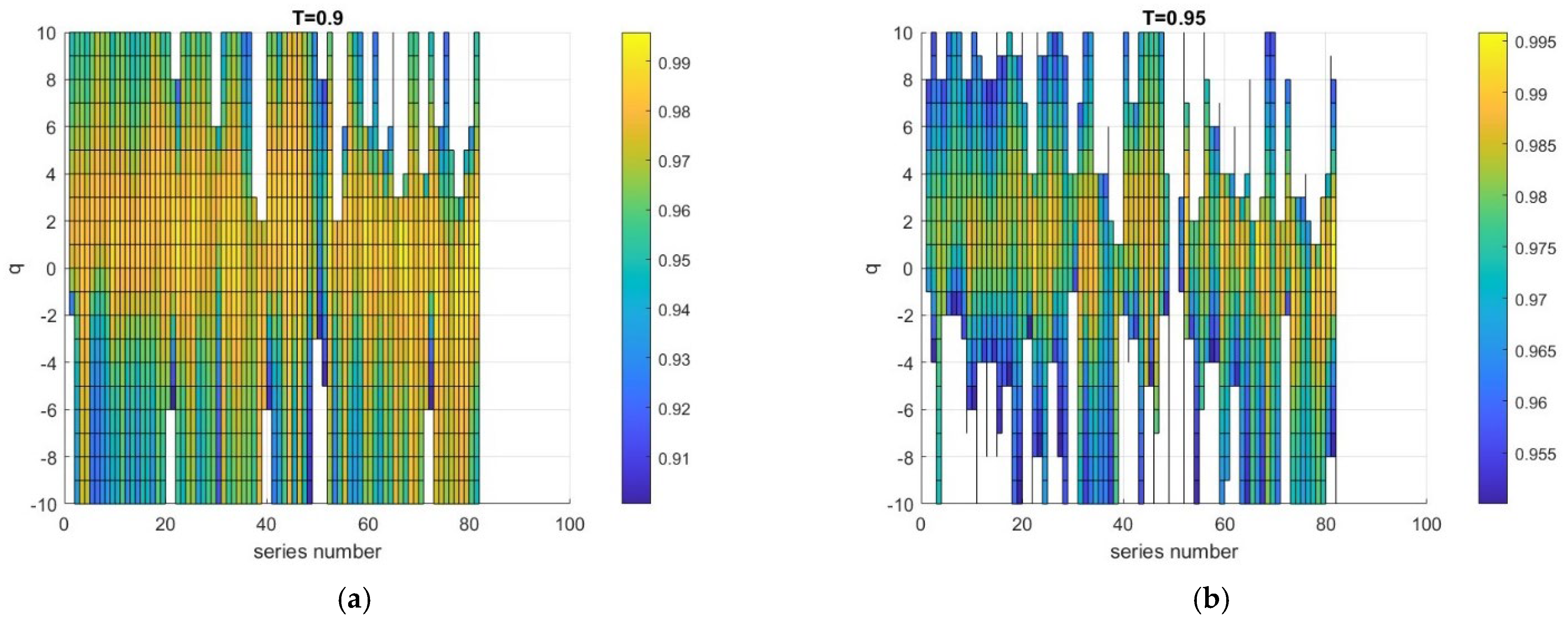
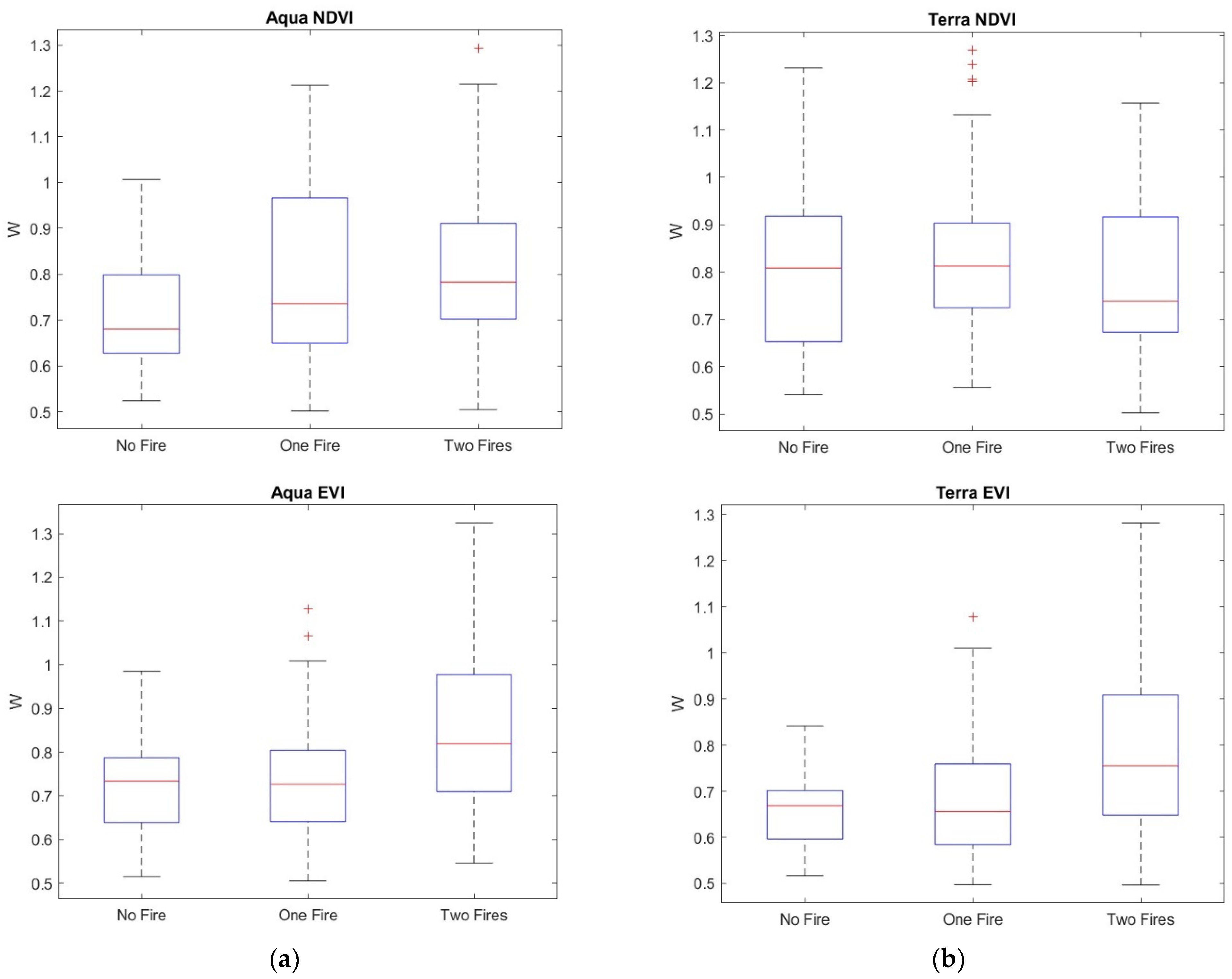
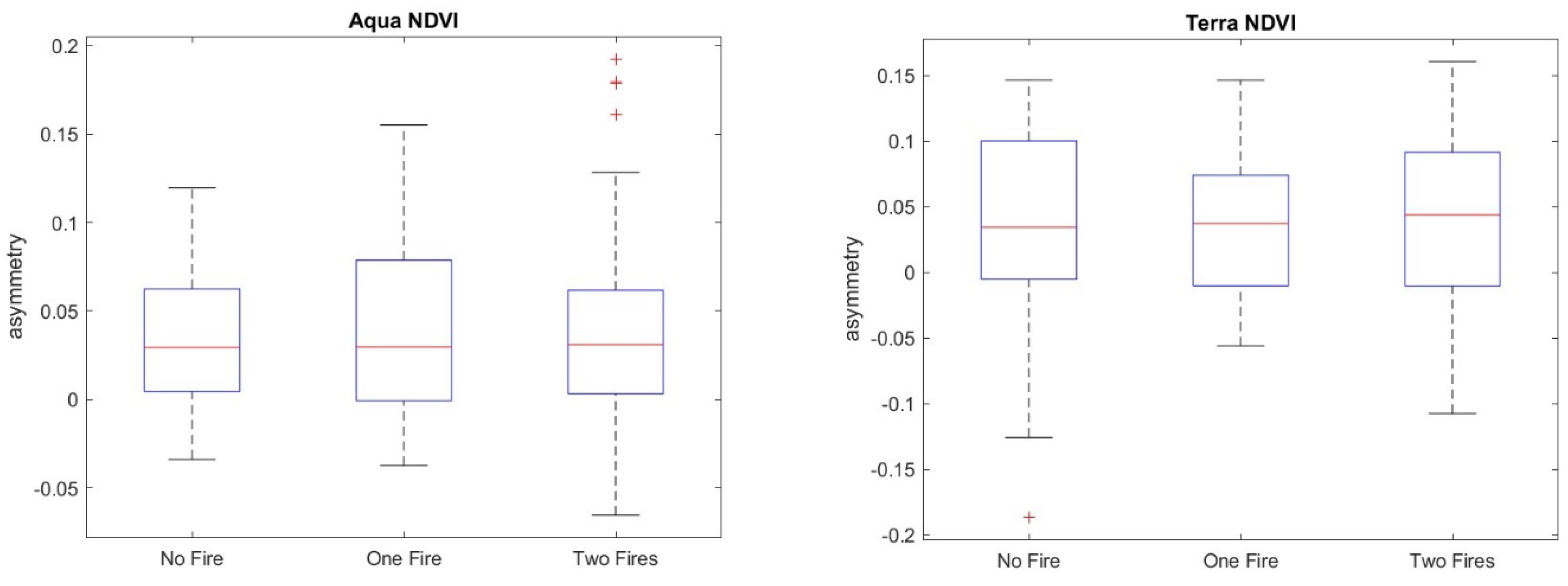
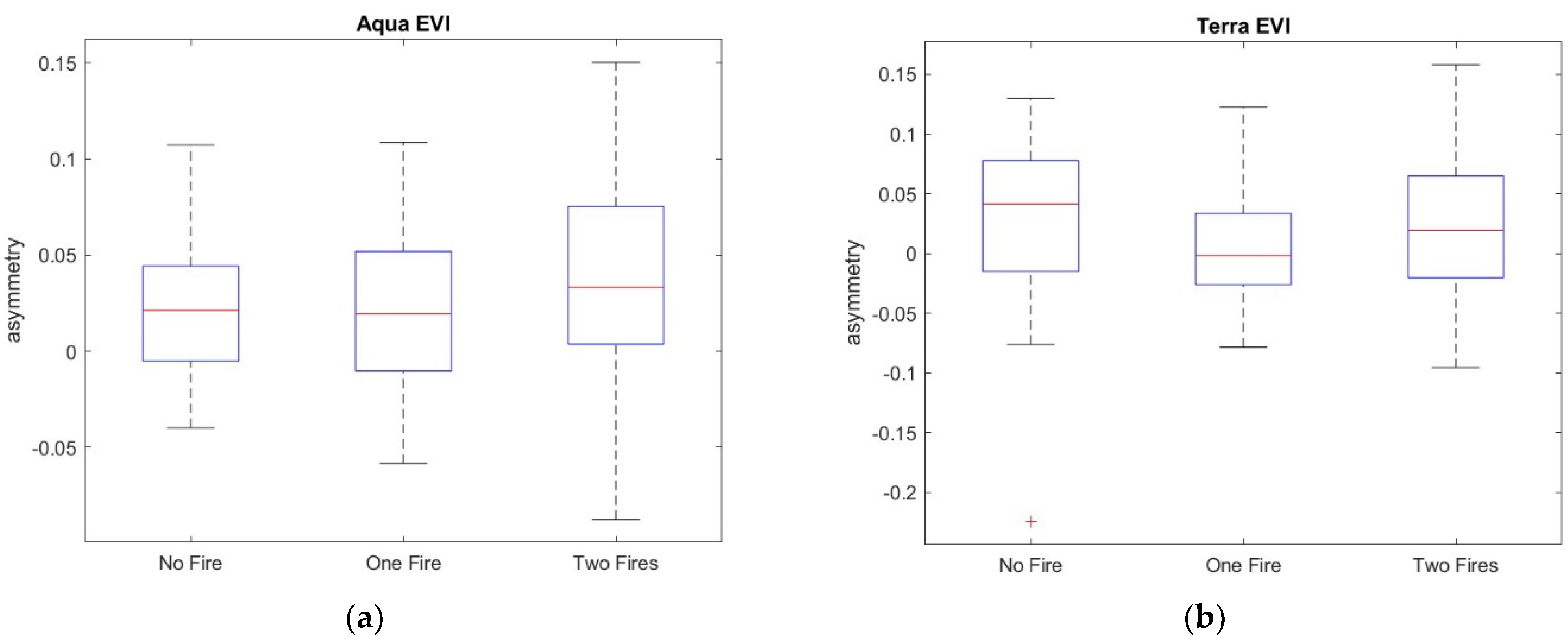
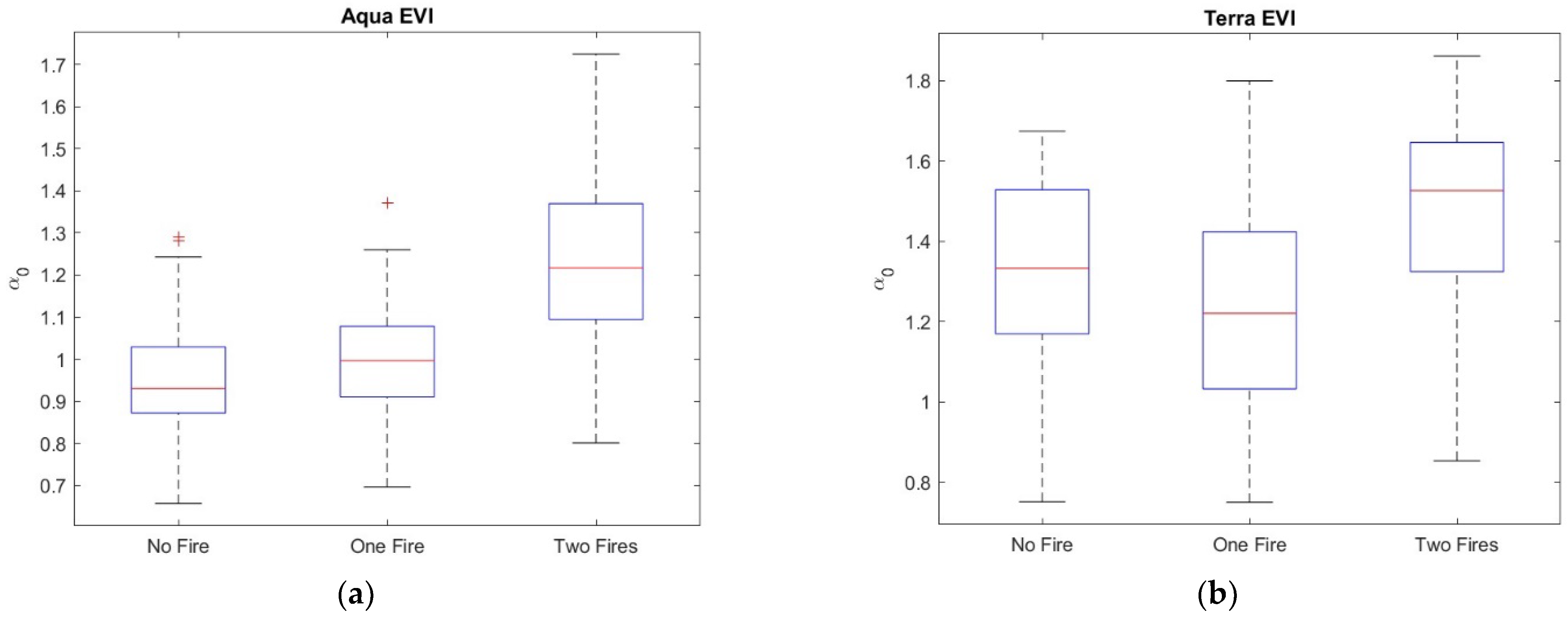
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yapp, G.; Walker, J.; Thackway, R. Linking vegetation type and condition to ecosystem goods and services. Ecol. Complex. 2010, 7, 292–301. [Google Scholar] [CrossRef]
- Lawley, V.; Lewis, M.; Clarke, K.; Ostendorf, B. Site-based and remote sensing methods for monitoring indicators of vegetation condition: An Australian review. Ecol. Indic. 2016, 60, 1273–1283. [Google Scholar] [CrossRef]
- Carvalheiro, L.C.; Bernardo, S.O.; Orgaz, M.D.M.; Yamazaki, Y. Forest Fires Mapping and Monitoring of current and past forest fire activity from Meteosat Second Generation Data. Environ. Model. Softw. 2010, 25, 1909–1914. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Uncertainty associated with model predictions of surface and crown fire rates of spread. Environ. Model. Softw. 2013, 47, 16–28. [Google Scholar] [CrossRef]
- Eastaugh, C.S.; Hasenauer, H. Deriving forest fire ignition risk with biogeochemical process modelling. Environ. Model. Softw. 2014, 55, 132–142. [Google Scholar] [CrossRef]
- French, N.H.F.; Kasischke, E.S.; Hall, R.J.; Murphy, K.A.; Verbyla, D.L.; Hoy, E.E.; Allen, J.L. Using Landsat data to assess fire and burn severity in the North American boreal forest region: An overview and summary of results. Int. J. Wildland Fire 2008, 17, 443–462. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Lentile, L.B.; Holden, Z.A.; Smith, A.M.S.; Falkowski, M.J.; Hudak, A.T.; Morgan, P.; Lewis, S.A.; Gessler, P.E.; Benson, N.C. Remote sensing techniques to assess active fire characteristics and post-fire effects. Int. J. Wildland Fire 2006, 15, 319–345. [Google Scholar] [CrossRef]
- FAO. Global Forest Fire Assessment 1990–2000. Available online: http://www.fire.uni-freiburg.de/programmes/un/fao/Wp55_eng.pdf (accessed on 6 October 2022).
- FAO. Global Forest Resources Assessment 2010; FAO: Rome, Italy, 2010. [Google Scholar]
- UNCCD. United Nations Convention to Combat Desertification; UNCCD: Paris, France, 1994. [Google Scholar]
- Diaz-Delgado, R.; Llorett, F.; Pons, X. Influence of fire severity on plant regeneration by means of remote sensing imagery. Int. J. Remote Sens. 2003, 24, 1751–1763. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Black, T.A.; Jarvis, P.G.; McCaughey, J.H.; Hall, F.G. High temporal resolution NDVI phenology from micrometeorological radiation sensors. J. Geophys. Res.-Atmos. 1999, 104, 27935–27944. [Google Scholar] [CrossRef]
- Lasaponara, R. Estimating interannual variations in vegetated areas of Sardinia island using SPOT/VEGETATION NDVI temporal series. IEEE Geosci. Remote Sci. 2006, 3, 481–483. [Google Scholar] [CrossRef]
- Lasaponara, R. Estimating spectral separability of satellite derived parameters for burned areas mapping in the Calabria region by using SPOT-Vegetation data. Ecol. Model. 2006, 196, 265–270. [Google Scholar] [CrossRef]
- Lasaponara, R. Geospatial analysis from space: Advanced approaches for data processing, information extraction and interpretation. Int. J. Appl. Earth Obs. 2013, 20, 1–3. [Google Scholar] [CrossRef]
- Xie, Z.; Song, W.; Ba, R.; Li, X.; Xia, L. A Spatiotemporal Contextual Model for Forest Fire Detection Using Himawari-8 Satellite Data. Remote Sens. 2018, 10, 1992. [Google Scholar] [CrossRef]
- Ba, R.; Chen, C.; Yuan, J.; Song, W.; Lo, S. SmokeNet: Satellite Smoke Scene Detection Using Convolutional Neural Network with Spatial and Channel-Wise Attention. Remote Sens. 2019, 11, 1702. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS vegetation indices. In Land Remote Sensing and Global Environmental Change; Springer: Berlin/Heidelberg, Germany, 2010; pp. 579–602. [Google Scholar]
- Testa, S.; Soudani, K.; Boschetti, L.; Mondino, E.B. MODIS-derived EVI, NDVI and WDRVI time series to estimate phenological metrics in French deciduous forests. Int. J. Appl. Earth Obs. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Analysis of time-scaling properties in forest-fire sequence observed in Italy. Ecol. Model. 2010, 221, 90–93. [Google Scholar] [CrossRef]
- Telesca, L.; Lanorte, A.; Lasaponara, R. Investigating dynamical trends in burned and unburned vegetation covers using SPOT-VGT NDVI data. J. Geophys. Eng. 2007, 4, 128–138. [Google Scholar] [CrossRef]
- Telesca, L. Fractal Methods in the Investigation of the Time Dynamics of Fires: An Overview. In Fractal Solutions for Understanding Complex Systems in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2016; pp. 117–152. [Google Scholar]
- Telesca, L.; Lasaponara, R. Discriminating dynamical patterns in burned and unburned vegetational covers by using SPOT-VGT NDVI data. Geophys. Res. Lett. 2005, 32, L21401. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Vegetational patterns in burned and unburned areas investigated by using the detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2006, 368, 531–535. [Google Scholar] [CrossRef]
- Li, X.; Lanorte, A.; Lasaponara, R.; Lovallo, M.; Song, W.; Telesca, L. Fisher–Shannon and detrended fluctuation analysis of MODIS normalized difference vegetation index (NDVI) time series of fire-affected and fire-unaffected pixels. Geomat. Nat. Hazards Risk 2017, 8, 1342–1357. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS Collection 6 Land Cover product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Fornacca, D.; Ren, G.; Xiao, W. Evaluating the Best Spectral Indices for the Detection of Burn Scars at Several Post-Fire Dates in a Mountainous Region of Northwest Yunnan, China. Remote Sens. 2018, 10, 1196. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Ba, R.; Song, W.; Lo, S.; Xie, Z. Spectral Characteristic Analysis of Burned Area Based on MODIS Data. In Proceedings of the Asia-Oceania Symposium on Fire Science and Technology, Taipei, Taiwan, 21–25 October 2018; pp. 391–404. [Google Scholar]
- Ba, R.; Song, W.; Lovallo, M.; Zhang, H.; Telesca, L. Informational analysis of MODIS NDVI and EVI time series of sites affected and unaffected by wildfires. Phys. A Stat. Mech. Its Appl. 2022, 604, 127911. [Google Scholar] [CrossRef]
- ORNL DAAC. MODIS and VIIRS Land Products Global Subsetting and Visualization Tool. 2018. Available online: https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1379 (accessed on 6 October 2022).
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://lpdaac.usgs.gov/products/mod13q1v006/ (accessed on 6 October 2022).
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Drożdż, S.; Oświȩcimka, P. Detecting and interpreting distortions in hierarchical organization of complex time series. Phys. Rev. E 2015, 91, 030902. [Google Scholar] [CrossRef]
- Grech, D.; Pamuła, G. On the multifractal effects generated by monofractal signals. Phys. A Stat. Mech. Its Appl. 2013, 392, 5845–5864. [Google Scholar] [CrossRef]
- Monterrubio-Velasco, M.; Lana, X.; Dolors Martínez, M.; Ramón Zúñiga, F.; de la Puente, J. Evolution of the multifractal parameters along different steps of a seismic activity. The example of Canterbury 2000–2018 (New Zealand). AIP Adv. 2020, 10, 115109. [Google Scholar] [CrossRef]
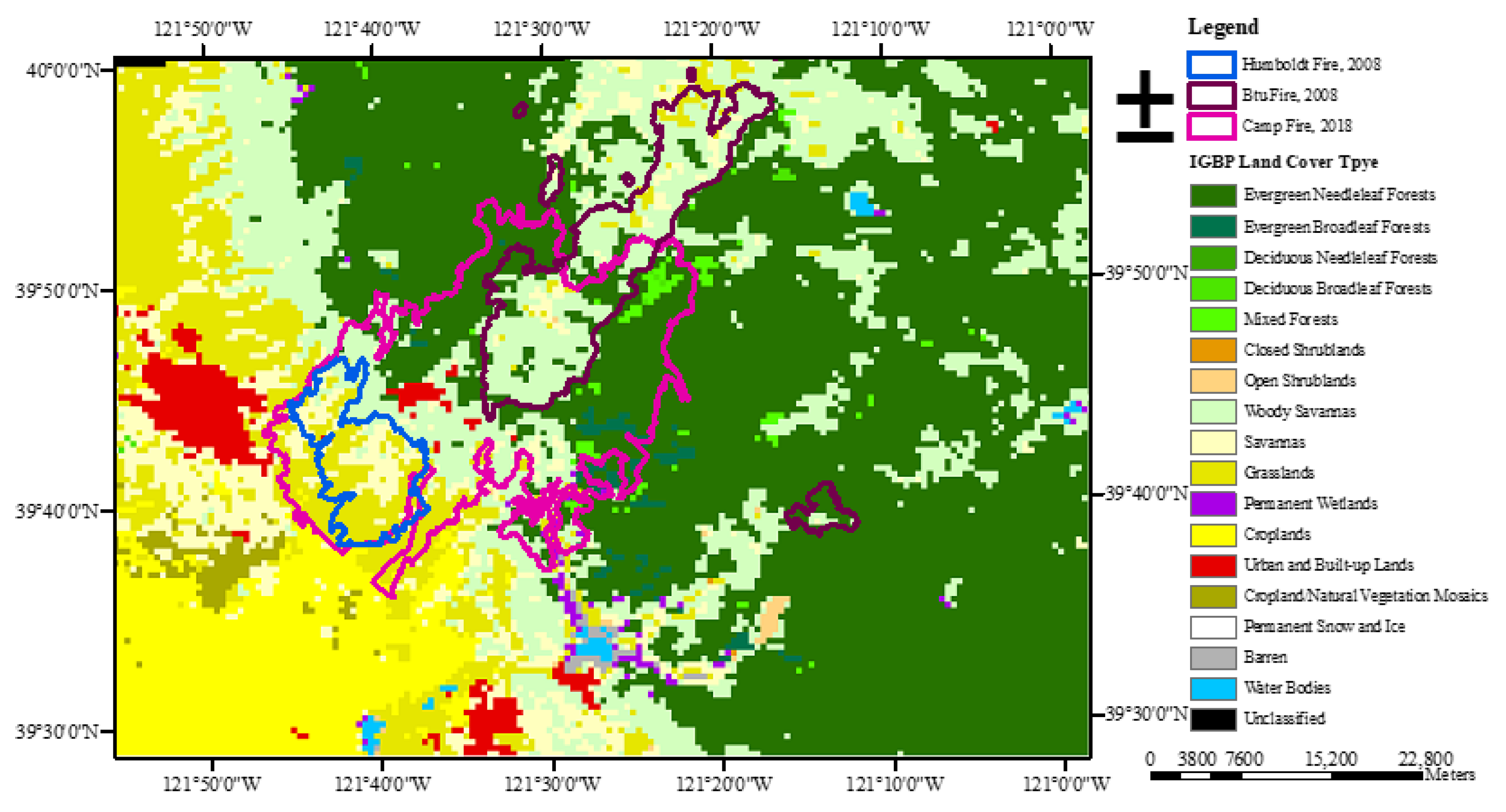
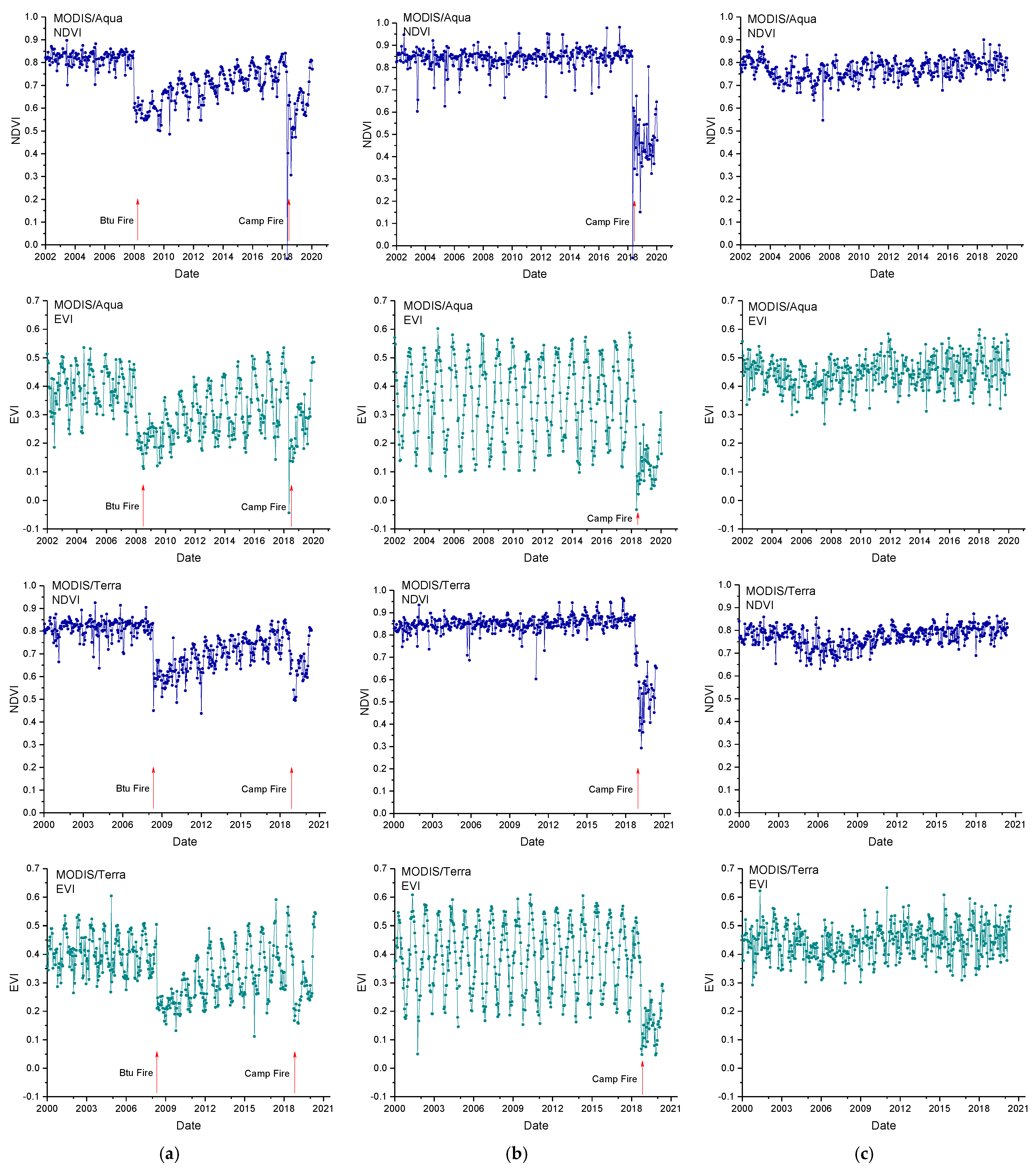


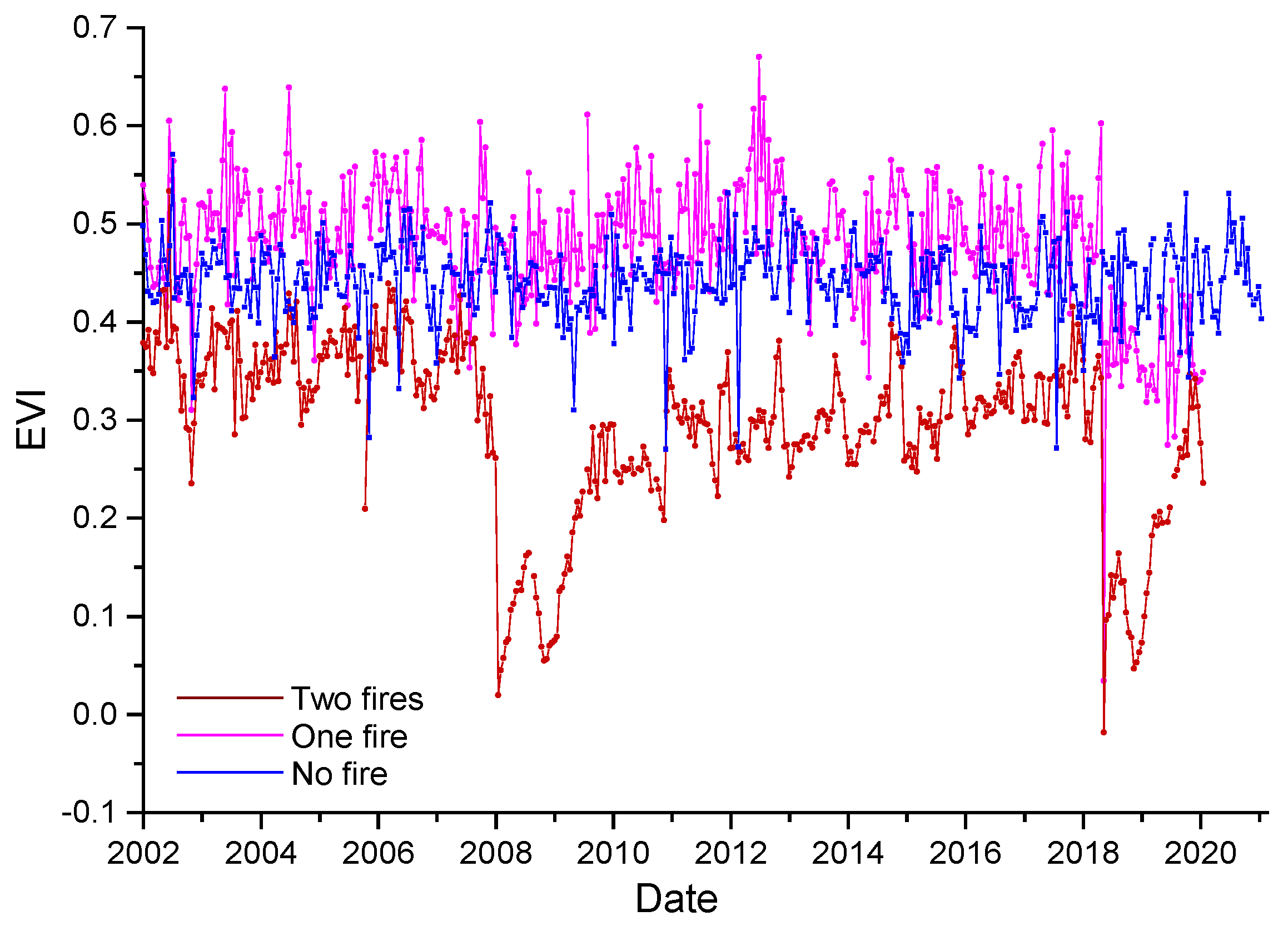
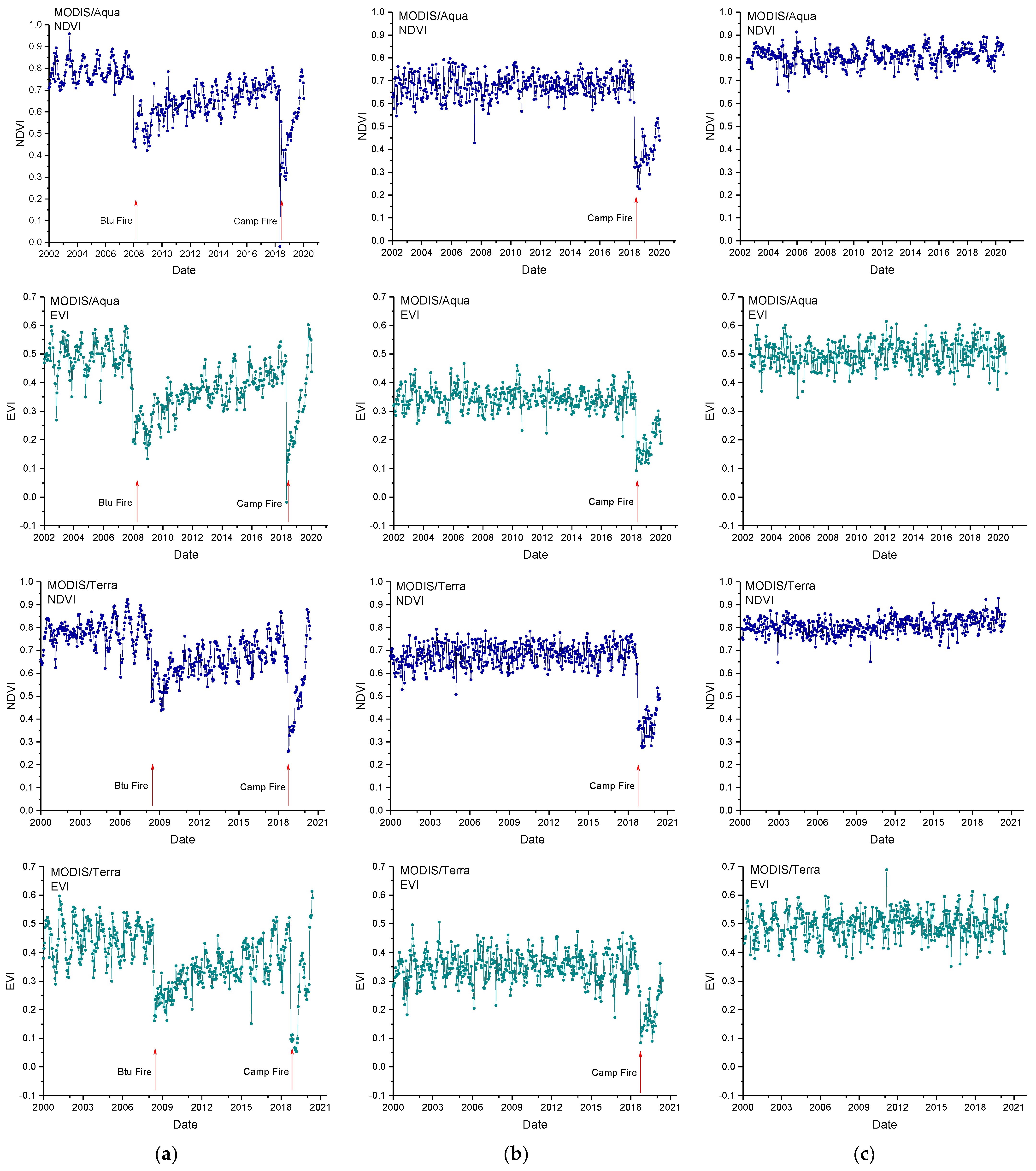



| Wildfire Event | Duration | Cause | Burned Area (Acres) | Tree Coverage (%) |
|---|---|---|---|---|
| Humboldt Fire | 11–21 June 2008 | Arson | 23,344 | Grasslands 54.59%, Savannas 32.02%, Woody Savannas 12.86% |
| Btu Fire | 21 June–29 July 2008 | Lightning strikes | 57,815 | Woody Savannas 59.94%, Evergreen Needleleaf Forests 23.78%, Savannas 7.29%, Grasslands 5.71% |
| Camp Fire | 8–25 November 2018 | Electrical transmission lines | 153,336 | Evergreen Needleleaf Forests 37.20%, Woody Savannas 31.20%, Grasslands 16.06%, Savannas 9.38% |
| VI Product | VI | Spatial Resolution (m) | Frequency (Days) | Temporal Extent (Year) | Sensor/Satellite |
|---|---|---|---|---|---|
| MOD13Q1 | NDVI, EVI | 250 | 16 | 2000–2020 | MODIS/Terra |
| MYD13Q1 | NDVI, EVI | 250 | 16 | 2002–2020 | MODIS/Aqua |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire | 54 | 39 | 37 | 48 |
| One Fire | 136 | 62 | 174 | 113 |
| Two Fires | 149 | 80 | 184 | 138 |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire–One Fire | 0.073337 | 0.001878 | 0.666646 | 0.778663 |
| One Fire–Two Fires | 1.83 × 10−23 | 0.325468 | 6.25 × 10−10 | 6.94 × 10−14 |
| No Fire–Two Fires | 3.20 × 10−16 | 2.06 × 10−6 | 0.001233 | 3.14 × 10−5 |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire–One Fire | 0.897719 | 0.042757 | 0.321087 | 0.960532 |
| One Fire–Two Fires | 6.95 × 10−11 | 0.595574 | 3.14 × 10−7 | 0.688014 |
| No Fire–Two Fires | 8.71 × 10−9 | 0.007061 | 1.77 × 10−7 | 0.679548 |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire–One Fire | 0.733290 | 0.045961 | 0.288707 | 0.348462 |
| One Fire–Two Fires | 7.66 × 10−10 | 0.669236 | 1.26 × 10−6 | 0.941305 |
| No Fire–Two Fires | 3.04 × 10−8 | 0.010015 | 7.83 × 10−7 | 0.230172 |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire–One Fire | 0.909562 | 0.562129 | 0.194883 | 0.904868 |
| One Fire–Two Fires | 0.001069 | 0.745943 | 0.009704 | 0.711969 |
| No Fire–Two Fires | 0.003398 | 0.778580 | 0.790529 | 0.880401 |
| Aqua-EVI | Aqua-NDVI | Terra-EVI | Terra-NDVI | |
|---|---|---|---|---|
| No Fire–One Fire | 0.225453 | 3.77 × 10−4 | 0.125898 | 0.002197 |
| One Fire–Two Fires | 3.39 × 10−25 | 0.757963 | 8.55 × 10−13 | 1.70 × 10−8 |
| No Fire–Two Fires | 7.87 × 10−17 | 5.84 × 10−6 | 0.002117 | 2.45 × 10−13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ba, R.; Lovallo, M.; Song, W.; Zhang, H.; Telesca, L. Multifractal Analysis of MODIS Aqua and Terra Satellite Time Series of Normalized Difference Vegetation Index and Enhanced Vegetation Index of Sites Affected by Wildfires. Entropy 2022, 24, 1748. https://doi.org/10.3390/e24121748
Ba R, Lovallo M, Song W, Zhang H, Telesca L. Multifractal Analysis of MODIS Aqua and Terra Satellite Time Series of Normalized Difference Vegetation Index and Enhanced Vegetation Index of Sites Affected by Wildfires. Entropy. 2022; 24(12):1748. https://doi.org/10.3390/e24121748
Chicago/Turabian StyleBa, Rui, Michele Lovallo, Weiguo Song, Hui Zhang, and Luciano Telesca. 2022. "Multifractal Analysis of MODIS Aqua and Terra Satellite Time Series of Normalized Difference Vegetation Index and Enhanced Vegetation Index of Sites Affected by Wildfires" Entropy 24, no. 12: 1748. https://doi.org/10.3390/e24121748
APA StyleBa, R., Lovallo, M., Song, W., Zhang, H., & Telesca, L. (2022). Multifractal Analysis of MODIS Aqua and Terra Satellite Time Series of Normalized Difference Vegetation Index and Enhanced Vegetation Index of Sites Affected by Wildfires. Entropy, 24(12), 1748. https://doi.org/10.3390/e24121748







