Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback
Abstract
1. Introduction
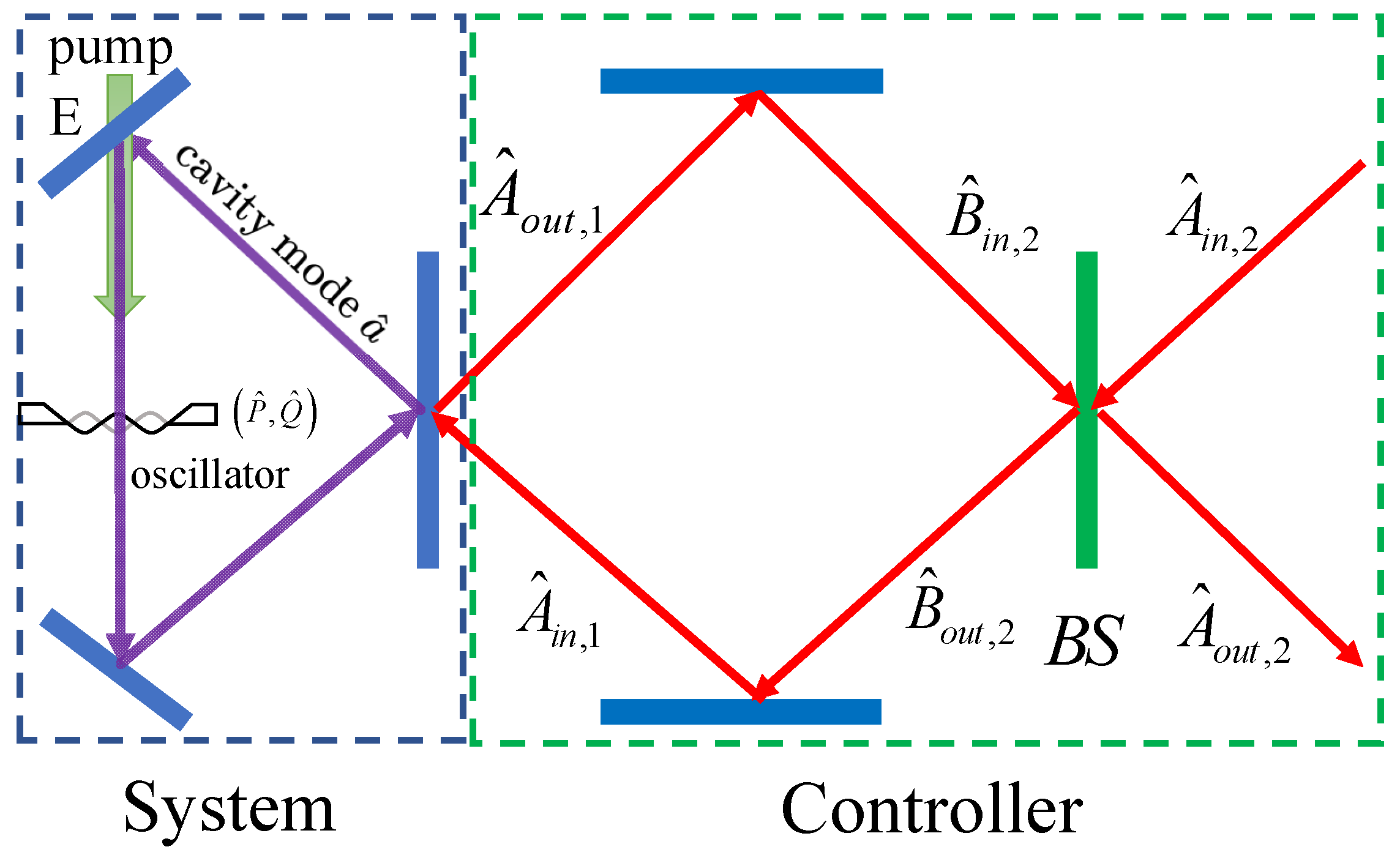
2. Cavity Optomechanical System Assisted by the Coherent Feedback
3. Derivation of Squeezing Spectrum
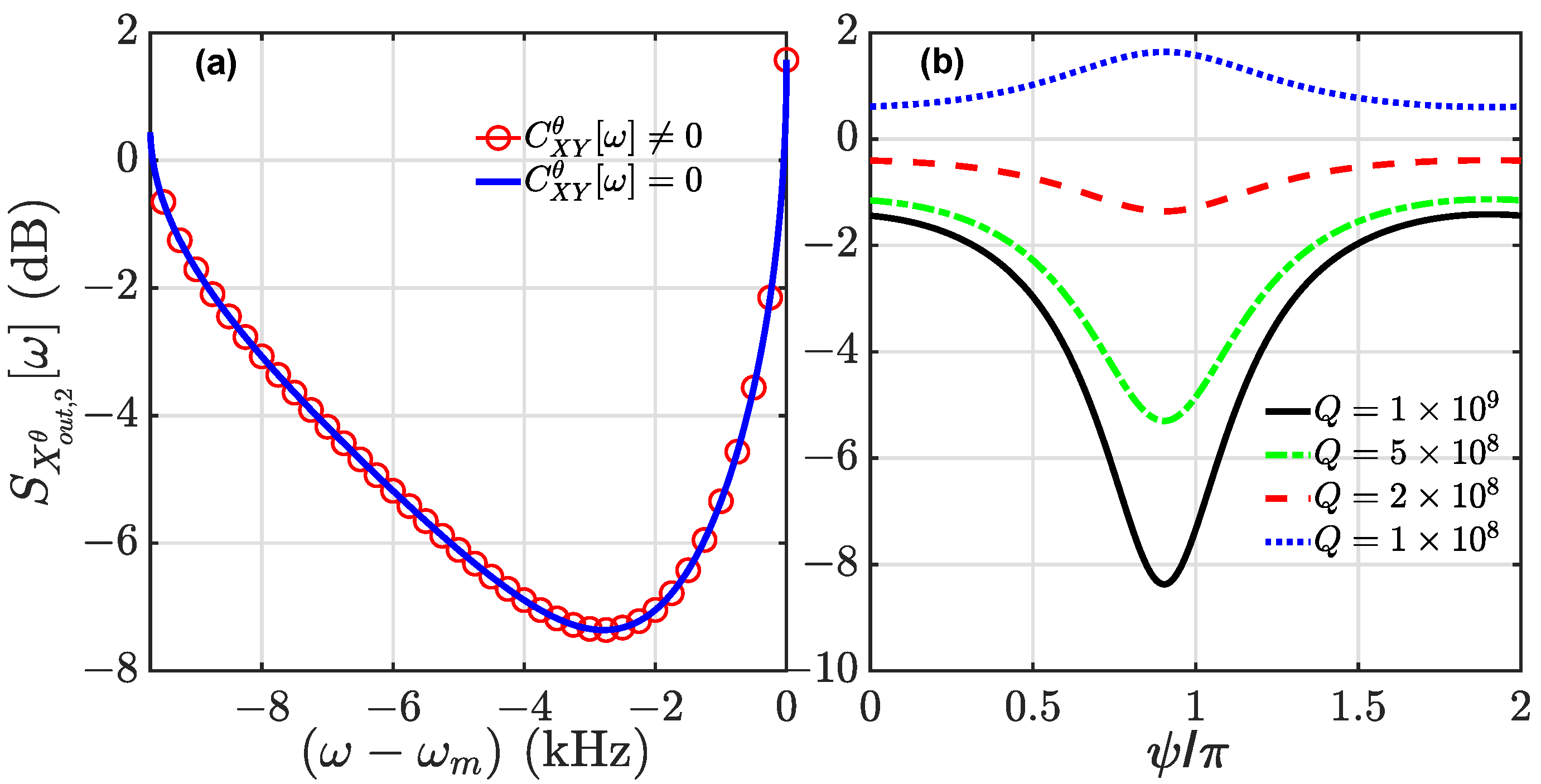
Enhancement of Squeezing with the Optimal Coherent Feedback
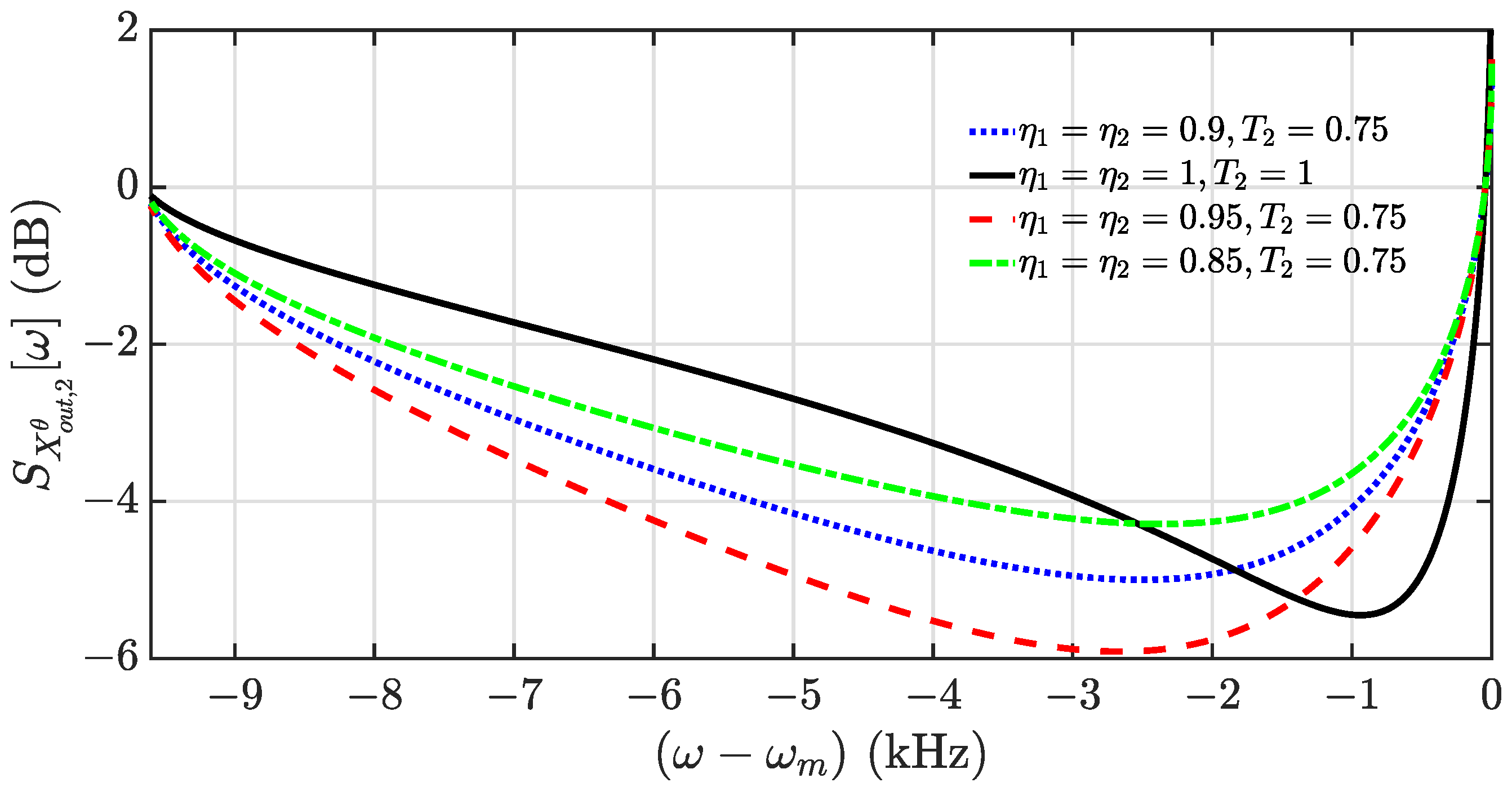
4. Effects of Optical and Mechanical Losses on Optical Squeezing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Jaekel, M.T.; Reynaud, S. Quantum limits in interferometric measurements. Europhys. Lett. 1990, 13, 301. [Google Scholar] [CrossRef]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef]
- Usenko, V.C.; Filip, R. Squeezed-state quantum key distribution upon imperfect reconciliation. New J. Phys. 2011, 13, 113007. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; Garcia-Patrón, P.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Menicucci, N.C. Fault-tolerant measurement-based quantum computing with continuous-variable cluster states. Phys. Rev. Lett. 2014, 112, 120504. [Google Scholar] [CrossRef]
- Taylor, M.A.; Janousek, J.; Daria, V.; Knittel, J.; Hage, B.; Bachor, H.A.; Bowen, W.P. Biological measurement beyond the quantum limit. Nature Photon 2013, 7, 229–233. [Google Scholar] [CrossRef]
- Li, B.B.; Bílek, J.; Hoff, U.B.; Madsen, L.S.; Forstner, S.; Prakash, V.; Schäfermeier, C.; Gehring, T.; Bowen, W.P.; Andersen, U.L. Quantum enhanced optomechanical magnetometry. Optica 2018, 5, 850–856. [Google Scholar] [CrossRef]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 1985, 55, 2409. [Google Scholar] [CrossRef]
- Shelby, R.M.; Levenson, M.D.; Perlmutter, S.H.; DeVoe, R.G.; Walls, D.F. Broad-band parametric deamplification of quantum noise in an optical fiber. Phys. Rev. Lett. 1986, 57, 691. [Google Scholar] [CrossRef]
- Wu, L.A.; Kimble, H.J.; Hall, J.L.; Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 1986, 57, 2520. [Google Scholar] [CrossRef] [PubMed]
- Vahlbruch, H.; Mehmet, M.; Chelkowski, S.; Hage, B.; Franzen, A.; Lastzka, N.; Goßler, S.; Danzmann, K.; Schnabel, R. Observation of squeezed light with 10-dB quantum noise reduction. Phys. Rev. Lett. 2008, 100, 033602. [Google Scholar] [CrossRef] [PubMed]
- Eberle, T.; Steinlechner, S.; Bauchrowitz, J.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. Quantum enchancement of the zero-area sagnac interferometer topology for gravitational wave detection. Phys. Rev. Lett. 2010, 104, 251102. [Google Scholar] [CrossRef]
- Mehmet, M.; Ast, S.; Eberle, T.; Steinlechner, S.; Vahlbruch, H.; Schnabel, R. Squeezed light at 1550 nm with a quantum noise reduction of 12.3 dB. Opt. Express 2011, 19, 25763. [Google Scholar] [CrossRef] [PubMed]
- Vahlbruch, H.; Mehmet, M.; Danzmann, K.; Schnabel, R. Detection of 15 dB squeezed states of light and their application for the absolute calibration of photonelectric quantum efficiency. Phys. Rev. Lett. 2016, 117, 110801. [Google Scholar] [CrossRef] [PubMed]
- Purdy, T.P.; Peterson, R.W.; Regal, C.A. Observation of radiation pressure shot noise on a macroscopic object. Science 2013, 339, 801. [Google Scholar] [CrossRef]
- Fabre, C.; Pinard, M.; Bourzeix, S.; Heidmann, A.; Giacobino, E.; Reynaud, S. Quantum-noise reduction using a cavity with a movable mirror. Phys. Rev. A 1994, 49, 1337. [Google Scholar] [CrossRef]
- Mancini, S.; Tombesi, P. Quantum noise reduction by radiation pressure. Phys. Rev. A 1994, 49, 4055. [Google Scholar] [CrossRef]
- Ockeloen-Korppi, C.F.; Damskägg, E.; Pirkkalainen, J.M.; Heikkilä, T.T.; Massel, F.; Sillanpää, M.A. Noiseless quantum measurement and squeezing of microwave fields ultilizing mechanical vibrations. Phys. Rev. Lett. 2017, 118, 103601. [Google Scholar] [CrossRef]
- Luo, J.W.; Wu, D.W.; Miao, Q.; Wei, T.L. Research progress in non-classical microwave states preparation based on cavity optomechanical system. Acta Phys. Sin. 2020, 69, 054203. [Google Scholar] [CrossRef]
- Corbitt, T.; Chen, Y.; Khalili, F.; Ottaway, D.; Vyatchanin, S.; Whitcomb, S.; Mavalvala, N. Squeezed-state source using radiation-pressure-induced rigidity. Phys. Rev. A 2006, 73, 023801. [Google Scholar] [CrossRef]
- Aggarwal, N.; Cullen, T.J.; Cripe, J.; Cole, G.D.; Lanza, R.; Libson, A.; Follman, D.; Heu, P.; Corbitt, T.; Mavalvala, N. Room-temperature optomechanical suqeezing. Nat. Phys. 2020, 16, 784–788. [Google Scholar] [CrossRef]
- Xuereb, A. Squeezing hots up. Nat. Phys. 2020, 16, 710–711. [Google Scholar] [CrossRef]
- Mehmet, M.; Vahlbruch, H.; Lastzka, N.; Danzmann, K.; Schnabel, R. Observation of squeezed states with strong photon-number oscillations. Phys. Rev. A 2010, 81, 013814. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, C.; Gao, F.; Xiao, M. Phase-sensitive manipulations of a squeezed vacuum field in an optical parametric amplifier inside an optical cavity. Phys. Rev. Lett. 2008, 101, 233602. [Google Scholar] [CrossRef]
- Yan, Z.; Jia, X.; Su, X.; Duan, Z.; Xie, C.; Peng, K. Cascaded entanglement enhancement. Phys. Rev. A 2012, 85, 040305(R). [Google Scholar] [CrossRef]
- Xiong, B.; Li, X.; Chao, S.L.; Zhou, L. Optomechanical quadrature squeezing in the non-Markovian regime. Opt. Lett. 2018, 43, 6053–6056. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Wang, Y.P.; Yu, Y.F.; Zhang, Z.M. Quantum squeezing in a modulated optomechanical system. Opt. Express 2018, 26, 11915–11927. [Google Scholar] [CrossRef]
- Xiong, B.; Chao, S.; Shan, C.; Liu, J. Optomechanical squeezing with pulse modulation. Opt. Lett. 2022, 47, 5545–5548. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, T.; Han, X.; Zhang, S.; Wang, H.F. Mechanical squeezing induced by Duffing nonlinearity and two driving tones in an optomechanical system. Phys. Lett. A 2022, 424, 127824. [Google Scholar] [CrossRef]
- Banerjee, P.; Kalita, S.; Sarma, A.K. Mechanical Squeezing in Quadratically-coupled Optomechanical Systems. arXiv 2022, arXiv:2210.00510. [Google Scholar]
- Brooks, D.W.C.; Botter, T.; Schreppler, S.; Purdy, T.P.; Brahms, N.; Stamper-Kurn, D.M. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature 2012, 488, 476–480. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naeini, A.H.; Gröblacher, S.; Hill, J.T.; Chan, J.; Aspelmeyer, M.; Painter, O. Squeezed light from a silicon micromechanical resonator. Nature 2013, 500, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Purdy, T.P.; Yu, P.L.; Peterson, R.W.; Kampel, N.S.; Regal, C.A. Strong optomechanical squeezing of light. Phys. Rev. X 2013, 3, 031012. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Yi, Z.; Yan, Y.; Gu, W.J. Squeezed light generation in cascaded optomechanical systems. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 075403. [Google Scholar] [CrossRef]
- Lloyd, S. Coherent quantum feedback. Phys. Rev. A 2000, 62, 022108. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gough, J.E.; Wildfeuer, S. Enhancement of field squeezing using coherent feedback. Phys. Rev. A 2009, 80, 042107. [Google Scholar] [CrossRef]
- Gough, J.E.; James, M.R. The series product and its application to quantum feedforward and feedback networks. IEEE Trans. Autom. Control 2009, 54, 2530–2544. [Google Scholar] [CrossRef]
- Gough, J.E.; James, M.R.; Nurdin, H.I. Squeezing components in linear quantum feedback networks. Phys. Rev. A 2010, 81, 023804. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Milburn, G.J. All-optical versus electro-optical quantum-limited feedback. Phys. Rev. A 1994, 49, 4110. [Google Scholar] [CrossRef]
- Yanagisawa, M.; Kimura, H. Transfer function approach to quantum control— Part I: Dynamics of quantum feedback systems. IEEE Trans. Autom. Control 2003, 48, 2107–2120. [Google Scholar] [CrossRef]
- Yanagisawa, M.; Kimura, H. Transfer function approach toquantum control—Part II: Control concepts and applications. IEEE Trans. Autom. Control 2003, 48, 2121–2132. [Google Scholar] [CrossRef]
- Tsang, M.; Caves, C.M. Coherent quantum-noise cancellation for optomechanical sensors. Phys. Rev. Lett. 2010, 105, 123601. [Google Scholar] [CrossRef]
- Yamamoto, N. Coherent versus measurement feedback: Linear systems theory for quantum information. Phys. Rev. X 2014, 4, 041029. [Google Scholar] [CrossRef]
- Harwood, A.; Brunelli, M.; Serafini, A. Cavity optomechanics assisted by optical coherent feedback. Phys. Rev. A 2021, 103, 023509. [Google Scholar] [CrossRef]
- Meers, B.J. Becycling in laser-interferometric gravitational-wave detectors. Phys. Rev. D 1988, 38, 2317. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Chelkowski, S.; Hage, B.; Franzen, A.; Danzmann, K.; Schnabel, R. Demonstration of a squeezed-light-enhanced power- and signal-recycled Michelson interferometer. Phys. Rev. Lett. 2005, 95, 211102. [Google Scholar] [CrossRef]
- Mason, D.; Chen, J.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745–749. [Google Scholar] [CrossRef]
- Tsaturyan, Y.; Barg, A.; Polzik, E.S.; Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 2017, 12, 776–783. [Google Scholar] [CrossRef]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 2018, 563, 53–58. [Google Scholar] [CrossRef]
- Takeno, Y.; Yukawa, M.; Yonezawa, H.; Furusawa, A. Observation of −9 dB quadrature squeezing with improvement of phase stability in homodyne measurement. Opt. Express 2007, 15, 4321. [Google Scholar] [CrossRef]
- Iida, S.; Yukawa, M.; Yonezawa, H.; Yamamoto, N.; Furusawa, A. Experimental demonstration of coherent feedback control on optical field squeezing. IEEE Trans. Autom. Control 2012, 57, 2045–2050. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Yi, Z.; Gu, W.; Sun, L.; Ficek, Z. Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback. Entropy 2022, 24, 1741. https://doi.org/10.3390/e24121741
Wu Z, Yi Z, Gu W, Sun L, Ficek Z. Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback. Entropy. 2022; 24(12):1741. https://doi.org/10.3390/e24121741
Chicago/Turabian StyleWu, Zhenhua, Zhen Yi, Wenju Gu, Lihui Sun, and Zbigniew Ficek. 2022. "Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback" Entropy 24, no. 12: 1741. https://doi.org/10.3390/e24121741
APA StyleWu, Z., Yi, Z., Gu, W., Sun, L., & Ficek, Z. (2022). Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback. Entropy, 24(12), 1741. https://doi.org/10.3390/e24121741






