Non-Kolmogorovian Probabilities and Quantum Technologies
Abstract
1. Introduction
2. The Ideas behind Quantum Probability
2.1. In the Beginning, There Was Ontological Probabilities
“I should like only to say this: the determinism of classical physics turns out to be an illusion, created by overrating logical-mathematical concepts. It is an idol, not an ideal in scientific research and cannot, therefore, be used as an objection to the essentially indeterministic statistical interpretation of quantum mechanics.”
“It is no longer the objective events but rather the probabilities for the occurrence of certain events that can be stated in mathematical formulae. It is no longer the actual happening itself but rather the possibility of its happening—the potential, to employ a concept from Aristotle’s philosophy—that is subject to strict natural laws.”
He continues with a stronger assertion:“It was quantum mechanics that first assumed the existence of primary probabilities in the laws of nature, which could not be reduced, by means of auxiliary hypotheses, to deterministic laws, as is possible, for instance, with the thermodynamical probabilities of classical physics. This revolutionary development is considered as final by the large majority of modern physicists, first of all by Born, Heisenberg, and Bohr, with whom I myself agree.”([26], page 46)
“The state of a system (object) being given, only statistical predictions can in general be made about the results of future observations (primary probability), whereas the result of the single observation is not determined by laws, being thus an ultimate fact without cause. This is necessary in order that quantum mechanics may be regarded as the rational generalization of classical physics, and complementarity as the generalization of causality in the narrower sense.”([26], page 46, our emphasis)
“In throwing dice we do not know the fine details of the motion of our hands which determine the fall of the dice and therefore we say that the probability for throwing a special number is just one in six. The probability wave of Bohr, Kramers, Slater, however, meant more than that; it meant a tendency for something. It was a quantitative version of the old concept of “potentia” in Aristotelian philosophy. It introduced something standing in the middle between the idea of an event and the actual event, a strange kind of physical reality just in the middle between possibility and reality.”
2.2. Experimental Evidence Supports the Ontological Probabilities Assumption
2.3. How to Avoid Empirical Evidence and Return to an Ignorance Interpretation of Probabilities?
3. The Main Features of Quantum Probability
3.1. Kolmogorov’s Axioms
- (1)
- (2)
- For any denumerable family of pairwise disjoint sets
3.2. Quantum Contexts and Quantum States
- One can perform different experiments on a quantum system (trivial).
- Some of these experiments can be jointly performed. Others cannot (this is a non-trivial quantum feature).
- There is a joint probability distribution (that obeys Kolmogorov’s axioms) for experiments that can be jointly performed. However, the physics changes radically from context to context (consider the wave-particle behavior in a Mach–Zehnder interferometer): the strong dependence on the context is an expression of what can be called Bohr contextuality [57].
- There is no joint (Kolmogorovian) probability distribution for all possible contexts. This is a mathematical expression of the notion of contextuality.
- Experiments with the same content appear as repeated in different (incompatible) contexts (for quantum models of dimensions greater or equal to 3). This happens with a high degree of regularity, and can be given a very precise mathematical description. This is a highly non-trivial feature of quantum physics, which has no classical analog; a sort of “identification principle” seems to be at work here. As a result, empirical contexts are “intertwined” in a complex way. The characterization of this intertwining is one of the main challenges for understanding quantum contextuality.
- The marginal probabilities associated with concrete experiments do not depend on the other experiments that can be jointly performed. This is a highly non-trivial feature of quantum theory and is known as the no-signal condition.
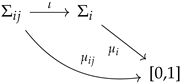
- For each in Table 1, we have a probability space .
- For each row i of the matrix, we have a joint probability space .
- and have the same content, but they should not be a priori identified (and a similar conclusion holds for the rest of the repeated random variables).

- (1)
- (2)
- For any denumerable family of pairwise orthogonal projections


3.3. Negative Probabilities
- Alternative 1: paste the Boolean algebra and end up with a non-Boolean structure as we did in the previous section (and define the states as usual in the quantum logical approaches).
- Alternative 2: keep using Boolean algebras, but with negative probabilities.

4. Quantum Information Theory and Quantum Technologies: A Non-Kolmogorovian Perspective
4.1. What Is a Computer?
4.2. Deterministic Classical Computing
4.3. Probabilistic Classical Computing
4.4. Quantum Computing in a Schematic Way
- Step 1
- We initialize the computer in the state (or any other conveniently chosen state).
- Step 2
- Next, we apply a collection of gates represented by unitary operators , and obtain a final state .
- Step 3
- We perform measurements on a selected set of qubits. Depending on the results obtained, we decide which other steps to follow.
- Step 1’
- We initialize the computer in the state (or any other conveniently chosen state).
- Step 1’
- Next, we apply a collection of gates. Real quantum gates are only approximately unitary. Thus, a final non-pure state is obtained.
- Step 1’
- We perform measurements on a selected set of qubits. Depending on the result obtained, we decide which other steps to follow. Measurements (readouts) are also noisy (and this has to be considered too).
- Step 1. Start with an initial reference state .
- Step 2. Apply a collection of automorphisms to reach a desired final state .
- Step 3. Measure the system when state is reached, check the result obtained; depending on the result, stop the process or continue with the the other steps of the algorithm.
5. The Extended Church–Turing Thesis and Quantum Supremacy
The ECTT can be interpreted as follows: every physical evolution can be efficiently modeled using a classical computer. R. P. Feynman was one of the first people who conjectured that there could be quantum systems for which time evolution could not be modeled efficiently using classical computers. Nowadays, we have good reasons to believe that this conjecture is true and that the ECTT is false. Quantum computers seem to outperform their classical cousins. Recent experiments support this idea [5,6,7,8,9]. Related to the failure of the ECTT, we must mention quantum supremacy. It can be defined as follows:All computational problems that are efficiently solvable by realistic physical devices are efficiently solvable by a probabilistic Turing machine.
5.1. Quantum Random Circuits and Cross-Entropy Benchmarking
One may wonder to what extent algorithmic innovation can enhance classical simulations. Our assumption, based on insights from complexity theory, is that the cost of this algorithmic task is exponential in circuit size. Indeed, simulation methods have improved steadily over the past few years. We expect that lower simulation costs than reported here will eventually be achieved, but we also expect that they will be consistently outpaced by hardware improvements on larger quantum processors.
5.2. Why Is There a Quantum Speed-Up?
- Preparation of qubits in all possible computational basis states;
- All possible Clifford gates (Hadamard, controlled-NOT, and phase gate S); and
- Performing measurements in the computational basis.
- The power of quantum computers seems to rely on their capability of generating a large part of the richness of the quantum state space. Due to the Gottesman–Knill theorem, it is not enough to generate superposed and entangled states. Universal quantum computers need to generate a rich enough subset of the quantum state space.
- Generating the quantum state space is equivalent to realizing all possible rotations implemented by unitary operators (quantum gates) in a coherent way. For this task, a universal set of gates is needed.
- (Quantum) contextuality is directly related to the non-Kolmogorovian nature of the quantum probability calculus.
Quantum systems are the only sources of a true non-Kolmogorovian probability known to us. It is exponentially hard for a classical entity to efficiently simulate a sufficiently rich non-Kolmogorovian probability space. Therefore, quantum advantage can be defined as the ability of a quantum device in generating genuine quantum contextuality, which is directly related to its ability in exploring the quantum probability space by the application of a rich enough set of quantum gates.
6. Conclusions
- The probabilistic characteristics of quantum phenomena seem to have an ontological nature (this is the main working hypothesis underlying quantum theory). All empirical evidence to date supports this assumption, and it lies at the basis of the development of technologies that rely on genuine randomness.
- As such, the ontological probabilities involved in quantum phenomena are described by a highly non-classical probabilistic calculus. Quantum systems are, to our knowledge, the only examples of entities obeying those very precise mathematical laws. Therefore, quantum systems are the only genuine sources of a non-Kolmogorovian probability.
- Quantum information theory possibly emerges from the assumption that the devices used to store, process, and transmit information are entities obeying a genuine (not simulated) non-Kolmogorovian probability calculus.
- Quantum computing can be considered a non-Kolmogorovian version of classical probabilistic computing. From this perspective, the orthomodular lattice formed by the projection operators of the Hilbert space is an essential algebraic structure for understanding quantum advantage and quantum contextuality (see also [87]).
- The degree to which a quantum device is able to generate a non-classical probability space can be quantified by appealing to measures, such as the cross-entropy benchmarking (used in recent experiments attempting to demonstrate quantum advantage).
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Riedel, M.F.; Binosi, D.; Thew, R.; Calarco, T. The European quantum technologies flagship programme. Quantum Sci. Technol. 2017, 2, 030501. [Google Scholar] [CrossRef]
- Hinds, E.; Blatt, R. Manipulating individual quantum systems. Nature 2012, 492, 55. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.W.; Kurz, C.; Hume, D.B.; Plessow, P.N.; Leibrandt, D.R.; Leibfried, D. Preparation and coherent manipulation of pure quantum states of a single molecular ion. Nature 2017, 545, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Bova, F.; Goldfarb, A.; Melko, R.G. Commercial applications of quantum computing. EPJ Quantum Technol. 2021, 8, 2. [Google Scholar] [CrossRef] [PubMed]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.-S.; Wang, H.; Deng, Y.-H.; Chen, M.-C.; Peng, L.-C.; Luo, Y.-H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Zhong, H.-S.; Deng, Y.-H.; Qin, J.; Wang, H.; Chen, M.-C.; Peng, L.-C.; Luo, Y.-H.; Wu, D.; Gong, S.-Q.; Su, H.; et al. Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light. Phys. Rev. Lett. 2021, 127, 180502. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.-S.; Cao, S.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef]
- Holik, F.; Bosyk, G.M. Classical Models for Quantum Information. In What is Quantum Information? Lombardi, O., Fortin, S., Holik, F., López, C., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 207–230. [Google Scholar] [CrossRef]
- Holik, F.; Bosyk, G.M.; Bellomo, G. Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory. Entropy 2015, 17, 7349–7373. [Google Scholar] [CrossRef]
- Holik, F.; Sergioli, G.; Freytes, H.; Plastino, A. Logical Structures Underlying Quantum Computing. Entropy 2019, 21, 77. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, O.; Fortin, S.; Holik, F.; López, C.e. What is Quantum Information? Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Lombardi, O.; Holik, F.; Vanni, L. What is quantum information? Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2016, 56, 17–26. [Google Scholar] [CrossRef]
- Timpson, C. Quantum Information Theory and the Foundations of Quantum Mechanics. Ph.D. Thesis, University of Oxford, Oxford, UK, 2004. [Google Scholar]
- Cuffaro, M.E. The Philosophy of Quantum Computing. In Quantum Computing in the Arts and Humanities: An Introduction to Core Concepts, Theory and Applications; Miranda, E.R., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 107–152. [Google Scholar] [CrossRef]
- Cuffaro, M.E. On the Significance of the Gottesman-Knill Theorem. Br. J. Philos. Sci. 2017, 68, 91–121. [Google Scholar] [CrossRef][Green Version]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Bera, M.N.; Acín, A.; Kuś, M.; Mitchell, M.W.; Lewenstein, M. Randomness in quantum mechanics: Philosophy, physics and technology. Rep. Prog. Phys. 2017, 80, 124001. [Google Scholar] [CrossRef]
- Agresti, I.; Poderini, D.; Guerini, L.; Mancusi, M.; Carvacho, G.; Aolita, L.; Cavalcanti, D.; Chaves, R.; Sciarrino, F. Experimental device-independent certified randomness generation with an instrumental causal structure. Commun. Phys. 2020, 3, 110. [Google Scholar] [CrossRef]
- Petrov, M.; Radchenko, I.; Steiger, D.; Renner, R.; Troyer, M.; Makarov, V. Independent quality assessment of a commercial quantum random number generator. EPJ Quantum Technol. 2022, 9, 17. [Google Scholar] [CrossRef]
- Gallego, R.; Masanes, L.; De La Torre, G.; Dhara, C.; Aolita, L.; Acín, A. Full randomness from arbitrarily deterministic events. Nat. Commun. 2013, 4, 2654. [Google Scholar] [CrossRef]
- Calude, C.S.; Dinneen, M.J.; Dumitrescu, M.; Svozil, K. How Random Is Quantum Randomness? An Experimental Approach. arXiv 2009, arXiv:0912.4379. [Google Scholar]
- Born, M. Nobel lecture. In Published in “Les Prix Nobel”. Stockholm: Nobel Foundation; The Nobel Foundation: Stockholm, Sweden, 1954. [Google Scholar]
- Heisenberg, W. Across the Frontiers; Harper & Row: New York, NY, USA, 1974. [Google Scholar]
- Pauli, W. Writings on Physics and Philosophy; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Heisenberg, W. Physics and Philosophy; Great Books of the Western World; Springer: Berlin/Heidelberg, Germany, 1994; Volume 56. [Google Scholar]
- Younan, A. If a Photon Falls in the Woods: An Aristotelian Answer to a Quantum Question. Heythrop J. 2022, 63, 458–472. [Google Scholar] [CrossRef]
- Jaeger, G. Quantum potentiality revisited. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160390. [Google Scholar] [CrossRef] [PubMed]
- Kastner, R.E.; Kauffman, S.; Epperson, M. Taking Heisenberg’s Potentia Seriously. Int. J. Quantum Found. 2018, 4, 158–172. [Google Scholar]
- Silva, I. Werner Heisenberg and Thomas Aquinas on Natural Indeterminism. New Blackfriars 2013, 94, 635–653. [Google Scholar] [CrossRef]
- Ronde, C.D. Immanent Powers Versus Causal Powers (Propensities, Latencies and Dispositions) in Quantum Mechanics. In Probing the Meaning of Quantum Mechanics; World Scientific: Singapore, 2019; pp. 121–157. [Google Scholar] [CrossRef]
- Popper, K. Quantum Theory and the Schism in Physics: From the Postscript to the Logic of Scientific Discovery; Routledge: London, UK, 1982. [Google Scholar]
- Maxwell, N. Quantum Propensiton Theory: A Testable Resolution of the Wave/Particle Dilemma. Br. J. Philos. Sci. 1988, 39, 1–50. [Google Scholar] [CrossRef]
- da Costa, N.; Lombardi, O.; Lastiri, M. A modal ontology of properties for quantum mechanics. Synthese 2013, 190, 3671–3693. [Google Scholar] [CrossRef]
- Holik, F.; Jorge, J.P.; Krause, D.; Lombardi, O. Quasi-set theory: A formal approach to a quantum ontology of properties. Synthese 2022, 200, 401. [Google Scholar] [CrossRef]
- Zeilinger, A. The message of the quantum. Nature 2005, 438, 743. [Google Scholar] [CrossRef]
- Hnilo, A. Non-Boolean Hidden Variables model reproduces Quantum Mechanics’ predictions for Bell’s experiment. arXiv 2020, arXiv:2005.10367. [Google Scholar]
- Khrennikov, A.; Alodjants, A. Classical (Local and Contextual) Probability Model for Bohm-Bell Type Experiments: No-Signaling as Independence of Random Variables. Entropy 2019, 21, 157. [Google Scholar] [CrossRef]
- Maudlin, T. What Bell did. J. Phys. A Math. Theor. 2014, 47, 424010. [Google Scholar] [CrossRef]
- Werner, R.F. Comment on ‘What Bell did’. J. Phys. A Math. Theor. 2014, 47, 424011. [Google Scholar] [CrossRef]
- Maudlin, T. Reply to Comment on ‘What Bell did’. J. Phys. A Math. Theor. 2014, 47, 424012. [Google Scholar] [CrossRef][Green Version]
- Werner, R.F. What Maudlin replied to. arXiv 2014, arXiv:1411.2120. [Google Scholar]
- Sánchez, C.M.; Chattah, A.K.; Wei, K.X.; Buljubasich, L.; Cappellaro, P.; Pastawski, H.M. Perturbation Independent Decay of the Loschmidt Echo in a Many-Body System. Phys. Rev. Lett. 2020, 124, 030601. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, C.M.; Chattah, A.K.; Pastawski, H.M. Emergent decoherence induced by quantum chaos in a many-body system: A Loschmidt echo observation through NMR. Phys. Rev. A 2022, 105, 052232. [Google Scholar] [CrossRef]
- Caticha, A. Entropic Dynamics and Quantum “Measurement”. arXiv 2022, arXiv:2208.02156. [Google Scholar]
- Zurek, W.H. Quantum theory of the classical: Quantum jumps, Born’s Rule and objective classical reality via quantum Darwinism. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20180107. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Theory of the Classical: Einselection, Envariance, Quantum Darwinism and Extantons. Entropy 2022, 24, 1520. [Google Scholar] [CrossRef]
- Holik, F.; Jorge, J.P. Open problems in the development of a quantum mereology and their ontological implications. 2022; under review. [Google Scholar] [CrossRef]
- Felline, L. The Measurement Problem and Two Dogmas About Quantum Mechanics. In Quantum, Probability, Logic: The Work and Influence of Itamar Pitowsky; Hemmo, M., Shenker, O., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 285–304. [Google Scholar] [CrossRef]
- Janas, M.; Michael, E.; Cuffaro, M.J. Quantum Mechanics on an Informational Approach: Structure and Interpretation; Springer: Berlin/Heidelberg, Germany, 2022; Volume 340. [Google Scholar]
- Prigogine, I. Why irreversibility? The formulation of classical and quantum mechanics for nonintegrable systems. Int. J. Quantum Chem. 1995, 53, 105–118. [Google Scholar] [CrossRef]
- Bishop, R.C. Nonequilibrium statistical mechanics Brussels-Austin style. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2004, 35, 1–30. [Google Scholar] [CrossRef]
- Gadella, M.; Fortín, S.; Jorge, J.P.; Losada, M. Mathematical Models for Unstable Quantum Systems and Gamow States. Entropy 2022, 24, 804. [Google Scholar] [CrossRef] [PubMed]
- Fortin, S.; Gadella, M.; Holik, F.; Losada, M. Gamow vectors formalism applied to the Loschmidt echo. Eur. Phys. J. Plus 2020, 135, 738. [Google Scholar] [CrossRef]
- Holik, F.; Massri, C.; Plastino, A.; Sáenz, M. Generalized Probabilities in Statistical Theories. Quantum Rep. 2021, 3, 389–416. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextuality, Complementarity, Signaling, and Bell tests. Entropy 2022, 24, 1380. [Google Scholar] [CrossRef]
- de Barros, J.A.; Holik, F.; Krause, D. Contextuality and Indistinguishability. Entropy 2017, 19, 435. [Google Scholar] [CrossRef]
- Cervantes, V.H.; Dzhafarov, E.N. Snow queen is evil and beautiful: Experimental evidence for probabilistic contextuality in human choices. Decision 2018, 5, 193–204. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kujala, J.V. Contextuality is about identity of random variables. Phys. Scr. 2014, T163, 014009. [Google Scholar] [CrossRef]
- de Barros, J.A.; Holik, F.; Krause, D. Indistinguishability and the origins of contextuality in physics. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2019, 377, 20190150. [Google Scholar] [CrossRef]
- de Barros, J.A.; Holik, F. Indistinguishability and Negative Probabilities. Entropy 2020, 22, 829. [Google Scholar] [CrossRef]
- Svozil, K. Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive. Quantum Rep. 2020, 2, 278–292. [Google Scholar] [CrossRef]
- Navara, M.; Rogalewicz, V. The pasting constructions for orthomodular posets. Math. Nachrichten 1991, 154, 157–168. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E. The Problem of Hidden Variables in Quantum Mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Cabello, A.; Estebaranz, J.M.; García-Alcaine, G. Bell-Kochen-Specker theorem: A proof with 18 vectors. Phys. Lett. A 1996, 212, 183–187. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, J.; Luan, C.Y.; Um, M.; Wang, Y.; Qiao, M.; Xie, T.; Zhang, J.N.; Cabello, A.; Kim, K. Significant loophole-free test of Kochen-Specker contextuality using two species of atomic ions. Sci. Adv. 2022, 8, eabk1660. [Google Scholar] [CrossRef]
- Budroni, C.; Cabello, A.; Gühne, O.; Kleinmann, M.; Larsson, J.Å. Kochen-Specker Contextuality. arXiv 2021, arXiv:2102.13036. [Google Scholar]
- Grangier, P.; Auffèves, A. What is quantum in quantum randomness? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170322. [Google Scholar] [CrossRef] [PubMed]
- Auffèves, A.; Grangier, P. Extracontextuality and extravalence in quantum mechanics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170311. [Google Scholar] [CrossRef]
- Kalmbach, G. Orthomodular Lattices; Academic Press: London, UK, 1983; Volume 18. [Google Scholar]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885. [Google Scholar] [CrossRef]
- Accardi, L. Quantum probability and Hilbert’s sixth problem. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2018, 376, 20180030. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextual viewpoint to quantum stochastics. J. Math. Phys. 2003, 44, 2471–2478. [Google Scholar] [CrossRef]
- Cahill, K.E.; Glauber, R.J. Density Operators and Quasiprobability Distributions. Phys. Rev. 1969, 177, 1882–1902. [Google Scholar] [CrossRef]
- Leonhardt, U. Discrete Wigner function and quantum-state tomography. Phys. Rev. A 1996, 53, 2998–3013. [Google Scholar] [CrossRef] [PubMed]
- Kenfack, A.; Życzkowski, K. Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B Quantum Semiclassical Opt. 2004, 6, 396–404. [Google Scholar] [CrossRef]
- Cormick, C.; Galvão, E.F.; Gottesman, D.; Paz, J.P.; Pittenger, A.O. Classicality in discrete Wigner functions. Phys. Rev. A 2006, 73, 012301. [Google Scholar] [CrossRef]
- Deléglise, S.; Dotsenko, I.; Sayrin, C.; Bernu, J.; Brune, M.; Raimond, J.M.; Haroche, S. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 2008, 455, 510–514. [Google Scholar] [CrossRef]
- Hillery, M.; O’Connell, R.; Scully, M.; Wigner, E. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Ferrie, C. Quasi-probability representations of quantum theory with applications to quantum information science. Rep. Prog. Phys. 2011, 74, 116001. [Google Scholar] [CrossRef]
- Manfredi, G. Logical entropy and negative probabilities in quantum mechanics. 4open 2022, 5, 8. [Google Scholar] [CrossRef]
- Renes, J.M. The Physics Of Quantum Information: Complementarity, Uncertainty, And Entanglement. Int. J. Quantum Inf. 2013, 11, 1330002. [Google Scholar] [CrossRef]
- Shahandeh, F. Quantum computational advantage implies contextuality. arXiv 2021, arXiv:2112.00024. [Google Scholar]
- Aaronson, S.; Arkhipov, A. The computational complexity of linear optics. In Proceedings of the 43rd annual ACM symposium on Theory of computing (STOC ’11), San Jose, CA, USA, 6–8 June 2011; ACM: New York, NY, USA, 2011; pp. 333–342. [Google Scholar]
- Kitaev, A.; Shen, A.; Vyalyi, M. Classical and Quantum Computation Graduate Studies in Mathematics; American Mathematical Society Providence: Providence, RI, USA, 2002; Volume 47. [Google Scholar]
- Bub, J. Quantum computaton from a quantum logical perspective. Quantum Inf. Comput. 2007, 7, 281–296. [Google Scholar] [CrossRef]
- Howard, M.; Wallman, J.; Veitch, V.; Emerson, J. Contextuality supplies the ‘magic’ for quantum computation. Nature 2014, 510, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Galvão, E.F. Discrete Wigner functions and quantum computational speedup. Phys. Rev. A 2005, 71, 042302. [Google Scholar] [CrossRef]
- Veitch, V.; Ferrie, C.; Gross, D.; Emerson, J. Negative quasi-probability as a resource for quantum computation. New J. Phys. 2012, 14, 113011. [Google Scholar] [CrossRef]
- Mari, A.; Eisert, J. Positive Wigner Functions Render Classical Simulation of Quantum Computation Efficient. Phys. Rev. Lett. 2012, 109, 230503. [Google Scholar] [CrossRef] [PubMed]
- Pednault, E.; Gunnels, J.A.; Nannicini, G.; Horesh, L.; Wisnieff, R. Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits. arXiv 2019, arXiv:1910.09534. [Google Scholar]
- Liu, Y.A.; Liu, X.L.; Li, F.N.; Fu, H.; Yang, Y.; Song, J.; Zhao, P.; Wang, Z.; Peng, D.; Chen, H.; et al. Closing the “Quantum Supremacy” Gap: Achieving Real-Time Simulation of a Random Quantum Circuit Using a New Sunway Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC ’21, St. Louis, MO, USA, 14–19 November 2021; Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Gottesman, D. The Heisenberg Representation of Quantum Computers. arXiv 1998, arXiv:quant-ph/9807006. [Google Scholar]
- Booth, R.; Chabaud, U.; Emeriau, P.E. Contextuality and Wigner negativity are equivalent for continuous-variable quantum measurements. arXiv 2021, arXiv:2111.13218v1. [Google Scholar]



| ∅ | ∅ | ||
| ∅ | ∅ | ||
| ∅ | ∅ | ||
| ∅ | ∅ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holik, F.H. Non-Kolmogorovian Probabilities and Quantum Technologies. Entropy 2022, 24, 1666. https://doi.org/10.3390/e24111666
Holik FH. Non-Kolmogorovian Probabilities and Quantum Technologies. Entropy. 2022; 24(11):1666. https://doi.org/10.3390/e24111666
Chicago/Turabian StyleHolik, Federico Hernán. 2022. "Non-Kolmogorovian Probabilities and Quantum Technologies" Entropy 24, no. 11: 1666. https://doi.org/10.3390/e24111666
APA StyleHolik, F. H. (2022). Non-Kolmogorovian Probabilities and Quantum Technologies. Entropy, 24(11), 1666. https://doi.org/10.3390/e24111666







