Mather β-Function for Ellipses and Rigidity
Abstract
1. Introduction
2. Results
3. Preliminaries and Methods
3.1. Non-Standard Generating Function
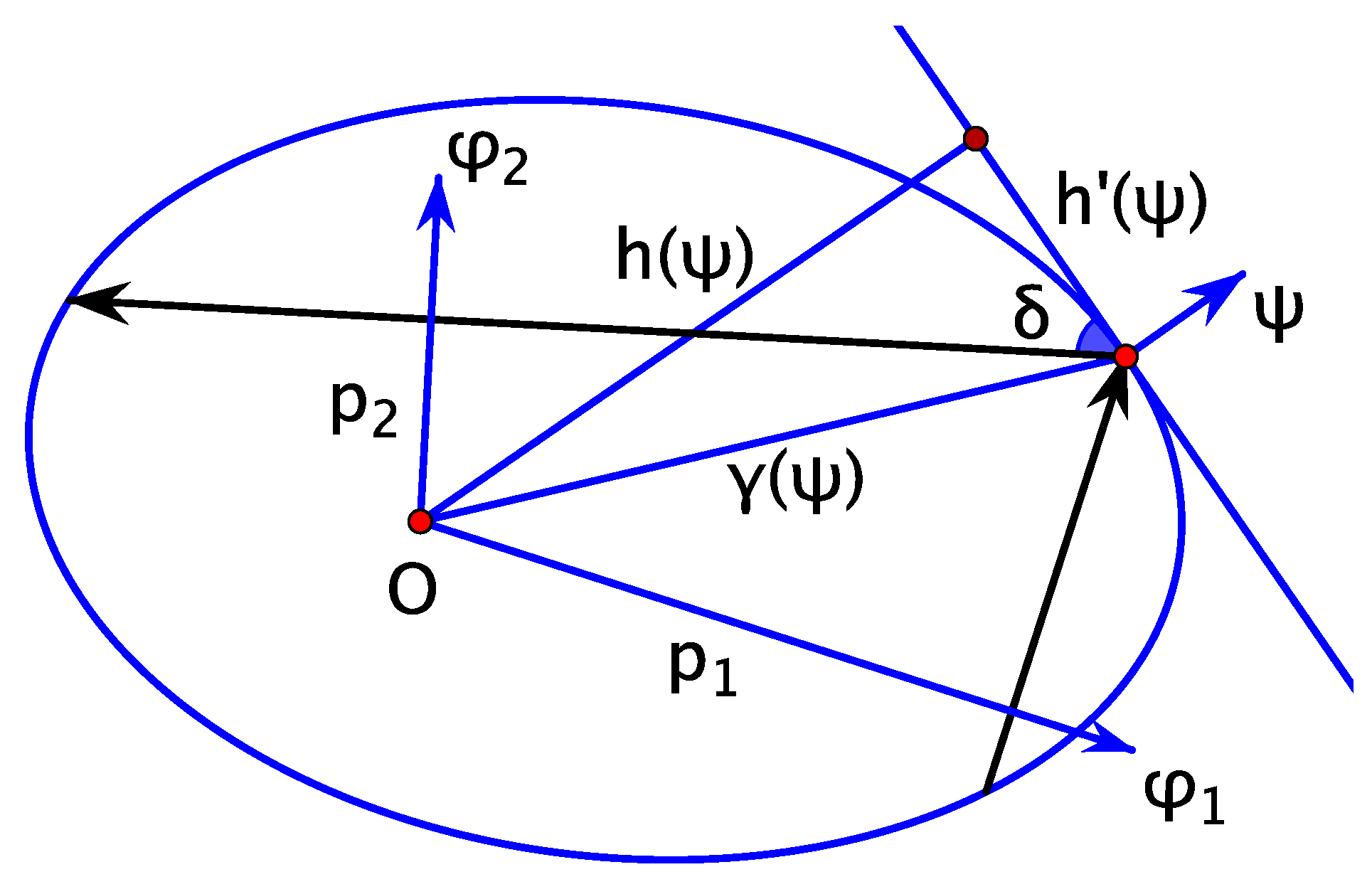
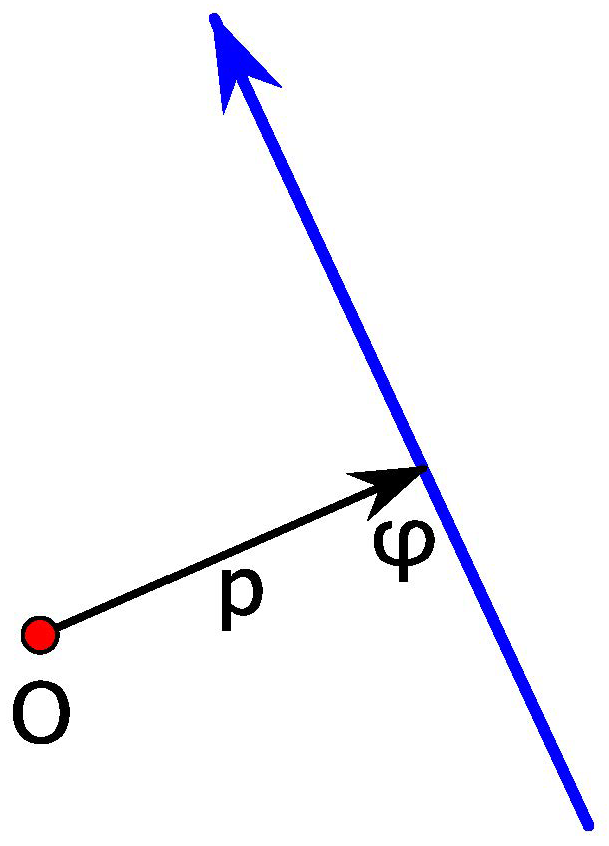
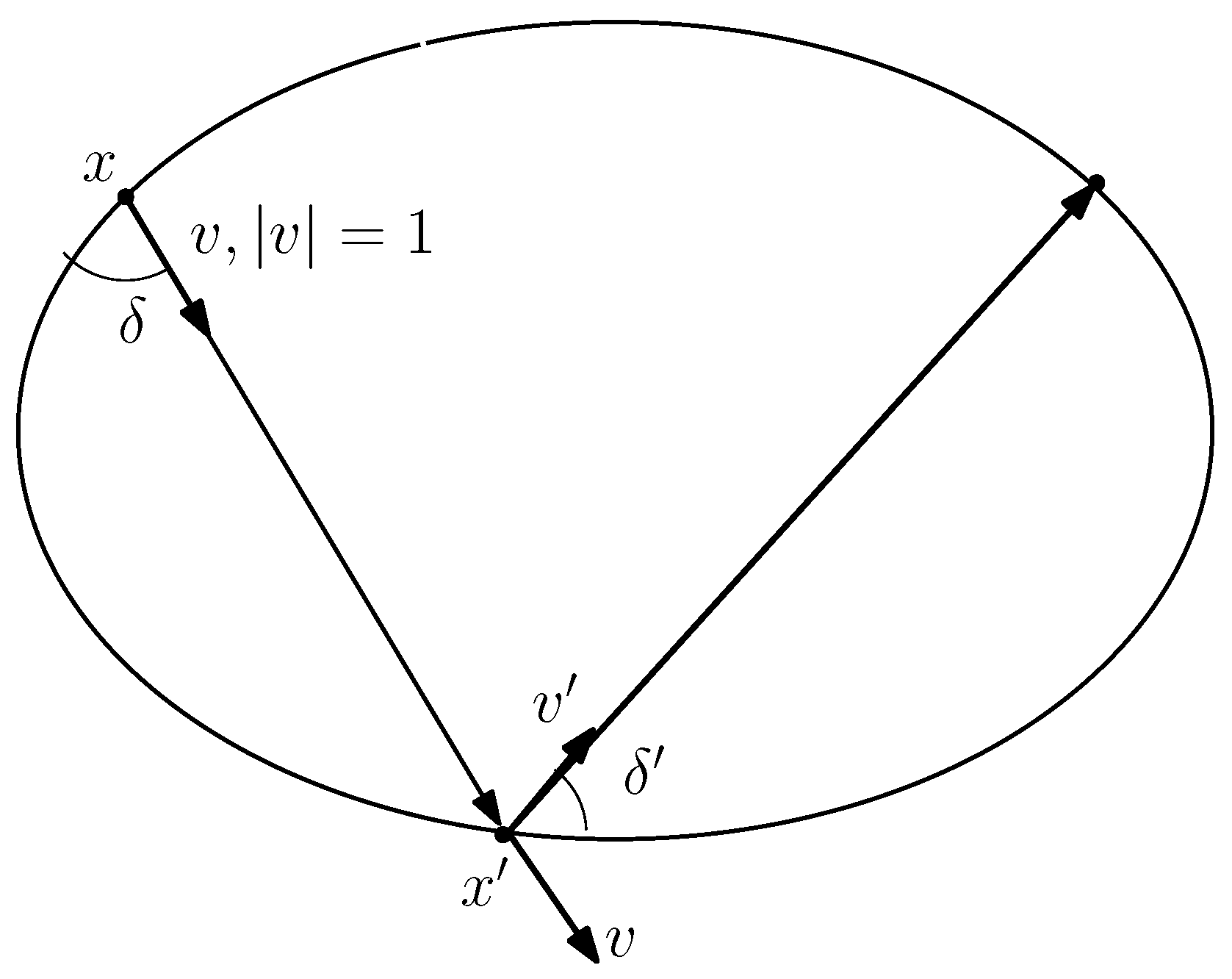
3.2. Integral for Elliptic Billiard in Various Forms
3.3. The Relations between Conserved Quantities
- 1.
- 2.
- 3.
- In terms of the eccentricities of we have the formulas:
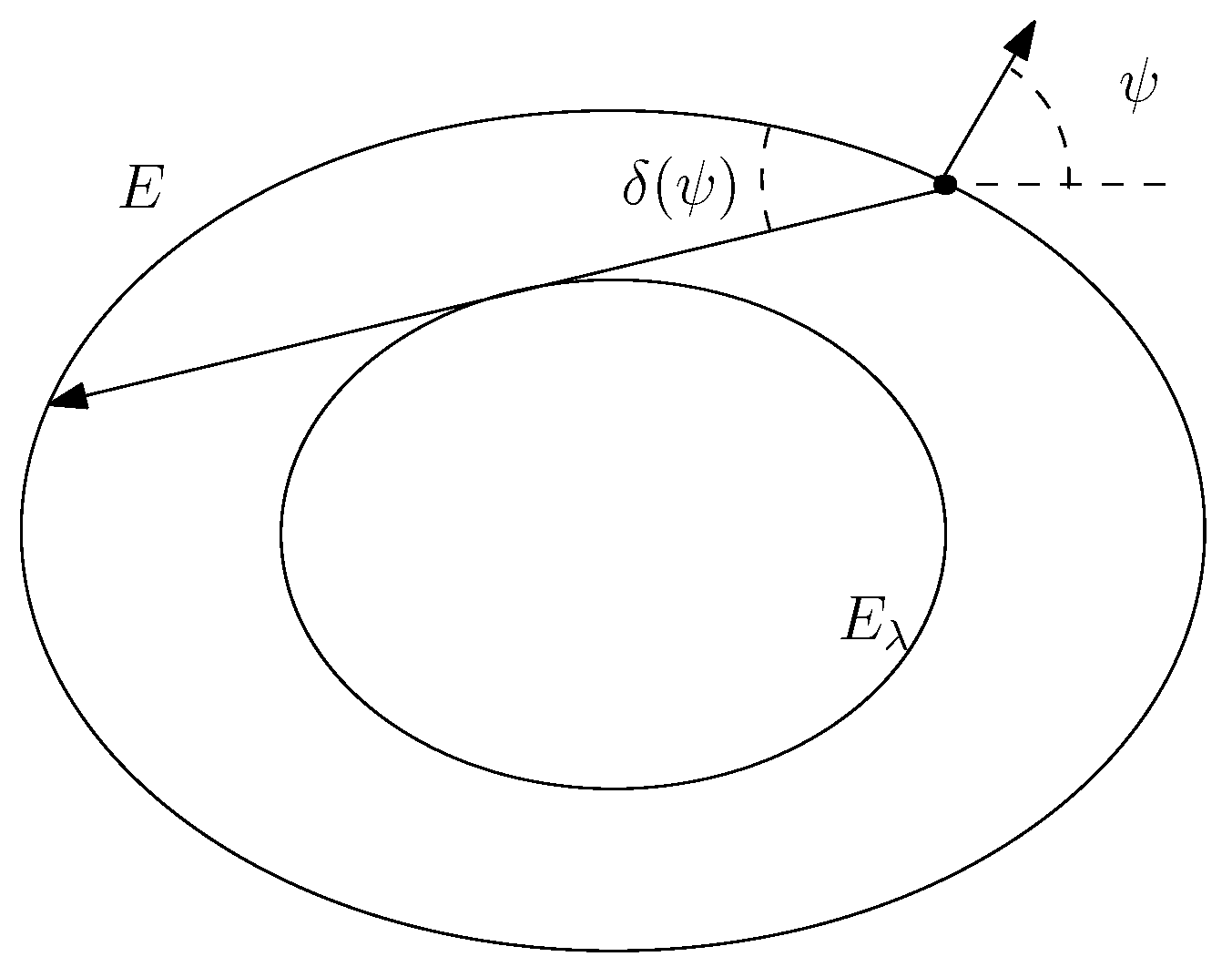
4. Invariant Measure on an Invariant Curve
5. Mather β-Function
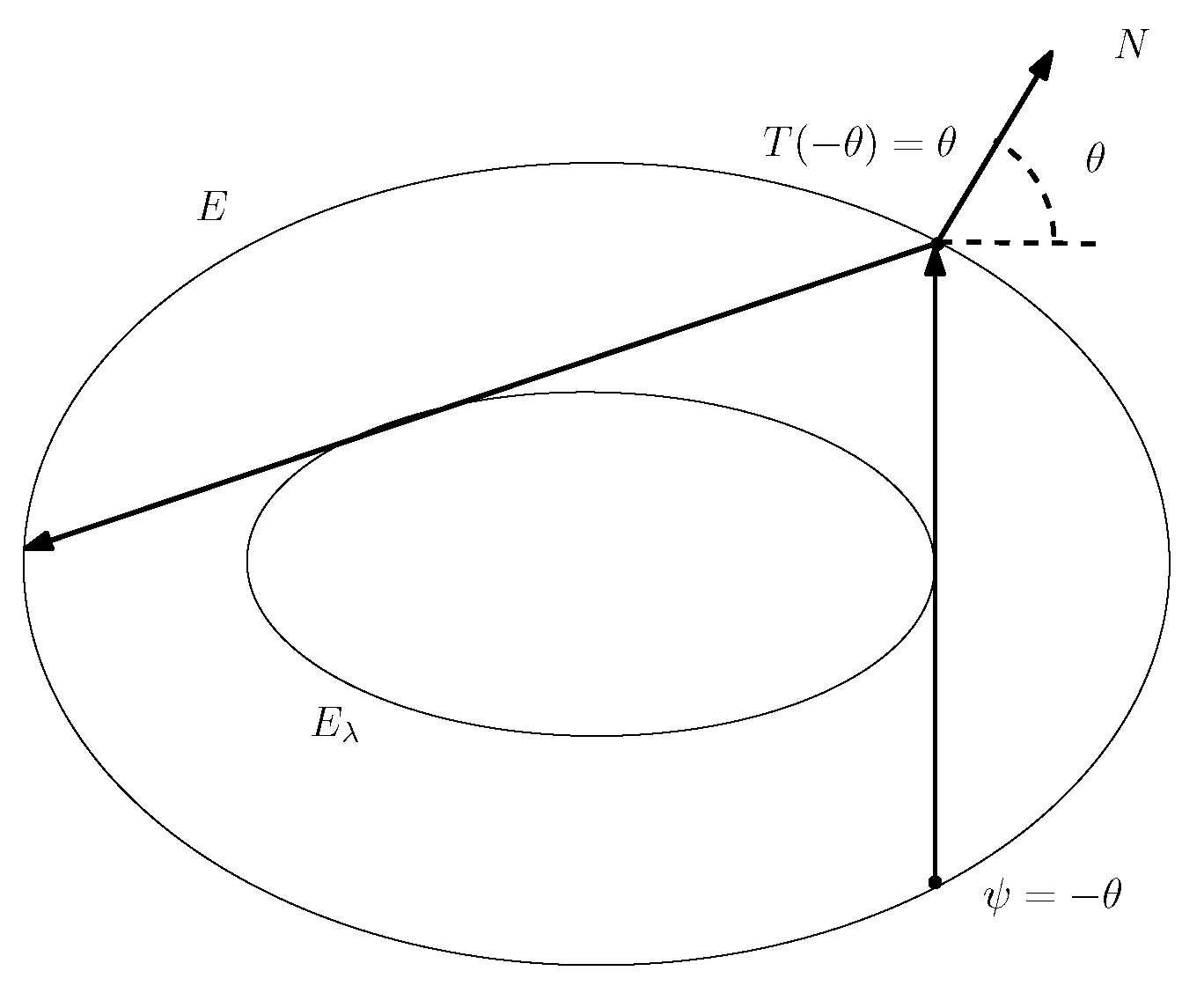
6. Mather β-Function and the Lazutkin Parameter
7. Rotation Number ρ
8. Mather β-Function and Rigidity
9. Discussion
- Is it possible to relax symmetry assumption in the main Theorem 1? Our method of proof of Theorem 1 relies on the approach related to the so-called E.Hopf type rigidity phenomenon from [18]. This method is very robust and it is not clear at the moment how it can be generalized.
- Another problem is to adopt our approach to a smaller neighborhood of the boundary of the phase cylinder.
- All known approaches to rigidity in billiards, are based on the properties of orbits near the boundary. We believe there are rigidity results based on the behavior far from the boundary.
- It would be interesting to prove that ellipse is determined by any two values of Mather function where are any two rotation numbers in .
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaloshin, V.; Sorrentino, A. On the local Birkhoff conjecture for convex billiards. Ann. Math. 2018, 188, 315–380. [Google Scholar] [CrossRef]
- Garcia, R.; Koiller, J.; Reznik, D. Estimating Elliptic Billiard Invariants with Spatial Integrals. J. Dyn. Control Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Suris, Y.B. Billiards in confocal quadrics as a pluri-Lagrangian system. Theor. Appl. Mech. 2016, 43, 221–228. [Google Scholar] [CrossRef]
- Bialy, M.; Mironov, A.E. Angular billiard and algebraic Birkhoff conjecture. Adv. Math. 2017, 313, 102–126. [Google Scholar] [CrossRef]
- Bialy, M. Gutkin billiard tables in higher dimensions and rigidity. Nonlinearity 2018, 31, 2281–2293. [Google Scholar] [CrossRef]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; Die Grundlehren der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1971; pp. xvi+358. [Google Scholar]
- Zelditch, S. (Northwestern University, Evanston, IL 60208, USA). Personal communication, August 2022.
- Zelditch, S. Survey on the inverse spectral problem. Not. Int. Congr. Chin. Math. 2014, 2, 1–20. [Google Scholar] [CrossRef]
- Chang, S.-J.; Friedberg, R. Elliptical billiards and Poncelet us theorem. J. Math. Phys. 1988, 29, 1537. [Google Scholar] [CrossRef]
- Dragović, V.; Radnović, M. Poncelet Porisms and Beyond. Integrable Billiards, Hyperelliptic Jacobians and Pencils of Quadrics; Frontiers in Mathematics; Birkhäuser/Springer Basel AG: Basel, Switzerland, 2011; pp. viii+293. [Google Scholar]
- Stachel, H. On the motion of billiards in ellipses. Eur. J. Math. 2022, 1–21. [Google Scholar] [CrossRef]
- Stachel, H. The geometry of billiards in ellipses and their Poncelet grids. J. Geom. 2021, 112, 1–29. [Google Scholar] [CrossRef]
- Tabanov, M.B. New ellipsoidal confocal coordinates and geodesics on an ellipsoid. Math. Sci. 1996, 82, 3851–3858. [Google Scholar] [CrossRef]
- Bialy, M.; Tabachnikov, S. Dan Reznik’s identities and more. Eur. J. Math. 2020, 1–14. [Google Scholar] [CrossRef]
- Reznik, D.; Garcia, R.; Koiller, J. Can the elliptic billiard still surprise us? Math. Intell. 2020, 42, 6–17. [Google Scholar] [CrossRef]
- Reznik, D.; Garcia, R.; Koiller, J. Fifty new invariants of N-periodics in the elliptic billiard. Arnold Math. J. 2021, 7, 341–355. [Google Scholar] [CrossRef]
- Akopyan, A.; Schwartz, R.; Tabachnikov, S. Billiards in ellipses revisited. Eur. J. Math. 2020, 1–15. [Google Scholar] [CrossRef]
- Bialy, M.; Mironov, A.E. The Birkhoff-Poritsky conjecture for centrally-symmetric billiard tables. Ann. Math. 2022, 196, 389–413. [Google Scholar] [CrossRef]
- Siburg, K.F. The Principle of Least Action in Geometry and Dynamics; Lecture Notes in Mathematics, 1844; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Hezari, H.; Zelditch, S. One can hear the shape of ellipses of small eccentricity. arXiv 2019, arXiv:1907.03882. [Google Scholar] [CrossRef]
- Huang, G.; Kaloshin, V.; Sorrentino, A. On the marked length spectrum of generic strictly convex billiard tables. Duke Math. J. 2018, 167, 175–209. [Google Scholar] [CrossRef]
- Sorrentino, A. Computing Mather’s β-function for Birkhoff billiards. Discrete Contin. Dyn. Syst. 2015, 35, 5055–5082. [Google Scholar] [CrossRef]
- Tabachnikov, S. Geometry and Billiards; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Kołodziej, R. The rotation number of some transformation related to billiards in an ellipse. Studia Math. 1985, 81, 293–302. [Google Scholar] [CrossRef]
- Mather, J.N. Differentiability of the minimal average action as a function of the rotation number. Bol. Soc. Brasil. Mat. 1990, 21, 59–70. [Google Scholar] [CrossRef]
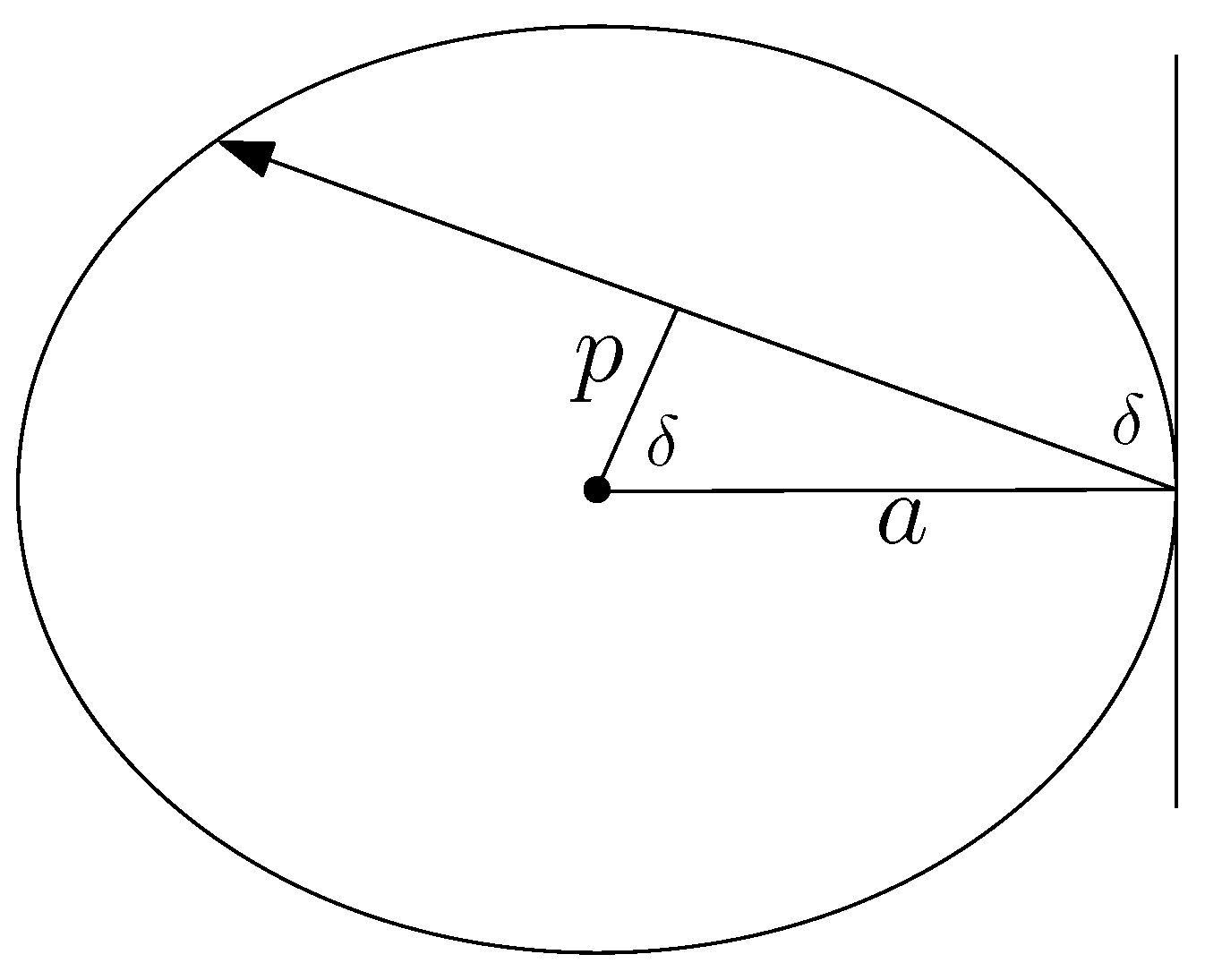
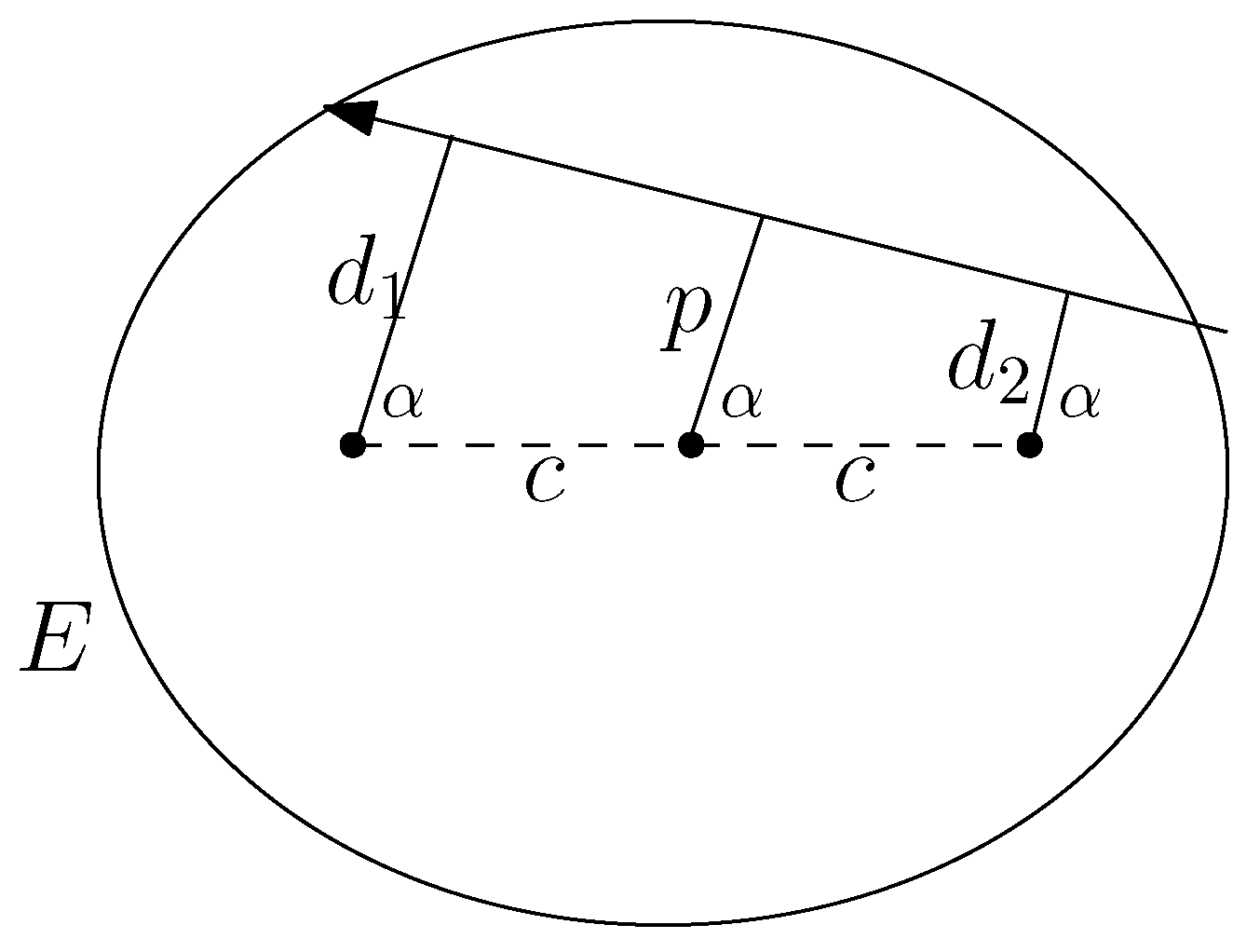

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bialy, M. Mather β-Function for Ellipses and Rigidity. Entropy 2022, 24, 1600. https://doi.org/10.3390/e24111600
Bialy M. Mather β-Function for Ellipses and Rigidity. Entropy. 2022; 24(11):1600. https://doi.org/10.3390/e24111600
Chicago/Turabian StyleBialy, Michael. 2022. "Mather β-Function for Ellipses and Rigidity" Entropy 24, no. 11: 1600. https://doi.org/10.3390/e24111600
APA StyleBialy, M. (2022). Mather β-Function for Ellipses and Rigidity. Entropy, 24(11), 1600. https://doi.org/10.3390/e24111600





