Abstract
This contribution considers proto-cell structures associated with asymmetries, mainly gravity, in the framework of reaction–diffusion. There are equivalent solutions for defined morphogen parameters in the equations that allow for defining proto-tissue complexity and configurational entropy. Using RNA data, improvements to the complexity and entropy due to the Earth’s gravity are presented. The theoretical proto-tissues complexity estimation, as a function of arbitrary surface gravity, is likewise proposed. In this sense, hypothetical aggregates of proto-cells on Mars would have a lower complexity than on Earth, which is equally valid for the Moon. Massive planets, or exoplanets like BD+20594b, could have major proto-tissue complexity and, eventually, rich biodiversity.
1. Introduction
Life on Earth began about one billion years ago [1,2], but what life is seems still to be an intricate question [3,4]. However, the understanding of the concept of life [4] as a self-sufficient physicochemical system, developed under Darwinian evolution theory, remains an adequate framework. This paper considers a way to achieve elementary prebiotic structures from an out-of-equilibrium point of view [5,6] when asymmetries, such as gravity, are present. In addition, amino acids exist in meteorites [7,8]; consequently, this work ignores a particular type of reactive element at this stage. I emphasize the generation, not of an isolated cell, but of a structure comprising elementary proto-cells. This is the framework of so-called complex systems, and the concept of morphogenesis [9,10,11,12]. Meanwhile, the relevant conception of inheritance will be explicitly considered in the sense of viability through adaptation in open systems.
Morphogenesis is related to the processes that turn undifferentiated cells into differentiated ones. Remarkably, cells do not contain the differentiation information which is stored in their relative and surrounding position [9,10,11]. That is, cell differentiation is a response to spatial location. Hence, privileging one direction, gravity must play a role in morphogenesis.
The information received by cells in the morphogenesis process is provided by basic physicochemical configurations. These spatial and temporal configurations are based on reagents called morphogens [9,10,11]. In practical terms, morphogen configurations are the previous scheme where the differentiation of cells is accommodated.
The following concepts [11] are adopted as a framework and used in the construction of a proto-tissue model in a finite spatial region [12]:
- Replication. Reactants interact to produce compound mainly from another chemical compound, substrate . Metabolism is assumed implicitly in the replication process. This process retains a sense of order which will be measured in terms of configuration entropy.
- Variation. Spatial patterns (containing “bricks” of ) have multiple and equivalent forms for fixed values of physical and chemical parameters. This is the analog to the concept of degeneration of states in physics.
- Heredity. On a large scale of perturbations, there is a viable continuity of equivalent traits (patterns) promoting adaptation.
Points (a) and (b) are linked to physicochemical procedures when compound corresponds to the morphogen. Statement (c) is a necessary condition of living systems [11]. In this sense, inheritance is related to the formation of equivalent structures and viability. Here, an observation is necessary. Living systems, not their origins, can be characterized by the operative concept called autopoiesis [13,14,15,16,17,18], i.e., the robustness of internal cycles faces external disturbances, among other fundamental properties. From this point on, nonlinear reaction equations can provide limit cycles that satisfy this requirement.
In this paper, reaction–diffusion equations for chemical reagents are proposed. Consider two chemical compounds, (the morphogen) and (the substrate), in a given spatial region and the reaction process:
These reactions are somewhat different from Schnackenberg’s usual model [19,20,21,22,23], where the latter term operates as . In the above process, the final configuration for “bricks” , the morphogen, is built more quickly as it requires only one element to generate the reaction.
In order to facilitate the understanding of this work, a brief description of the sections and their articulations will be given here. In Section 2, based on the reaction process between the chemical reagents, the evolution equations for the concentrations of morphogens and substrates are proposed. These equations incorporate spatial (diffusion) and nonlinear elements. Emphasis is placed on directional asymmetries and spatial growth conditions for the morphogen. Section 3 considers stationary solutions related to the degeneration ellipsoid that allows the researcher to define the number of equivalent states. Section 4 constructs an explicit example of proto-tissues based on the solutions in the previous section. Section 5 is the largest contribution in the field defined as “life”. The concept of complexity of a proto-tissue is defined simply, and intuitively, as that related to the number of accessible states of the system. In addition, the entropy is evaluated in direct terms of the parameters. In this section, estimates are made based on terrestrial parameters and RNA. In Section 6, the most hypothetical, the complexity of proto-tissues is evaluated based on the acceleration of gravity for different planets and exoplanets. Some conjectures are considered in relation to biodiversity and gravity. The last section is devoted to the relevant conclusions of this work.
2. Reaction–Diffusion for Proto-Tissues
The law of mass action, associated with the above-mentioned chemical processes, suggests the evolution equations for concentration variations and :
Parameters , and are the usual chemical rates, and is the diffusion tensors that promote cross-diffusion and spatial asymmetries such as gravity. The above set supports uniform solutions, i.e., = constant and = constant. In addition, and by simplicity, the concentrations are assumed to be dimensionless, for example, the number of molecules per mole.
The interest is in asymmetric spatial configurations where gravity plays a role in cell differentiation. For example, consider tiny asymmetric diffusion coefficients like
A key point exploited in this work is that through fixed solution , Equation (1) is formally linear in A and supports superposition. That is, if there are multiple equivalent solutions for a given , these solutions can be added together due to the particular linearity of Equation (1). In addition, from the expected growth of species ; condition [12]
applies, which is required for new emerging structures due to the instability of old configurations. This means the growth rate for is greater than its destruction rate. Furthermore, from Equations (1) and (2) results the constraint
Finally, semi-analytical solutions of the Schnakenberg equation were considered in reference to Noufaey [23]. It contains limit cycles, an important notion for autopoiesis [13,14,15,16,17,18] as a framework to characterize life.
3. Stationary States: Equivalent Solutions and a Comprehensive Complexity Measure
General solutions of Equations (1) and (2) are difficult to achieve, so if the focus remains on stationary states with wave-vector , consider:
From Equations (1) and (2) emerge the algebraic equations for amplitudes and given by
The first equation, with assumed amplitude , defines an n-dimensional ellipsoid in -space (see Equation (4)):
where consequently, there are many equivalent wave-vectors for a given value of amplitude . As an example, solving for in Equation (10), Figure 1 shows the function in spatial dimension two for an isotropic system where the equivalent states (degeneration) are defined by a circle related to a cutting plane. Note the formal similarity of Equation (10) with the Dirac equation for massive fermions, with playing the role of mass.
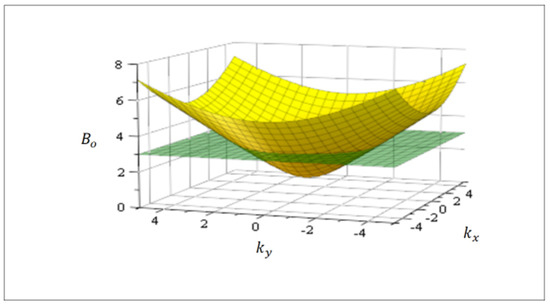
Figure 1.
Amplitude in Equation (10) for an isotropic diffusion tensor in dimension two. For a fixed value of , there is a sub-space (circle, green cutting plane) in the k-space displaying multiple equivalent solutions (complexity). These equivalent solutions can be superposed in Equation (1) which becomes lineal in this sub-space (Section 4).
On the other hand, for different values of , the morphogen amplitude formally follows from Equation (9) such as
marking the “uncertainty principle” which requires and, the equality becomes valid at low diffusion ().
4. Constructing Proto-Cell Aggregates (Tissues)
For a given amplitude in the space of wave-vectors of spatial dimension , there is a set of equivalent wave-vectors on the surface of the n-dimensional ellipsoid Equation (10). For instance, for a diagonal matrix like Equation (3), the following four fixed wave-vectors have equivalents in dimension two:
At this stage, for the same related to the above-defined four vectors, Equation (1) is lineal for concentration . The superposed solution exists and can be re-arranged as:
Figure 2 shows this kind of proto-tissue solution.
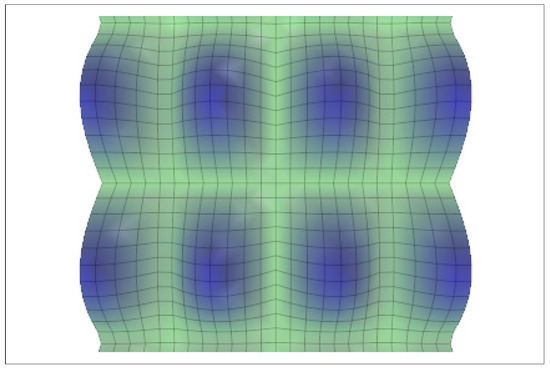
Figure 2.
Proto-cell aggregates. If there is a set of equivalent solutions defined by Equation (10), the superposition of two or more of them is possible (Equation (1) becomes linear). The figure exhibits the morphogen superposition for (with ). It describes a proto-tissue configuration or pattern. Other configurations related to hexagons, for example, are also possible.
Finally, general stationary solutions can be written as , with in the n-dimensional ellipsoid defined by Equation (10). Remarkably, these kind of solutions are not approximates.
5. Proto-Tissue Complexity and Entropy from RNA Estimation on Earth
The condition for the generation of new structures or tissues was considered in detail by Flores [12], but here it is assumed the condition established in Equation (4) suffices.
Equation (10) defines an n-dimensional ellipsoid for the wave vector in the space of dimension with volume: ( semi-axes). Assuming asymmetry in the z-direction (), the dimensionless volume in phase space corresponds to:
being, as usual in statistical mechanics [24,25,26,27], the number of equivalent configurations (complexity) for a given substrate . Additionally, it allows defining the configuration entropy associated with these proto-cell structures. Note that in Equation (14), the spatial dimension can also be assumed to be fractional [12].
At this point, a consideration must be made. -vectors run along the surface of the ellipsoid defined by Equation (10) and this surface is linked to entropy (Boltzmann’s entropy). However, in this paper we consider rather the volume of the ellipsoid (Gibbs’ entropy). In this sense, the measure related to Equation (14) corresponds to a finite range of values.
Without asymmetries (i.e., when ). The complexity parameter Equation (14) is reformulated as
Consequently, asymmetries change complexity or the number of equivalent configurations. Moreover, always from Equation (14), the configuration entropy becomes
with being the residual entropy (Figure 3).
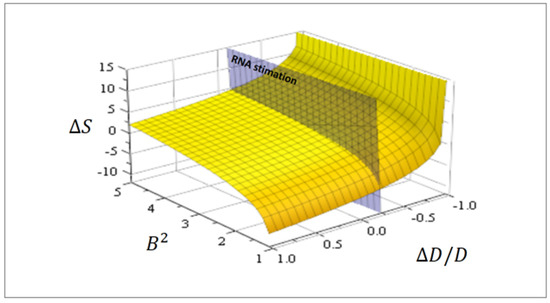
Figure 3.
The effective proto-tissue configuration entropy Equation (16) as a function of asymmetry of the diffusion coefficient and normalized substrate concentration . The plane cutting the surface corresponds to , an RNA estimation related to Earth gravity.
The Einstein relation between diffusion coefficient and collision time is given by (m mass). Accordingly, for enlarged collision time , the diffusion coefficient diminishes and the entropy grows (Figure 3). In other words, from Equation (15), asymmetries promote complexities.
Explicitly, due to gravity , assume
When a characteristic linear size and an estimation for RNA [m], then [m2/s]. A diffusion coefficient [m2/s] seems always appropriate [28] for RNA, and then due to gravity . The plane cutting the surface in Figure 3 corresponds to this value. In addition, using Equation (15), the relative number of configurations attributable to gravity can be estimated in this case as 1.15, hence gravity promoted complexity in proto-tissue constructions on Earth.
6. Proto-Tissue Complexity and Planetary Gravity: Comparison with Earth
Provided that Equations (15) and (17) hold, and expanding in the parameter , complexity variations for proto-tissues become related to gravity through . This way, there is a simple correlation for complexity for two different planets ( and ) where proto-tissues could eventually be generated:
Figure 4 shows this correlation as a function of arbitrary gravities and . As an eventual estimation, on Mars [m/s2] and on Earth [m/s2]. Consequently, the correlation between degrees of proto-tissue complexity on both planets is hypothetically like .
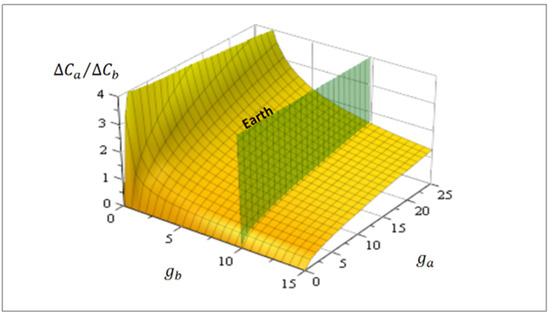
Figure 4.
Eventual proto-tissues correlation for complexity for two hypothetical planets (Equation (18)) as a function of their surface gravity and . The green cutting plane represents Earth [m/s2] and planets with relatively larger gravity have, in due course, proto-tissues with major structural complexity. In the Mars case, [m/s2], hypothetical proto-tissues have minor complexity compared to Earth because .
Always in Figure 4, the green plane cutting the surface corresponds to Earth’s gravity, so more massive planets or exoplanets [29,30] ( [m/s2]) possess hypothetically more complex proto-tissue structures and, it may be surmised, supposedly major biodiversity.
Using Earth as patron of proto-tissue complexity with value , Equation (18) can be reformulated for any body with surface gravity [m/s2] as
Largely hypothetical, Figure 5 shows the supposed proto-tissue complexity as a function of (approximate) surface gravity for different astronomical bodies in the solar system and some exoplanets. For instance, Pluto has relative complexity and Triton and, theoretically, proto-tissues could be less complex there than on Earth.
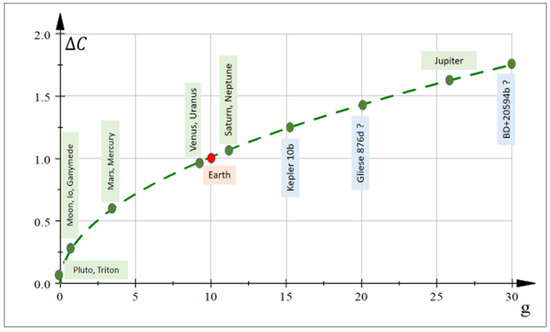
Figure 5.
Hypothetical proto-tissue complexity (Equation (19)) for different planets, moons and exoplanets as a function of their respective gravitational parameter [m/s2]. Earth is assumed to be a reference point, with proto-tissue complexity equal to 1 (red point). The Moon has relative complexity and Mars . In these two corps, hypothetical proto-tissue configurations could be less complex than on Earth. Jupiter with large gravitational constant [m/s2] could eventually possess a complexity of proto-cell aggregates larger than Earth.
7. Conclusions and Scopes
Generally, and keeping Earth as reference, there are optimal parameters for hypothetical life on planets or exoplanets [31,32,33,34,35,36,37]. In this way, this work contribution is connected to stationary proto-cellular structures with asymmetries (gravity [38]).
From the proposed reaction–diffusion equations, even featuring nonlinear equations, this model supports the superposition of solutions when the wave vector remains in a well-defined n-dimensional ellipsoidal sub-space (Section 3). In this sub-space exists equivalent solutions which allow for defining complexity and entropy (Section 5). This idea discussed in this paper has a degree of similarity to the notion of size-complexity discussed by Bonner [39]. Also, it is worth mentioning that there are other ways to quantitatively characterize the complexity in different systems [40]. Accordingly, using RNA-related data, corrections in the diffusion coefficient, complexity, and entropy due to Earth’s gravity were evaluated.
The results obtained in this work are valid for finite and relatively quiet environments where diffusion plays a fundamental role. On Earth, this may be important considering that conditions in the prebiotic era were probably extremely aggressive and variable. Phenomena such as turbulence can alter the nature of the solutions proposed here and eliminate the characteristic patterns obtained for proto-tissues.
Theoretic estimates of proto-tissue complexity Equation (19) was proposed as a function of surface gravity for arbitrary planets that allow comparisons with terrestrial proto-tissue (Section 6). In this sense, hypothetical proto-cell aggregates on Mars would have lower quantitative complexity than those on Earth, which would be equally valid for the Moon. On massive planets, or exoplanets such as BD+20594b, cellular proto-tissues would supposedly have greater complexity (Section 6, Figure 5).
Reaction–diffusion equations such as Equations (1) and (2) deserve an in-depth study from the dynamic point of view. That is, the formation of proto-tissue and its temporal evolution becomes the next step in this research. The notion of autopoiesis, particularly the idea of limit cycles acting in the context of life, should also be incorporated as a function of gravity.
Finally, and hypothetically, if great complexity of proto-tissues existed on (exo) planets with pronounced gravity, it is plausible to expect they also host large biodiversity when assuming the validity of Darwinian evolution theory in this context.
Funding
Funding received from Project UTA-Mayor 4739-20.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares to have no conflict of interest related to this research.
References
- Hazen, R.M. Life’s rocky start. Sci. Am. 2001, 284, 76–851. [Google Scholar] [CrossRef] [PubMed]
- Steel, M.; Penney, D. Common ancestry put to the test. Nature 2010, 465, 168–169. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Wath Is Life; Cambridge Universite Press: Cambridge, UK, 1944. [Google Scholar]
- Benner, S.A. Defining life. Astrobiology 2010, 10, 1021–1030. [Google Scholar] [CrossRef] [PubMed]
- Branscomb, E.; Russell, M.J. Turnstile and bifurcator: The disequilibrium converting engines that put metabolism on the road. Biochim. Biophys. Acta Bioenerg. 2013, 1827, 62–78. [Google Scholar] [CrossRef] [PubMed]
- Leyva, Y.; Martín, O.; García-Jacas, C.R. Constraining the prebiotic cell size limits in extremely hostile environments: A dynamics perspective. Astrobiology 2018, 18, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Dom, E.D.; Nealson, K.H.; Adami, C. Monomer abundance distribution patterns as a universal biosignature: Examples from terrestrial and digital life. J. Mol. Evol. 2011, 72, 283–295. [Google Scholar]
- Barge, L.M.; Branscomb, E.; Brucato, J.R.; Cardoso, S.S.S.; Cartwright, J.H.E.; Danielache, S.O.; Galante, D.; Kee, T.P.; Miguel, Y.; Mojzsis, S.; et al. Thermodynamics, Disequilibrium, Evolution: Far-from-equilibrium geological and chemical considerations for origin-of-life research. Orig. Life Evol. Biosph. 2017, 47, 39–56. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Maynard-Smith, J. Shaping Life: Gene, Embryo and Evolution; Weidenfield and Nicolson: London, UK, 1998. [Google Scholar]
- Maynard-Smith, J.; Szathmáry, E. The Origins of Life: From the Birth of Life to the Origin of Language; Oxford Press: Oxford, UK, 1999. [Google Scholar]
- Flores, J.C. Prebiotic Aggregates (Tissues) Emerging from Reaction–Diffusion: Formation Time, Configuration Entropy and Optimal Spatial Dimension. Entropy 2022, 24, 124. [Google Scholar] [CrossRef]
- Varela, F.J.; Maturana, H.R.; Uribe, R. Autopoiesis: The organization of living systems, its characterization and a model. Biosystems 1974, 5, 187–196. [Google Scholar] [CrossRef]
- Maturana, H.R.; Varela, F.J. Autopoiesis and Cognition: The Realization of the Living; Reidel Publishing Company: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Veloz, T. Goals as Emergent Autopoietic Processes. Front. Bioeng. Biotechnol. 2021, 9, 720652. [Google Scholar] [CrossRef] [PubMed]
- Busseniers, E.; Veloz, T.; Heylighen, F. Goal Directedness, Chemical Organizations, and Cybernetic Mechanisms. Entropy 2021, 23, 1039. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D. An Investigation into the Origin of Autopoiesis. Artif. Life 2020, 26, 5–22. [Google Scholar] [CrossRef] [PubMed]
- Nousala, S.; Hall, W.P. Emerging Autopoietic Communities—Scalability of Knowledge Transfer in Complex Systems. In Proceedings of the 2008 IFIP International Conference on Network and Parallel Computing, Washington, DC, USA, 18–21 October 2008; pp. 418–425. [Google Scholar] [CrossRef][Green Version]
- Schnakenberg, J. Simple chemical reaction systems with limit cycle behavior. J. Theoret. Biol. 1979, 81, 389–400. [Google Scholar] [CrossRef]
- Haken, F. Synergetics, Introduction and Advanced Topics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Murray, J.D. Mathematical Biology I: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Murray, J.D. Mathematical Biology II: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Al Noufaey, K.S. Semi-analytical solutions of the Schnakenberg model of a reaction-diffusion cell with feedback. Results Phys. 2018, 9, 609–614. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics; Wiley and Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Landau, L.D.; Lifschitz, E.M. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Toda, M.; Kubo, R.; Saito, N. Statistical Physics I; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Pathria, R.K. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Lopez, A.; Fiore, M. Investigating Prebiotic Protocells for a Comprehensive Understanding of the Origins of Life: A Prebiotic Systems Chemistry Perspective. Life 2019, 9, 49. [Google Scholar] [CrossRef] [PubMed]
- Southworth, J.; Wheatley, P.J.; Sams, G. A method for the direct determination of surface gravities of transiting extrasolar planets. MNRAS Lett. 2007, 379, L11–L15. [Google Scholar] [CrossRef]
- Ballesteros, F.J.; Luque, B. Walking on Exoplanet. Astrobiology 2016, 16, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Makuch, D.; Heller, R.; Guinan, E. In Search for a Planet Better than Earth: Top Contenders for a Superhabitable World. Astrobiology 2020, 20, 1394–1404. [Google Scholar] [CrossRef]
- Mendez, A.; Rivera-Valentín, E.G.; Schulze-Makuch, D.; Filiberto, J.; Ramírez, R.M.; Wood, T.E.; Dávila, A.; McKay, C.; Ceballos, K.N.O.; Jusino-Maldonado, M.; et al. Habitability models for astrobiology. Astrobiology 2021, 21, 1017–1027. [Google Scholar] [CrossRef]
- Clark, B.C.; Kolb, V.; Steele, A.; House, C.; Lanza, N.; Gasda, P.; VanBommel, S.; Newsom, H.; Martínez-Frías, J. Origin of life on Mars: Suitability and opportunities. Life 2021, 11, 539. [Google Scholar] [CrossRef] [PubMed]
- Longo, A.; Damer, B. Factoring origin of life hypothesis into the search for life in the solar system and beyond. Life 2020, 10, 52. [Google Scholar] [CrossRef] [PubMed]
- Guttenberg, N.; Laneuville, M.; Ilardo, M.; Aubert-Kato, N. Transferable measurements of heredity in models of the origin of life. PLoS ONE 2015, 10, e0140663. [Google Scholar] [CrossRef] [PubMed]
- Arbesman, S.; Laughlim, G. A scientometric prediction of the discovery of the first potentially habitable planet with a mass similar to hearth. PLoS ONE 2010, 5, e13061. [Google Scholar] [CrossRef] [PubMed]
- Schleicher, D.R.G.; Bovino, S. The Fermi paradox: Impact of astrophysical processes and dynamical evolution. Int. J. Astrobiol. 2022, 1–14. [Google Scholar] [CrossRef]
- Kamal, K.Y.; Herranz, R.; Van Loon, J.J.W.A.; Medina, F.J. Simulated microgravity, mars gravity, and 2g hypergravity affect cell cycle regulation, ribosome biogenesis, and epigenetics in Arabidopsis cell cultures. Sci. Rep. 2018, 8, 6424. [Google Scholar] [CrossRef]
- Bonner, J.T. Perspective: The size-complexity rule. Evolution 2004, 58, 1883–1890. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).