An Information Theoretic Interpretation to Deep Neural Networks †
Abstract
:1. Introduction
2. Preliminaries and Methods
2.1. Methodological Background
2.2. Notations
2.3. Local Information Geometry
2.4. Modal Decomposition
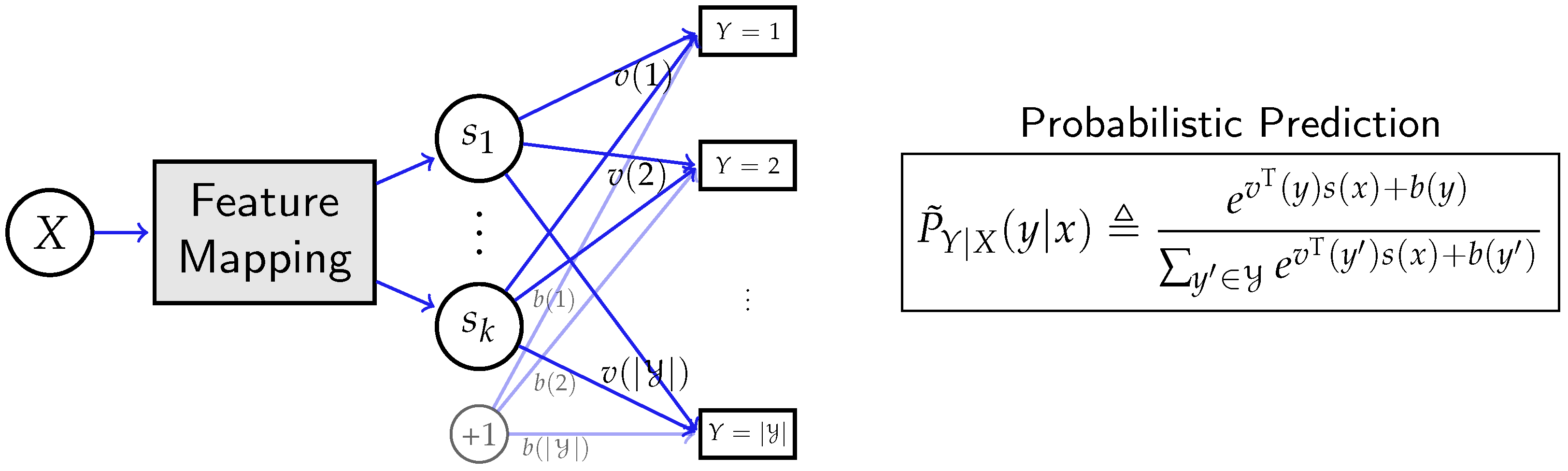
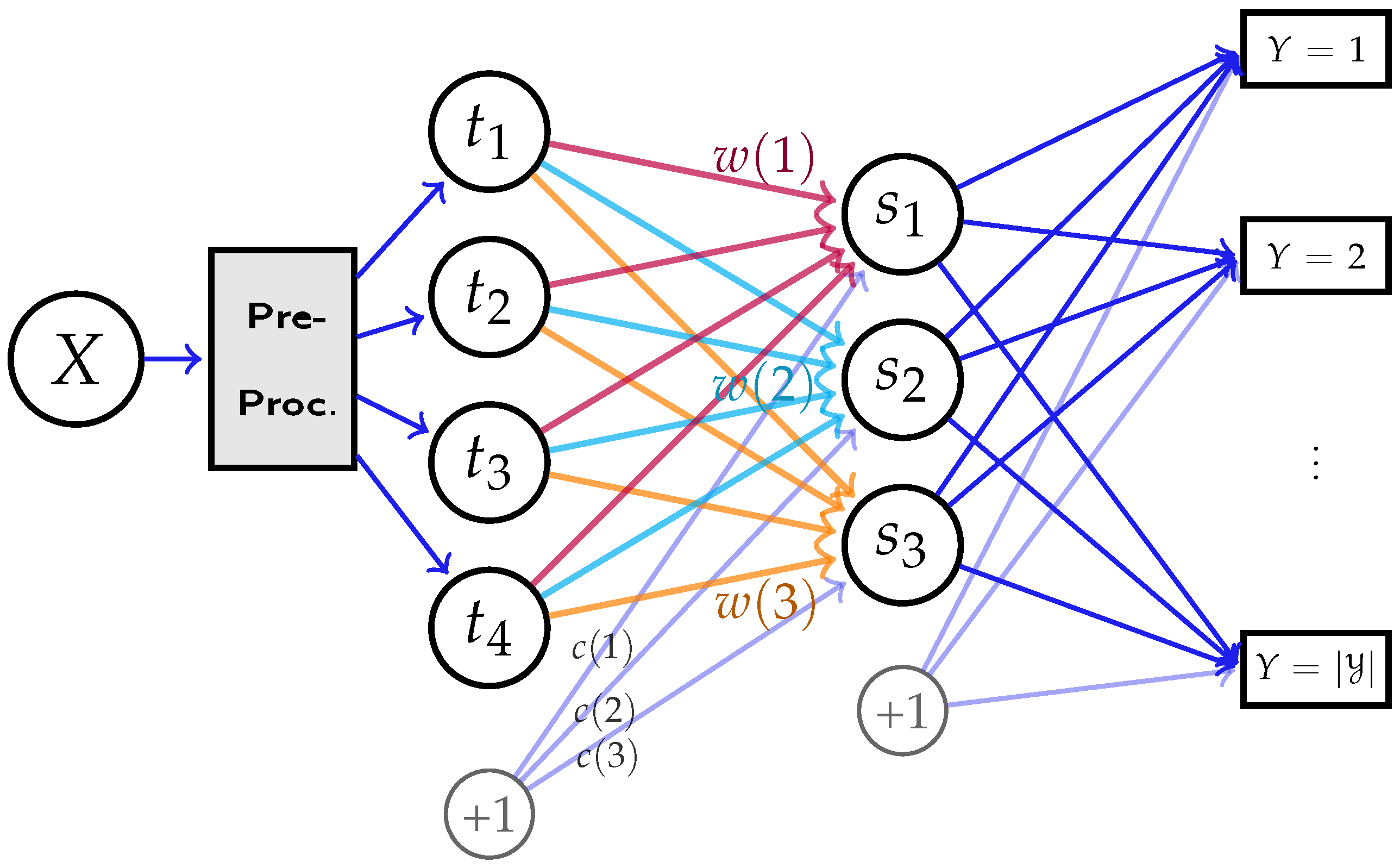
2.5. Deep Neural Networks
3. Results
3.1. Information-Theoretic Feature Selection
3.2. Feature Extraction in Deep Neural Networks
3.2.1. Network with Ideal Expressive Power
3.2.2. Network with Restricted Expressive Power
3.3. Scoring Neural Networks
3.4. Experiments
3.4.1. Experimental Validation of Theorem 4
3.4.2. Experimental Validation of Theorem 5
3.4.3. Experimental Validation of H-Score
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Lemma 2
Appendix C. Proof of Lemma 3
Appendix D. Proofs of Theorems 2 and 3
Appendix E. Proof of Theorem 4
Appendix F. Proof of Theorem 5
Appendix G. Analyses of Hidden Layer Parameters
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 3–5 June 2019; Volume 1 (Long and Short Papers). Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4171–4186. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 1877–1901. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Cully, A.; Togelius, J. Alphastar: An evolutionary computation perspective. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 314–315. [Google Scholar]
- MacKay, D.J.C. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521642989. [Google Scholar]
- Zintgraf, L.M.; Cohen, T.S.; Adel, T.; Welling, M. Visualizing Deep Neural Network Decisions: Prediction Difference Analysis. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Papyan, V.; Han, X.; Donoho, D.L. Prevalence of neural collapse during the terminal phase of deep learning training. Proc. Natl. Acad. Sci. USA 2020, 117, 24652–24663. [Google Scholar] [CrossRef]
- Adebayo, J.; Gilmer, J.; Muelly, M.; Goodfellow, I.; Hardt, M.; Kim, B. Sanity Checks for Saliency Maps. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. (CSUR) 2018, 51, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Jacot, A.; Gabriel, F.; Hongler, C. Neural Tangent Kernel: Convergence and Generalization in Neural Networks. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Mei, S.; Montanari, A.; Nguyen, P.M. A mean field view of the landscape of two-layer neural networks. Proc. Natl. Acad. Sci. USA 2018, 115, E7665–E7671. [Google Scholar] [CrossRef] [Green Version]
- Arora, S.; Du, S.; Hu, W.; Li, Z.; Wang, R. Fine-grained analysis of optimization and generalization for overparameterized two-layer neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 322–332. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Huang, S.L.; Xu, X.; Zheng, L.; Wornell, G.W. An information theoretic interpretation to deep neural networks. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1984–1988. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Goldfeld, Z.; Polyanskiy, Y. The information bottleneck problem and its applications in machine learning. IEEE J. Sel. Areas Inf. Theory 2020, 1, 19–38. [Google Scholar] [CrossRef]
- Huang, S.L.; Makur, A.; Zheng, L.; Wornell, G.W. An information-theoretic approach to universal feature selection in high-dimensional inference. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1336–1340. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, J.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Olga, R.; Jia, D.; Hao, S.; Jonathan, K.; Sanjeev, S.; Sean, M.; Zhiheng, H.; Andrej, K.; Aditya, K.; Michael, B.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.L.; Zheng, L. Linear information coupling problems. In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012; pp. 1029–1033. [Google Scholar]
- Huang, S.L.; Makur, A.; Wornell, G.W.; Zheng, L. On universal features for high-dimensional learning and inference. arXiv 2019, arXiv:1911.09105. [Google Scholar]
- Hirschfeld, H.O. A connection between correlation and contingency. Proc. Camb. Phil. Soc. 1935, 31, 520–524. [Google Scholar] [CrossRef]
- Gebelein, H. Das statistische problem der Korrelation als variations-und Eigenwertproblem und sein Zusammenhang mit der Ausgleichungsrechnung. Z. Angew. Math. Mech. 1941, 21, 364–379. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Dependence. Acta Math. Acad. Sci. Hung. 1959, 10, 441–451. [Google Scholar] [CrossRef]
- du Pin Calmon, F.; Makhdoumi, A.; Médard, M.; Varia, M.; Christiansen, M.; Duffy, K.R. Principal inertia components and applications. IEEE Trans. Inf. Theory 2017, 63, 5011–5038. [Google Scholar] [CrossRef] [Green Version]
- Hsu, H.; Asoodeh, S.; Salamatian, S.; Calmon, F.P. Generalizing bottleneck problems. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 531–535. [Google Scholar]
- Hsu, H.; Salamatian, S.; Calmon, F.P. Correspondence analysis using neural networks. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, PMLR, Okinawa, Japan,, 16–18 April 2019; pp. 2671–2680. [Google Scholar]
- Anantharam, V.; Gohari, A.; Kamath, S.; Nair, C. On hypercontractivity and a data processing inequality. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA,, 29 June–4 July 2014; pp. 3022–3026. [Google Scholar]
- Raginsky, M. Strong data processing inequalities and Φ-Sobolev inequalities for discrete channels. IEEE Trans. Inf. Theory 2016, 62, 3355–3389. [Google Scholar] [CrossRef] [Green Version]
- Polyanskiy, Y.; Wu, Y. Strong data-processing inequalities for channels and Bayesian networks. In Convexity and Concentration; Springer: Berlin/Heidelberg, Germany, 2017; pp. 211–249. [Google Scholar]
- Greenacre, M.J. Theory and Applications Of Correspondence Analysis; Academic Press: London, UK, 1984. [Google Scholar]
- Wang, H.; Vo, L.; Calmon, F.P.; Médard, M.; Duffy, K.R.; Varia, M. Privacy with estimation guarantees. IEEE Trans. Inf. Theory 2019, 65, 8025–8042. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H. Estimating Optimal Transformations for Multiple Regression and Correlation. J. Am. Stat. Assoc. 1985, 80, 614–619. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Neural Networks. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 389–416. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 12. [Google Scholar]
- Alain, G.; Bengio, Y. Understanding intermediate layers using linear classifier probes. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 1139–1147. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Bengio, Y., LeCun, Y., Eds.; Conference Track Proceedings. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–29 July 2017; Volume 1, p. 3. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–29 July 2017; pp. 1251–1258. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA,, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- Xu, X.; Huang, S.L.; Zheng, L.; Zhang, L. The geometric structure of generalized softmax learning. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018; pp. 1–5. [Google Scholar]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning structured sparsity in deep neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 2074–2082. [Google Scholar]
- Wang, L.; Wu, J.; Huang, S.L.; Zheng, L.; Xu, X.; Zhang, L.; Huang, J. An efficient approach to informative feature extraction from multimodal data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 5281–5288. [Google Scholar]
- Lee, J.; Sattigeri, P.; Wornell, G. Learning new tricks from old dogs: Multi-source transfer learning from pre-trained networks. Adv. Neural Inf. Process. Syst. 2019, 32, 4370–4380. [Google Scholar]
- Dembo, A.; Zeitouni, O. Large Deviations Techniques and Applications; Corrected Reprint of the Second (1998) Edition; Stochastic Modelling and Applied Probability; Springer: Berlin/Heidelberg, Germany, 2010; p. 38. [Google Scholar]
- Sason, I.; Verdú, S. f-divergence Inequalities. IEEE Trans. Inf. Theory 2016, 62, 5973–6006. [Google Scholar] [CrossRef]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]




| DNN Model | Paras [] | Accuracy [%] | ||
|---|---|---|---|---|
| VGG16 [44] | 138.4 | 148.3 | 41.9 | 64.2 |
| VGG19 [44] | 143.7 | 152.7 | 42.2 | 64.7 |
| MobileNet [45] | 4.3 | 45.9 | 42.6 | 68.4 |
| DenseNet121 [46] | 8.1 | 59.5 | 53.3 | 71.4 |
| DenseNet169 [46] | 14.3 | 81.2 | 70.2 | 73.6 |
| DenseNet201 [46] | 20.2 | 89.1 | 73.5 | 74.4 |
| Xception [47] | 22.9 | 179.8 | 162.2 | 77.5 |
| InceptionV3 [48] | 23.9 | 181.2 | 162.9 | 76.3 |
| InceptionResNetV2 [49] | 55.9 | 241.1 | 198.1 | 79.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Huang, S.-L.; Zheng, L.; Wornell, G.W. An Information Theoretic Interpretation to Deep Neural Networks. Entropy 2022, 24, 135. https://doi.org/10.3390/e24010135
Xu X, Huang S-L, Zheng L, Wornell GW. An Information Theoretic Interpretation to Deep Neural Networks. Entropy. 2022; 24(1):135. https://doi.org/10.3390/e24010135
Chicago/Turabian StyleXu, Xiangxiang, Shao-Lun Huang, Lizhong Zheng, and Gregory W. Wornell. 2022. "An Information Theoretic Interpretation to Deep Neural Networks" Entropy 24, no. 1: 135. https://doi.org/10.3390/e24010135
APA StyleXu, X., Huang, S.-L., Zheng, L., & Wornell, G. W. (2022). An Information Theoretic Interpretation to Deep Neural Networks. Entropy, 24(1), 135. https://doi.org/10.3390/e24010135







