Probabilistic Deterministic Finite Automata and Recurrent Networks, Revisited
Abstract
:1. Introduction
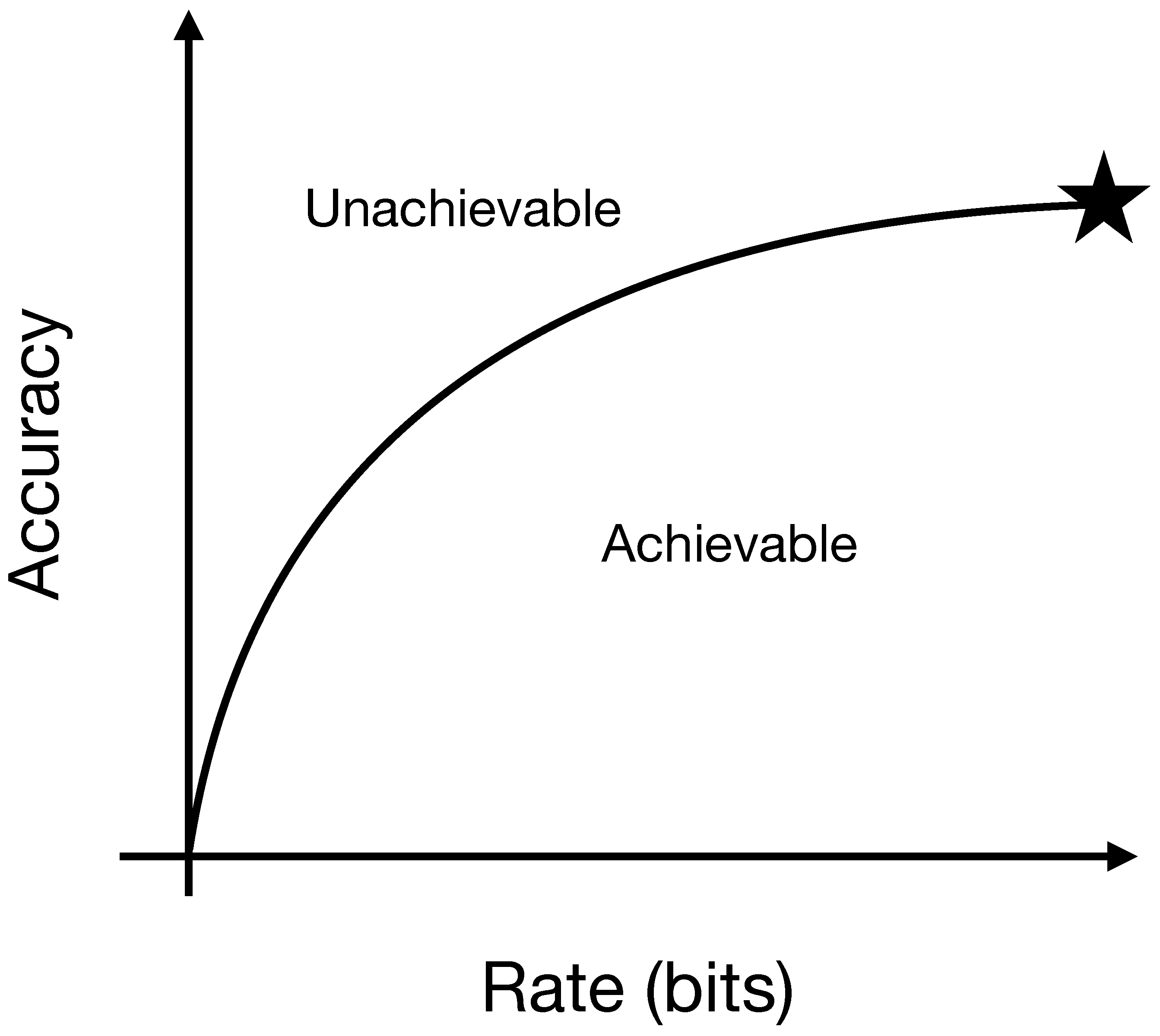
2. Rate-Distortion Benchmarks for Prediction Algorithms
3. Background
3.1. PDFAs and Predictive Rate-Distortion
3.2. Time Series Methods
4. Results
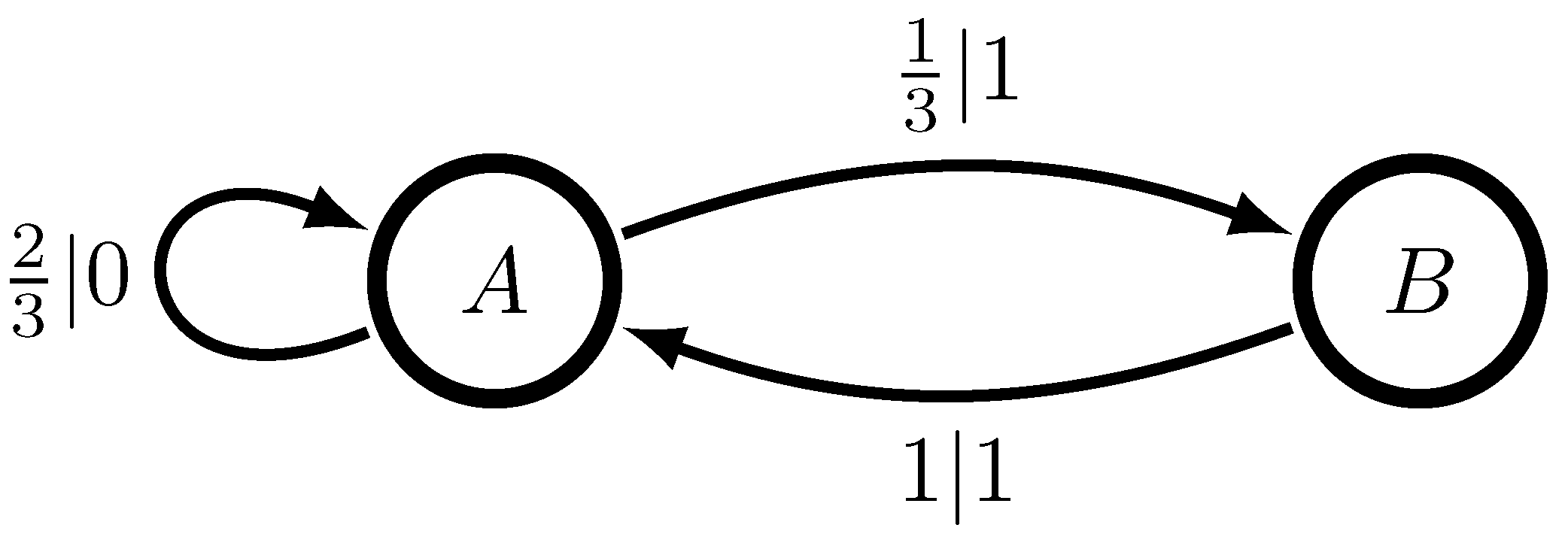
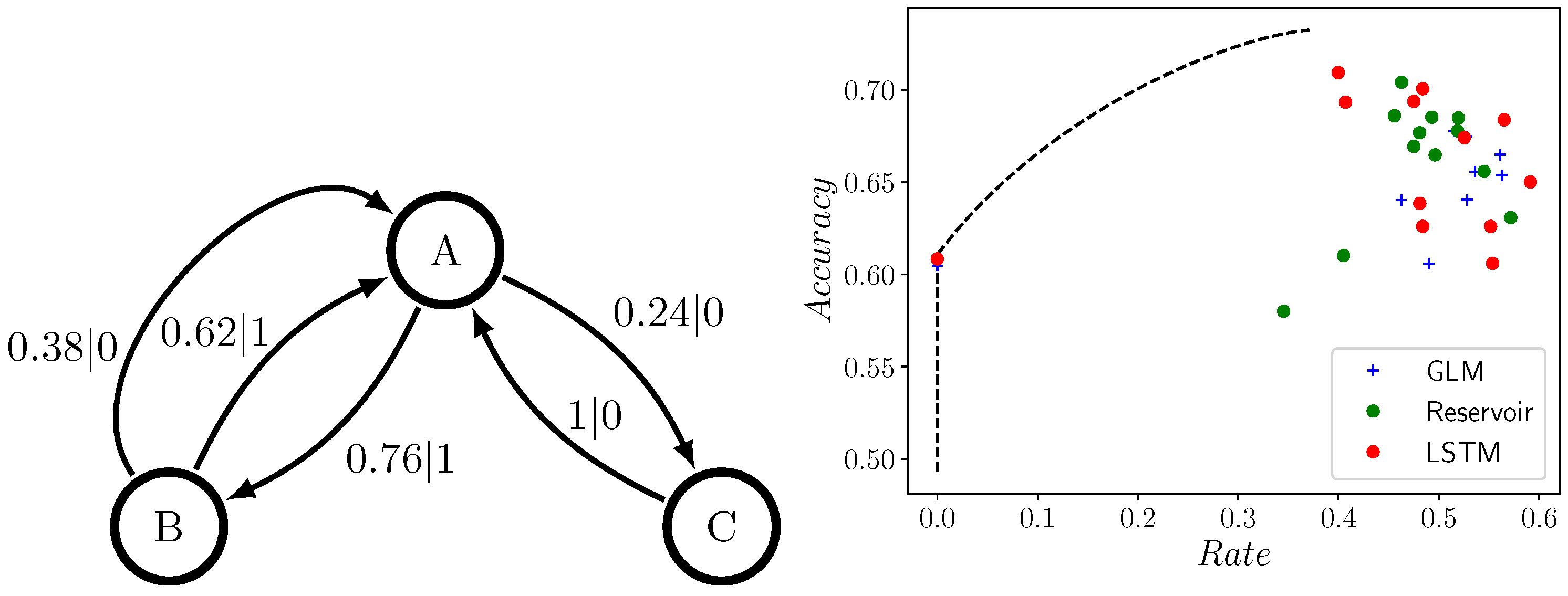
4.1. The Difference between Theory and Practice: The Even and Neven Process
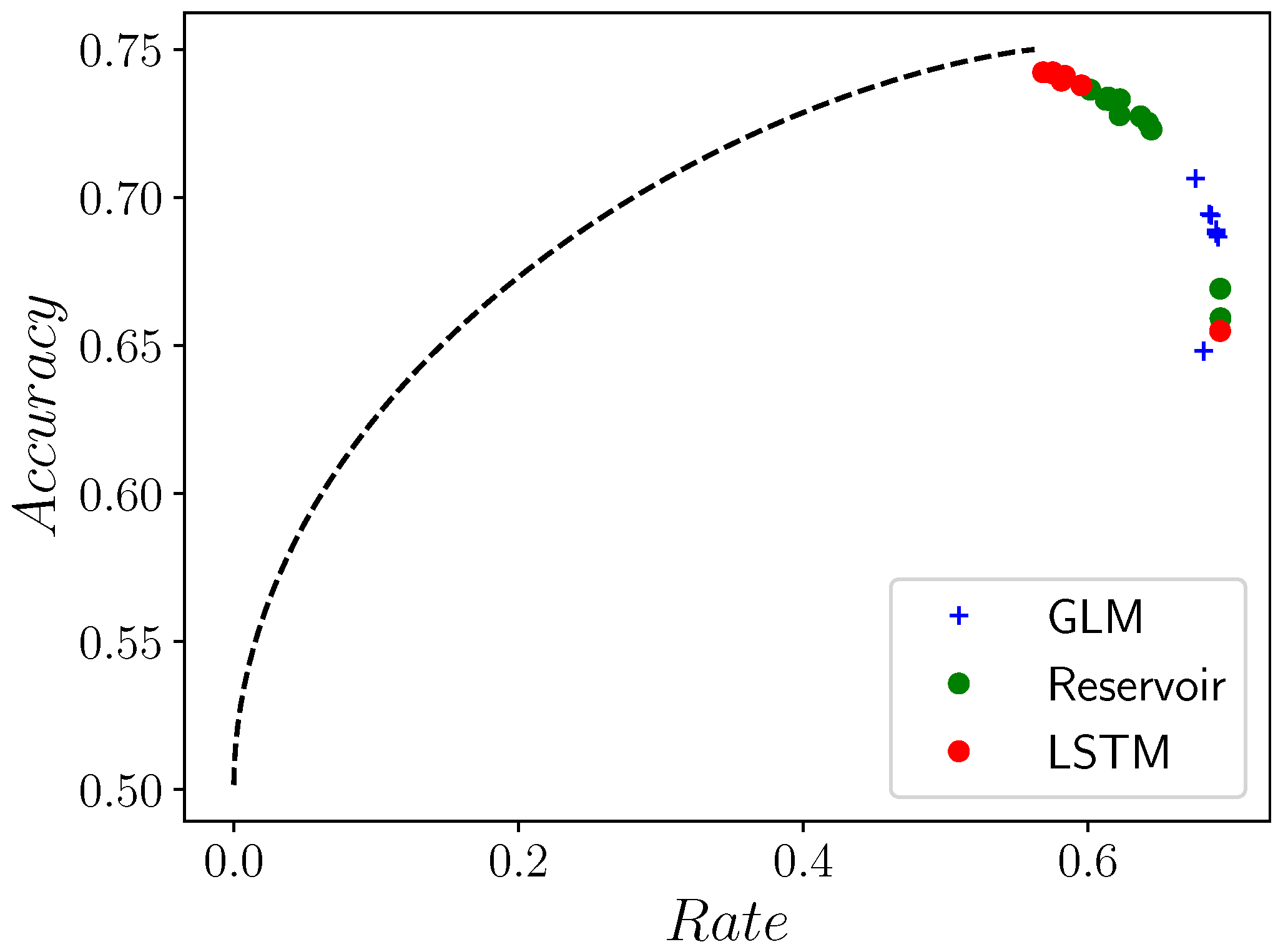
4.2. Comparing GLMs, RCs, and LSTMs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schultz, W.; Dayan, P.; Montague, P.R. A neural substrate of prediction and reward. Science 1997, 275, 1593–1599. [Google Scholar] [CrossRef] [Green Version]
- Montague, P.R.; Dayan, P.; Sejnowski, T.J. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 1996, 16, 1936–1947. [Google Scholar] [CrossRef] [Green Version]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79. [Google Scholar] [CrossRef]
- Berger, T. Rate Distortion Theory; Prentice-Hall: New York, NY, USA, 1971. [Google Scholar]
- Still, S.; Crutchfield, J.P.; Ellison, C.J. Optimal causal inference: Estimating stored information and approximating causal architecture. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 037111. [Google Scholar] [CrossRef] [Green Version]
- Still, S. Information bottleneck approach to predictive inference. Entropy 2014, 16, 968–989. [Google Scholar] [CrossRef] [Green Version]
- Marzen, S.; Crutchfield, J.P. Predictive Rate-Distortion for Infinite-Order Markov Processes. J. Stat. Phys. 2014, 163, 1312–1338. [Google Scholar] [CrossRef] [Green Version]
- Palmer, S.E.; Marre, O.; Berry, M.J.; Bialek, W. Predictive information in a sensory population. Proc. Natl. Acad. Sci. USA 2015, 112, 6908–6913. [Google Scholar] [CrossRef] [Green Version]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Ash, R.B. Information Theory; John Wiley and Sons: New York, NY, USA, 1965. [Google Scholar]
- Shalizi, C.R.; Crutchfield, J.P. Computational Mechanics: Pattern and Prediction, Structure and Simplicity. J. Stat. Phys. 2001, 104, 817–879. [Google Scholar] [CrossRef]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Comput. 2001, 13, 2409–2463. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities Unseen, Randomness Observed: Levels of Entropy Convergence. Chaos 2003, 13, 25–54. [Google Scholar] [CrossRef] [PubMed]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef]
- Grigoryeva, L.; Ortega, J.P. Echo state networks are universal. Neural Netw. 2018, 108, 495–508. [Google Scholar] [CrossRef] [Green Version]
- Doya, K. Universality of Fully Connected Recurrent Neural Networks; Technology Report; Deptartment of Biology, UCSD: La Jolla, CA, USA, 1993. [Google Scholar]
- Cleeremans, A.; Servan-Schreiber, D.; McClelland, J.L. Finite state automata and simple recurrent networks. Neural Comput. 1989, 1, 372–381. [Google Scholar] [CrossRef]
- Horne, B.G.; Hush, D.R. Bounds on the complexity of recurrent neural network implementations of finite state machines. In Proceedings of the 6th International Conference on Neural Information Processing Systems, Denver, CO, USA, 29 November–2 December 1993; pp. 359–366. [Google Scholar]
- Schmidhuber, J.; Hochreiter, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Collins, J.; Sohl-Dickstein, J.; Sussillo, D. Capacity and trainability in recurrent neural networks. arXiv 2016, arXiv:1611.09913. [Google Scholar]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Stoc. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Strelioff, C.C.; Crutchfield, J.P. Bayesian Structural Inference for Hidden Processes. Phys. Rev. E 2014, 89, 042119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crutchfield, J.P.; Young, K. Inferring Statistical Complexity. Phys. Rev. Let. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Pfau, D.; Bartlett, N.; Wood, F. Probabilistic deterministic infinite automata. Adv. Neural Inf. Process. Syst. 2010, 23, 1930–1938. [Google Scholar]
- Littman, M.L.; Sutton, R.S. Predictive representations of state. Adv. Neural Inf. Process. Syst. 2002, 14, 1555–1561. [Google Scholar]
- Creutzig, F.; Sprekeler, H. Predictive coding and the slowness principle: An information-theoretic approach. Neural Comput. 2008, 20, 1026–1041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Creutzig, F.; Globerson, A.; Tishby, N. Past-future information bottleneck in dynamical systems. Phys. Rev. E 2009, 79, 041925. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley: Reading, MA, USA, 1979. [Google Scholar]
- James, R.G.; Mahoney, J.R.; Ellison, C.J.; Crutchfield, J.P. Many Roads to Synchrony: Natural Time Scales and Their Algorithms. Phys. Rev. E 2014, 89, 042135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Löhr, W. Models of Discrete-Time Stochastic Processes and Associated Complexity Measures. Ph.D. Thesis, University of Leipzig, Leipzig, Germany, 2009. [Google Scholar]
- Shalizi, C.R.; Shalizi, K.L.; Crutchfield, J.P. Pattern discovery in time series, Part I: Theory, algorithm, analysis, and convergence. J. Mach. Learn. Res. 2002, 10, 60. [Google Scholar]
- Csiszár, I. On the computation of rate-distortion functions (corresp.). IEEE Trans. Inf. Theory 1974, 20, 122–124. [Google Scholar] [CrossRef]
- Johnson, B.D.; Crutchfield, J.P.; Ellison, C.J.; McTague, C.S. Enumerating Finitary Processes. arXiv 2010, arXiv:1011.0036. [Google Scholar]
- Crutchfield, J.P.; Young, K. Computation at the Onset of Chaos. In Entropy, Complexity, and the Physics of Information; Zurek, W., Ed.; SFI Studies in the Sciences of Complexity; Addison-Wesley: Reading, MA, USA, 1990; Volume VIII, pp. 223–269. [Google Scholar]
- Packard, N.H. Adaptation toward the Edge of Chaos. In Dynamic Patterns in Complex Systems; Kelso, J.S., Mandell, A.J., Shlesinger, M.F., Eds.; World Scientific: Singapore, 1988; pp. 293–301. [Google Scholar]
- Mitchell, M.; Crutchfield, J.P.; Hraber, P. Dynamics, Computation, and the “Edge of Chaos”: A Re-Examination. In Complexity: Metaphors, Models, and Reality; Cowan, G., Pines, D., Melzner, D., Eds.; Santa Fe Institute Studies in the Sciences of Complexity; Addison-Wesley: Reading, MA, USA, 1994; Volume XIX, pp. 497–513. [Google Scholar]
- Mitchell, M.; Hraber, P.; Crutchfield, J.P. Revisiting the Edge of Chaos: Evolving Cellular Automata to Perform Computations. Complex Syst. 1993, 7, 89–130. [Google Scholar]
- Bertschinger, N.; Natschläger, T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. 2004, 16, 1413–1436. [Google Scholar] [CrossRef]
- Boedecker, J.; Obst, O.; Lizier, J.T.; Mayer, N.M.; Asada, M. Information processing in echo state networks at the edge of chaos. Theory Biosci. 2012, 131, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness-Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zaslavsky, N.; Kemp, C.; Regier, T.; Tishby, N. Efficient compression in color naming and its evolution. Proc. Natl. Acad. Sci. USA 2018, 115, 7937–7942. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzen, S.E.; Crutchfield, J.P. Probabilistic Deterministic Finite Automata and Recurrent Networks, Revisited. Entropy 2022, 24, 90. https://doi.org/10.3390/e24010090
Marzen SE, Crutchfield JP. Probabilistic Deterministic Finite Automata and Recurrent Networks, Revisited. Entropy. 2022; 24(1):90. https://doi.org/10.3390/e24010090
Chicago/Turabian StyleMarzen, Sarah E., and James P. Crutchfield. 2022. "Probabilistic Deterministic Finite Automata and Recurrent Networks, Revisited" Entropy 24, no. 1: 90. https://doi.org/10.3390/e24010090
APA StyleMarzen, S. E., & Crutchfield, J. P. (2022). Probabilistic Deterministic Finite Automata and Recurrent Networks, Revisited. Entropy, 24(1), 90. https://doi.org/10.3390/e24010090





