A Probabilistic Re-Intepretation of Confidence Scores in Multi-Exit Models
Abstract
:1. Introduction
Notation
2. Deep Networks with Early Exits
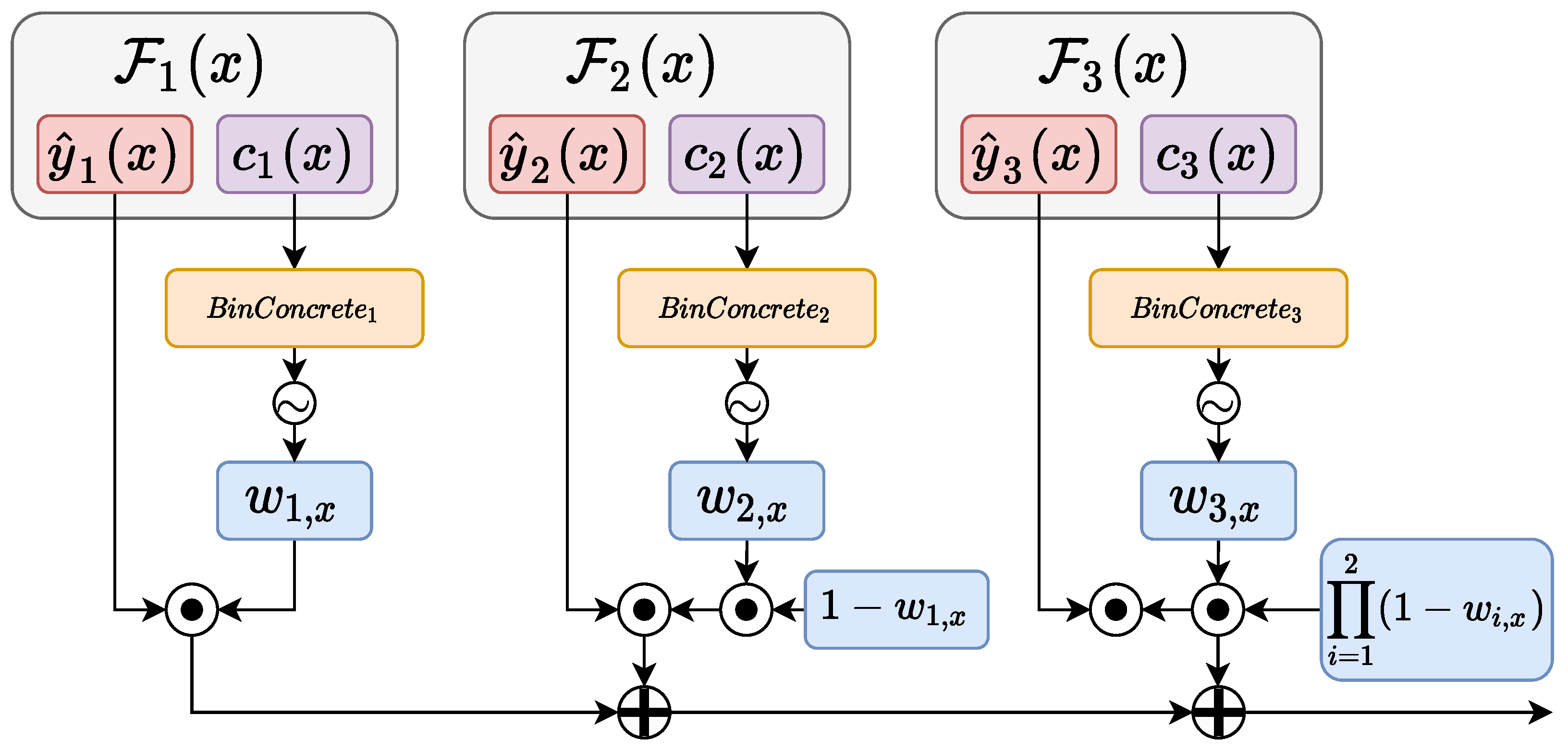
Differentiable Branching
3. Our Proposal
3.1. Regularization of the Confidence
3.2. Inference Phase
4. Experimental Evaluation
4.1. Experimental Setup
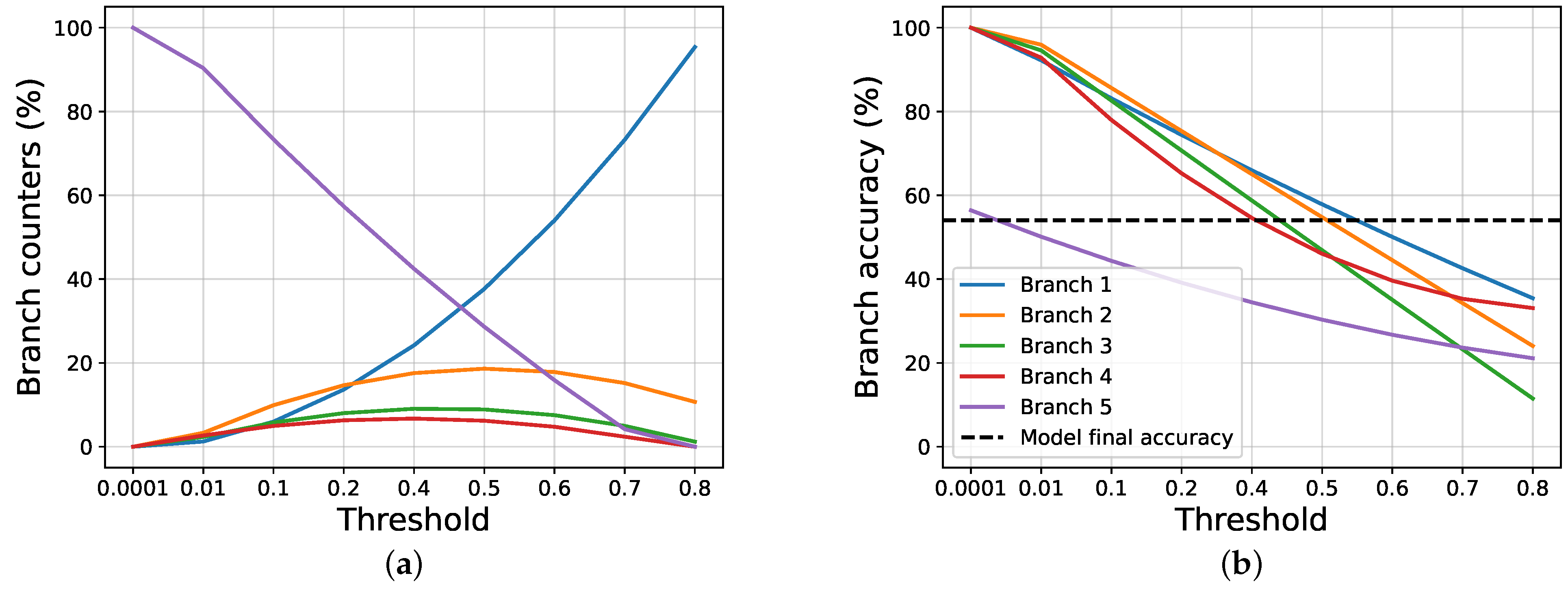
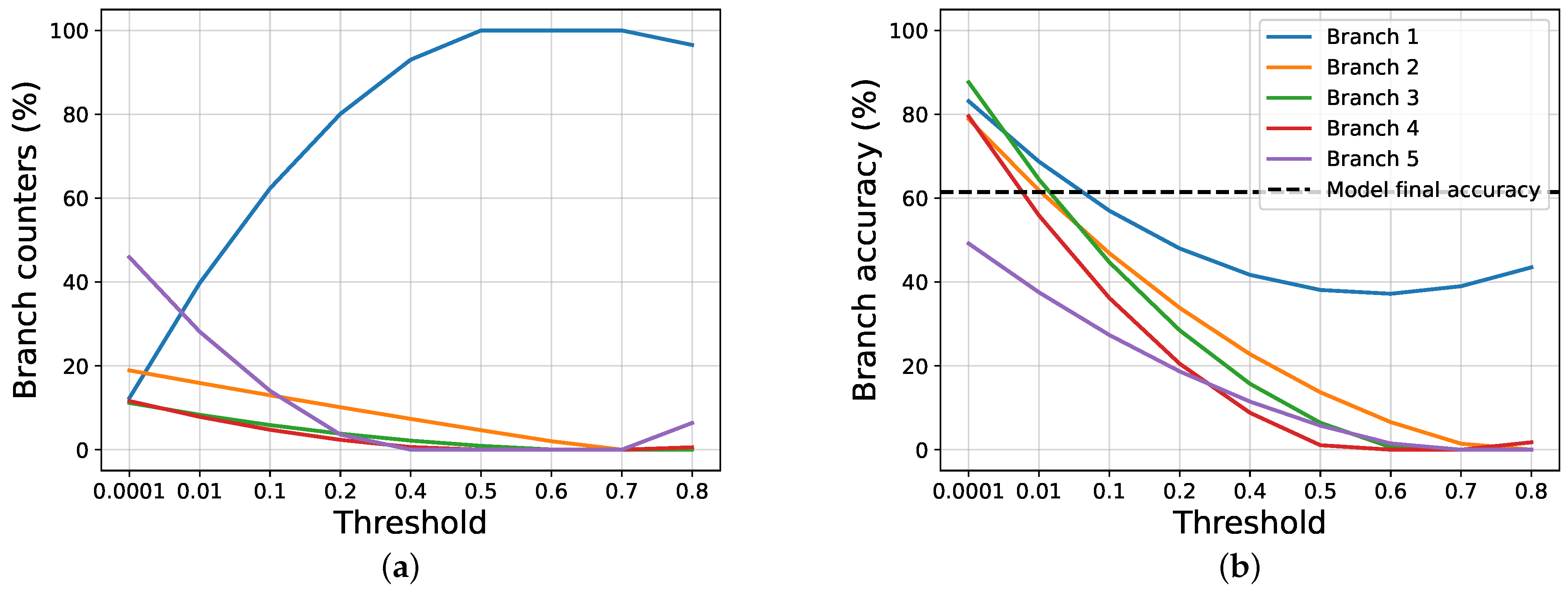
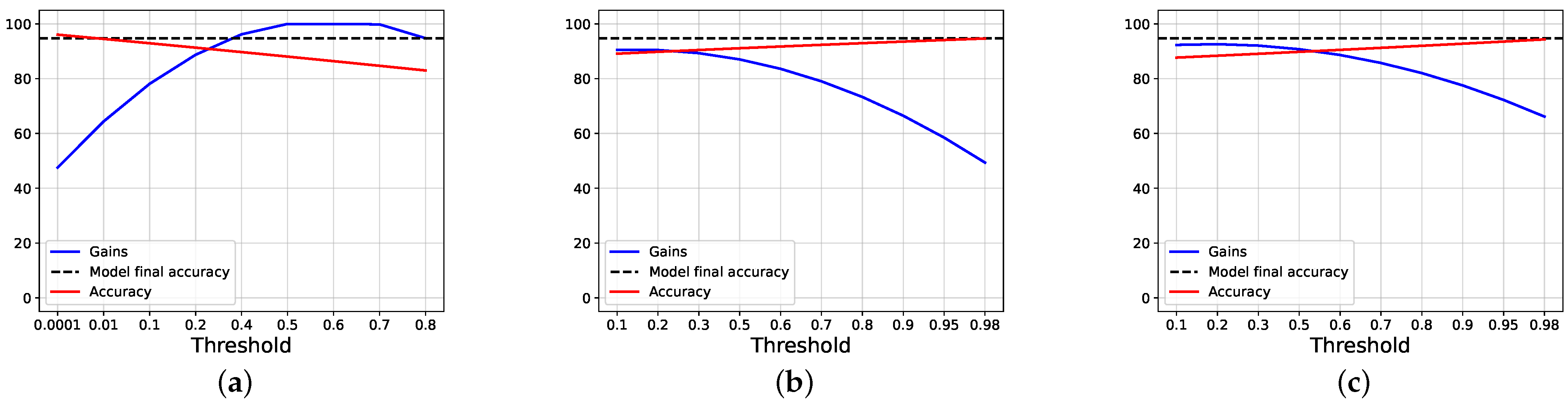
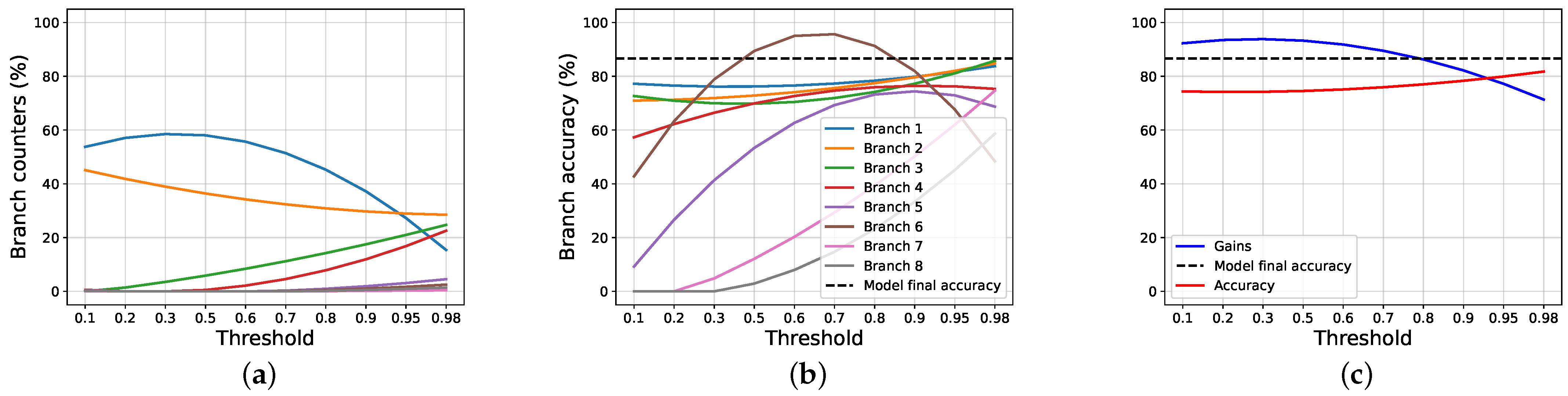
4.2. Results and Discussions
4.3. Ablation Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Shen, J. Deep visual attention prediction. IEEE Trans. Image Process. 2017, 27, 2368–2378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaya, Y.; Hong, S.; Dumitras, T. Shallow-deep networks: Understanding and mitigating network overthinking. In Proceedings of the 2019 International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 3301–3310. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Jastrzębski, S.; Kenton, Z.; Arpit, D.; Ballas, N.; Fischer, A.; Bengio, Y.; Storkey, A. Three factors influencing minima in sgd. arXiv 2017, arXiv:1711.04623. [Google Scholar]
- Huang, G.; Chen, D.; Li, T.; Wu, F.; van der Maaten, L.; Weinberger, K.Q. Multi-scale dense networks for resource efficient image classification. arXiv 2017, arXiv:1703.09844. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Wang, G.; Xie, X.; Lai, J.; Zhuo, J. Deep Growing Learning. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE Computer Society: Piscataway, NJ, USA, 2017; pp. 2831–2839. [Google Scholar]
- Marquez, E.S.; Hare, J.S.; Niranjan, M. Deep cascade learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5475–5485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belilovsky, E.; Eickenberg, M.; Oyallon, E. Greedy layerwise learning can scale to imagenet. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2019; pp. 583–593. [Google Scholar]
- Teerapittayanon, S.; McDanel, B.; Kung, H.T. Branchynet: Fast inference via early exiting from deep neural networks. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2464–2469. [Google Scholar]
- Scardapane, S.; Comminiello, D.; Scarpiniti, M.; Baccarelli, E.; Uncini, A. Differentiable branching in deep networks for fast inference. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4167–4171. [Google Scholar]
- Hua, W.; Zhou, Y.; De Sa, C.; Zhang, Z.; Suh, G.E. Channel gating neural networks. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 1886–1896. [Google Scholar]
- Lin, J.; Rao, Y.; Lu, J.; Zhou, J. Runtime Neural Pruning. Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Davis, A.; Arel, I. Low-rank approximations for conditional feedforward computation in deep neural networks. arXiv 2013, arXiv:1312.4461. [Google Scholar]
- Odena, A.; Lawson, D.; Olah, C. Changing model behavior at test-time using reinforcement learning. arXiv 2017, arXiv:1702.07780. [Google Scholar]
- Frosst, N.; Hinton, G. Distilling a neural network into a soft decision tree. arXiv 2017, arXiv:1711.09784. [Google Scholar]
- Ioannou, Y.; Robertson, D.; Zikic, D.; Kontschieder, P.; Shotton, J.; Brown, M.; Criminisi, A. Decision forests, convolutional networks and the models in-between. arXiv 2016, arXiv:1603.01250. [Google Scholar]
- Scardapane, S.; Scarpiniti, M.; Baccarelli, E.; Uncini, A. Why should we add early exits to neural networks? Cogn. Comput. 2020, 12, 954–966. [Google Scholar] [CrossRef]
- Maddison, C.; Mnih, A.; Teh, Y. The concrete distribution: A continuous relaxation of discrete random variables. In Proceedings of the International Conference on Learning Representations. International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with gumbel-softmax. arXiv 2016, arXiv:1611.01144. [Google Scholar]
- Paisley, J.W. A Simple Proof of the Stick-Breaking Construction of the Dirichlet Process; Princeton University: Princeton, NJ, USA, 2010. [Google Scholar]
- Banino, A.; Balaguer, J.; Blundell, C. Pondernet: Learning to ponder. arXiv 2021, arXiv:2107.05407. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images With Unsupervised Feature Learning. 2011. Available online: http://ufldl.stanford.edu/housenumbers/ (accessed on 17 December 2021).
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 17 December 2021).
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1389–1397. [Google Scholar]




| Dataset | AlexNet | VGG11 | ResNet20 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Baseline | Joint | Ours | Baseline | Joint | Ours | Baseline | Joint | Ours | |
| SVHN | |||||||||
| CIFAR10 | |||||||||
| CIFAR100 | |||||||||
| Method | Branch Number | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Standard | ||||||||||
| NS | ||||||||||
| NR | ||||||||||
| NR + NS | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomponi, J.; Scardapane, S.; Uncini, A. A Probabilistic Re-Intepretation of Confidence Scores in Multi-Exit Models. Entropy 2022, 24, 1. https://doi.org/10.3390/e24010001
Pomponi J, Scardapane S, Uncini A. A Probabilistic Re-Intepretation of Confidence Scores in Multi-Exit Models. Entropy. 2022; 24(1):1. https://doi.org/10.3390/e24010001
Chicago/Turabian StylePomponi, Jary, Simone Scardapane, and Aurelio Uncini. 2022. "A Probabilistic Re-Intepretation of Confidence Scores in Multi-Exit Models" Entropy 24, no. 1: 1. https://doi.org/10.3390/e24010001
APA StylePomponi, J., Scardapane, S., & Uncini, A. (2022). A Probabilistic Re-Intepretation of Confidence Scores in Multi-Exit Models. Entropy, 24(1), 1. https://doi.org/10.3390/e24010001







