Inferring Excitatory and Inhibitory Connections in Neuronal Networks
Abstract
:1. Introduction
2. Materials and Methods
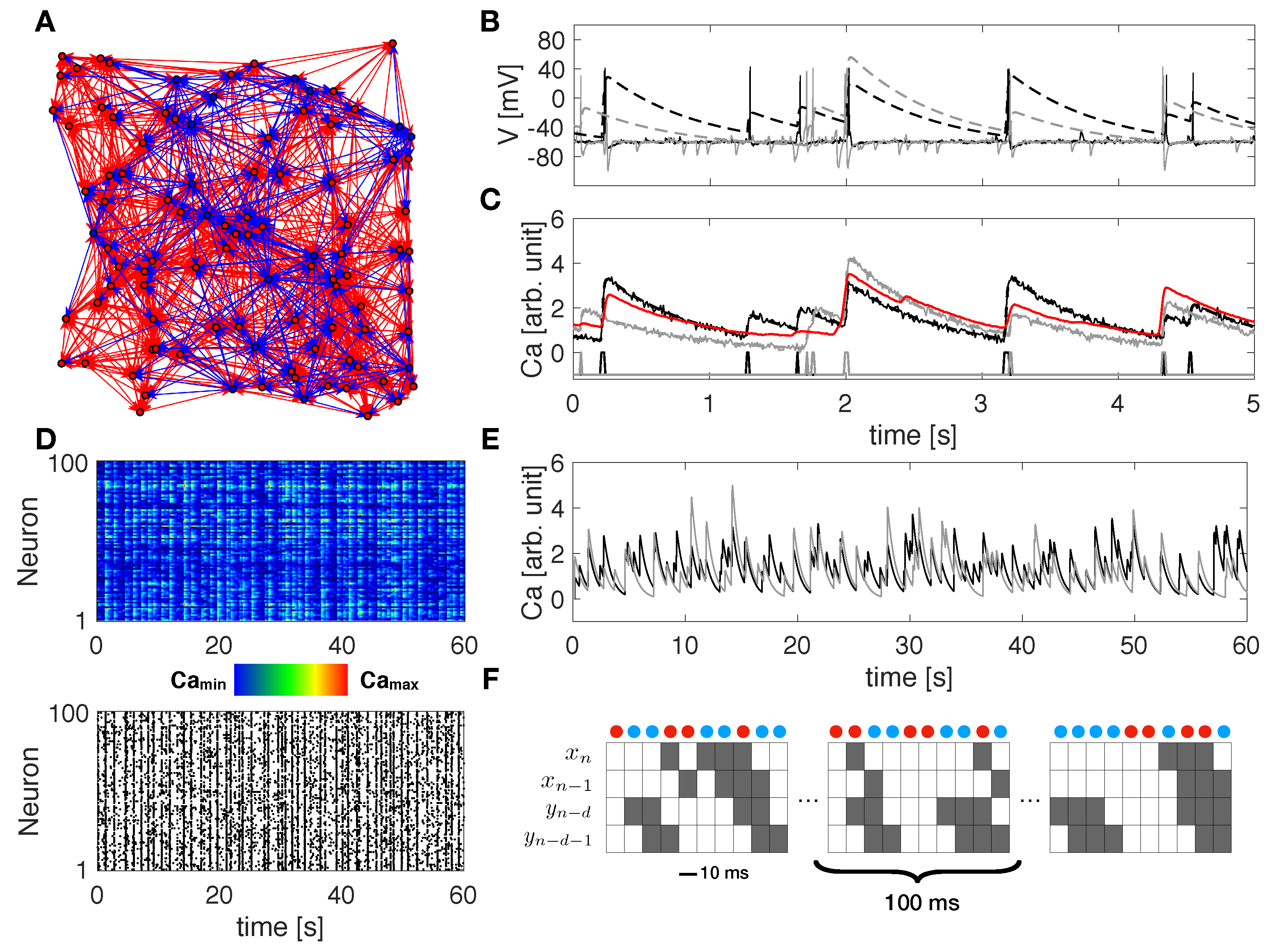
2.1. Neuronal Network Modeling
2.2. Transfer Entropy
3. Results
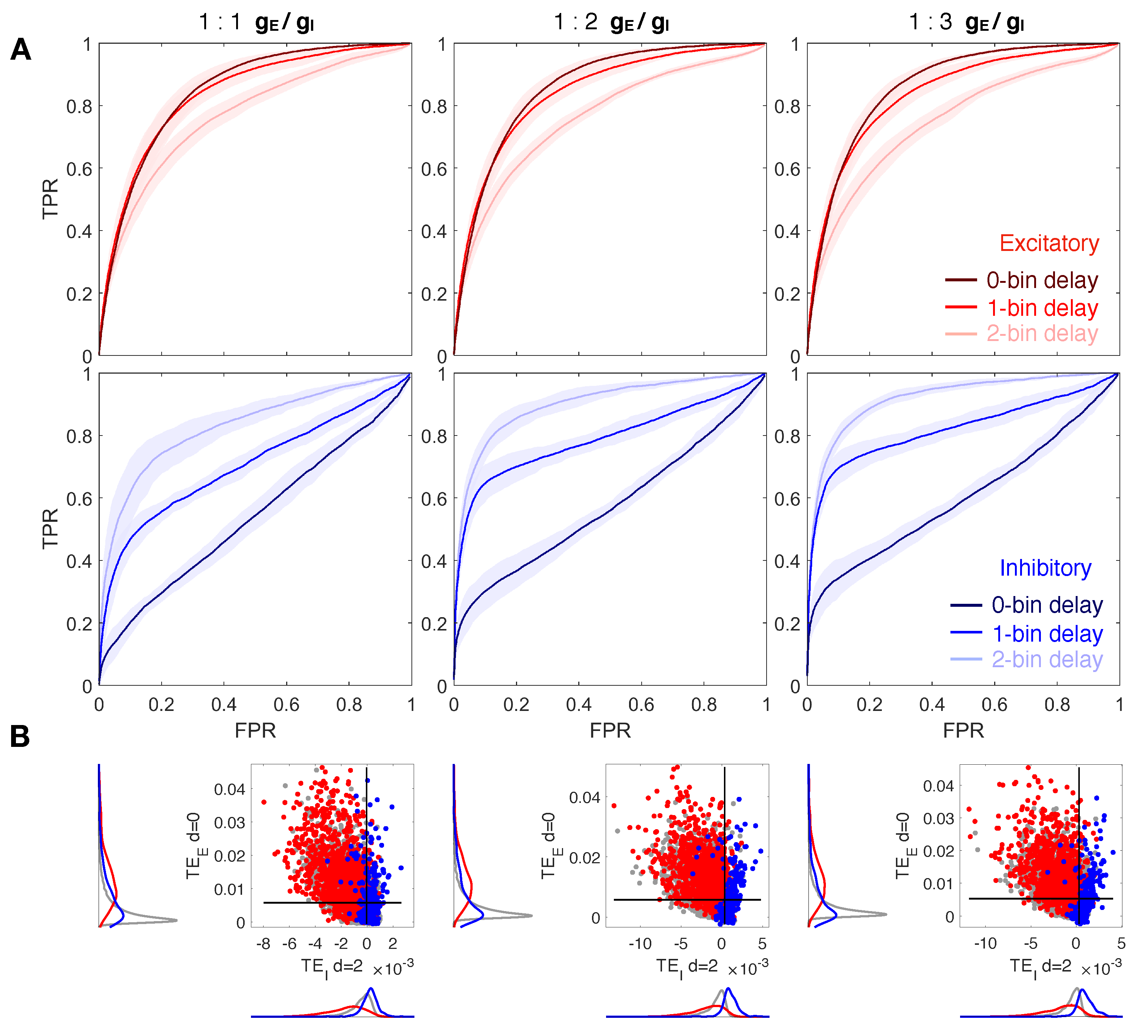
3.1. Increasing the Delay Improves Inhibitory Network Reconstruction
3.2. The Ratio Does Not Affect Network Reconstruction
3.3. Down-Sampled Bin Size Effect on Network Reconstruction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef] [Green Version]
- Avena-Koenigsberger, A.; Misic, B.; Sporns, O. Communication dynamics in complex brain networks. Nat. Rev. Neurosci. 2018, 19, 17–33. [Google Scholar] [CrossRef]
- Park, H.J.; Friston, K. Structural and functional brain networks: From connections to cognition. Science 2013, 342, 6195. [Google Scholar] [CrossRef] [Green Version]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Tibau, E.; Valencia, M.; Soriano, J. Identification of neuronal network properties from the spectral analysis of calcium imaging signals in neuronal cultures. Front. Neural Circuits 2013, 7, 199. [Google Scholar] [CrossRef]
- Gobel, W.; Helmchen, F. In Vivo calcium imaging of neural network function. Physiology 2007, 22, 358–365. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Yuste, R. In Vivo imaging of neural activity. Nat. Methods 2017, 14, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Ruz, I.D.; Schultz, S.R. Localising and classifying neurons from high density MEA recordings. J. Neurosci. Methods 2014, 233, 115–128. [Google Scholar]
- Ito, S.; Yeh, F.C.; Hiolski, E.; Rydygier, P.; Gunning, D.E.; Hottowy, P.; Timme, N.; Litke, A.M.; Beggs, J.M. Large-scale, high-resolution multielectrode-array recording depicts functional network differences of cortical and hippocampal cultures. PLoS ONE 2014, 9, e105324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Odawara, A.; Katoh, H.; Matsuda, N.; Suzuki, I. Physiological maturation and drug responses of human induced pluripotent stem cell-derived cortical neuronal networks in long-term culture. Sci. Rep. 2016, 6, 26181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eichler, M.; Dahlhaus, R.; Sandkühler, J. Partial correlation analysis for the identification of synaptic connections. Biol. Cybern. 2003, 89, 289–302. [Google Scholar] [CrossRef]
- Sheikhattar, A.; Miran, S.; Liu, J.; Fritz, J.B.; Shamma, S.A.; Kanold, P.O.; Babadi, B. Extracting neuronal functional network dynamics via adaptive Granger causality analysis. Proc. Natl. Acad. Sci. USA 2018, 115, E3869–E3878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poli, D.; Pastore, V.P.; Martinoia, S.; Massobrio, P. From functional to structural connectivity using partial correlation in neuronal assemblies. J. Neural Eng. 2016, 13, 026023. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Moran, R.; Seth, A.K. Analysing connectivity with Granger causality and dynamic causal modelling. Curr. Opin. Neurobiol. 2013, 23, 172–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stetter, O.; Battaglia, D.; Soriano, J.; Geisel, T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012, 8, e1002653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ito, S.; Hansen, M.E.; Heiland, R.; Lumsdaine, A.; Litke, A.M.; Beggs, J.M. Extending transfer entropy improves identification of effective connectivity in a spiking cortical network model. PLoS ONE 2011, 6, e27431. [Google Scholar] [CrossRef] [PubMed]
- Pastore, V.P.; Massobrio, P.; Godjoski, A.; Martinoia, S. Identification of excitatory-inhibitory links and network topology in large-scale neuronal assemblies from multi-electrode recordings. PLoS Comput. Biol. 2018, 14, e1006381. [Google Scholar] [CrossRef] [PubMed]
- Orlandi, J.G.; Stetter, O.; Soriano, J.; Geisel, T.; Battaglia, D. Transfer entropy reconstruction and labeling of neuronal connections from simulated calcium imaging. PLoS ONE 2014, 9, e98842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novelli, L.; Wollstadt, P.; Mediano, P.; Wibral, M.; Lizier, J.T. Large-scale directed network inference with multivariate transfer entropy and hierarchical statistical testing. Netw. Neurosci. 2019, 3, 827–847. [Google Scholar] [CrossRef]
- Huang, C.S.; Pal, N.R.; Chuang, C.H.; Lin, C.T. Identifying changes in EEG information transfer during drowsy driving by transfer entropy. Front. Hum. Neurosci. 2015, 9, 570. [Google Scholar] [CrossRef] [Green Version]
- Wibral, M.; Rahm, B.; Rieder, M.; Lindner, M.; Vicente, R.; Kaiser, J. Transfer entropy in magnetoencephalographic data: Quantifying information flow in cortical and cerebellar networks. Prog. Biophys. Mol. Biol. 2011, 105, 80–97. [Google Scholar] [CrossRef]
- Kajiwara, M.; Nomura, R.; Goetze, F.; Kawabata, M.; Isomura, Y.; Akutsu, T.; Shimono, M. Inhibitory neurons exhibit high controlling ability in the cortical microconnectome. PLoS Comput. Biol. 2021, 17, e1008846. [Google Scholar] [CrossRef] [PubMed]
- Brunel, N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000, 8, 183–208. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Lacalle, E.; Moses, E. Slow and fast pulses in 1-D cultures of excitatory neurons. J. Comput. Neurosci. 2009, 26, 475–493. [Google Scholar] [CrossRef] [PubMed]
- Orlandi, J.G.; Soriano, J.; Alvarez-Lacalle, E.; Teller, S.; Casademunt, J. Noise focusing and the emergence of coherent activity in neuronal cultures. Nat. Phys. 2013, 9, 582–590. [Google Scholar] [CrossRef]
- Markram, H.; Lübke, J.; Frotscher, M.; Roth, A.; Sakmann, B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J. Physiol. 1997, 500, 409–440. [Google Scholar] [CrossRef]
- Thomson, A.M.; West, D.C.; Wang, Y.; Bannister, A.P. Synaptic connections and small circuits involving excitatory and inhibitory neurons in layers 2–5 of adult rat and cat neocortex: Triple intracellular recordings and biocytin labelling in vitro. Cereb. Cortex 2002, 12, 936–953. [Google Scholar] [CrossRef] [Green Version]
- Holmgren, C.; Harkany, T.; Svennenfors, B.; Zilberter, Y. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J. Physiol. 2003, 551, 139–153. [Google Scholar] [CrossRef]
- Soriano, J.; Martínez, M.R.; Tlusty, T.; Moses, E. Development of input connections in neural cultures. Proc. Natl. Acad. Sci. USA 2008, 105, 13758–13763. [Google Scholar] [CrossRef] [Green Version]
- Kerr, J.N.; Greenberg, D.; Helmchen, F. Imaging input and output of neocortical networks in vivo. Proc. Natl. Acad. Sci. USA 2005, 102, 14063–14068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grewe, B.F.; Langer, D.; Kasper, H.; Kampa, B.M.; Helmchen, F. High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nat. Methods 2010, 7, 399–405. [Google Scholar] [CrossRef] [PubMed]
- Palazzolo, G.; Moroni, M.; Soloperto, A.; Aletti, G.; Naldi, G.; Vassalli, M.; Nieus, T.; Difato, F. Fast wide-volume functional imaging of engineered in vitro brain tissues. Sci. Rep. 2017, 7, 8499. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [Green Version]
- MacKay, D.J.; Mac Kay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wollstadt, P.; Martínez-Zarzuela, M.; Vicente, R.; Díaz-Pernas, F.J.; Wibral, M. Efficient transfer entropy analysis of non-stationary neural time series. PLoS ONE 2014, 9, e102833. [Google Scholar] [CrossRef] [Green Version]
- Shovon, M.H.I.; Nandagopal, N.; Vijayalakshmi, R.; Du, J.T.; Cocks, B. Directed connectivity analysis of functional brain networks during cognitive activity using transfer entropy. Neural Process. Lett. 2017, 45, 807–824. [Google Scholar] [CrossRef]
- Thivierge, J.P. Scale-free and economical features of functional connectivity in neuronal networks. Phys. Rev. E 2014, 90, 022721. [Google Scholar] [CrossRef] [PubMed]
- Shimono, M.; Beggs, J.M. Functional clusters, hubs, and communities in the cortical microconnectome. Cereb. Cortex 2015, 25, 3743–3757. [Google Scholar] [CrossRef] [Green Version]
- Isaacson, J.S.; Scanziani, M. How inhibition shapes cortical activity. Neuron 2011, 72, 231–243. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Vives, M.V.; Mattia, M.; Compte, A.; Perez-Zabalza, M.; Winograd, M.; Descalzo, V.F.; Reig, R. Inhibitory modulation of cortical up states. J. Neurophysiol. 2010, 104, 1314–1324. [Google Scholar] [CrossRef]
- Tahvildari, B.; Wölfel, M.; Duque, A.; McCormick, D.A. Selective functional interactions between excitatory and inhibitory cortical neurons and differential contribution to persistent activity of the slow oscillation. J. Neurosci. 2012, 32, 12165–12179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogels, T.P.; Sprekeler, H.; Zenke, F.; Clopath, C.; Gerstner, W. Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science 2011, 334, 1569–1573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [Green Version]
- Dunning, D.; Hoover, C.; Soltesz, I.; Smith, M.; O’Dowd, D.K. GABAA receptor–mediated miniature postsynaptic currents and α-subunit expression in developing cortical neurons. J. Neurophysiol. 1999, 82, 3286–3297. [Google Scholar] [CrossRef] [PubMed]
- Ropert, N.; Miles, R.; Korn, H. Characteristics of miniature inhibitory postsynaptic currents in CA1 pyramidal neurones of rat hippocampus. J. Physiol. 1990, 428, 707–722. [Google Scholar] [CrossRef] [Green Version]
- Collingridge, G.L.; Gage, P.W.; Robertson, B. Inhibitory post-synaptic currents in rat hippocampal CA1 neurones. J. Physiol. 1984, 356, 551–564. [Google Scholar] [CrossRef]
- Xiang, Z.; Huguenard, J.R.; Prince, D.A. GABAA receptor-mediated currents in interneurons and pyramidal cells of rat visual cortex. J. Physiol. 1998, 506, 715–730. [Google Scholar] [CrossRef] [PubMed]
- Gardner, D. Variations in amplitude and time course of inhibitory postsynaptic currents. J. Neurophysiol. 1986, 56, 1424–1438. [Google Scholar] [CrossRef]
- Liu, G.; Choi, S.; Tsien, R.W. Variability of neurotransmitter concentration and nonsaturation of postsynaptic AMPA receptors at synapses in hippocampal cultures and slices. Neuron 1999, 22, 395–409. [Google Scholar] [CrossRef] [Green Version]
- Wyllie, D.J.; Manabe, T.; Nicoll, R.A. A rise in postsynaptic Ca2+ potentiates miniature excitatory postsynaptic currents and AMPA responses in hippocampal neurons. Neuron 1994, 12, 127–138. [Google Scholar] [CrossRef]
- Sah, P.; Hestrin, S.; Nicoll, R. Properties of excitatory postsynaptic currents recorded in vitro from rat hippocampal interneurones. J. Physiol. 1990, 430, 605–616. [Google Scholar] [CrossRef]
- Pospischil, M.; Toledo-Rodriguez, M.; Monier, C.; Piwkowska, Z.; Bal, T.; Frégnac, Y.; Markram, H.; Destexhe, A. Minimal Hodgkin–Huxley type models for different classes of cortical and thalamic neurons. Biol. Cybern. 2008, 99, 427–441. [Google Scholar] [CrossRef]
- Nicoletti, M.; Loppini, A.; Chiodo, L.; Folli, V.; Ruocco, G.; Filippi, S. Biophysical modeling of C. elegans neurons: Single ion currents and whole-cell dynamics of AWCon and RMD. PLoS ONE 2019, 14, e0218738. [Google Scholar] [CrossRef]
- Esser, S.K.; Hill, S.L.; Tononi, G. Modeling the effects of transcranial magnetic stimulation on cortical circuits. J. Neurophysiol. 2005, 94, 622–639. [Google Scholar] [CrossRef] [Green Version]
- Rusu, C.V.; Murakami, M.; Ziemann, U.; Triesch, J. A model of TMS-induced I-waves in motor cortex. Brain Stimul. 2014, 7, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Louis, S.G.; Gerstein, G.L.; Grün, S.; Diesmann, M. Surrogate spike train generation through dithering in operational time. Front. Comput. Neurosci. 2010, 4, 127. [Google Scholar] [CrossRef] [Green Version]
- Timme, N.M.; Lapish, C. A tutorial for information theory in neuroscience. eNeuro 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Grun, S. Data-driven significance estimation for precise spike correlation. J. Neurophysiol. 2009, 101, 1126–1140. [Google Scholar] [CrossRef] [Green Version]
- Harmah, D.J.; Li, C.; Li, F.; Liao, Y.; Wang, J.; Ayedh, W.; Bore, J.C.; Yao, D.; Dong, W.; Xu, P. Measuring the non-linear directed information flow in schizophrenia by multivariate transfer entropy. Front. Comput. Neurosci. 2020, 13, 85. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Huang, L.; Cai, S.; Zhang, Y.; von Deneen, K.M.; Ren, A.; Ren, J. Altered effective connectivity patterns of the default mode network in Alzheimer’s disease: An fMRI study. Neurosci. Lett. 2014, 578, 171–175. [Google Scholar] [CrossRef] [PubMed]
- Inman, C.S.; James, G.A.; Hamann, S.; Rajendra, J.K.; Pagnoni, G.; Butler, A.J. Altered resting-state effective connectivity of fronto-parietal motor control systems on the primary motor network following stroke. Neuroimage 2012, 59, 227–237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.Y.; Wang, J.; Zhou, J.; Guan, Y.G.; Zhai, F.; Liu, C.Q.; Xu, F.F.; Han, Y.X.; Yan, Z.F.; Luan, G.M. Identification of the epileptogenic zone of temporal lobe epilepsy from stereo-electroencephalography signals: A phase transfer entropy and graph theory approach. Neuroimage Clin. 2017, 16, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Parker, C.S.; Clayden, J.D.; Cardoso, M.J.; Rodionov, R.; Duncan, J.S.; Scott, C.; Diehl, B.; Ourselin, S. Structural and effective connectivity in focal epilepsy. Neuroimage Clin. 2018, 17, 943–952. [Google Scholar] [CrossRef] [PubMed]


| Deterministic [bin 10 ms, 1:2] | Noise [bin 10 ms, 1:2] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | I | E | I | |||||||||
| 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | |
| AUC | 0.86 | 0.84 | 0.76 | 0.58 | 0.79 | 0.90 | 0.86 | 0.84 | 0.76 | 0.58 | 0.76 | 0.89 |
| J | 0.57 | 0.54 | 0.41 | 0.21 | 0.55 | 0.68 | 0.57 | 0.54 | 0.41 | 0.19 | 0.46 | 0.65 |
| Sens | 0.83 | 0.76 | 0.63 | 0.30 | 0.65 | 0.81 | 0.83 | 0.79 | 0.68 | 0.29 | 0.57 | 0.80 |
| Spec | 0.75 | 0.79 | 0.78 | 0.91 | 0.90 | 0.87 | 0.74 | 0.76 | 0.73 | 0.90 | 0.89 | 0.84 |
| Deterministic [bin 10 ms, 1:1] | Deterministic (bin 10 ms, 1:3] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | I | E | I | |||||||||
| 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | |
| AUC | 0.84 | 0.84 | 0.76 | 0.54 | 0.71 | 0.83 | 0.86 | 0.84 | 0.75 | 0.60 | 0.82 | 0.92 |
| J | 0.55 | 0.54 | 0.42 | 0.12 | 0.39 | 0.56 | 0.58 | 0.54 | 0.39 | 0.26 | 0.60 | 0.71 |
| Sens | 0.82 | 0.79 | 0.67 | 0.32 | 0.53 | 0.72 | 0.83 | 0.75 | 0.64 | 0.33 | 0.69 | 0.85 |
| Spec | 0.73 | 0.75 | 0.75 | 0.80 | 0.86 | 0.84 | 0.75 | 0.79 | 0.75 | 0.93 | 0.91 | 0.86 |
| Deterministic [bin 5 ms, 1:2] | Deterministic (bin 20 ms, 1:2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | I | E | I | |||||||||
| 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | |
| AUC | 0.84 | 0.83 | 0.81 | 0.59 | 0.71 | 0.81 | 0.87 | 0.81 | 0.58 | 0.54 | 0.84 | 0.78 |
| J | 0.54 | 0.54 | 0.50 | 0.27 | 0.46 | 0.59 | 0.61 | 0.48 | 0.13 | 0.10 | 0.57 | 0.42 |
| Sens | 0.82 | 0.79 | 0.74 | 0.34 | 0.56 | 0.72 | 0.85 | 0.74 | 0.51 | 0.31 | 0.71 | 0.69 |
| Spec | 0.72 | 0.75 | 0.77 | 0.93 | 0.90 | 0.88 | 0.76 | 0.75 | 0.62 | 0.79 | 0.86 | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghirga, S.; Chiodo, L.; Marrocchio, R.; Orlandi, J.G.; Loppini, A. Inferring Excitatory and Inhibitory Connections in Neuronal Networks. Entropy 2021, 23, 1185. https://doi.org/10.3390/e23091185
Ghirga S, Chiodo L, Marrocchio R, Orlandi JG, Loppini A. Inferring Excitatory and Inhibitory Connections in Neuronal Networks. Entropy. 2021; 23(9):1185. https://doi.org/10.3390/e23091185
Chicago/Turabian StyleGhirga, Silvia, Letizia Chiodo, Riccardo Marrocchio, Javier G. Orlandi, and Alessandro Loppini. 2021. "Inferring Excitatory and Inhibitory Connections in Neuronal Networks" Entropy 23, no. 9: 1185. https://doi.org/10.3390/e23091185
APA StyleGhirga, S., Chiodo, L., Marrocchio, R., Orlandi, J. G., & Loppini, A. (2021). Inferring Excitatory and Inhibitory Connections in Neuronal Networks. Entropy, 23(9), 1185. https://doi.org/10.3390/e23091185







