Observer Based Multi-Level Fault Reconstruction for Interconnected Systems
Abstract
:1. Introduction
2. Model Description and Problem Formulation
3. On Condition of Fault Reconstructability Locally and Globally
3.1. Fault Reconstructability Condition
3.2. Minimum Number of Measurements and Reconstructable Unknown Inputs
4. Observer Design for Unknown Input Reconstruction
4.1. Asymptotic Reduced-Order Observer Design with Auxiliary Output
4.2. Auxiliary Output Estimation
4.3. Reconstruction of the Unknown Inputs by Asymptotic Reduced-Order Observer with Auxiliary Output
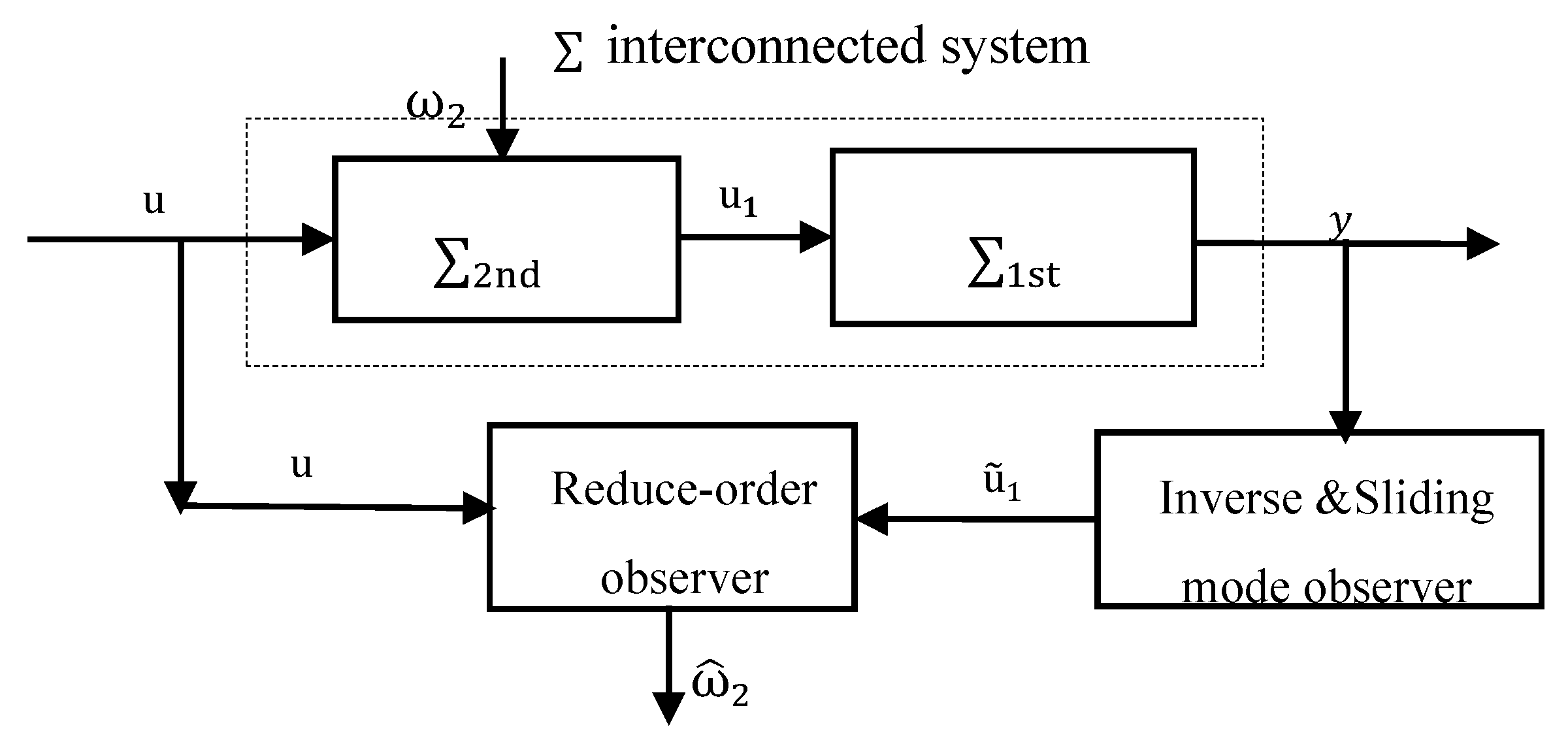
5. Numerical Simulation Implementation on a Pilot Intensified Heat Exchanger
5.1. Interconnected System Modelling
5.2. Observer Design for Unknown Input Reconstruction
5.2.1. Reduce-Order Observer Design
5.2.2. System Inversion Based Interconnection Reconstruction
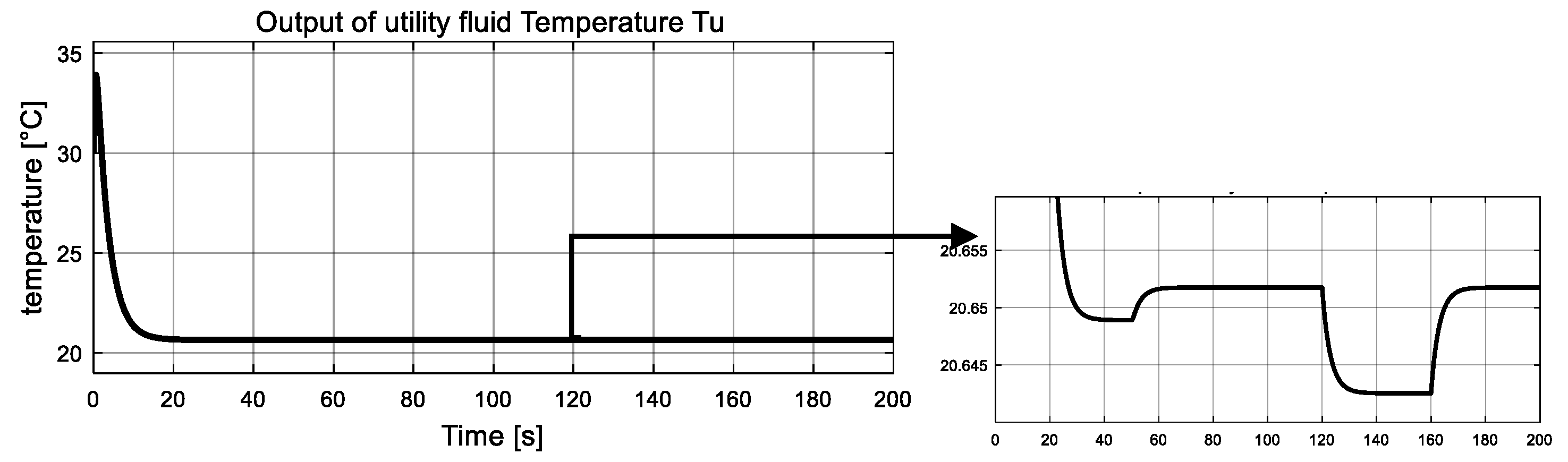
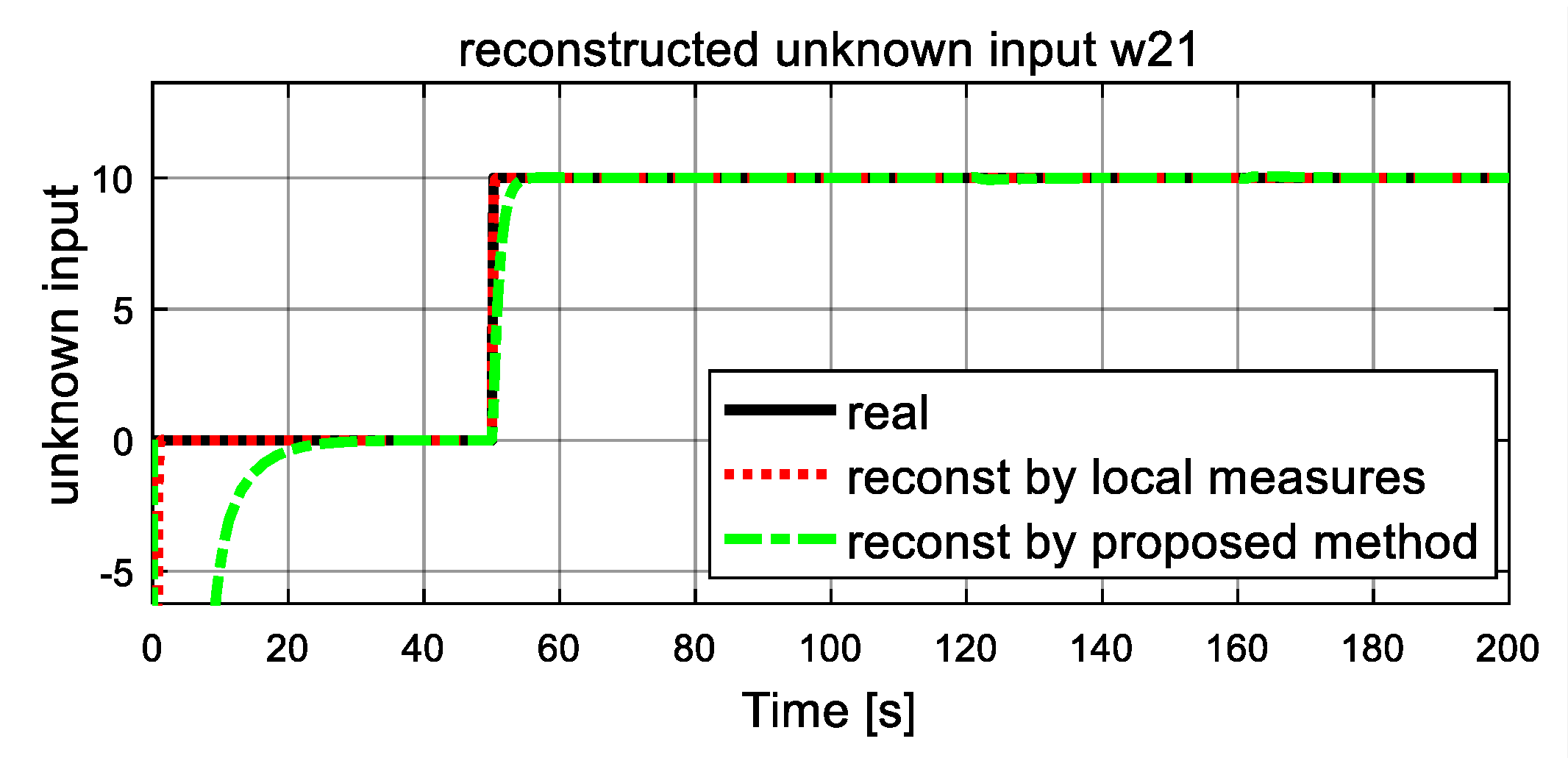
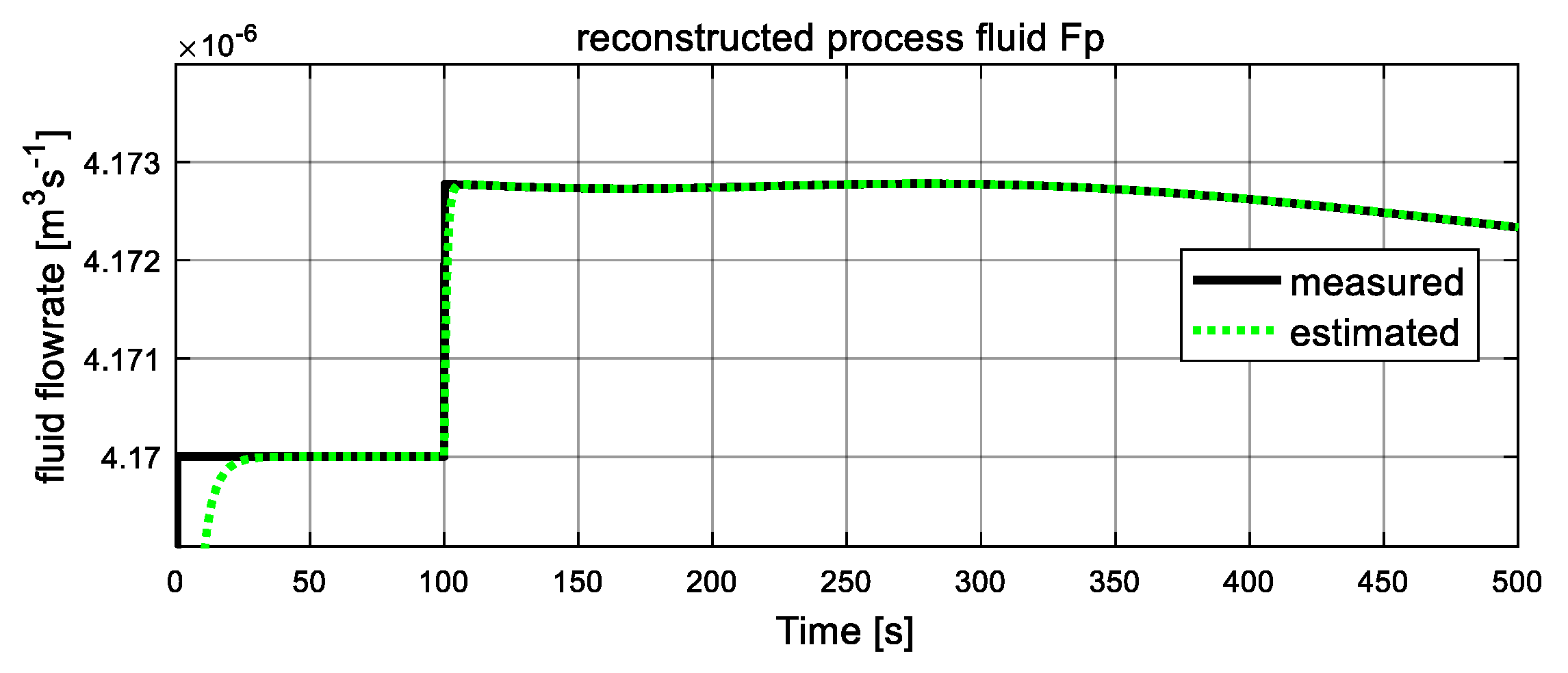
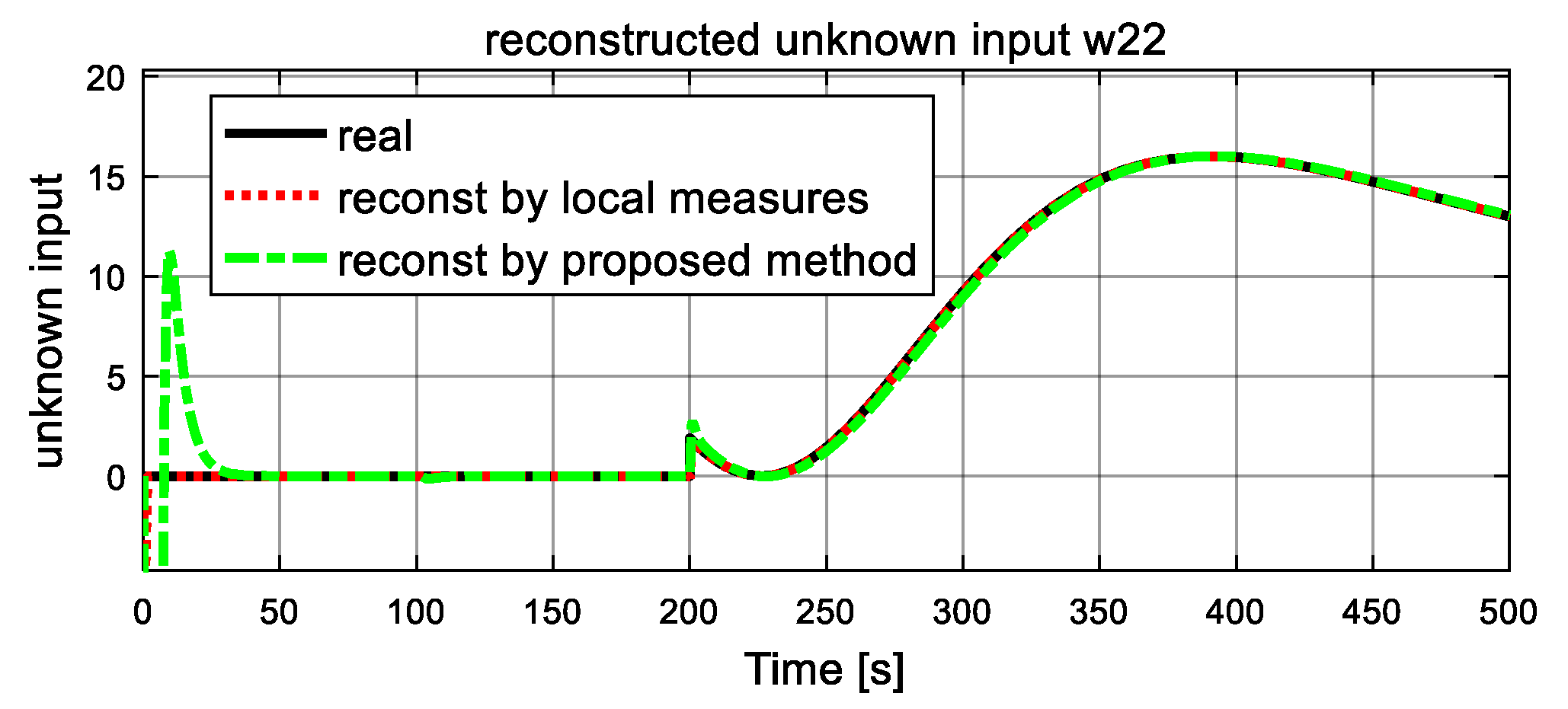
5.3. Simulation Results and Discussion
6. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Ding, S.X. Model-Based Fault Diagnosis Techniques-Design Schemes, Algorithms, and Tools; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques Part II: Fault Diagnosis with Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 1. [Google Scholar] [CrossRef] [Green Version]
- Mironova, A.; Mercorelli, P.; Zedler, A. A multi input sliding mode control for Peltier Cells using a cold–hot sliding surface. J. Frankl. Inst. 2018, 355, 9351–9373. [Google Scholar] [CrossRef]
- Traoré, D.; Leon, J.D.; Glumineau, A. Adaptive Interconnected Observer-Based Backstepping Control Design For Sen-sorless PMSM. Automatica 2012, 48, 682–687. [Google Scholar] [CrossRef]
- Jia, Q.; Wu, L.; Li, H. Robust Actuator Fault Reconstruction for Takagi-Sugeno Fuzzy Systems with Time-varying Delays via a Synthesized Learning and Luenberger Observer. Int. J. Control Autom. Syst. 2021, 19, 799–809. [Google Scholar] [CrossRef]
- Yan, X.-G.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Jia, Q.; Chen, W.; Zhang, Y.; Li, H. Fault reconstruction for continuous-time systems via learning observers. Asian J. Control 2014, 18, 549–561. [Google Scholar] [CrossRef]
- Vijay, P.; Tadé, M.O.; Ahmed, K.; Utikar, R.; Pareek, V. Simultaneous estimation of states and inputs in a planar solid oxide fuel cell using nonlinear adaptive observer design. J. Power Sources 2014, 248, 1218–1233. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.C.L.; Lee, T.H.; Tan, C.P.; Trinh, H.; Park, J.H. A Nonlinear Observer for Robust Fault Reconstruction in One-Sided Lipschitz and Quadratically Inner-Bounded Nonlinear Descriptor Systems. IEEE Access 2021, 9, 22455–22469. [Google Scholar] [CrossRef]
- De Persis, C.; Isidori, A. A geometric approach to nonlinear fault detection and isolation. IEEE Trans. Automat. Control 2001, 46, 853–865. [Google Scholar] [CrossRef] [Green Version]
- Edelmayer, A.; Bokor, J.; Szabo, Z.; Szigeti, F. Input reconstruction by means of system inversion: A geometric approach to fault detection and isolation in nonlinear systems. Int. J. Appl. Math. Comput. Sci. 2004, 14, 189–199. [Google Scholar]
- Fang, H.; De Callafon, R.A.; Cortes, J. Simultaneous input and state estimation for nonlinear systems with applications to flow field estimation. Automatica 2013, 49, 2805–2812. [Google Scholar] [CrossRef]
- Pan, S.; Xiao, D.; Xing, S.; Law, S.; Du, P.; Li, Y. A general extended Kalman filter for simultaneous estimation of system and unknown inputs. Eng. Struct. 2016, 109, 85–98. [Google Scholar] [CrossRef]
- Hou, M.; Patton, R. Input Observability and Input Reconstruction. Automatica 1998, 34, 789–794. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Corlessb, M. Estimating unbounded unknown inputs in nonlinear systems. Automatica 2019, 104, 57–66. [Google Scholar] [CrossRef]
- Martínez-Guerra, R.; Mata-Machuca, J.; Rincón-Pasaye, J. Fault diagnosis viewed as a left invertibility problem. ISA Trans. 2013, 52, 652–661. [Google Scholar] [CrossRef]
- Li, J.; Raïssi, T.; Wang, Z.H.; Wang, X.S.; Shen, Y. Interval estimation of state and unknown input for linear discrete-time systems. J. Frankl. Inst. 2020, 357, 9045–9062. [Google Scholar] [CrossRef]
- Illonetto, G.; Saccomani, M.P. Input estimation in nonlinear dynamical systems using differential algebra techniques. Automatica 2006, 42, 2117–2129. [Google Scholar] [CrossRef]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X.G. Higher-order sliding-mode observer for state estimation and input reconstruction in nonlinear systems. Int. J. Robust Nonlinear Control 2008, 18, 399–412. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Sundaram, S.; Corless, M.J.; Buzzard, G.T.; Rundell, A.E.; Zak, S.H. Distributed Unknown Input Observers For Interconnected Nonlinear Systems. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 101–106. [Google Scholar]
- Dashkovskiy, S.; Naujok, L. Quasi-ISS/ISDS observers for interconnected systems and applications. Syst. Control Lett. 2015, 77, 11–21. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, F.; Yu, K.; Bu, X. Observer-based state estimation and unknown input reconstruction for nonlinear complex dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 927–939. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.-M.; Chen, X.-P.; Dahhou, B.; Li, Z.-T. Observer Design for Nonlinear Invertible System from the View of Both Local and Global Levels. Appl. Sci. 2020, 10, 7966. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, X. A distributed detection scheme for process faults and sensor faults in a class of interconnected nonlinear uncertain systems. In Proceedings of the Decision and Control (CDC), 2012 IEEE 51st Annual Conference, Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Hamida, M.A.; Leon, J.D.; Glumineau, A.; Boisliveau, R. An adaptive interconnected observer for sensorless control of PM synchronous motors with online parameter identification. IEEE Trans. Ind. Electron. 2013, 60, 739–748. [Google Scholar] [CrossRef]
- Keliris, C.; Polycarpou, M.M.; Parisini, T. Distributed fault diagnosis for process and sensor faults in a class of interconnected input–output nonlinear discrete-time systems. Int. J. Control 2015, 88, 1472–1489. [Google Scholar] [CrossRef] [Green Version]
- Ali, H.S.; Alma, M.; Darouach, M. Controllers design for two interconnected systems via unbiased observers. IFAC Proc. Vol. 2014, 47, 10808–10813. [Google Scholar] [CrossRef] [Green Version]
- Xi, X.; Zhao, J.; Liu, T.; Yan, L. Distributed-observer-based fault diagnosis and fault-tolerant control for time-varying discrete interconnected systems. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 459–482. [Google Scholar] [CrossRef]
- Methnani, S.; Gauthier, J.P.; Lafont, F. Sensor fault reconstruction and observability for unknown inputs, with an application to wastewater treatment plants. Int. J. Control 2011, 84, 822–833. [Google Scholar] [CrossRef]
- Zhang, M.; Dahhou, B.; Li, Z.T. On Invertibility of an Interconnected System Composed of Two Dynamic Subsystems. Appl. Sci. 2021, 11, 596. [Google Scholar] [CrossRef]
- Indra, S.; Travé-Massuyès, L.; Chanthery, E. A decentralized fault detection and isolation scheme for spacecraft: Bridging the gap between model-based fault detection and isolation research and practice. EDP Sci. 2013, 6, 281–298. [Google Scholar]
- Boem, F.; Ferrari, R.M.; Parisini, T. Distributed Fault Detection and Isolation of Continuous-Time Non-Linear Systems. Eur. J. Control 2011, 17, 603–620. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.T.; Cabassud, M.; Dahhou, B.E. Root cause analysis of actuator fault based on invertibility of interconnected system. Int. J. Model. Identif. Control 2017, 27, 256–270. [Google Scholar] [CrossRef] [Green Version]
- Ng, M.K.Y.; Tan, C.P.; Oetomo, D. Disturbance decoupled fault reconstruction using cascaded sliding mode observers. Automatica 2012, 48, 794–799. [Google Scholar] [CrossRef]
- Lendek, Z.; Babuška, R.; De Schutter, B. Distributed Kalman filtering for cascaded systems. Eng. Appl. Artif. Intell. 2008, 21, 457–469. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Mercorelli, P. Global finite-time stabilization of planar linear systems with actuator saturation. IEEE Trans. Circuits Syst. II Express Briefs 2016, 64, 947–951. [Google Scholar] [CrossRef]
- Benmansour, K.; Tlemani, A.; Djemai, M.; De Leon, J. A new interconnected observer design in power converter: Theory and experimentation. Nonlinear Dyn. Syst. Theory 2010, 10, 211–224. [Google Scholar]
- Bartyś, M.; Patton, R.; Syfert, M.; Heras, S.D.L.; Quevedo, J. Introduction to the DAMADICS actuator FDI benchmark study. Control Eng. Pract. 2006, 14, 577–596. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Toubakh, H.; Ouladsine, M. Fault prognosis based on fault reconstruction: Application to a mechatronic system. In Proceedings of the 3rd International Conference on Systems and Control, Algiers, Algeria, 29–31 October 2013; pp. 383–388. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Dahhou, B.; Wu, Q.; Li, Z. Observer Based Multi-Level Fault Reconstruction for Interconnected Systems. Entropy 2021, 23, 1102. https://doi.org/10.3390/e23091102
Zhang M, Dahhou B, Wu Q, Li Z. Observer Based Multi-Level Fault Reconstruction for Interconnected Systems. Entropy. 2021; 23(9):1102. https://doi.org/10.3390/e23091102
Chicago/Turabian StyleZhang, Mei, Boutaïeb Dahhou, Qinmu Wu, and Zetao Li. 2021. "Observer Based Multi-Level Fault Reconstruction for Interconnected Systems" Entropy 23, no. 9: 1102. https://doi.org/10.3390/e23091102
APA StyleZhang, M., Dahhou, B., Wu, Q., & Li, Z. (2021). Observer Based Multi-Level Fault Reconstruction for Interconnected Systems. Entropy, 23(9), 1102. https://doi.org/10.3390/e23091102




