Robust Stabilization and Synchronization of a Novel Chaotic System with Input Saturation Constraints
Abstract
1. Introduction
2. Related Work
3. Definition of the Novel Chaotic System
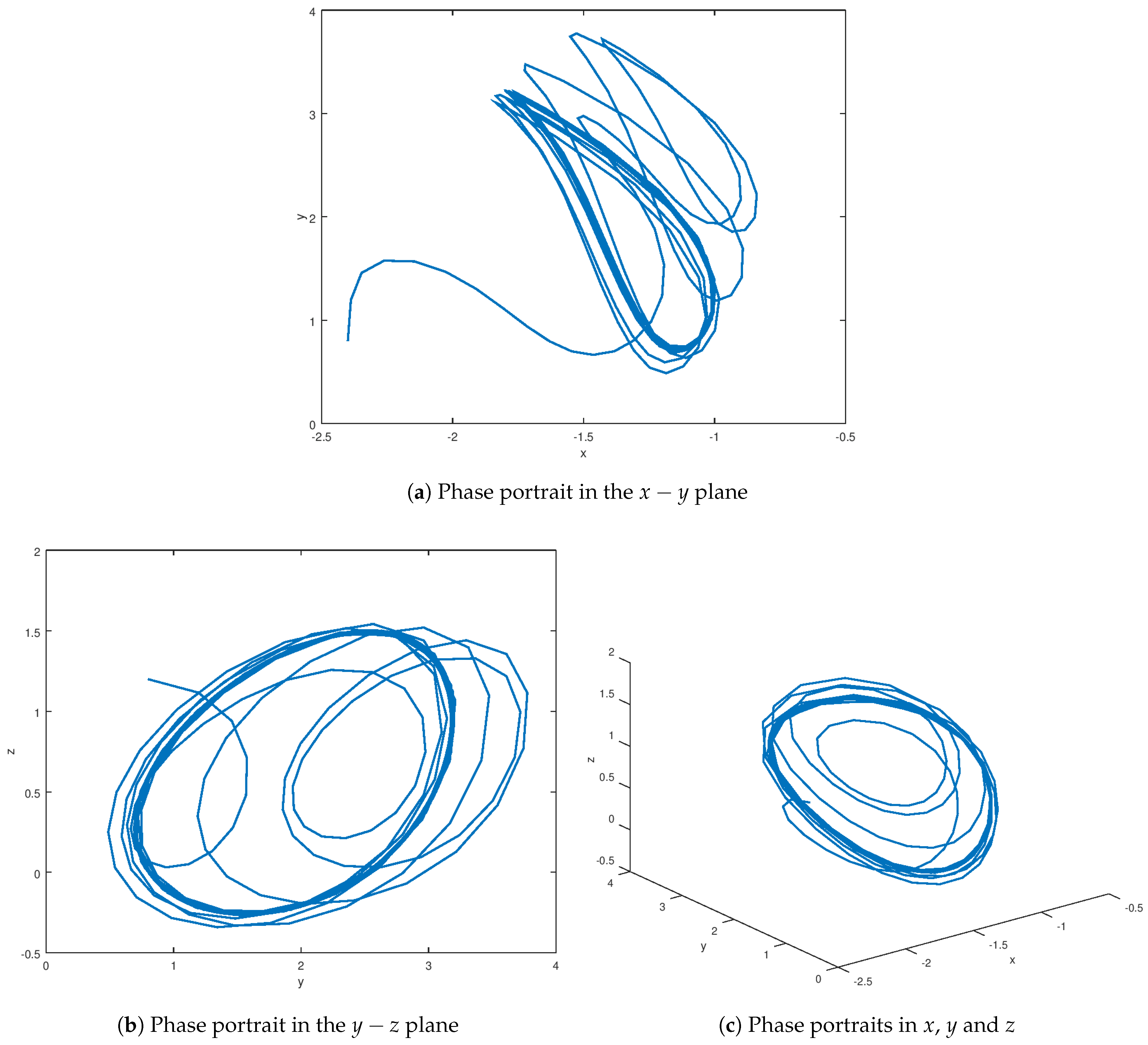
3.1. Definition of the Novel Chaotic System
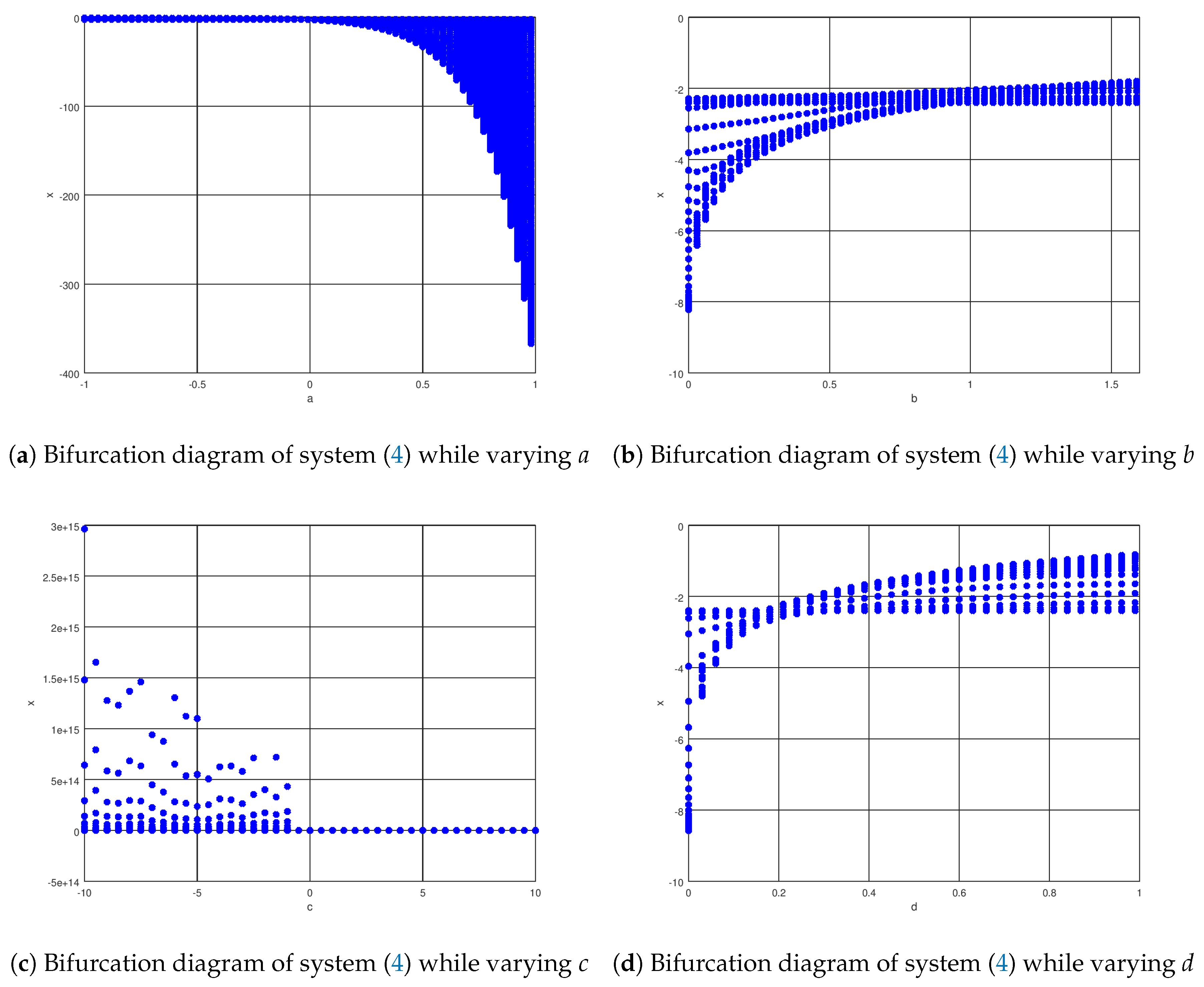
3.2. Bifurcation Analysis
4. Main Results
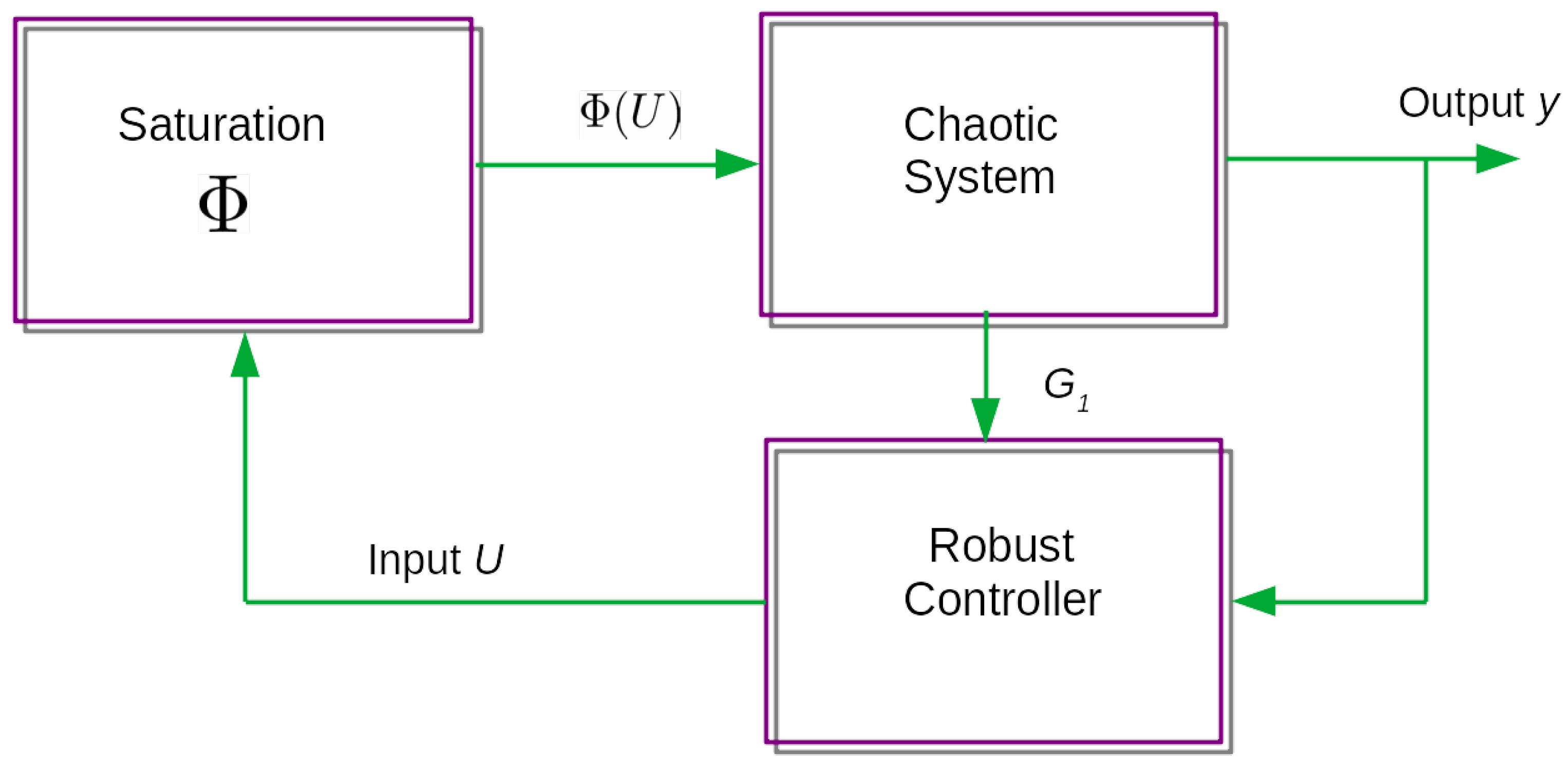
4.1. Robust Stabilization of the Novel Chaotic System
4.2. Robust Synchronization of the Novel Chaotic System
5. Numerical Experiments
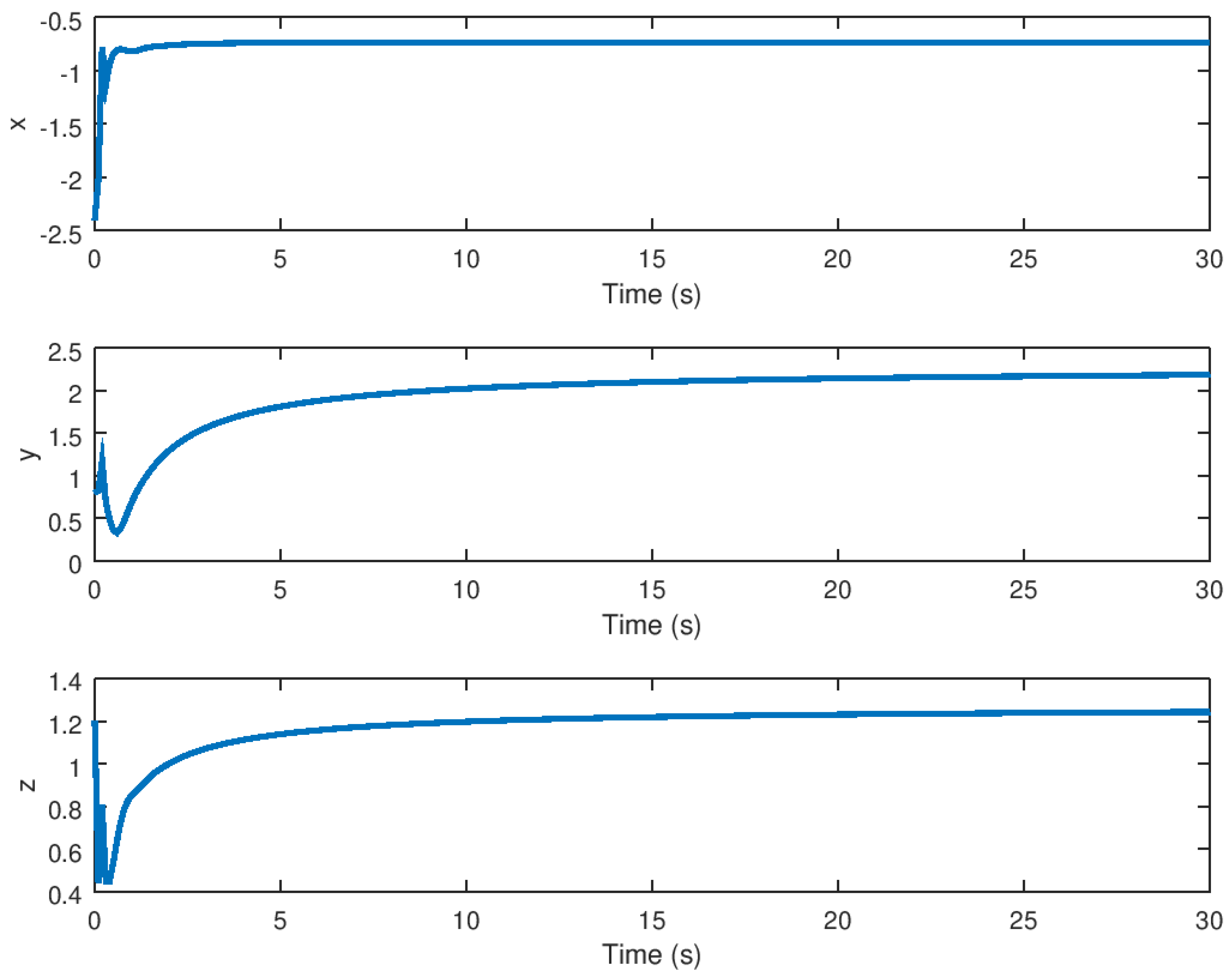
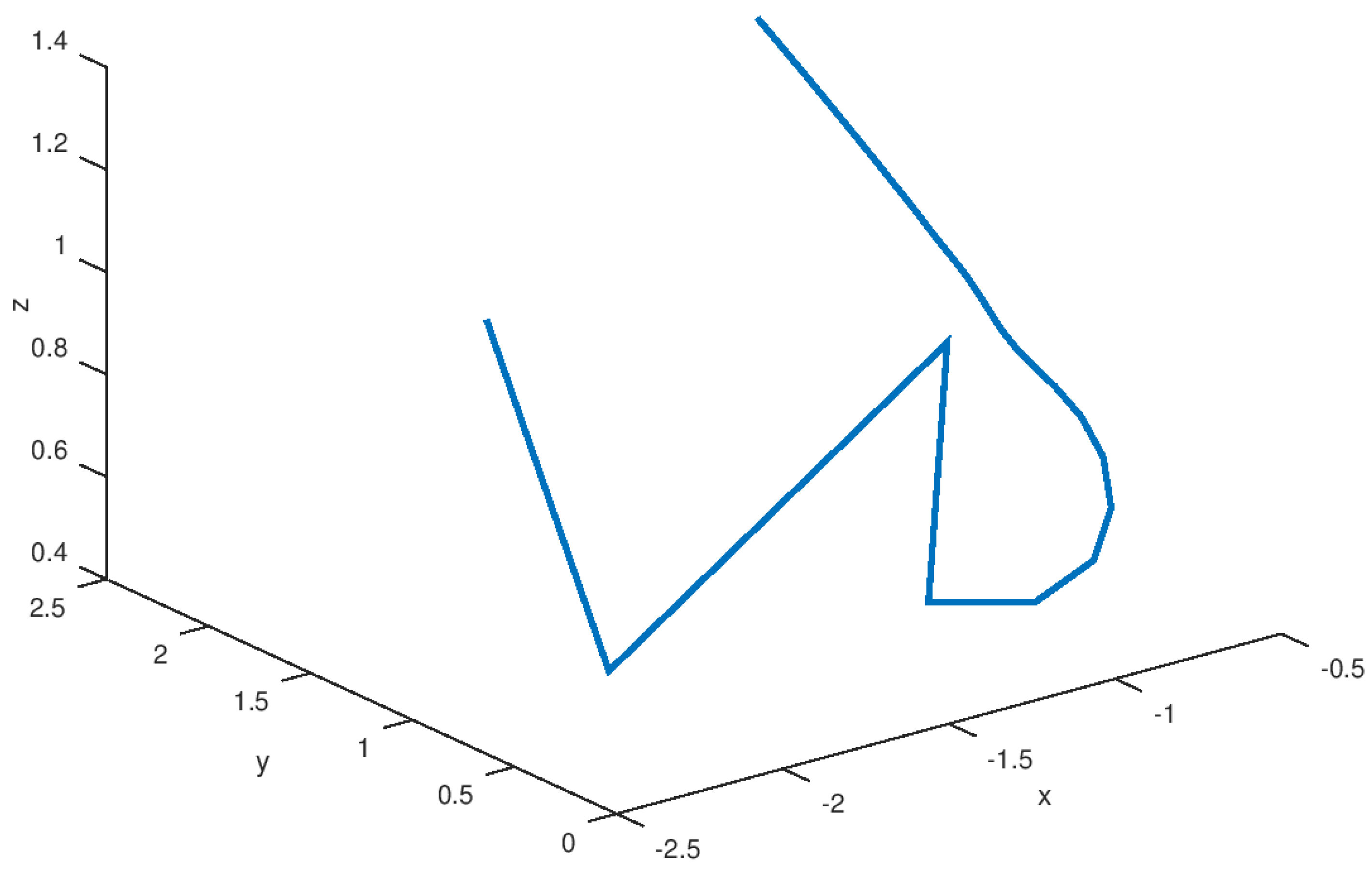
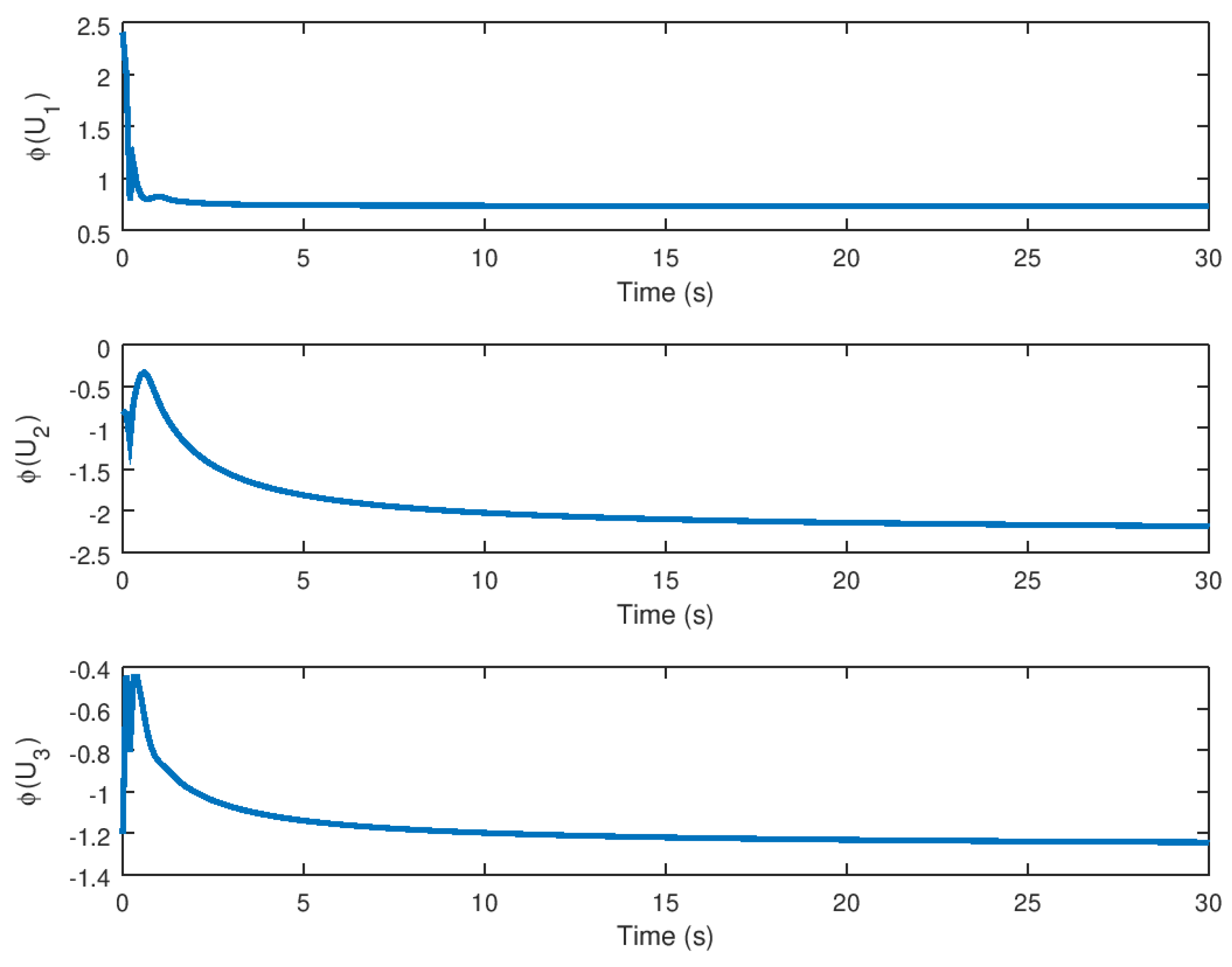
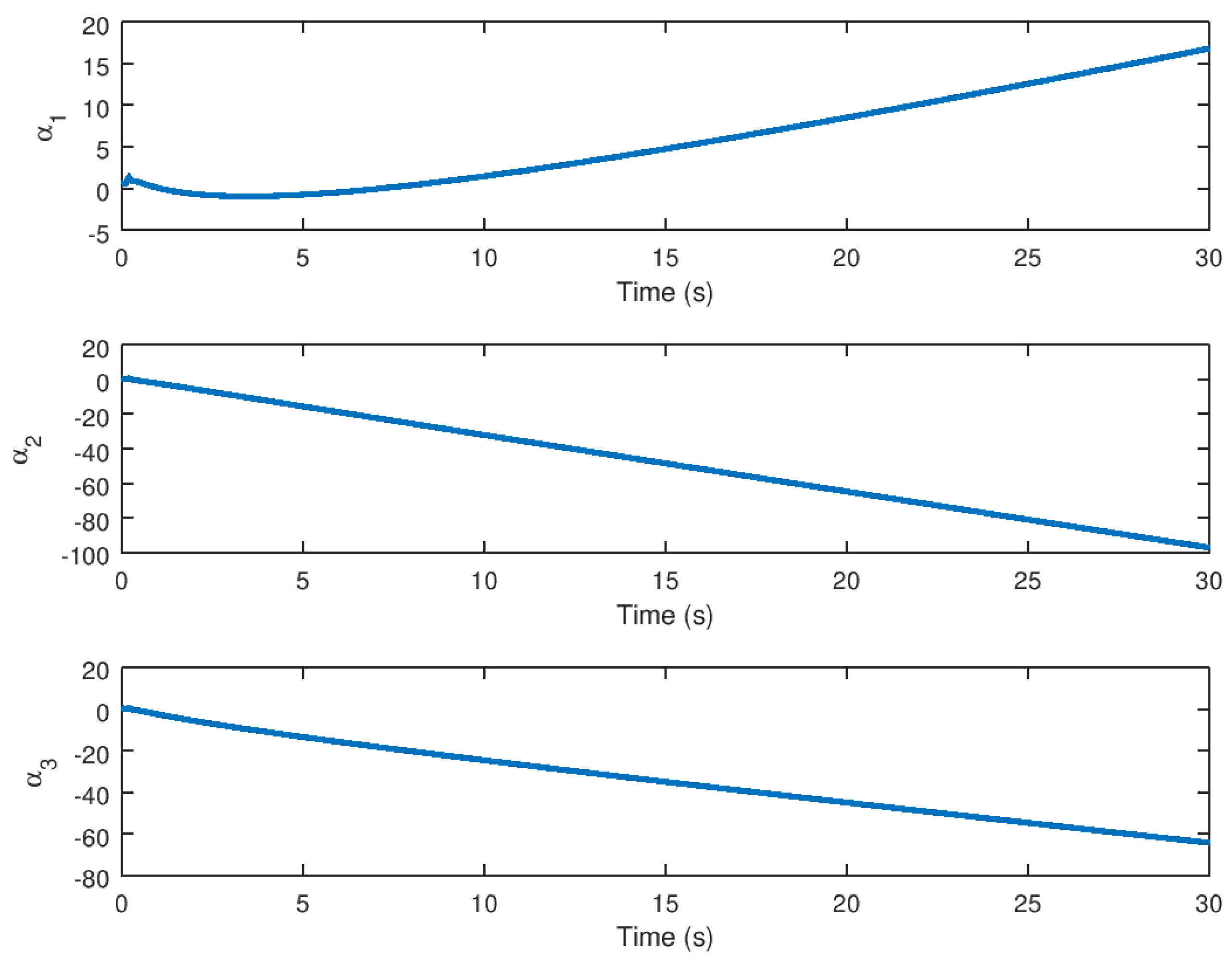
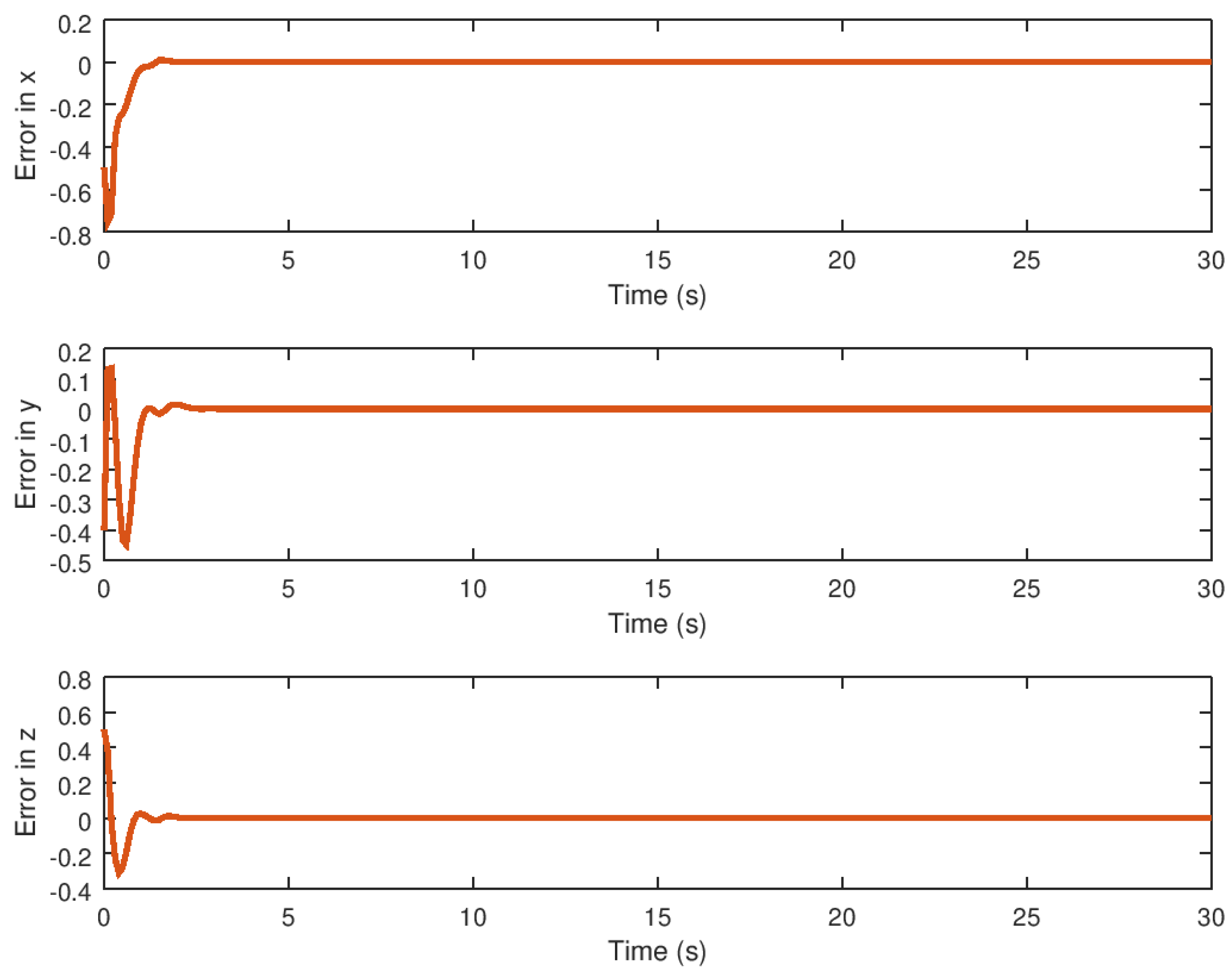
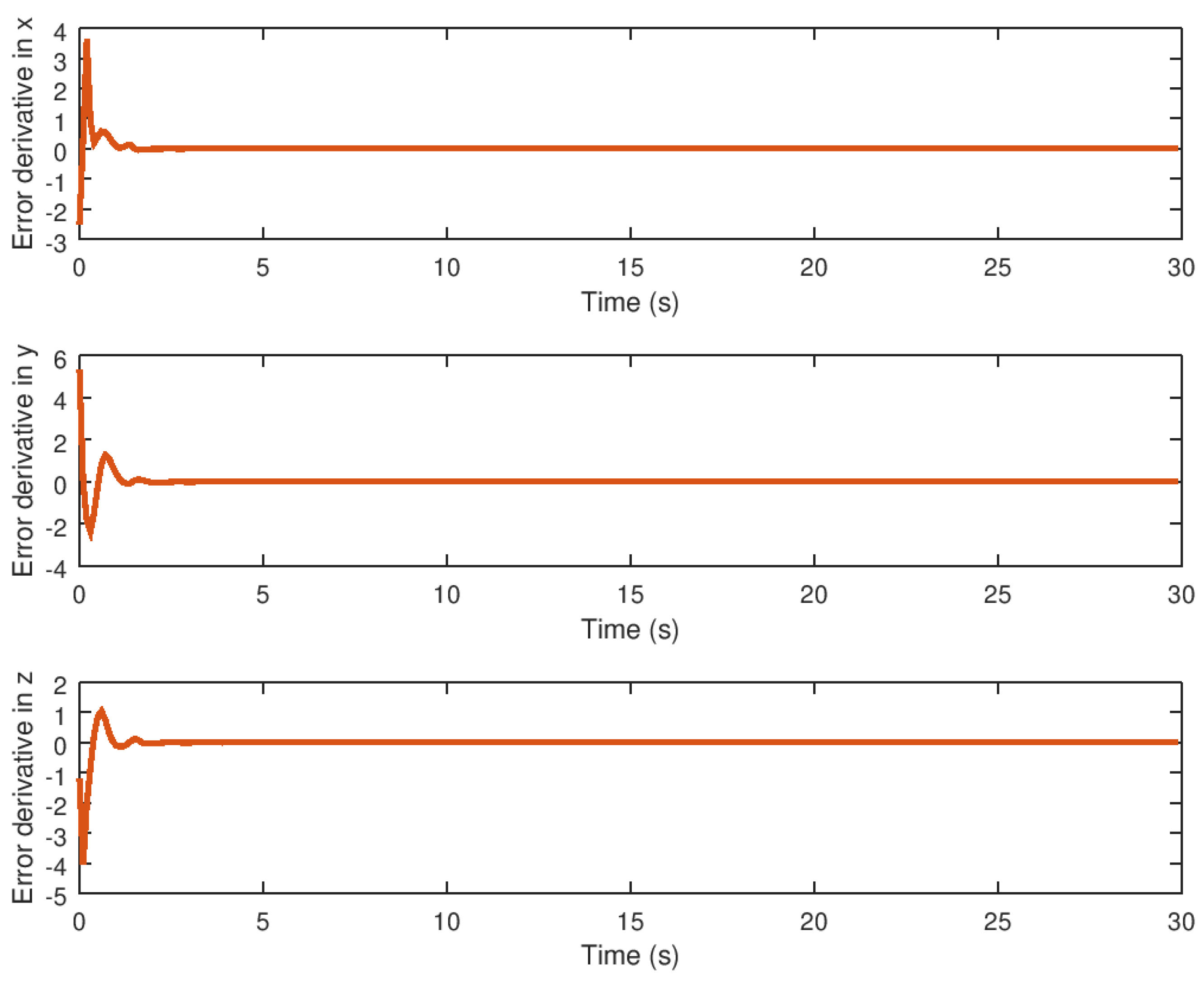
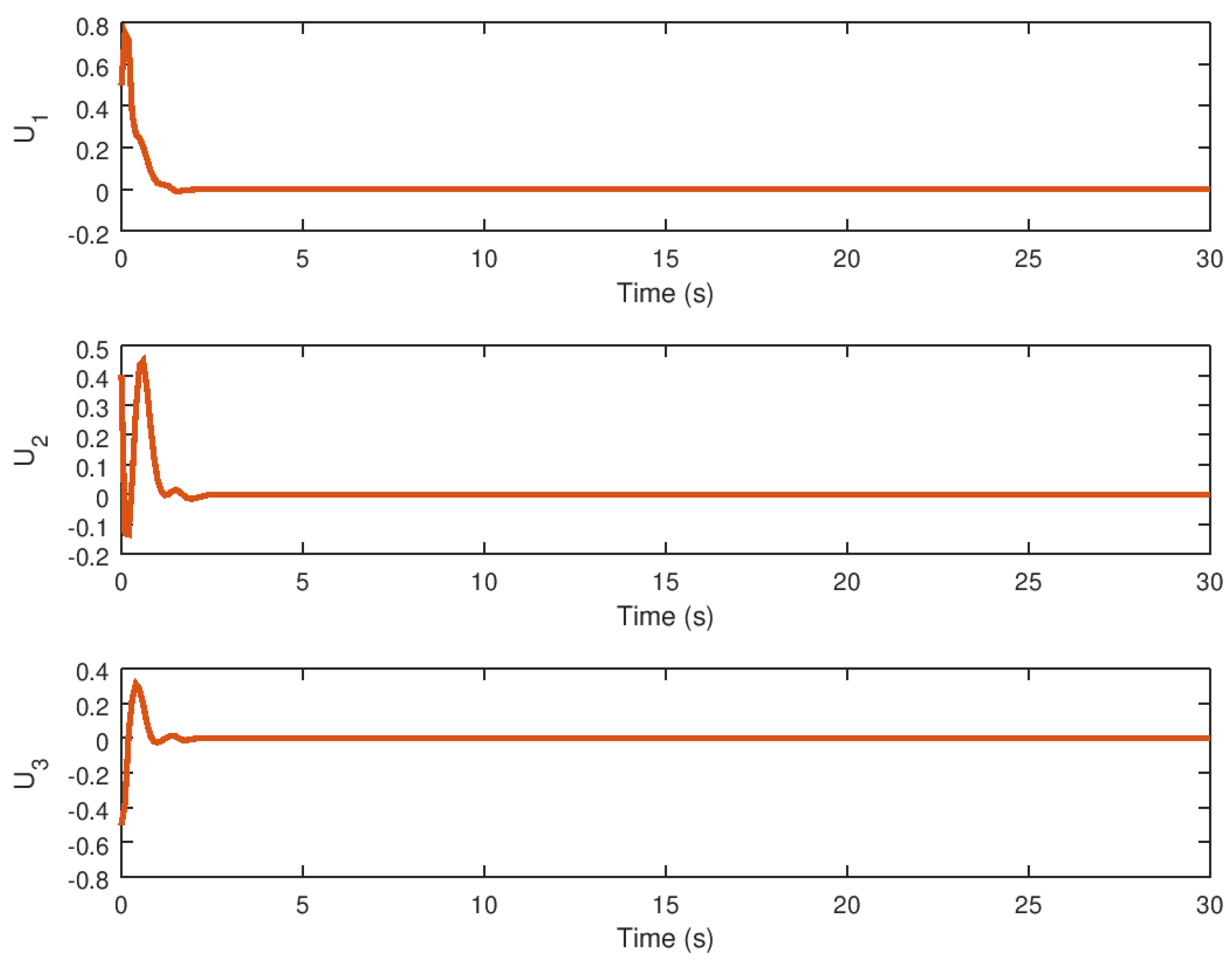
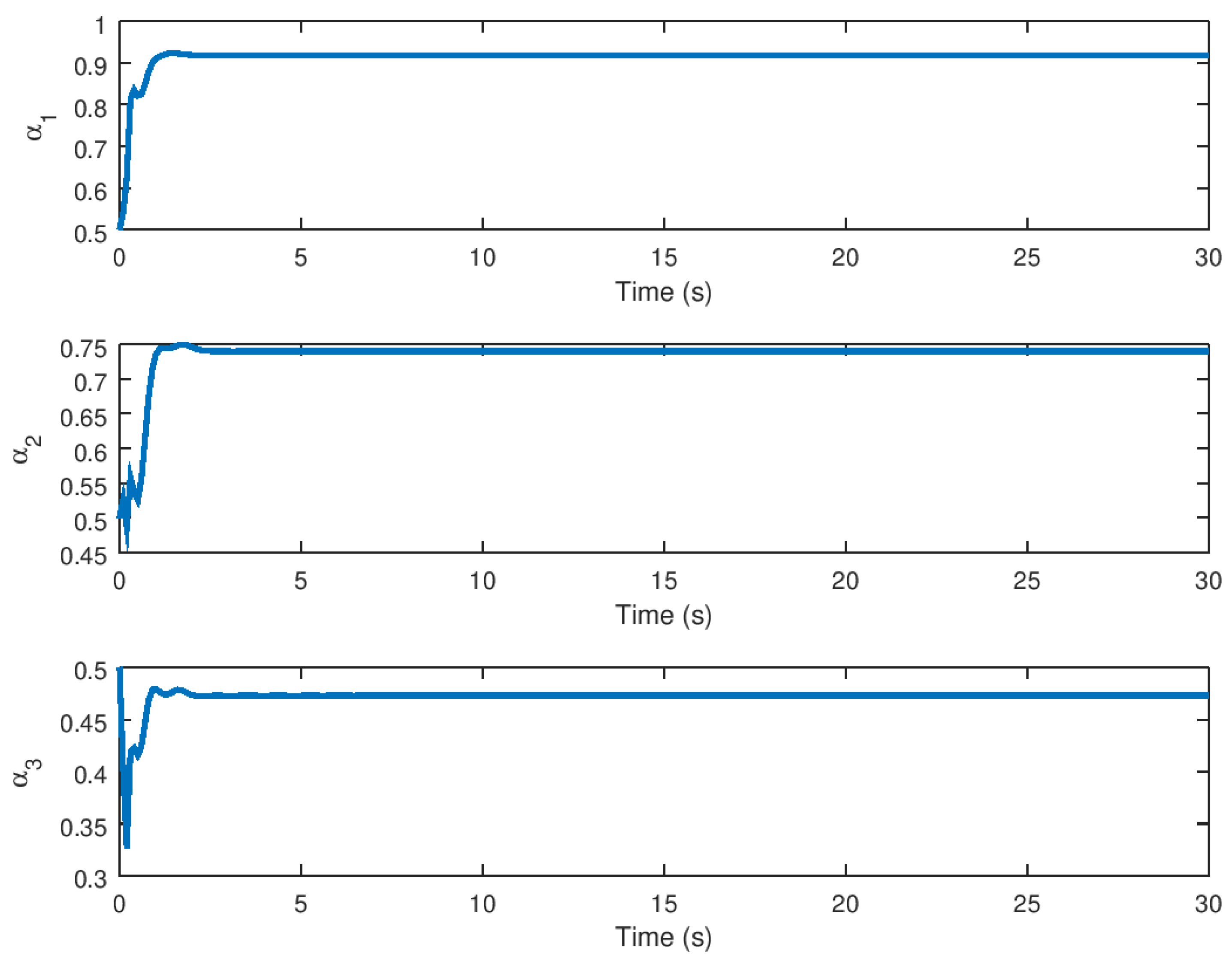
5.1. Experiment 1: Robust Stabilization of the Novel Chaotic System
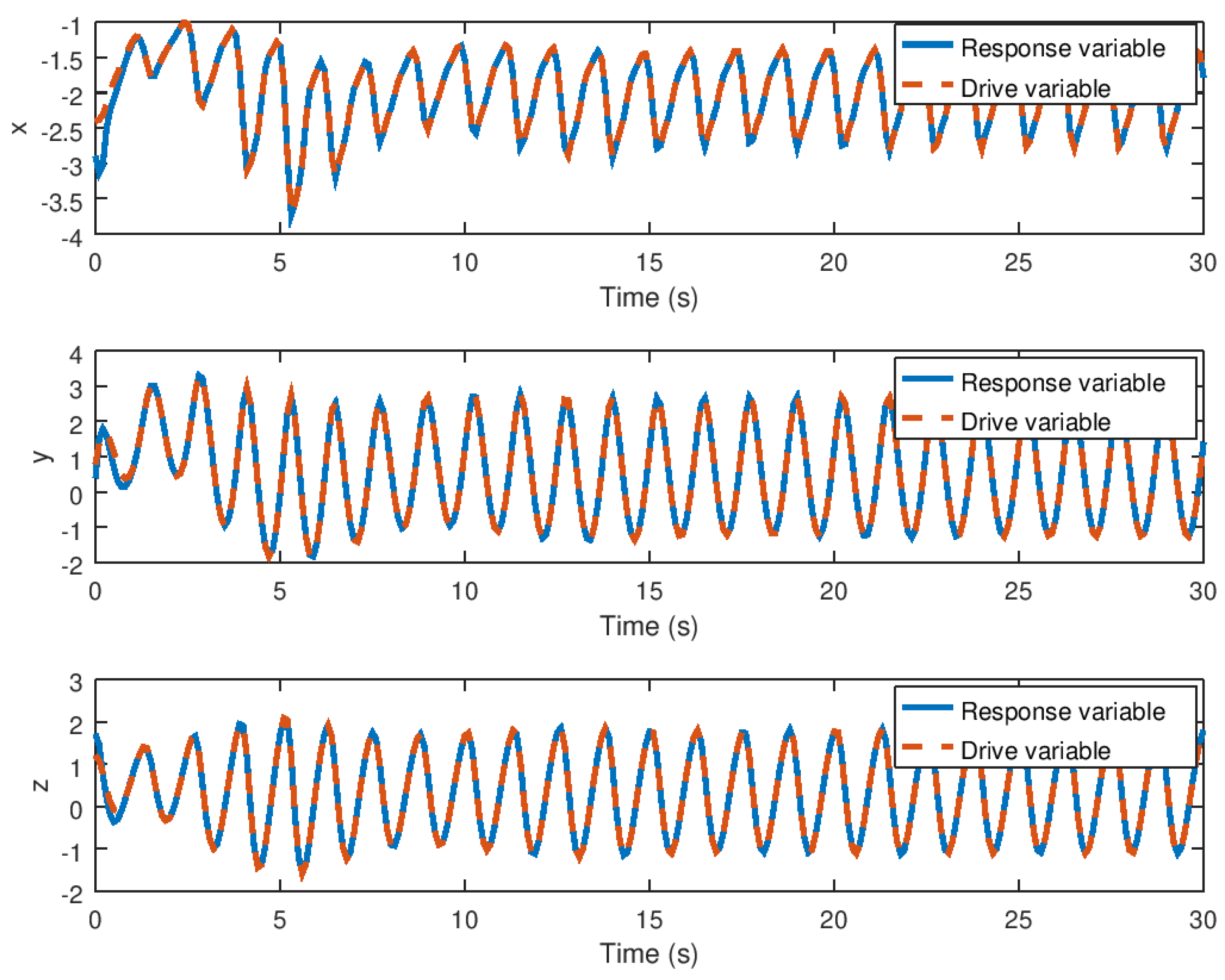
5.2. Experiment 2: Robust Synchronization of the Novel Chaotic System
5.3. Experimental Results Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Danca, M.F.; Lampart, M. Hidden and self-excited attractors in a heterogeneous Cournot oligopoly model. Chaos Solitons Fractals 2021, 142, 110371. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Kuznetsova, O.; Leonov, G.; Mokaev, T.; Stankevich, N. Hidden attractors localization in Chua circuit via the describing function method. IFAC-PapersOnLine 2017, 50, 2651–2656. [Google Scholar] [CrossRef]
- Munmuangsaen, B.; Srisuchinwong, B. A hidden chaotic attractor in the classical Lorenz system. Chaos Solitons Fractals 2018, 107, 61–66. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Ricalde, L.J. Chaos control and synchronization, with input saturation, via recurrent neural networks. Neural Netw. 2003, 16, 711–717. [Google Scholar] [CrossRef]
- Yau, H.T.; Chen, C.L. Chaos control of Lorenz systems using adaptive controller with input saturation. Chaos Solitons Fractals 2007, 34, 1567–1574. [Google Scholar] [CrossRef]
- Zhu, X.; Li, D. Robust attitude control of a 3-DOF helicopter considering actuator saturation. Mech. Syst. Signal Process. 2021, 149, 107209. [Google Scholar] [CrossRef]
- Zhang, J.; Raïssi, T. Saturation control of switched nonlinear systems. Nonlinear Anal. Hybrid Syst. 2019, 32, 320–336. [Google Scholar] [CrossRef]
- Niu, X.; Lin, W.; Gao, X. Static output feedback control of a chain of integrators with input constraints using multiple saturations and delays. Automatica 2021, 125, 109457. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Shi, Y.; Wu, Q. Flexible performance-based robust control for a class of nonlinear systems with input saturation. Automatica 2020, 122, 109268. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.; Kamal, N.A.; Koubaa, A. Robust Kinematic Control of Unmanned Aerial Vehicles with Non-holonomic Constraints. Proc. Int. Conf. Adv. Intell. Syst. Inform. 2020, 1261, 839–850. [Google Scholar]
- Kocamaz, U.E.; Cevher, B.; Uyaroglu, Y. Control and synchronization of chaos with sliding mode control based on cubic reaching rule. Chaos Solitons Fractals 2017, 105, 92–98. [Google Scholar] [CrossRef]
- Aguilar-López, R.; Martínez-Guerra, R. Chaos suppression via observer based active control scheme: Application to Duffing’s oscillator. Chaos Solitons Fractals 2007, 32, 1887–1897. [Google Scholar] [CrossRef]
- Lee, K.W.; Singh, S.N. Robust control of chaos in Chua’s circuit based on internal model principle. Chaos Solitons Fractals 2007, 31, 1095–1107. [Google Scholar] [CrossRef]
- Lin, J.S.; Yan, J.J.; Liao, T.L. Robust control of chaos in Lorenz systems subject to mismatch uncertainties. Chaos Solitons Fractals 2006, 27, 501–510. [Google Scholar] [CrossRef]
- E, J.; Qian, C.; Liu, H.; Liu, G. Design of the H-Infinity robust control for the piezoelectric actuator based on chaos optimization algorithm. Aerosp. Sci. Technol. 2015, 47, 238–246. [Google Scholar] [CrossRef]
- Hu, J.; Qiu, Y.; Lu, H. Adaptive robust nonlinear feedback control of chaos in PMSM system with modeling uncertainty. Appl. Math. Model. 2016, 40, 8265–8275. [Google Scholar] [CrossRef]
- Wei, D.Q.; Luo, X.S.; Wang, B.H.; Fang, J.Q. Robust adaptive dynamic surface control of chaos in permanent magnet synchronous motor. Phys. Lett. A 2007, 363, 71–77. [Google Scholar] [CrossRef]
- Hamiche, H.; Takhi, H.; Messadi, M.; Kemih, K.; Megherbi, O.; Bettayeb, M. New synchronization results for a class of nonlinear discrete-time chaotic systems based on synergetic observer and their implementation. Math. Comput. Simul. 2021, 185, 194–217. [Google Scholar] [CrossRef]
- Hamoudi, A.; Djeghali, N.; Bettayeb, M. Speech encryption based on synchronisation of chaotic Takagi-Sugeno systems using PI observer. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 1285–1290. [Google Scholar] [CrossRef]
- Djennoune, S.; Bettayeb, M.; Saggaf, U.M.A. Impulsive observer with predetermined finite convergence time for synchronization of fractional-order chaotic systems based on Takagi–Sugeno fuzzy model. Nonlinear Dyn. 2019, 98, 331–1354. [Google Scholar] [CrossRef]
- Megherbi, O.; Hamiche, H.; Djennoune, S.; Bettayeb, M. Secure Color Image Transmission Based on the Impulsive Synchronization of Fractional-Order Chaotic Maps Over a Single Channel. In Proceedings of the 4th International Conference on Electrical Engineering and Control Applications; Bououden, S., Chadli, M., Ziani, S., Zelinka, I., Eds.; Springer: Singapore, 2021; pp. 1081–1095. [Google Scholar]
- Djennoune, S.; Bettayeb, M.; Al-Saggaf, U.M. Synchronization of fractional–order discrete–time chaotic systems by an exact delayed state reconstructor: Application to secure communication. Int. J. Appl. Math. Comput. Sci. 2019, 29, 179–194. [Google Scholar] [CrossRef]
- Wang, Z.; Volos, C.; Kingni, S.T.; Azar, A.T.; Pham, V.T. Four-wing attractors in a novel chaotic system with hyperbolic sine nonlinearity. Opt. Int. J. Light Electron Opt. 2017, 131, 1071–1078. [Google Scholar] [CrossRef]
- Bettayeb, M.; Al-Saggaf, U.M.; Djennoune, S. High gain observer design for fractional-order non-linear systems with delayed measurements: Application to synchronisation of fractional-order chaotic systems. IET Control Theory Appl. 2017, 11, 3171–3178. [Google Scholar] [CrossRef]
- Shahverdiev, E.; Bayramov, P.; Qocayeva, M. Inverse chaos synchronization between bidirectionally coupled variable multiple time delay systems. Opt. Int. J. Light Electron Opt. 2013, 124, 3427–3429. [Google Scholar] [CrossRef]
- Mkaouar, H.; Boubaker, O. Chaos synchronization for master slave piecewise linear systems: Application to Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1292–1302. [Google Scholar] [CrossRef]
- Moon, S.; Baik, J.J.; Seo, J.M. Chaos synchronization in generalized Lorenz systems and an application to image encryption. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105708. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T. Dynamic analysis, adaptive feedback control and synchronization of an eight-term 3-D novel chaotic system with three quadratic nonlinearities. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 155–178. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T. A novel 4-D four-wing chaotic system with four quadratic nonlinearities and its synchronization via adaptive control method. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 203–224. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T. Adaptive control and synchronization of Halvorsen circulant chaotic systems. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 225–247. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T. Adaptive backstepping control and synchronization of a novel 3-D jerk system with an exponential nonlinearity. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 249–274. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T. Generalized projective synchronization of a novel hyperchaotic four-wing system via adaptive control method. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 275–290. [Google Scholar]
- Hikihara, T.; Kawagoshi, T. An experimental study on stabilization of unstable periodic motion in magneto-elastic chaos. Phys. Lett. A 1996, 211, 29–36. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.P.; Pham, V.T. On fractional–order discrete–time systems: Chaos, stabilization and synchronization. Chaos Solitons Fractals 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Mukherjee, M.; Halder, S. Stabilization and Control of Chaos Based on Nonlinear Dynamic Inversion. Energy Procedia 2017, 117, 731–738. [Google Scholar] [CrossRef]
- Abed, E.; Wang, H.; Chen, R. Stabilization of period doubling bifurcations and implications for control of chaos. Phys. D Nonlinear Phenom. 1994, 70, 154–164. [Google Scholar] [CrossRef]
- Duan, C.; Yang, S.; Min, W.; Xia, S. Feedback-control to realize and stabilize chaos synchronization. Chaos Solitons Fractals 1998, 9, 921–929. [Google Scholar] [CrossRef]
- Ouannas, A.; Azar, A.T.; Abu-Saris, R. A new type of hybrid synchronization between arbitrary hyperchaotic maps. Int. J. Mach. Learn. Cybern. 2017, 8, 1887–1894. [Google Scholar] [CrossRef]
- Ouannas, A.; Azar, A.T.; Vaidyanathan, S. New hybrid synchronisation schemes based on coexistence of various types of synchronisation between master-slave hyperchaotic systems. Int. J. Comput. Appl. Technol. 2017, 55, 112–120. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T. Qualitative Study and Adaptive Control of a Novel 4-D Hyperchaotic System with Three Quadratic Nonlinearities. In Advances in Chaos Theory and Intelligent Control; Azar, A.T., Vaidyanathan, S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 179–202. [Google Scholar]
- Ouannas, A.; Azar, A.T.; Vaidyanathan, S. A robust method for new fractional hybrid chaos synchronization. Math. Methods Appl. Sci. 2017, 40, 1804–1812. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Anzo-Hernández, A. A novel antimonotic hyperjerk system: Analysis, synchronization and circuit design. Phys. D Nonlinear Phenom. 2021, 424, 132927. [Google Scholar] [CrossRef]
- Shahverdiev, E.; Bayramov, P.; Nuriev, R.; Qocayeva, M.; Hashimova, L. Chaos synchronization between Josephson junctions coupled in series and driven by a central junction. Phys. C Supercond. Its Appl. 2019, 557, 26–32. [Google Scholar] [CrossRef]
- Korneev, I.; Semenov, V.; Slepnev, A.; Vadivasova, T. Complete synchronization of chaos in systems with nonlinear inertial coupling. Chaos Solitons Fractals 2021, 142, 110459. [Google Scholar] [CrossRef]
- Tai, W.; Teng, Q.; Zhou, Y.; Zhou, J.; Wang, Z. Chaos synchronization of stochastic reaction-diffusion time-delay neural networks via non-fragile output-feedback control. Appl. Math. Comput. 2019, 354, 115–127. [Google Scholar] [CrossRef]
- Al Bayati, B.M.; Ahmad, A.K.; Al Naimee, K.A. Effect of control parameters on chaos synchronization by means of optical feedback. Opt. Commun. 2020, 472, 126032. [Google Scholar] [CrossRef]
- Xu, F.; Yu, P. Chaos control and chaos synchronization for multi-scroll chaotic attractors generated using hyperbolic functions. J. Math. Anal. Appl. 2010, 362, 252–274. [Google Scholar] [CrossRef][Green Version]
- Rehan, M. Synchronization and anti-synchronization of chaotic oscillators under input saturation. Appl. Math. Model. 2013, 37, 6829–6837. [Google Scholar] [CrossRef]
- Wang, D.; Zheng, Y. Stabilizing a Class of Chaotic Systems by Using Adaptive Feedback Control. Phys. Procedia 2012, 24, 1922–1927. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Eshmawi, A.A.; Matoog, R. Chaos control and Penta-compound combination anti-synchronization on a novel fractional chaotic system with analysis and application. Results Phys. 2021, 24, 104130. [Google Scholar] [CrossRef]
- Allehiany, F.; Mahmoud, E.E.; Jahanzaib, L.S.; Trikha, P.; Alotaibi, H. Chaos control and analysis of fractional order neural network under electromagnetic radiation. Results Phys. 2021, 21, 103786. [Google Scholar] [CrossRef]
- Tan, T.; Wang, Z.; Zhang, L.; Liao, W.H.; Yan, Z. Piezoelectric autoparametric vibration energy harvesting with chaos control feature. Mech. Syst. Signal Process. 2021, 161, 107989. [Google Scholar] [CrossRef]
- Liu, M.K.; Suh, C.S. Synchronization of chaos in simultaneous time-frequency domain. Appl. Math. Model. 2013, 37, 9524–9537. [Google Scholar] [CrossRef]
- AL-Azzawi, S.F.; Aziz, M.M. Chaos synchronization of nonlinear dynamical systems via a novel analytical approach. Alex. Eng. J. 2018, 57, 3493–3500. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Elsaid, A.; Nour, H. Circuit realization, chaos synchronization and estimation of parameters of a hyperchaotic system with unknown parameters. J. Egypt. Math. Soc. 2014, 22, 550–557. [Google Scholar] [CrossRef]
- El-Sayed, A.; Nour, H.; Elsaid, A.; Matouk, A.; Elsonbaty, A. Dynamical behaviors, circuit realization, chaos control, and synchronization of a new fractional order hyperchaotic system. Appl. Math. Model. 2016, 40, 3516–3534. [Google Scholar] [CrossRef]
- Pusuluri, K.; Meijer, H.; Shilnikov, A. (INVITED) Homoclinic puzzles and chaos in a nonlinear laser model. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105503. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, W. Multiple chaos arising from single-parametric perturbation of a degenerate homoclinic orbit. J. Differ. Equ. 2020, 268, 5672–5703. [Google Scholar] [CrossRef]
- Li, H.; Liao, X.; Huang, J.; Chen, G.; Dong, Z.; Huang, T. Diverting homoclinic chaos in a class of piecewise smooth oscillators to stable periodic orbits using small parametrical perturbations. Neurocomputing 2015, 149, 1587–1595. [Google Scholar] [CrossRef]
- Siewe, M.S.; Hegazy, U.H. Homoclinic bifurcation and chaos control in MEMS resonators. Appl. Math. Model. 2011, 35, 5533–5552. [Google Scholar] [CrossRef]
- Franca, M.; Pospísil, M. New global bifurcation diagrams for piecewise smooth systems: Transversality of homoclinic points does not imply chaos. J. Differ. Equ. 2019, 266, 1429–1461. [Google Scholar] [CrossRef]
- Huaraca, W.; Mendoza, V. Minimal topological chaos coexisting with a finite set of homoclinic and periodic orbits. Phys. D Nonlinear Phenom. 2016, 315, 83–89. [Google Scholar] [CrossRef]
- Li, Z. Chaos induced by heteroclinic cycles connecting repellers and saddles in locally compact metric spaces. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1379–1388. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Y.; Zhang, C. Chaos induced by heteroclinic cycles connecting repellers in complete metric spaces. Chaos Solitons Fractals 2008, 36, 746–761. [Google Scholar] [CrossRef]
- Barajas-Ramírez, J.G.; Franco-López, A.; González-Hernández, H.G. Generating Shilnikov chaos in 3D piecewise linear systems. Appl. Math. Comput. 2021, 395, 125877. [Google Scholar]
- Natiq, H.; Kamel Ariffin, M.R.; Asbullah, M.A.; Mahad, Z.; Najah, M. Enhancing Chaos Complexity of a Plasma Model through Power Input with Desirable Random Features. Entropy 2021, 23, 48. [Google Scholar] [CrossRef]
- Sándor, B.; Schneider, B.; Lázár, Z.I.; Ercsey-Ravasz, M. A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks. Entropy 2021, 23, 103. [Google Scholar] [CrossRef]
- Petrzela, J. Evidence of Strange Attractors in Class C Amplifier with Single Bipolar Transistor: Polynomial and Piecewise-Linear Case. Entropy 2021, 23, 175. [Google Scholar] [CrossRef]
- Ribeiro, M.; Henriques, T.; Castro, L.; Souto, A.; Antunes, L.; Costa-Santos, C.; Teixeira, A. The Entropy Universe. Entropy 2021, 23, 222. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, T.; Zhao, T.; Zhang, H.; Guo, X. Chaotic Time-Delay Signature Suppression and Entropy Growth Enhancement Using Frequency-Band Extractor. Entropy 2021, 23, 516. [Google Scholar] [CrossRef]
- Marszalek, W.; Sadecki, J.; Walczak, M. Computational Analysis of Ca2+ Oscillatory Bio-Signals: Two-Parameter Bifurcation Diagrams. Entropy 2021, 23, 876. [Google Scholar] [CrossRef] [PubMed]
- Dénes, K.; Sándor, B.; Néda, Z. Synchronization patterns in rings of time-delayed Kuramoto oscillators. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105505. [Google Scholar] [CrossRef]
- Shang, D.; Shang, P.; Zhang, Z. Efficient synchronization estimation for complex time series using refined cross-sample entropy measure. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105556. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Kecik, K. Simultaneous vibration mitigation and energy harvesting from a pendulum-type absorber. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105479. [Google Scholar] [CrossRef]
- Montes, J.; Revuelta, F.; Borondo, F. Lagrangian descriptors and regular motion. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105860. [Google Scholar] [CrossRef]
- Salas, J.P.; Iñarrea, M.; Lanchares, V.; Palacián, J.; Yanguas, P. Magnetic confinement of a neutral atom in a double-wire waveguide: A nonlinear dynamics approach. Commun. Nonlinear Sci. Numer. Simul. 2021, 101, 105662. [Google Scholar] [CrossRef]
- Adewole, A.; Falayi, E.; Roy-Layinde, T.; Adelaja, A. Chaotic time series analysis of meteorological parameters in some selected stations in Nigeria. Sci. Afr. 2020, 10, e00617. [Google Scholar] [CrossRef]
- Chabab, M.; El Moumni, H.; Iraoui, S.; Masmar, K.; Zhizeh, S. Chaos in charged AdS black hole extended phase space. Phys. Lett. B 2018, 781, 316–321. [Google Scholar] [CrossRef]
- Shirmohammadi, F.; Tohidi, A. Mixing enhancement using chaos theory in fluid dynamics: Experimental and numerical study. Chem. Eng. Res. Des. 2019, 141, 350–360. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control. Entropy 2020, 22, 122. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azar, A.T.; Serrano, F.E.; Zhu, Q.; Bettayeb, M.; Fusco, G.; Na, J.; Zhang, W.; Kamal, N.A. Robust Stabilization and Synchronization of a Novel Chaotic System with Input Saturation Constraints. Entropy 2021, 23, 1110. https://doi.org/10.3390/e23091110
Azar AT, Serrano FE, Zhu Q, Bettayeb M, Fusco G, Na J, Zhang W, Kamal NA. Robust Stabilization and Synchronization of a Novel Chaotic System with Input Saturation Constraints. Entropy. 2021; 23(9):1110. https://doi.org/10.3390/e23091110
Chicago/Turabian StyleAzar, Ahmad Taher, Fernando E. Serrano, Quanmin Zhu, Maamar Bettayeb, Giuseppe Fusco, Jing Na, Weicun Zhang, and Nashwa Ahmad Kamal. 2021. "Robust Stabilization and Synchronization of a Novel Chaotic System with Input Saturation Constraints" Entropy 23, no. 9: 1110. https://doi.org/10.3390/e23091110
APA StyleAzar, A. T., Serrano, F. E., Zhu, Q., Bettayeb, M., Fusco, G., Na, J., Zhang, W., & Kamal, N. A. (2021). Robust Stabilization and Synchronization of a Novel Chaotic System with Input Saturation Constraints. Entropy, 23(9), 1110. https://doi.org/10.3390/e23091110









