Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector
Abstract
1. Introduction
2. Preliminaries
2.1. Basic Notations
2.2. FO Calculus
- The Marchaud derivative of the order of the function f exists, if and as for some (see Section 5.4 in [31]). If additionally for , then the Marchaud derivative coincides with the Riemann-Liouville derivative with a base point .
- For the derivative of the order of the exponent (where is fixed), one obtainsfor . As discussed in [34] (see (5) therein), this limitation stems from the memory of derivative, which covers the entire interval . Therefore, allowing for would lead to divergent integrals. In practical terms, it is not a limitation, because one should consider functions bounded at , or even causal (i.e., equal to zero for arguments in .
- When the Marchaud derivative coincides with the Grünwald-Letnikov derivative for the function f, then one obtainswhere .
- In some cases, we would like to assume not only that the Marchaud derivative of the function exists, but also that this derivative belongs to an appropriate space . It is handled by Theorems 6.1 and 6.5 in [31]. The condition that guarantees that is that and for . The function space denotes the space of Hölder continuous functions with appropriate behaviour in (see (1.5) and (1.6) in [31]). One can check that, in order to belong to , it is enough to assume that andfor . The last condition is satisfied, e.g., when as .
- We employ in our considerations some properties of the null space of the Marchaud derivative. We are not aware of any general result in this area, but we can show some reasonable behaviour assuming that is a Hölder continuous function. That is, if one assumes that with exponent and , then implies . This is a consequence of Theorems 6.1 and 6.5 from [31].
- The appropriate Fourier transformation identity can be formulated for the Marchaud derivative (see formula (7.4) in [31])when , , and f along with derivatives up to the order n belongs to .
2.3. Vector Fields
3. RS Vector
4. Plane-Wave Propagation
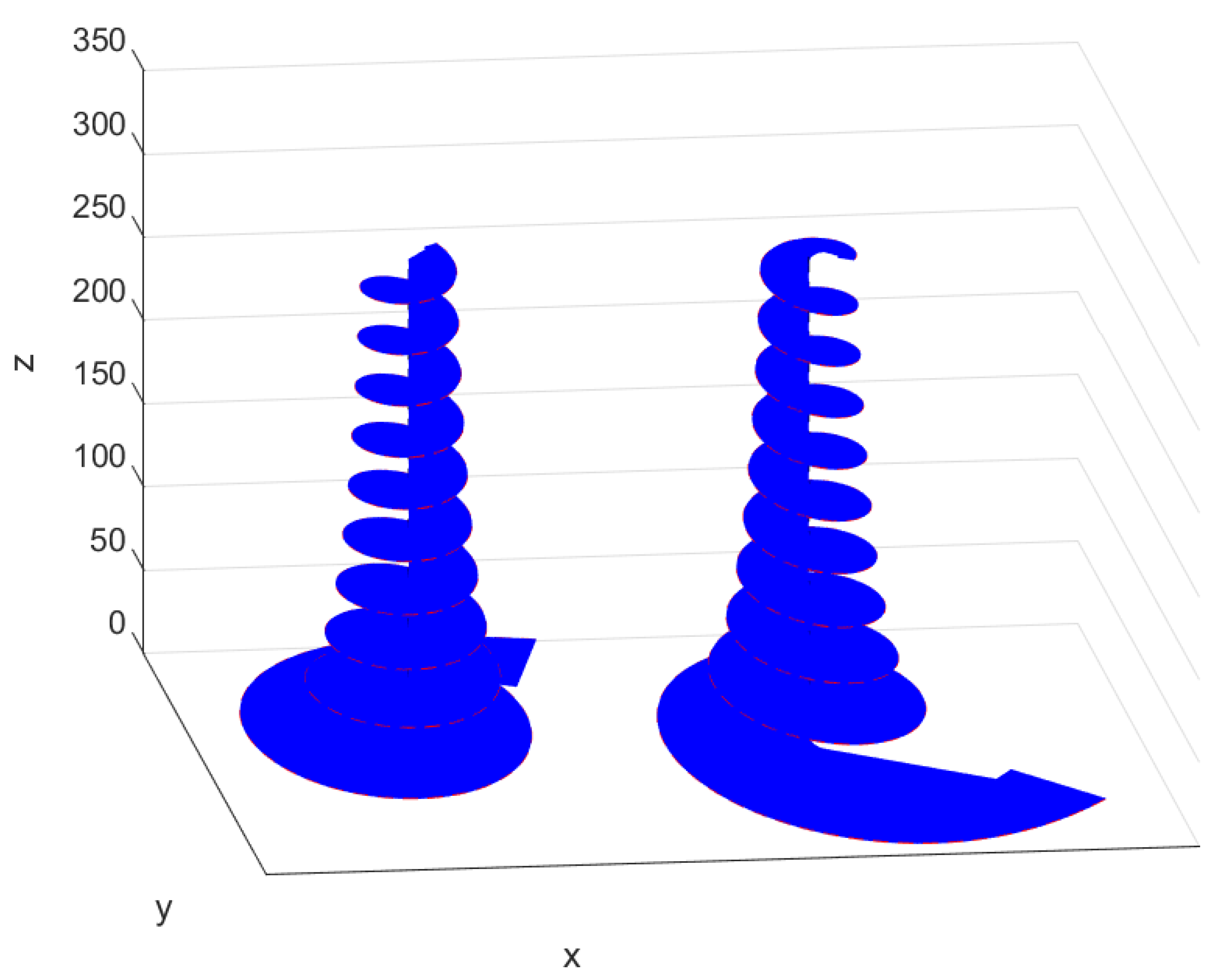
5. Fundamental Solutions
6. Power Conservation
7. Momentum Conservation
8. Uniqueness of Solutions
9. Reciprocity
10. Causality
- (i)
- The inverse Fourier transform of vanishes for :
- (ii)
- is, for almost all v, the limit as of an analytic function that is holomorphic in the right half-plane and square integrable over any line parallel to the imaginary axis:
- (iii)
- and verify the first Plemelj formula:
- (iv)
- and verify the second Plemelj formula:
- (i)
- for each function F restricted to the set is of order/type
- (ii)
- is finite
- (iii)
- there exists such that for all the function satisfies .
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baleanu, D.; Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, M.C. Fractional Electromagnetic Equations Using Fractional Forms. Int. J. Theor. Phys. 2009, 48, 3114–3123. [Google Scholar] [CrossRef]
- Lazo, M.J. Gauge invariant fractional electromagnetic fields. Phys. Lett. A 2011, 375, 3541–3546. [Google Scholar] [CrossRef]
- Jaradat, E.K.; Hijjawi, R.S.; Khalifeh, J.M. Maxwell’s equations and electromagnetic Lagrangian density in fractional form. J. Math. Phys. 2012, 53, 033505. [Google Scholar] [CrossRef]
- Rabei, E.M.; Al-Jamel, A.; Widyan, H.; Baleanu, D. Comment on “Maxwell’s equations and electromagnetic Lagrangian density in fractional form” [J. Math. Phys. 53, 033505 (2012)]. J. Math. Phys. 2014, 55, 034101. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar] [CrossRef]
- Engheta, N. Fractional curl operator in electromagnetics. Microw. Opt. Technol. Lett. 1998, 17, 86–91. [Google Scholar] [CrossRef]
- Naqvi, Q.; Abbas, M. Complex and higher order fractional curl operator in electromagnetics. Opt. Commun. 2004, 241, 349–355. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Bogolyubov, A.N.; Potapov, A.A.; Rehviashvili, S.S. An approach to introducing fractional integro-differentiation in classical electrodynamics. Mosc. Univ. Phys. Bull. 2009, 64, 365–368. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor. Math. Phys. 2009, 158, 355–359. [Google Scholar] [CrossRef]
- Tarasov, V. Fractional Dynamics: Application of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nasrolahpour, H. A note on fractional electrodynamics. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2589–2593. [Google Scholar] [CrossRef]
- Westerlund, S. Dead matter has memory! Phys. Scr. 1991, 43, 174–179. [Google Scholar] [CrossRef]
- Engheta, N. On fractional calculus and fractional multipoles in electromagnetism. IEEE Trans. Antennas Propag. 1996, 44, 554–566. [Google Scholar] [CrossRef]
- Engheta, N. On the role of fractional calculus in electromagnetic theory. IEEE Antennas Propag. Mag. 1997, 39, 35–46. [Google Scholar] [CrossRef]
- Machado, J.T.; Jesus, I.S.; Galhano, A.; Cunha, J.B. Fractional order electromagnetics. Signal Process. 2006, 86, 2637–2644. [Google Scholar] [CrossRef]
- Veliev, E.I.; Engheta, N. Fractional curl operator in reflection problems. In Proceedings of the 10th International Conference on Mathematical Methods in Electromagnetic Theory, Dniepropetrovsk, Ukraine, 14–17 September 2004; pp. 228–230. [Google Scholar] [CrossRef]
- Ivakhnychenko, M.V.; Veliev, E.I.; Ahmedov, T.M. Fractional Operators Approach in Electromagnetic Wave Reflection Problems. J. Electromagn. Waves Appl. 2007, 21, 1787–1802. [Google Scholar] [CrossRef]
- Veliev, E.I.; Ivakhnychenko, M.V.; Ahmedov, T.M. Fractional boundary conditions in plane waves diffraction on a strip. Prog. Electromagn. Res. 2008, 79, 443–462. [Google Scholar] [CrossRef][Green Version]
- Naqvi, S.; Naqvi, Q.; Hussain, A. Modelling of transmission through a chiral slab using fractional curl operator. Opt. Commun. 2006, 266, 404–406. [Google Scholar] [CrossRef]
- Weber, H. Die Partiellen Differential-Gleichungen Der Mathematischen Physik: Nach Riemann’s Vorlesungen Bearbeitet von Heinrich Weber; Friedrich Vieweg und Sohn: Braunschweig, Germany, 1901. [Google Scholar]
- Silberstein, L. Elektromagnetische Grundgleichungen in bivektorieller Behandlung. Ann. Phys. 1907, 327, 579–586. [Google Scholar] [CrossRef]
- Silberstein, L. Nachtrag zur Abhandlung uber “Elektromagnetische Grundgleichungen in bivektorieller Behandlung”. Ann. Phys. 1907, 329, 783–784. [Google Scholar] [CrossRef]
- Silberstein, L. LXXVI. Quaternionic form of relativity. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1912, 23, 790–809. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. The role of the Riemann–Silberstein vector in classical and quantum theories of electromagnetism. J. Phys. Math. Theor. 2013, 46, 053001. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. V Photon Wave Function. Prog. Opt. 1996, 36, 245–294. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Exponential Localization of Photons. Phys. Rev. Lett. 1998, 80, 5247–5250. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. Beams of electromagnetic radiation carrying angular momentum: The Riemann-Silberstein vector and the classical-quantum correspondence. Opt. Commun. 2006, 264, 342–351. [Google Scholar] [CrossRef]
- Belkovich, I.V.; Kogan, B.L. Utilization of Riemann-Silberstein Vectors in Electromagnetics. Prog. Electromagn. Res. B 2016, 69, 103–116. [Google Scholar] [CrossRef][Green Version]
- Belkovich, I.V.; Kogan, B.L. The Riemann-Silberstein vectors theory and vector spherical expansion. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Spring (PIERS), Singapore, 19–22 November 2017; pp. 2346–2355. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Gulgowski, J.; Stefanski, T.P. On Applications of Fractional Derivatives in Electromagnetic Theory. In Proceedings of the 2020 23rd International Conference on Microwave, Radar and Wireless Communications (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 1–4. [Google Scholar]
- Gulgowski, J.; Stefański, T.P.; Trofimowicz, D. On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory. Energies 2020, 13, 5768. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Signal propagation in electromagnetic media described by fractional-order models. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105029. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Moreles, M.A.; Lainez, R. Mathematical modelling of fractional order circuit elements and bioimpedance applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 46, 81–88. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Curie, M.J. Recherches sur La Conductibilit Des Corps Cristallises. Ann. Chim. Phys. 1889, 18, 203–269. [Google Scholar]
- Naber, M. Time fractional Schrödinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar] [CrossRef]
- Achar, B.N.N.; Yale, B.T.; Hanneken, J.W. Time Fractional Schrödinger Equation Revisited. Adv. Math. Phys. 2013, 2013, 290216. [Google Scholar] [CrossRef]
- Iomin, A. Fractional evolution in quantum mechanics. Chaos Solitons Fractals 2019, 1, 100001. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135–3145. [Google Scholar] [CrossRef]
- Ryabov, Y.E.; Puzenko, A. Damped oscillations in view of the fractional oscillator equation. Phys. Rev. B 2002, 66, 184201. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F.; Povstenko, Y. Propagation speed of the maximum of the fundamental solution to the fractional diffusion–wave equation. Comput. Math. Appl. 2013, 66, 774–784. [Google Scholar] [CrossRef]
- Luchko, Y. Fractional wave equation and damped waves. J. Math. Phys. 2013, 54, 031505. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F. Cauchy and Signaling Problems for the Time-Fractional Diffusion-Wave Equation. J. Vib. Acoust. 2014, 136, 051008/1–051008/7. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Re-published by Cambridge University Press in 2017; Pearson: Boston, MA, USA, 2013. [Google Scholar]
- Balazs, N.L. The Energy-Momentum Tensor of the Electromagnetic Field inside Matter. Phys. Rev. 1953, 91, 408–411. [Google Scholar] [CrossRef]
- Griffiths, D.J. Resource Letter EM-1: Electromagnetic Momentum. Am. J. Phys. 2012, 80, 7–18. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F. Some properties of the fundamental solution to the signalling problem for the fractional diffusion-wave equation. Cent. Eur. J. Phys. 2013, 11, 666–675. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Fundamental properties of solutions to fractional-order Maxwell’s equations. J. Electromagn. Waves Appl. 2020, 34, 1955–1976. [Google Scholar] [CrossRef]
- Gulgowski, J.; Stefański, T.P. Generalization of Kramers-Krönig relations for evaluation of causality in power-law media. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105664. [Google Scholar] [CrossRef]
- Gibson, W. The Method of Moments in Electromagnetics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Stefanski, T.P.; Gulgowski, J. Simulation of Wave Propagation in Media Described by Fractional-Order Models. In Proceedings of the 2020 23rd International Microwave and Radar Conference (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 34–39. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Electromagnetic-based derivation of fractional-order circuit theory. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104897. [Google Scholar] [CrossRef]
- Davidovich, M.V. On energy and momentum conservation laws for an electromagnetic field in a medium or at diffraction on a conducting plate. Phys.-Uspekhi 2010, 53, 595–609. [Google Scholar] [CrossRef]
- Campos, I.; Jimenez, J.; Lopez-Marino, M. Electromagnetic momentum balance equation and the force density in material media. Rev. Bras. Ensino Sica 2012, 34, 1–5. [Google Scholar] [CrossRef]
- Campos, I.; Jiménez, J.L.; Roa-Neri, J.A.E. Radiation force and balance of electromagnetic momentum. Eur. J. Phys. 2016, 37, 045201. [Google Scholar] [CrossRef]
- Campos, I.; Jiménez, J.L.; Roa-Neri, J.A.E. Balance Equations of Electromagnetic Angular Momentum. J. Electromagn. Anal. Appl. 2017, 9, 203–217. [Google Scholar] [CrossRef]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; IEEE-Press: Piscataway Township, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Nussenzveig, H. Causality and Dispersion Relations; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Abramowitz, M. Handbook of Mathematical Functions, With Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: Mineola, NY, USA, 1974. [Google Scholar]
- Carlsson, M.; Wittsten, J. A note on holomorphic functions and the Fourier-Laplace transform. Math. Scand. 2017, 120, 225–248. [Google Scholar] [CrossRef]


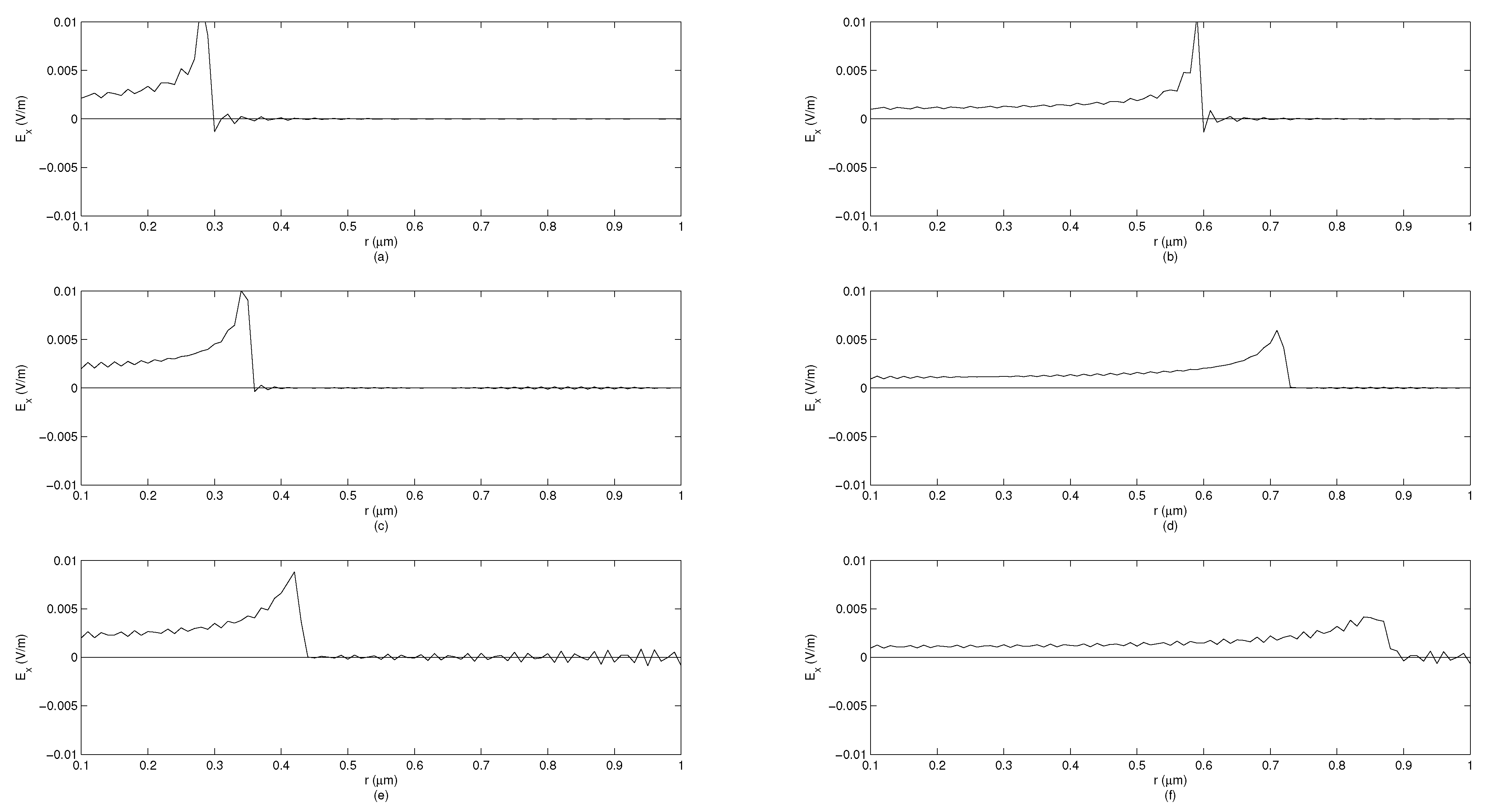

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefański, T.P.; Gulgowski, J. Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector. Entropy 2021, 23, 987. https://doi.org/10.3390/e23080987
Stefański TP, Gulgowski J. Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector. Entropy. 2021; 23(8):987. https://doi.org/10.3390/e23080987
Chicago/Turabian StyleStefański, Tomasz P., and Jacek Gulgowski. 2021. "Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector" Entropy 23, no. 8: 987. https://doi.org/10.3390/e23080987
APA StyleStefański, T. P., & Gulgowski, J. (2021). Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector. Entropy, 23(8), 987. https://doi.org/10.3390/e23080987





