Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach
Abstract
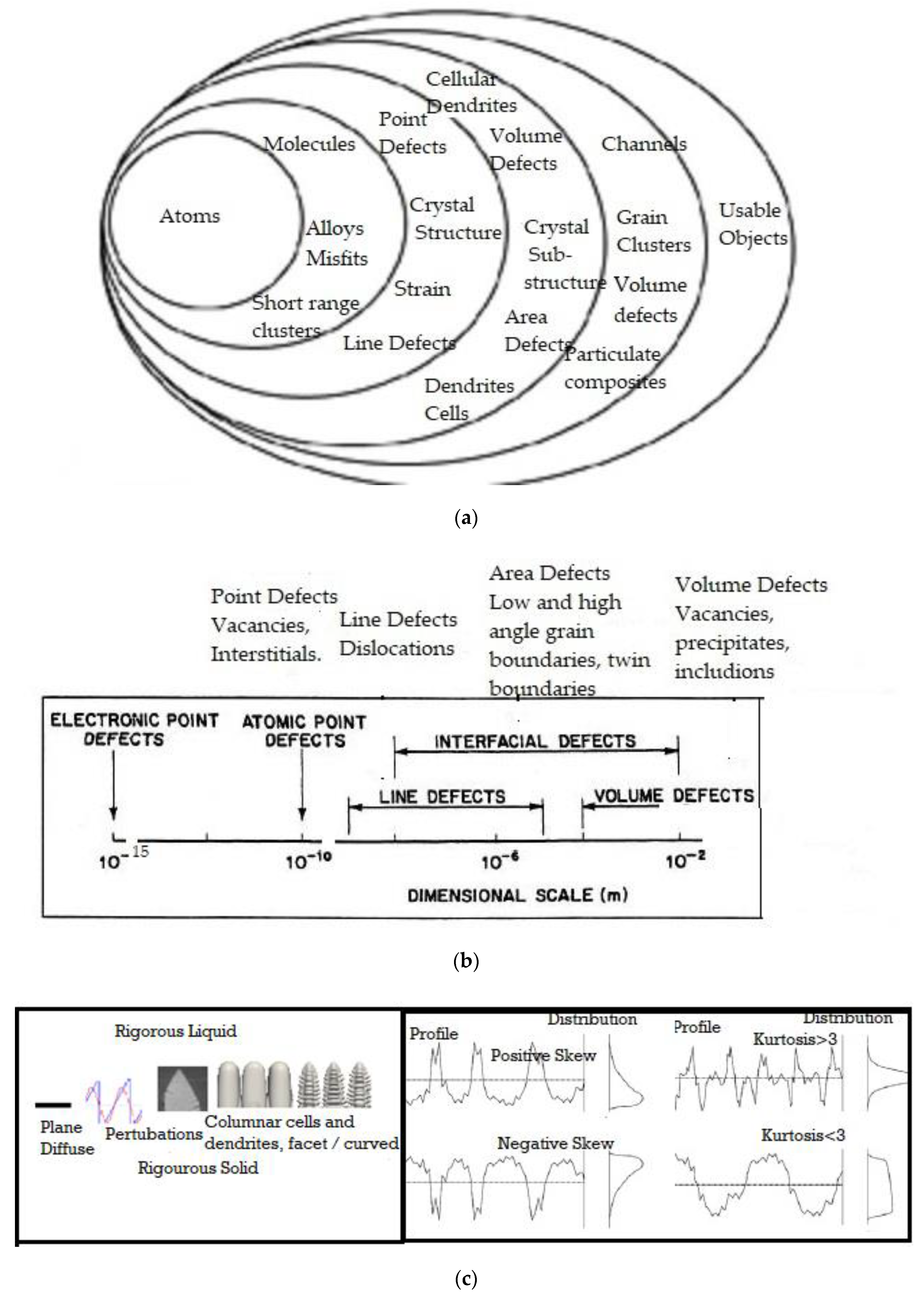
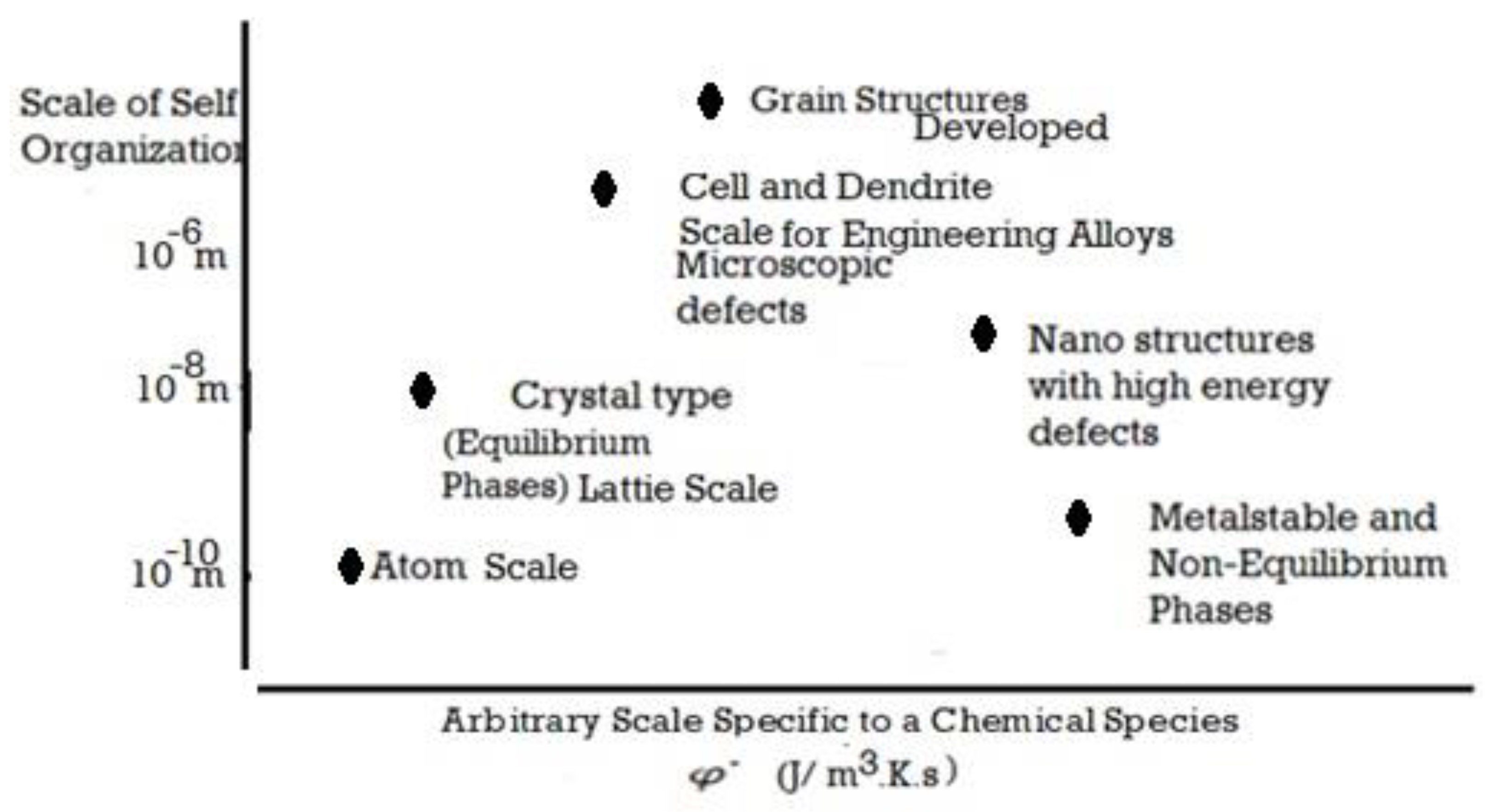
1. Introduction
2. Formalism
Steady State
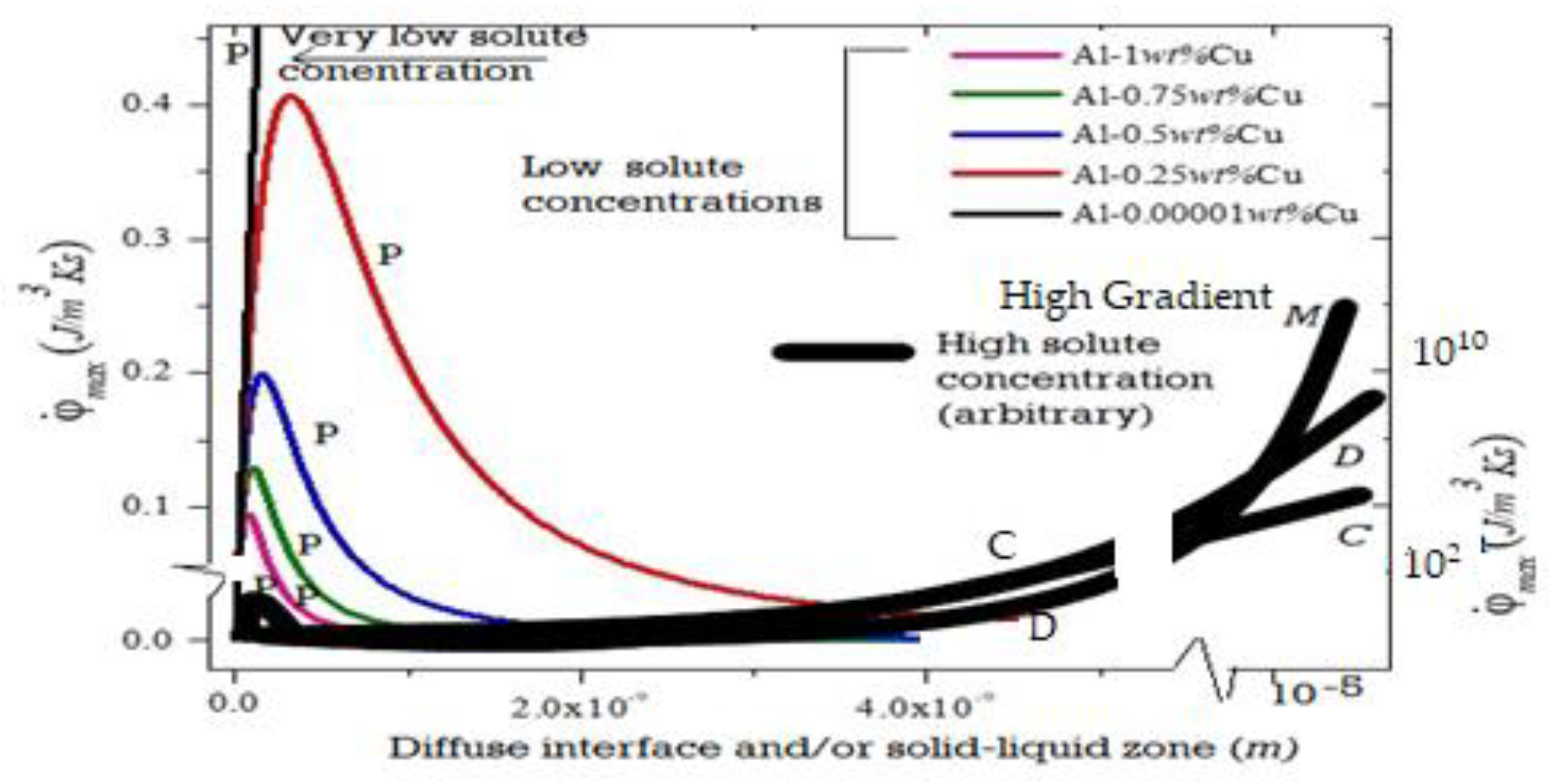
3. Maximum Entropy Production Rate (MEPR) Principle
4. Patterns and Texture Examples from Directional Solidification, Wear, and Friction
4.1. Low-Velocity Transitions, Facets to Smooth Curvature
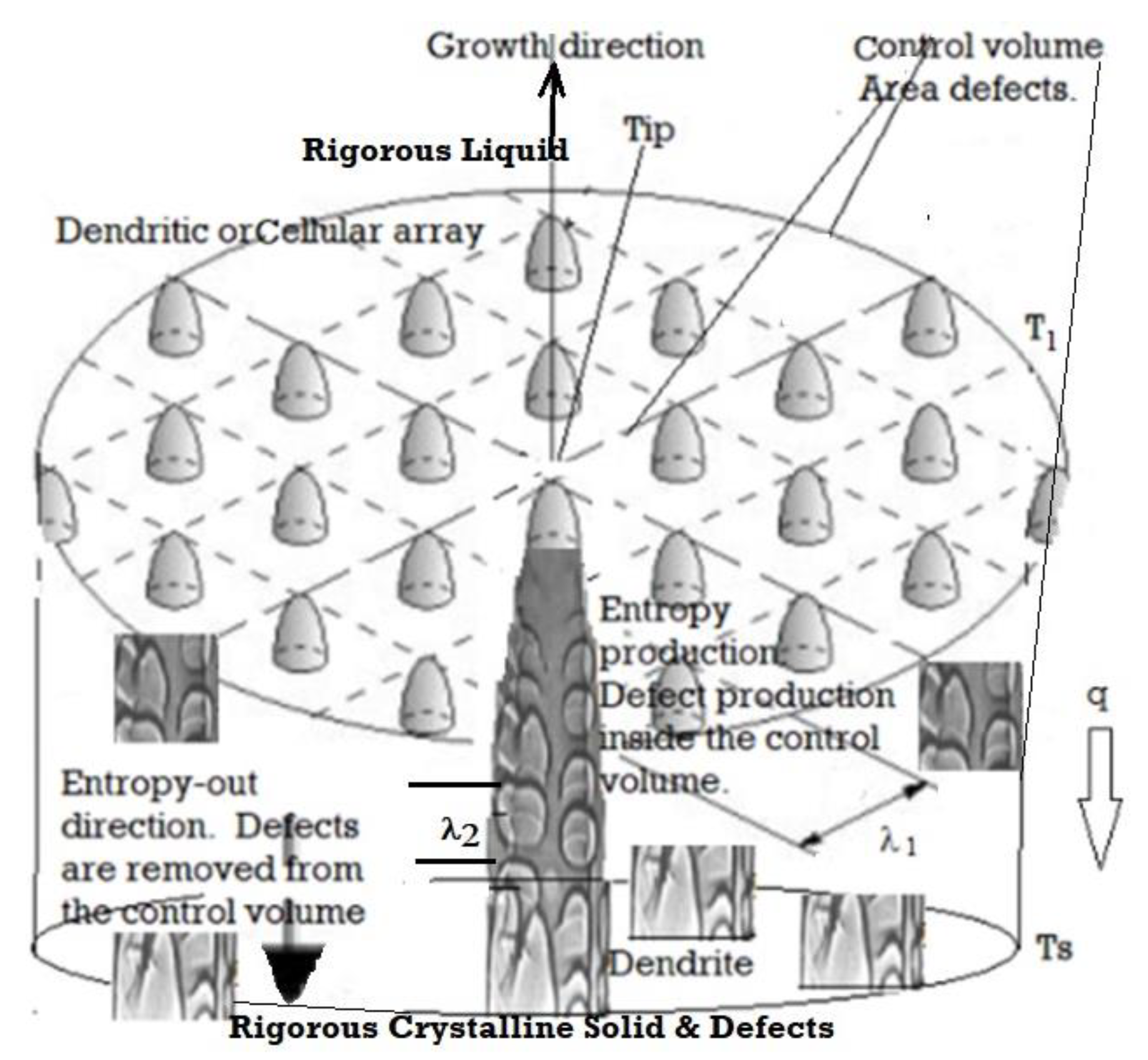
4.2. Medium Velocity Transitions: Cells, Cellular-Dendrites, and Dendrites
4.3. High-Velocity Regimes Including Featureless Solids and Metallic Glass
4.4. Range of Solidification Morphological Transitions
5. Discussions: The Utility of Self-Organization
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| Letter Symbols | |
| A | area of an interface in a solid-liquid region (m2) |
| ASD | surface area of the secondary dendrite features |
| d | interplanar lattice spacing (m) |
| ∆C0 | change in concentration for the liquid from the position of rigorous liquid to the bulk. ∆Co = (Cl* − Cs*) where Cl* and Cs* are the composition of the local rigorous-liquid and solid, respectively |
| D | diffusion coefficient (m2·s−1) |
| f | facet |
| F | is the friction force (kg·ms−2) |
| GSLI | gradient across a diffuse interface (K·m−1) |
| Gl | temperature gradient in the liquid or supercooling liquid (K·m−1) |
| Δhm | heat of fusion of a solid with defects (J·m−3) |
| Δhsl | heat of fusion (J·m−3) |
| H | hardness (J·m−3 or MPa) |
| Js | solute flux in a liquid entering a solid-liquid interface (mole·s−1) |
| k | equilibrium partition coefficient obtained from the phase diagram (dimensionless) |
| keff | effective partition coefficient at a solid-liquid interface (dimensionless)—a function of the velocity and diffuse interface structure |
| ΔKE | gain or loss in kinetic energy (J) |
| KL | thermal conductivity for a rigorous liquid (J·m−1·K−1·s−1) |
| KS | thermal conductivity for a rigorous solid (J·m−1·K−1·s−1) |
| Kav | average thermal conductivity in the control volume (J·m−1·K−1·s−1) |
| Kwear | wear constant, dimensionless ~10−4 for metal pairs. |
| Lo | sliding distance (length of object in Appendix A, in the direction of travel) |
| mL | slope of the equilibrium liquidus at the SLI for a binary material (K·m3·mole−1) |
| ms | slope of the equilibrium solidus line at the SLI for a binary material (K·m3·mole−1) |
| MEPR | maximum entropy production rate per unit volume (J·m−3·K−1·s−1) |
| MS | Mullins and Sekerka criterion [44] |
| Np | normal force (kg·m·s−2) |
| nf | non-facet |
| Rg | molar gas constant (J·mol−1·K−1) |
| RRMS | RMS height (m) |
| Sf | Entropy flux rate (J·K−1·s−1) to and from a solid-liquid interface with its surrounding |
| dSgen/dt | entropy generation rate in a diffuse region (J·K−1·s−1) |
| dSin/dt | rate of entropy entering a control volume (J·K−1·s−1) |
| dSout/dt | rate of entropy leaving a control volume (J·K−1·s−1) |
| dsgen/dt | entropy produced/generated rate density (J·m−3·K−1·s−1) |
| SLG | entropy generation rate density by the solute gradient in a liquid (J·m−3·Ks−1) |
| (Sgen)max | maximum entropy generation (J·K−1) |
| dScv/dt | total steady state entropy rate in a control volume (J·K−1·s−1) |
| dscv/dt | total steady state entropy rate density in a control volume ((J·K−1·s−1·m−3) |
| t | time (s) |
| SLI | solid-liquid interface |
| SD | side-branch secondary structures, such as secondary dendrites. |
| q1/τ | the heat transfer rate to the main body in a friction pair. |
| Tli | liquidus interface temperature at a rigorous liquid interface (K); generally assumed to be Tl (the equilibrium liquidus temperature) |
| Tsi | solidus interface temperature at a rigorous solid interface (K); generally assumed to be Ts (the equilibrium solidus or eutectic temperature) |
| Tctip | tip temperature of a cell |
| Ttip | tip temperature of cells, dendrites, or facets in an array |
| Ti | friction interface temperature of a friction pair |
| T0 | room temperature for the friction problem |
| Ti | friction interface temperature of a friction pair |
| Tm | melting temperature (K) of the pure metal or species |
| Tav | average temperature between Tli and Tsi in diffuse interface or solid-liquid region (K), when G is negative or close to zero |
| T0 | room temperature (ambient) |
| ΔTSLI | temperature difference across a solid-liquid interface (K) |
| ΔTctip(C−D)) = Tctip − Ts) (K) | at the cell or cellular dendrite transition to a dendrite |
| (dclG/dz) or (ΔCO/δc) | change in solute gradient in a liquid (mole·m−4) |
| ΔTO | solidification temperature range (K) = −mL·ΔCo(1/k − 1) |
| ΔTi | temperature difference between rigorous liquid and rigorous solid (K) = Tli − Tsi |
| ΔTctip | (Tctip − Ts) (K) |
| V | solidification interface velocity (ms−1) |
| V | sliding pair velocity (ms−1) (see Appendix A) |
| WL | lost work (J) |
| W | work (J) |
| Greek symbols | |
| ΔΩS | volume shrinkage (m3) |
| β | the autocorrelation length (m) of the surface |
| |Δρk| | density shrinkage (kg·m−3) |
| ρl | density of rigorous liquid (kg·m−3) |
| ρs | density of rigorous solid (kg·m−3) |
| γgb | solid-solid boundary energy (e.g., between primary cells or primary dendrites) |
| λ1 | primary spacing at the Ts isotherm |
| λ2 | secondary spacing at the Ts isotherm |
| λ2(C−D) | secondary spacing at the Ts isotherm for the conditions of cell, to dendrite transition |
| Δμc | chemical potential difference (J·mole−1) |
| Γ | boundary capillarity constant γgb/Δssl. |
| μ | coefficient of friction |
| θ | fraction of energy transferred to heat. |
| ζ | solid-liquid interface thickness (m), i.e., the diffuse interface thickness |
| ζg | is the zone thickness between Tl and Tg |
| ξ | wear volume |
| τ | (length of travel, Lo)/V (s) |
| ζ3cv | thermal control volume for steady state friction (Appendix A) |
| ωD | energy of defects (J·m−3) other than area defects |
| maximum entropy generation rate density for a moving interface (control volume) (J·m−3·K−1·s−1) | |
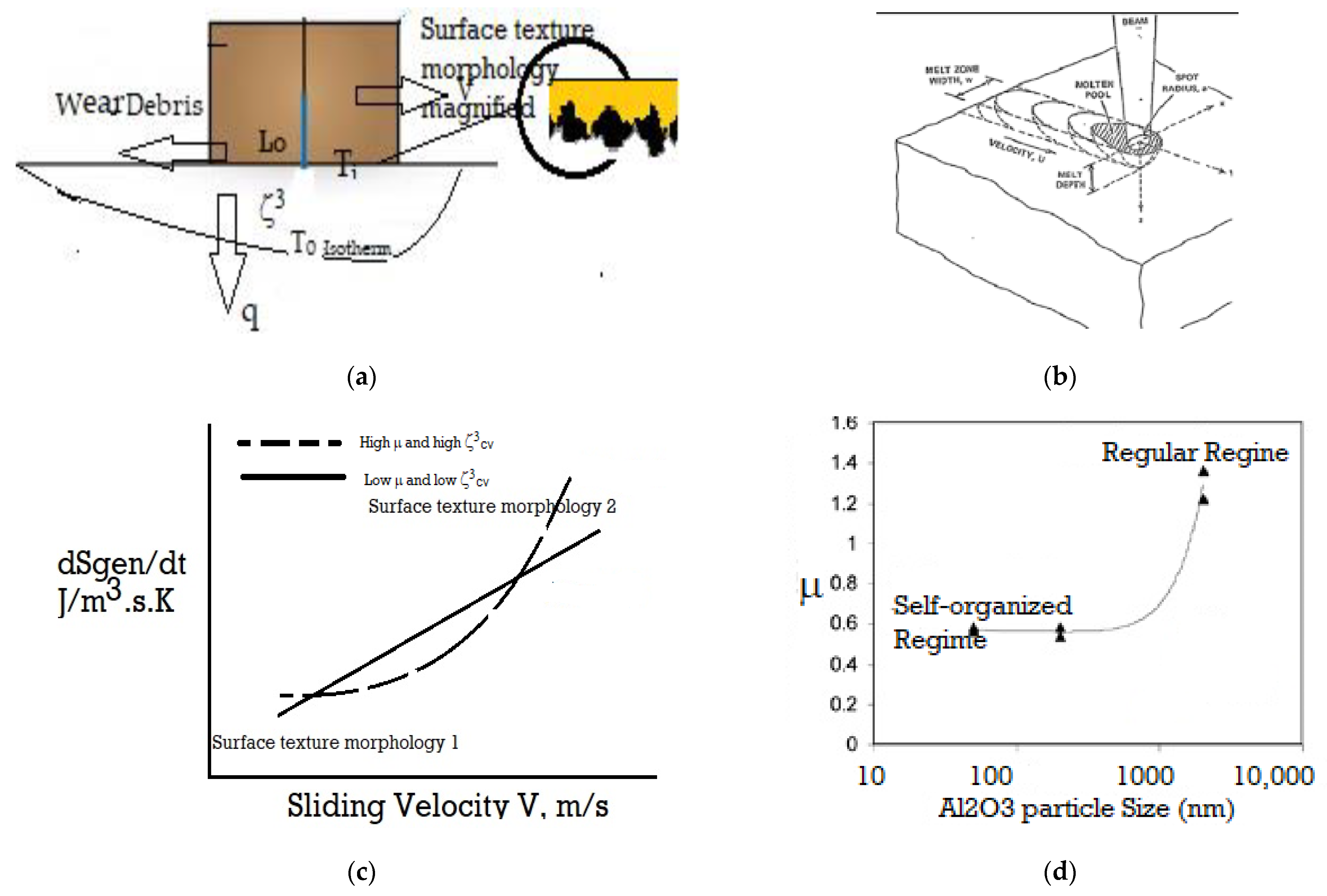
Appendix A. Self-Organization of Surface Texture during Friction and Wear
= (∫cv K·(ΔT/T)2) dζ3)/(ζ3cv) + ω/Ti/(ζ3cv)
References
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN-10:0471973947. [Google Scholar]
- Sekhar, J.A. The description of morphologically stable regimes for steady state solidification based on the maximum entropy production rate postulate. J. Mater. Sci. 2011, 46, 6172–6190. [Google Scholar] [CrossRef]
- Martyushev, L.M. Maximum entropy production principle: History and current status. Uspekhi Fiz. Nauk 2021, 64, 586–613. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Energy, Information, Feedback, Adaptation, and Self-Organization, Intelligent Systems, Control and Automation: Science and Engineering 90; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Pave, A.; Schmidt-Lainé, C. Integrative Biology: Modelling and Simulation of the Complexity of Natural Systems. Biol. Int. 2004, 44, 13–24. [Google Scholar]
- Fath, B. Encyclopedia of Ecology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Sekhar, J. Thermodynamics, Irreversibility and Beauty. Available online: https://encyclopedia.pub/9548 (accessed on 23 June 2021).
- Ballufi, R.W.; Allen, M.A.; Carter, W.C. Kinetics of Materials; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Wikipedia. Differential Entropy. Available online: https://en.wikipedia.org/wiki/Differential_entropy (accessed on 27 June 2021).
- Martyushev, L.M.; Zubarev, S.N. Entropy production of stars. Entropy 2015, 17, 3645–3655. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Birzina, A. Entropy production and stability during radial displacement of fluid in Hele-Shaw cell. J. Phys. Condens. Matter 2008, 20, 465102. [Google Scholar] [CrossRef]
- Turing, A.M. The molecular basis of morphogenesis. Philos. Trans. R. Soc. 1952, 37, 237. [Google Scholar]
- Bensah, Y.D.; Sekhar, J.A. Solidification Morphology and Bifurcation Predictions with the Maximum Entropy Production Rate Model. Entropy 2020, 22, 40. [Google Scholar] [CrossRef]
- Heylighen, F. The Science of Self-Organization and Adaptivity, Center; Free University of Brussels: Brussels, Belgium, 2001; p. 9. [Google Scholar]
- Sánchez-Gutiérrez, D.; Tozluoglu, M.; Barry, J.D.; Pascual, A.; Mao, Y.; Escuder, L.M. Fundamental physical cellular constraints drive self-organization of tissues. EMBO J. 2016, 35, 77–88. [Google Scholar] [CrossRef]
- Lucia, U. Maximum entropy generation and K-exponential model. Phys. A Stat. Mech. Appl. 2010, 389, 4558–4563. [Google Scholar] [CrossRef]
- Hill, A. Entropy production as the selection rule between different growth morphologies. Nature 1990, 348, 426–428. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D.; Kuznetsova, I.E. Application of the Principle of Maximum Entropy production to the analysis of the morphological stability of a growing crystal. Zh. Éksp. Teor. Fiz. 2000, 118, 149. [Google Scholar]
- Ziman, J.M. The general variational principle of transport theory. Can. J. Phys. 1956, 35, 1256. [Google Scholar] [CrossRef]
- Kirkaldy, J.S. Entropy criteria applied to pattern selection in systems with free boundaries. Metall. Trans. A 1985, 16, 1781–1796. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Ziegler, H.; Wehrli, C. On a principle of maximal rate of entropy production. J. Non-Equilib. Therm. 1978, 12, 229. [Google Scholar] [CrossRef]
- Trivedi, R.; Somboonsuk, K. Constrained Dendritic Growth and Spacing. Mater. Sci. Eng. 1984, 65, 65–74. [Google Scholar] [CrossRef]
- Flemings, M.C. Solidification Processing; McGraw Hill: New York, NY, USA, 1974. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans Tech Publications: Aedermannsdorf, Switzerland, 1989. [Google Scholar]
- Mehrabian, R.; Kear, B.H.; Cohen, M. Rapid Solidification Processing. Principles and Technologies, II. In Proceedings of the 2nd International Conference on Rapid Solidification Processing, Reston, VA, USA, 23–26 March 1980; Claitor’s Publishing Division: Baton Rouge, LA, USA, 1980; pp. 153–164. [Google Scholar]
- Tsallis, C. Nonadditive entropy: The concept and its use, Theoretical Physics. Eur. Phys. 2009, 40, 257–266. [Google Scholar] [CrossRef]
- Haitao, Y.; Jiulin, D. Entropy Production Rate of Nonequilibrium Systems from the Fokker-Planck Equation. Available online: https://arxiv.org/ftp/arxiv/papers/1406/1406.4453.pdf (accessed on 15 June 2021).
- Schnakenberg, J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys. 1976, 48, 571. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Structure, Stabilité et Fluctuations; Wiley-Interscience: Paris, France, 1971. [Google Scholar]
- Sekhar, J.A.; Li, H.P.; Dey, G.K. Decay-dissipative Belousov–Zhabotinsky nanobands and nanoparticles in NiAl. Acta Mater. 2010, 58, 1056–1073. [Google Scholar] [CrossRef]
- Shohoji, N. Roles of Unstable Chemical Species and Non-Equilibrium Raction Routes on Properties of Reaction Product—A review. J. Surf. Interfaces Mater. 2014, 2, 182–205. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Servio, P.; Ray, A.D. Rate of Entropy Production in Evolving Interfaces and Membranes under Astigmatic Kinematics: Shape Evolution in Geometric-Dissipation Landscapes. Entropy 2020, 22, 909. [Google Scholar] [CrossRef]
- Bilal, S. Finite element simulations for Entropy Generation. In Review. 2020. [Google Scholar] [CrossRef]
- Utter, B.; Bodenschatz, E. Double Dendrite Growth in Solidification, August. Phys. Rev. 2005, 72, 011601. [Google Scholar] [CrossRef]
- Trivedi, R.; Sekhar, J.A.; Seetharaman, V. Solidification Microstructures near the Limit of Absolute Stability. Met. Trans. A 1989, 20, 769–777. [Google Scholar] [CrossRef]
- Fabietti, L.M.; Sekhar, J.A. Planar to Equiaxed Transition in the Presence of an External Wetting Surface. Metall. Trans. 1992, 23, 3361–3368. [Google Scholar] [CrossRef]
- Fabietti, L.M.; Sekhar, J.A. Quantitative microstructure maps for restrained directional growth. J. Mater. Sci. 1994, 19, 473–477. [Google Scholar] [CrossRef]
- Jones, H. The status of rapid solidification of alloys in research and application. J. Mater. Sci. 1984, 19, 1043–1076. [Google Scholar] [CrossRef]
- Klement, W.; Willens, R.H.; Duwez, R. Non-crystalline structure in solidified gold–silicon alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Shangguan, D.; Hunt, J.D. In situ observation of faceted cellular array growth. Metall Mater Trans A. 1991, 22, 941–945. [Google Scholar] [CrossRef]
- Dey, N.; Sekhar, J.A. Interface Configurations during the directional growth of Salol-1 Morphology. Acta Metall. Mater. 1993, 41, 409–424. [Google Scholar] [CrossRef]
- Biloni, H.; Boettinger, W.J. Solidification. In Physical Metallurgy, 4th ed.; Cahn, R.W., Haasen, P., Eds.; Elsevier: Amsterdam, The Netherlands, 1996; pp. 669–842. [Google Scholar]
- Mullins, W.W.; Sekerka, R.F. Stability of a Planar Interface during Solidification of a Dilute Binary Alloy. J. Appl. Phys. 1964, 35, 444. [Google Scholar] [CrossRef]
- Sekhar, J.A. Laser Materials. Interaction. Ph.D. Thesis, University of Illinois, Urbana-Champaign, IL, USA, 1982. [Google Scholar]
- Glicksman, M.; Ankit, K. Thermodynamic behavior of solid-liquid grain boundary grooves. Philos. Mag. 2020, 100, 1789–1817. [Google Scholar] [CrossRef]
- Baker, J.C.; Cahn, J.W. Thermodynamics of Solidification. In Solidification; ASM: Materials Park, OH, USA, 1971; p. 21. [Google Scholar]
- Kolmogorov, A.N. Entropy per unit time as a metric invariant of automorphisms. Dokl. Akad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Sotolongo-Costa, O.; Rodriguez, I. Entropy variation in a fractal phase space. Acad. Lett. 2021, 662, 1–4. [Google Scholar] [CrossRef]
- Trelles, J.P. Pattern formation and self-organization in plasmas interacting with surfaces. J. Phys. D Appl. Phys. 2016, 49, 393002. [Google Scholar] [CrossRef]
- Kahn, D. Brain basis of self: Self-organization and lessons from dreaming. Front. Psychol. 2013, 4, 408. [Google Scholar] [CrossRef] [PubMed]
- Ivanitskii, G.R. Self-organizing dynamic stability of far-from-equilibrium biological systems. Physics-Uspekhi 2017, 60, 705. [Google Scholar] [CrossRef]
- Hiesinger, P.R. The Self-Assembling Brain: How Neural Networks Grow Smarter; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Nosonovsky, M. Entropy in Tribology: In the Search for Applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Nosonvsky, M.; Bhushan, B. Biomimetic superhydrophobic surfaces: Multiscale approach. Nano Lett. 2007, 7, 2633–2637. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, J.A. Tunable coefficient of friction with surface texturing in materials engineering and biological systems. Curr. Opin. Chem. Eng. 2018, 19, 94–106. [Google Scholar] [CrossRef]
- Sekhar, J.A.; Mantri, A.S.; Saha, S.; Balamuralikrishnan, R.; Rao, P.R. Photonic, Low-Friction and Antimicrobial Applications for an Ancient Icosahedral/Quasicrystalline Nano-composite Bronze Alloy. Trans. Indian Inst. Met. 2019, 72, 2105–2119. [Google Scholar] [CrossRef]
- De La Fuente, I.M.; Martínez, L.; Pérez-Samartín, A.L.; Ormaetxea, L.; Amezaga, C.; Vera-López, A. Global Self-Organization of the Cellular Metabolic Structure. PLoS ONE 2008, 3, e3100. [Google Scholar] [CrossRef] [PubMed]
- Blumenfeld, L.A.; Haken, H. Problems of Biological Physics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bensah, Y.D.; Sekhar, J.A. Morphological assessment with the maximum entropy production rate (MEPR) postulate. Curr. Opin. Chem. Eng. 2014, 3, 91–98. [Google Scholar] [CrossRef]
- Lin, C.S.; Sekhar, J.A. Solidification Morphology and semi-solid deformation in Superalloy Rene 108 (Part IV). J. Mater. Sci. 1994, 29, 5005–5013. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Prokopenko, M. Thermodynamic Efficiency of Interactions in Self-Organizing Systems. Entropy 2021, 23, 757. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear―A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Sista, B.; Vemaganti, K. Estimation of statistical parameters of rough surfaces suitable for developing micro-asperity friction models. Wear 2014, 316, 6–18. [Google Scholar] [CrossRef]
- Rao, K.V.R.; Sekhar, J.A. Surface solidification with a moving heat source, a study of solidification parameters. Acta Metall. 1987, 3, 81. [Google Scholar] [CrossRef]
- Basu, B.; Sekhar, J.A.; Schaefer, R.J.; Mehrabian, R. An analysis of the steady state molten pool obtained by heating a substrate with an electron beam. Acta Metall. Mater. 1991, 39, 725–733. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.J.; Lin, C.; Shi, F. Development of a set of Stribeck curves for conformal contacts of rough surfaces. Tribol. Trans. 2006, 49, 526–535. [Google Scholar] [CrossRef]
- Pasumarty, S.M.; Johnson, S.A.; Watson, S.A.; Adams, M.J. Friction of the human finger pad: Influence of moisture, occlusion and velocity. Tribol. Lett. 2011, 44, 117–137. [Google Scholar] [CrossRef]
- Chen, G.S. Handbook of Friction-Vibration; Woodhead Publishing: Sawston, UK, 2014. [Google Scholar]
- Gersham, L.; Gersham, E.I.; Mironov, A.E.; Fox-Rabinovich, G.S.; Veldhuid, S.C. Application of the self-organization phenomenon in the development of wear resistant materials—A Review. Entropy 2016, 18, 385. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Illiopolous, A.C.; Zastenker, G.N.; Zeleny, L.M.; Karakatsanis, L.P.; Riazanteseva, M.; Xenalis, M.N.; Pavlov, E.G. Sudying Complexity in Solar Wind Plasma During Shock Events. arXiv 2015, arXiv:1310.0525. [Google Scholar]
- Reis, A.H. Use and Validity of principles of extremum on entropy production in the study of complex systems. Ann. Phys. 2014, 346, 22–27. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Iliopoulos, A.C.; Karakatsanis, L.P.; Xenakis, M.; Pavlos, E. Complexity of Economical Systems, Special Issue on Econophysics. J. Eng. Sci. Technol. Rev. 2015, 8, 41–55. [Google Scholar] [CrossRef]
- Bensah, Y.D.; Sekhar, J.A. Interfacial instability of a planar interface and diffuseness at the solid-liquid interface for pure and binary materials. arXiv 2016, arXiv:1605.05005. [Google Scholar]
- Pontzer, H.; Brown, M.H.; Raichlen, D.A.; Dunsworth, H.; Hare, B.; Walker, K.; Luke, A.; Dugas, L.R.; Durazo-Arvizu, R.; Schoeller, D.; et al. Metabolic acceleration and the evolution of human brain size and life history. Nature 2016, 533, 390–392. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekhar, J.A. Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach. Entropy 2021, 23, 1092. https://doi.org/10.3390/e23081092
Sekhar JA. Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach. Entropy. 2021; 23(8):1092. https://doi.org/10.3390/e23081092
Chicago/Turabian StyleSekhar, Jainagesh A. 2021. "Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach" Entropy 23, no. 8: 1092. https://doi.org/10.3390/e23081092
APA StyleSekhar, J. A. (2021). Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach. Entropy, 23(8), 1092. https://doi.org/10.3390/e23081092




