Biometric Identification Systems with Noisy Enrollment for Gaussian Sources and Channels †
Abstract
:1. Introduction
2. System Model and Converted System
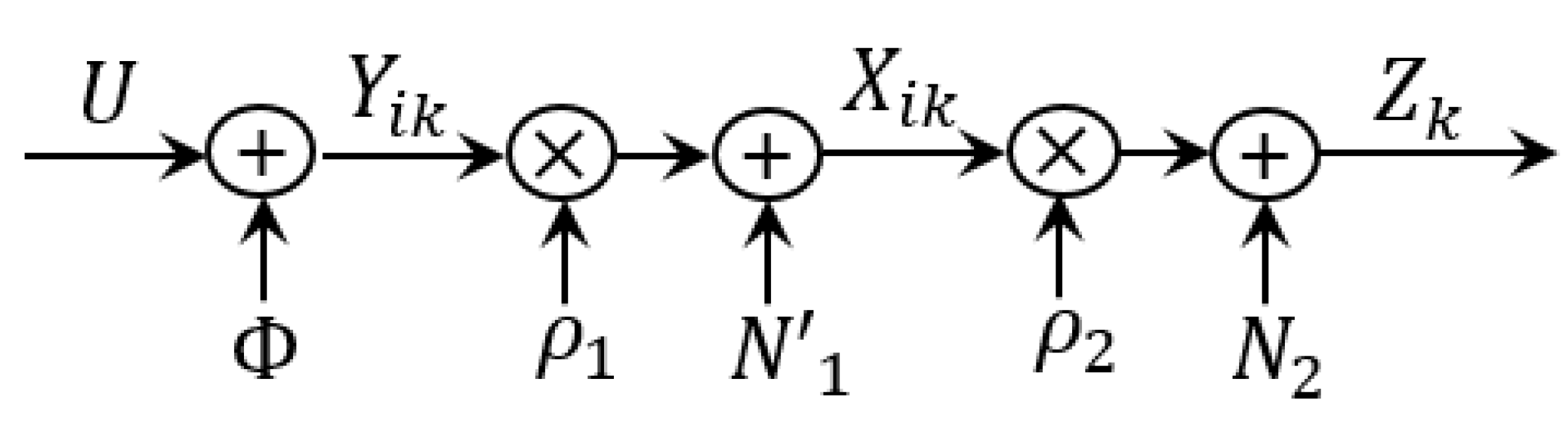
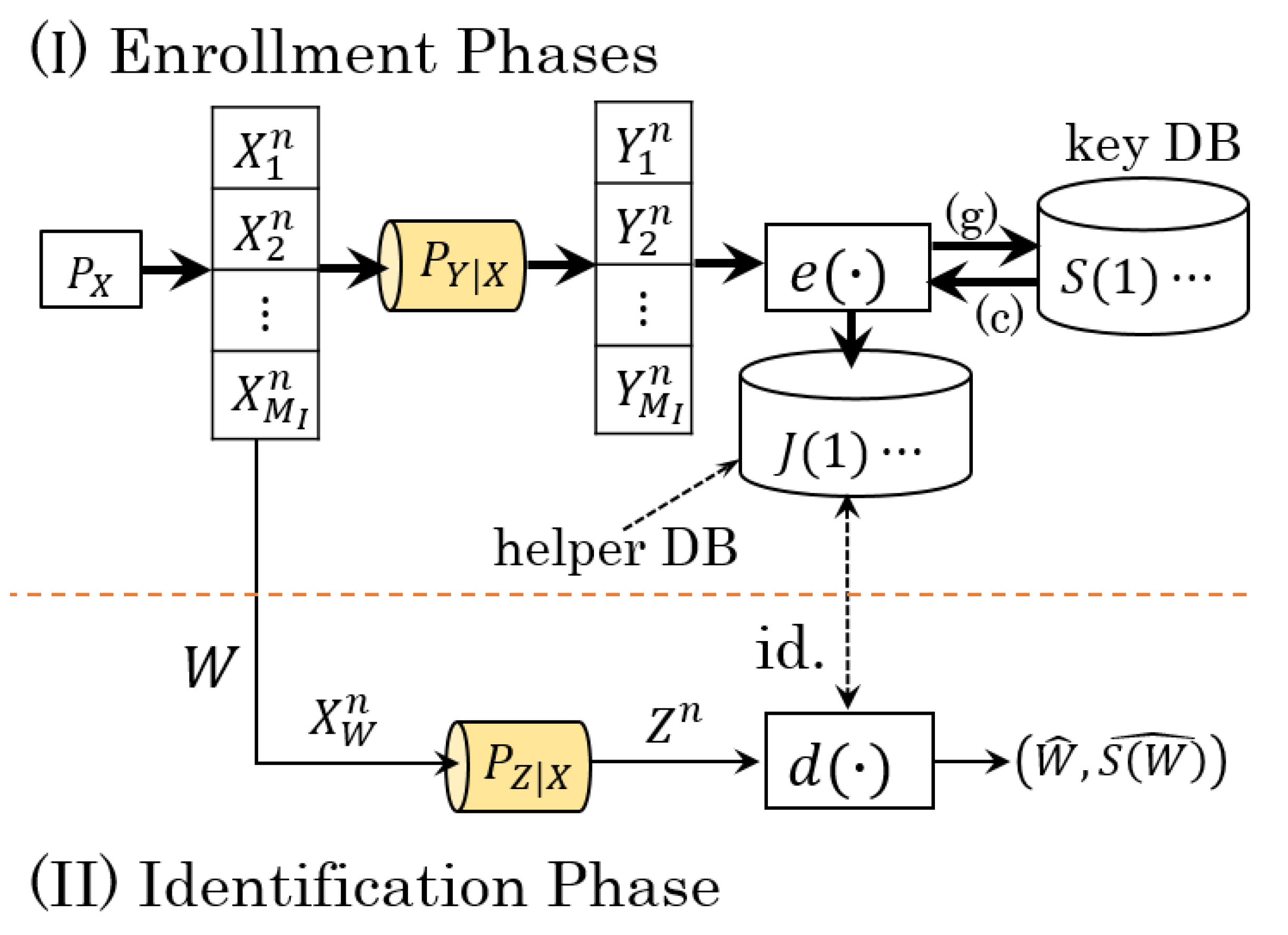
2.1. Notation and System Model
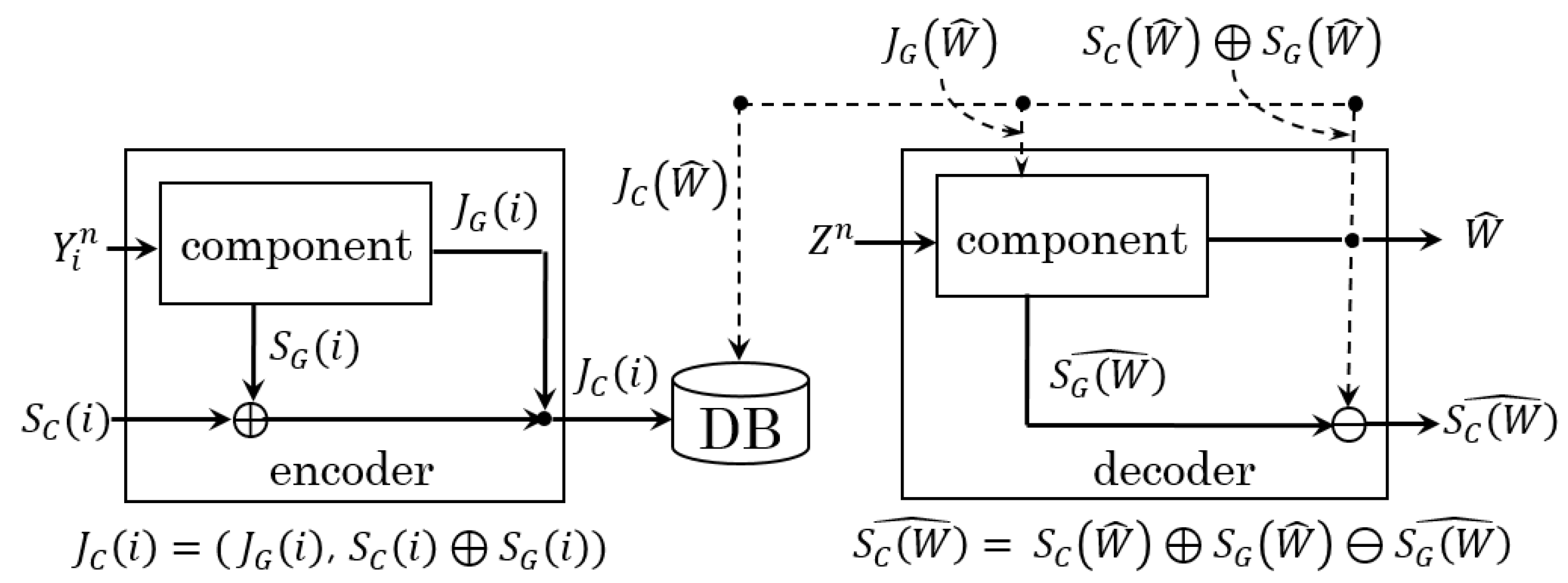
2.2. Converted System
3. Problem Formulation and Main Results
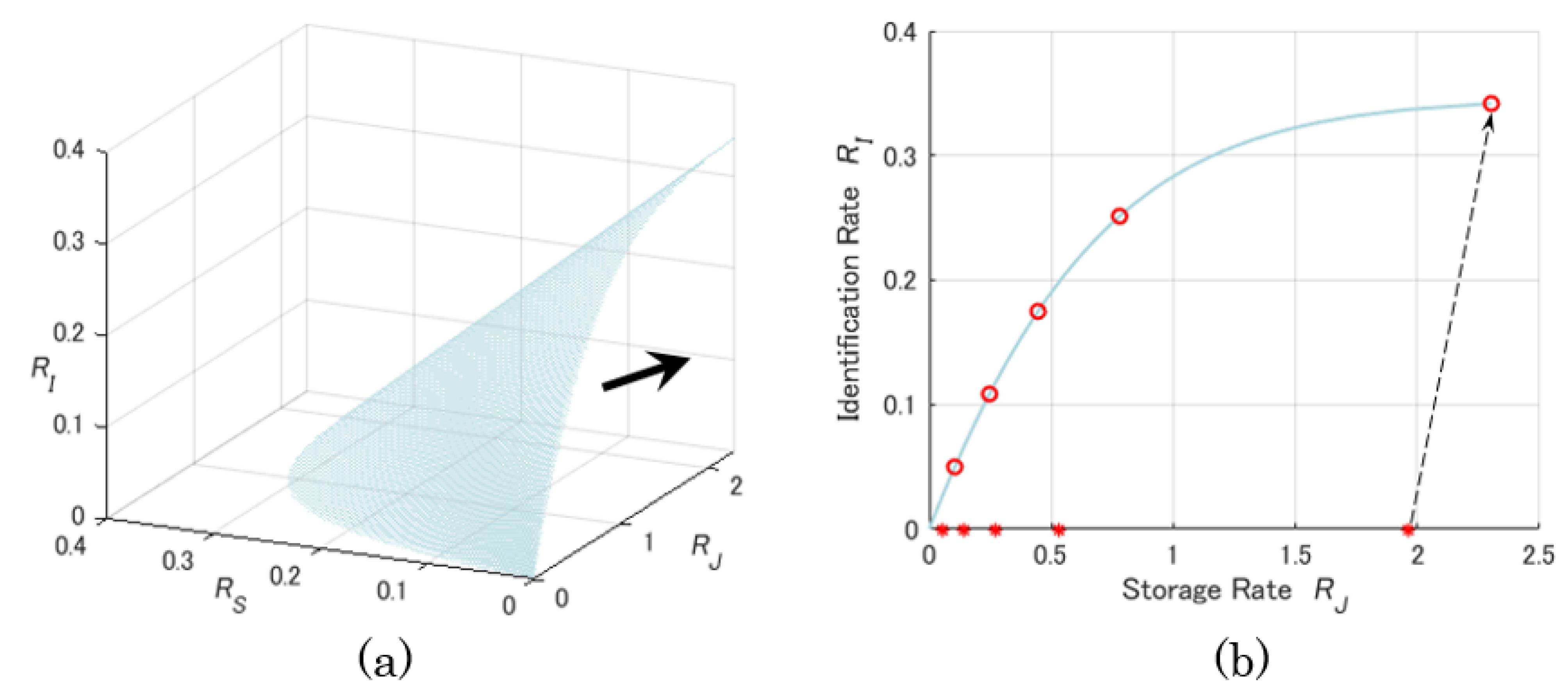
4. Behaviors of the Capacity Region
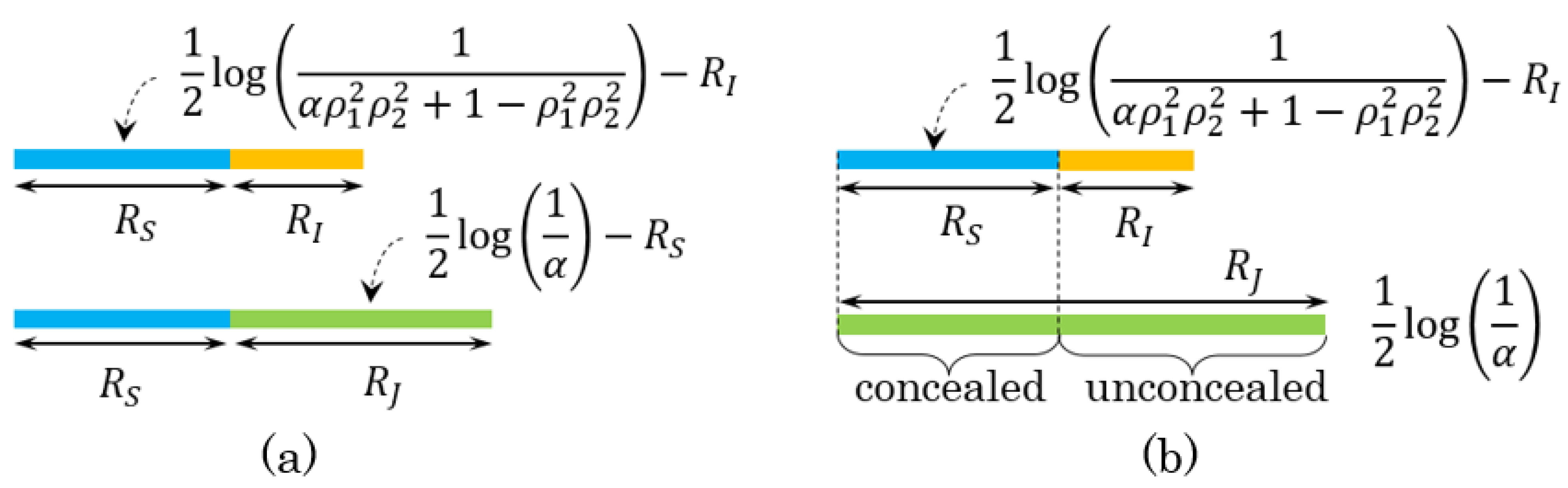
4.1. Optimal Asymptotic Rates and Zero-Rate Slopes
4.2. Examples
- Ex.1:
- (a) , (b) , (c) ,
- Ex.2:
- (a) , (b) , (c) ,
- Ex.3:
- (a) , (b) , (c) .
5. Overviews of the Proof of Theorem 1
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Equation (19)
Appendix A.1. Weakly Typical Sets and Modified Typical Sets
- 1
- For and large enough n,
- 2
- For , we have thatwhere denotes the volume of a set.
- 3
- Fix . If are independent sequences with the same marginals as , thenMoreover, for n large enough,
- Property 1.
- If then also .
- Property 2.
- Assume that . Then, for and n large enough, .
Appendix A.2. Achievability Part
- 1
- : { for all and },
- 2
- : {},
- 3
- : { for some },
- 4
- : { for some , and }.
- (c)
- follows as determines ,
- (d)
- follows because conditioning reduces entropy,
- (e)
- follows as , and we define ,
- (f)
- follows by applying Jensen’s inequality to the concave function ,
- (g)
- is due to (A17) in Lemma A3,
- (h)
- is due to (A3) in Lemma A1.
- (i)
- follows as and are functions of for given codebook ,
- (j)
- follows since are independent of , and the Markov chain holds,
- (k)
- follows because conditioning reduces entropy and is applied,
- (l)
- follows by applying Fano’s inequality since can be reliably reconstructed from for given codebook , and as and ,
- (m)
- is due to (A19).
Appendix A.3. Converse Part
- (a)
- holds since is a function of ,
- (b)
- follows because conditioning reduces entropy, and only is possibly dependent on ,
- (c)
- is due to Fano’s inequality with ,
- (d)
- follows since (A28) is applied, and W is independent of other RVs,
- (e)
- follows because conditioning reduces entropy.
- (f)
- holds as W is independent of ,
- (g)
- holds as W is independent of other RVs and is a function of ,
- (h)
- follows because , and by combining (A30) and (A31), we obtain that .
- (i)
- holds as W is independent of ,
- (j)
- follows because , and the same reason of (h) in (A33) is used.
Appendix B. Proof Sketch of Equation (20)
Appendix B.1. Achievability Part
Appendix B.2. Converse Part
- (a)
- follows since is a function of ,
- (b)
- follows as W is independent of other RVs and is chosen independently of ,
- (c)
- follows because (A40) is applied.
Appendix C. Convexity of the Regions and
- (a)
- follows as is a concave function,
- (b)
- holds as we define .
References
- Luis-Garcia, R.; Alberola-Lopez, C.; Aghzout, O.; Ruiz-Alzola, J. Biometric identification systems. Signal Proces. 2003, 83, 2539–2557. [Google Scholar] [CrossRef]
- Jain, A.K.; Flynn, P.; Ross, A. Handbook of Biometrics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Schneier, B. Inside risks: The uses and abuses of biometrics. Commun. ACM 1999, 42, 136. [Google Scholar] [CrossRef]
- Csisźar, I.; Narayan, P. Common randomness and secret key generation with a helper. IEEE Trans. Inf. Theory 2000, 46, 344–366. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Kalker, T.; Baggen, S.; Linnartz, J.P. On the capacity of a biometric identification system. In Proceedings of the 2003 IEEE International Symposium on Information Theory (ISIT), Yokohama, Japan, 29 June–4 July 2003; p. 82. [Google Scholar]
- Berger, T. Rate Distortion Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1971. [Google Scholar]
- Csiszár, I.; Köner, J. Information Theory—Coding Theorems for Discrete Memoryless Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Günlü, O.; Kramer, G. Privacy, Secrecy, and storage with multiple noisy measurements of identifiers. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2872–2883. [Google Scholar] [CrossRef] [Green Version]
- Tuncel, E. Capacity/Storage tradeoff in high-dimensional identification systems. IEEE Trans. Inf. Theory 2009, 55, 2097–2106. [Google Scholar] [CrossRef]
- Tuncel, E.; Gündüz, D. Identification and lossy reconstruction in noisy databases. IEEE Trans. Inf. Theory 2014, 60, 822–831. [Google Scholar] [CrossRef]
- Ignatenko, T.; Willems, F.M.J. Fundamental limits for privacy-preserving biometric identification systems that support authentication. IEEE Trans. Inf. Theory 2015, 61, 5583–5594. [Google Scholar] [CrossRef] [Green Version]
- Kittichokechai, K.; Caire, G. Secret key-based identification and authentication with a privacy constraint. IEEE Trans. Inf. Theory 2018, 64, 5879–5897. [Google Scholar] [CrossRef] [Green Version]
- Yachongka, V.; Yagi, H. A new characterization of the capacity region of identification systems under noisy enrollment. In Proceedings of the 54th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 18–20 March 2020. [Google Scholar]
- Yachongka, V.; Yagi, H. Identification, secrecy, template, and privacy-leakage of biometric identification system under noisy enrollment. arXiv 2019, arXiv:1902.01663. [Google Scholar]
- Zhou, L.; Vu, M.T.; Oechtering, T.J.; Skoglund, M. Two-stage biometric identification systems without privacy leakage. IEEE J. Sel. Areas Inf. Theory 2021, 2, 233–239. [Google Scholar] [CrossRef]
- Zhou, L.; Vu, M.T.; Oechtering, T.J.; Skoglund, M. Privacy-preserving identification systems with noisy enrollment. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3510–3523. [Google Scholar] [CrossRef]
- Ignatenko, T.; Willems, F.M.J. Biometric systems: Privacy and secrecy aspects. IEEE Trans. Inf. Forensics Security 2009, 4, 956–973. [Google Scholar] [CrossRef] [Green Version]
- Lai, L.; Ho, S.-W.; Poor, H.V. Privacy-security trade-offs in biometric security systems–part I: Single use case. IEEE Trans. Inf. Forensics Secur. 2011, 6, 122–139. [Google Scholar] [CrossRef]
- Koide, M.; Yamamoto, H. Coding theorems for biometric systems. In Proceedings of the 2010 IEEE International Symposium on Information Theory (ISIT), Austin, TX, USA, 13–18 June 2010; pp. 2647–2651. [Google Scholar]
- Günlü, O.; Kittichokechai, K.; Schaefer, R.F.; Caire, G. Controllable identifier measurements for private authentication with secret keys. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1945–1959. [Google Scholar] [CrossRef] [Green Version]
- Günlü, O. Multi-entity and multi-enrollment key agreement with correlated noise. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1190–1202. [Google Scholar] [CrossRef]
- Kusters, L.; Willems, F.M.J. Secret-key capacity regions for multiple enrollments with an SRAM-PUF. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2276–2287. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Ignatenko, T. Quantization effects in biometric systems. Proceeding of Information Theory and Applications Workshop, San Diego, CA, USA, 8–13 February 2009; pp. 372–379. [Google Scholar]
- Vu, M.T.; Oechtering, T.J.; Skoglund, M. Hierarchical identification with pre-processing. IEEE Trans. Inform. Theory 2020, 1, 82–113. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell System Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bergmans, P. A simple converse for broadcast channels with additive white Gaussian noise. IEEE Trans. Inf. Theory 1978, 20, 279–280. [Google Scholar] [CrossRef]
- Oohama, Y. Gaussian multiterminal source coding. IEEE Trans. Inf. Theory 1997, 43, 1912–1923. [Google Scholar] [CrossRef]
- Kittichokechai, K.; Oechtering, T.J.; Skoglund, M.; Chia, Y.K. Secure source coding with action-dependent side information. IEEE Trans. Inf. Theory 2015, 61, 6444–6464. [Google Scholar] [CrossRef]
- Weingarten, H.; Steinberg, Y.; Shamai (Shitz), S. The capacity region of the Gaussian MIMO broadcast channel. IEEE Trans. Inf.Theory 2006, 52, 3936–3964. [Google Scholar] [CrossRef]
- Ignatenko, T.; Willems, F.M.J. Privacy-leakage codes for biometric authentication systems. Proceeding of 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1601–1605. [Google Scholar]
- Yang, H.; Mihajlović, V.; Ignatenko, T. Private authentication keys based on wearable device EEG recordings. Proceeding of 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 956–960. [Google Scholar]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Bloch, M.; Barros, J. Physical-Layer Security; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]


| Cases | The Optimal Secret-Key Rate | Privacy-Leakage Rate | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (a) | (b) | (c) | |
| Ex. 1 | ||||||
| Ex. 2 | ||||||
| Ex. 3 | 0.14 | 0.09 | ||||
| Cases | The Slope of Secret-Key Rate | The Slope of Privacy-Leakage Rate | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (a) | (b) | (c) | |
| Ex. 1 | ||||||
| Ex. 2 | ||||||
| Ex. 3 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yachongka, V.; Yagi, H.; Oohama, Y. Biometric Identification Systems with Noisy Enrollment for Gaussian Sources and Channels. Entropy 2021, 23, 1049. https://doi.org/10.3390/e23081049
Yachongka V, Yagi H, Oohama Y. Biometric Identification Systems with Noisy Enrollment for Gaussian Sources and Channels. Entropy. 2021; 23(8):1049. https://doi.org/10.3390/e23081049
Chicago/Turabian StyleYachongka, Vamoua, Hideki Yagi, and Yasutada Oohama. 2021. "Biometric Identification Systems with Noisy Enrollment for Gaussian Sources and Channels" Entropy 23, no. 8: 1049. https://doi.org/10.3390/e23081049
APA StyleYachongka, V., Yagi, H., & Oohama, Y. (2021). Biometric Identification Systems with Noisy Enrollment for Gaussian Sources and Channels. Entropy, 23(8), 1049. https://doi.org/10.3390/e23081049






