Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microscopy and Single-Particle Tracking
2.2. Xenopus Extract Preparation and Modification
3. Results and Discussion
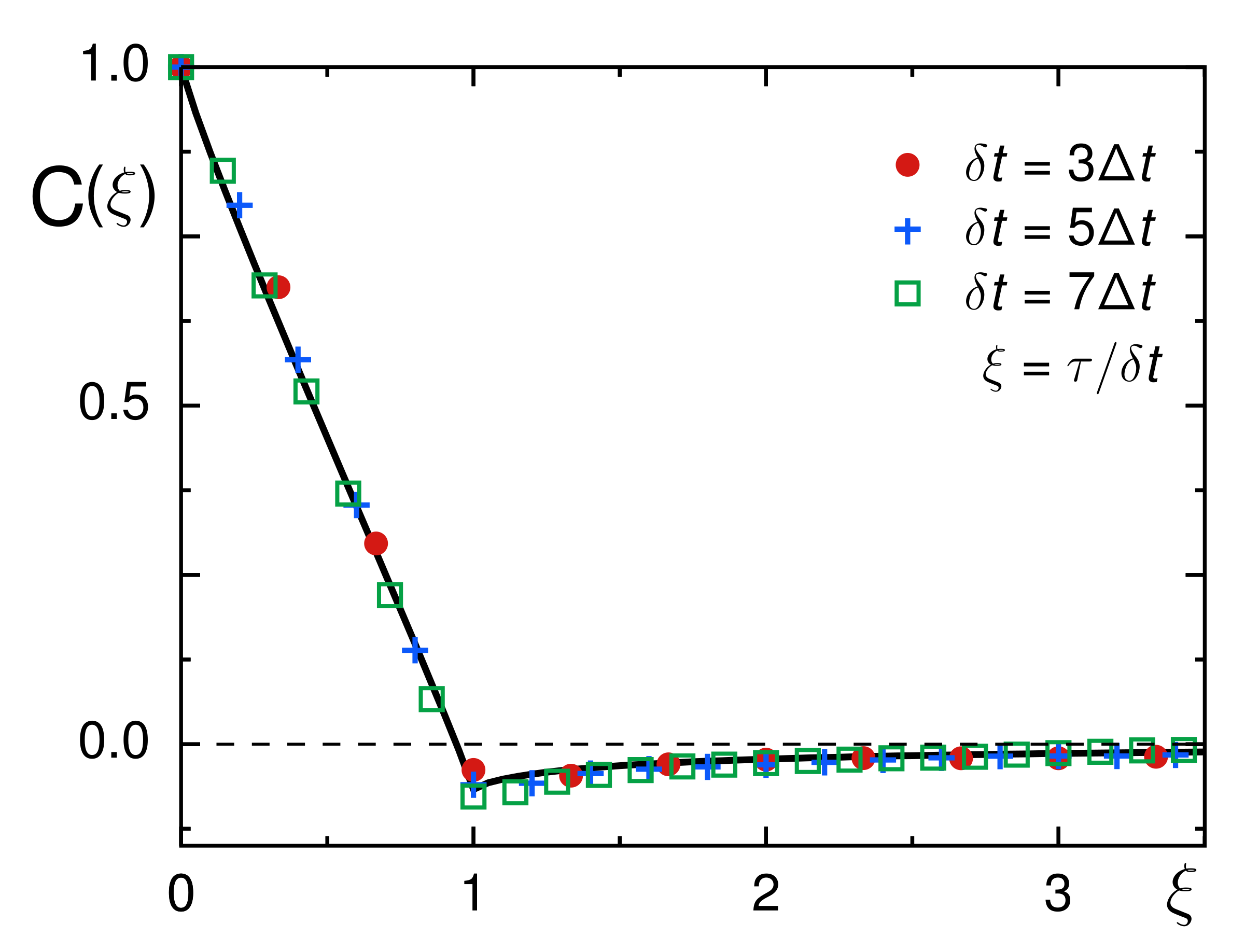
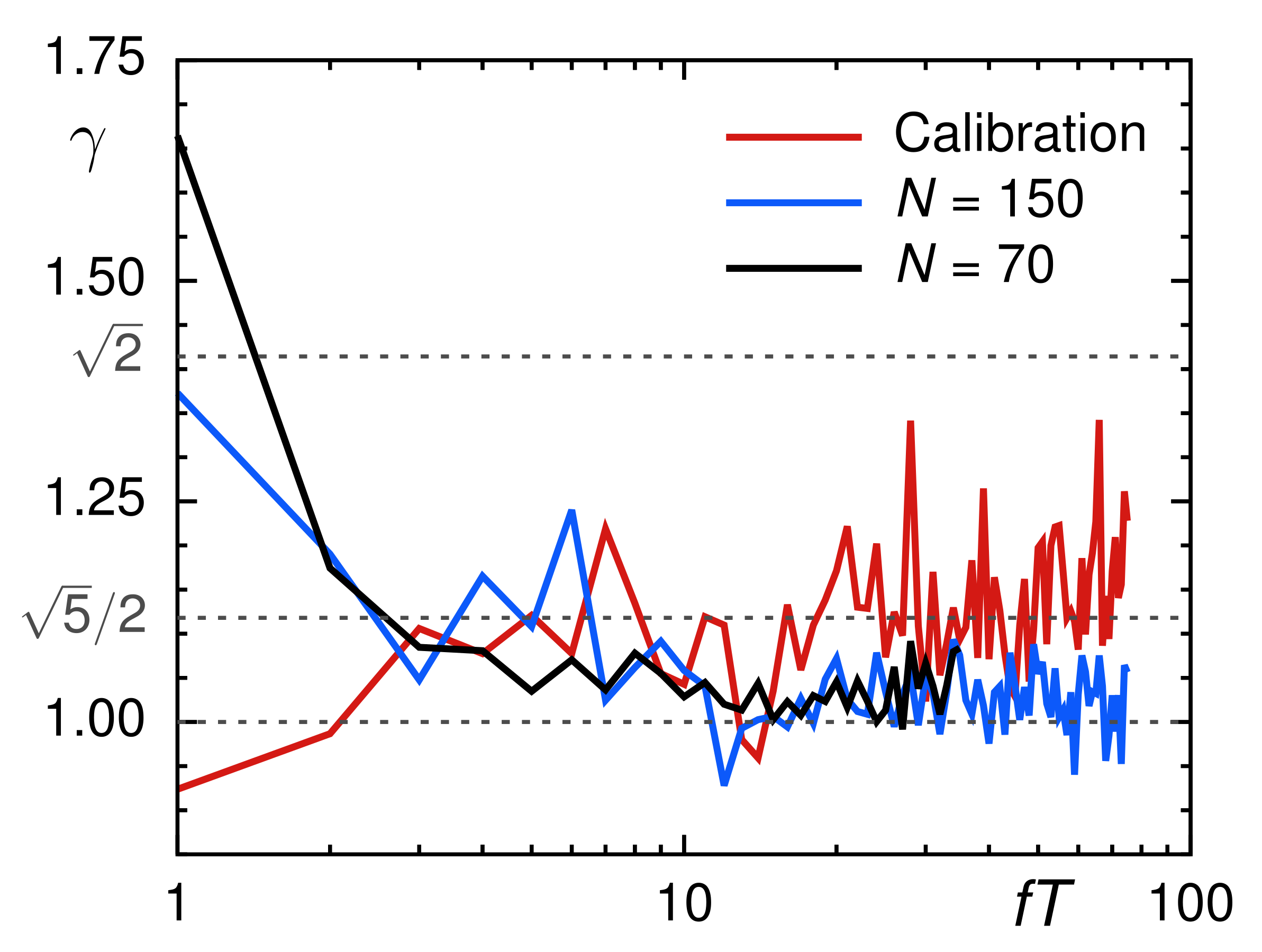
3.1. Calibration Experiments in Viscous Media
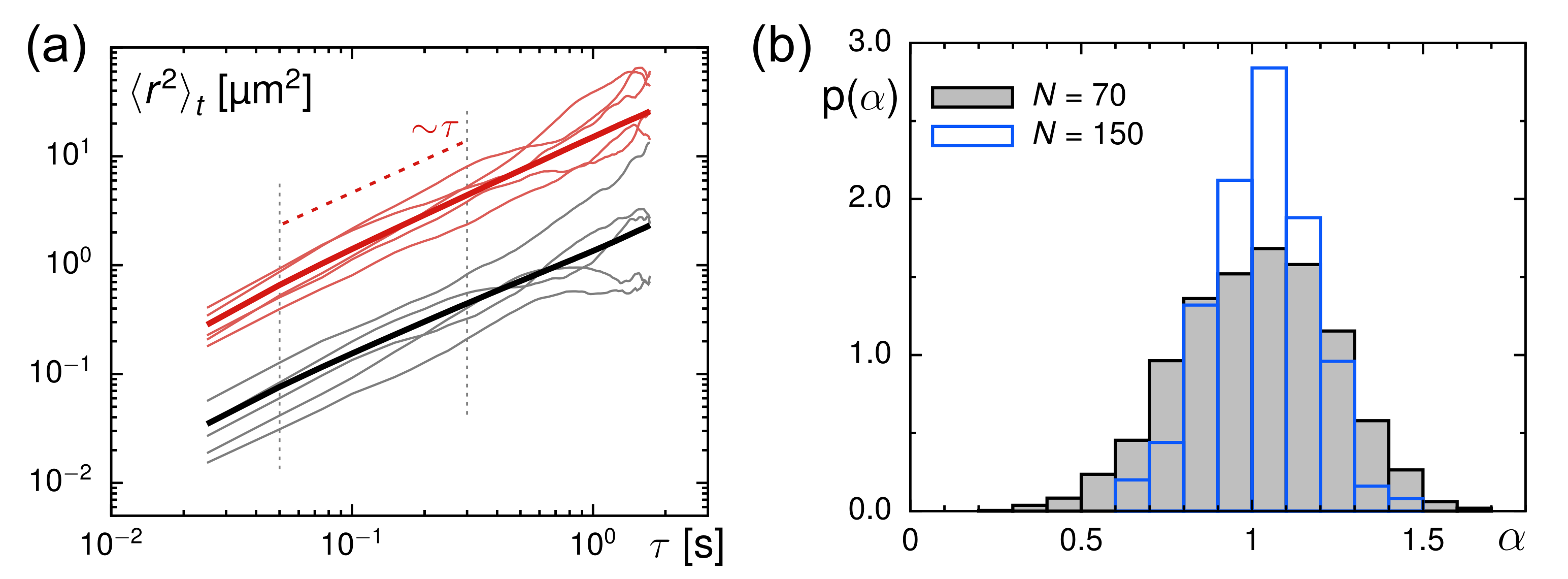
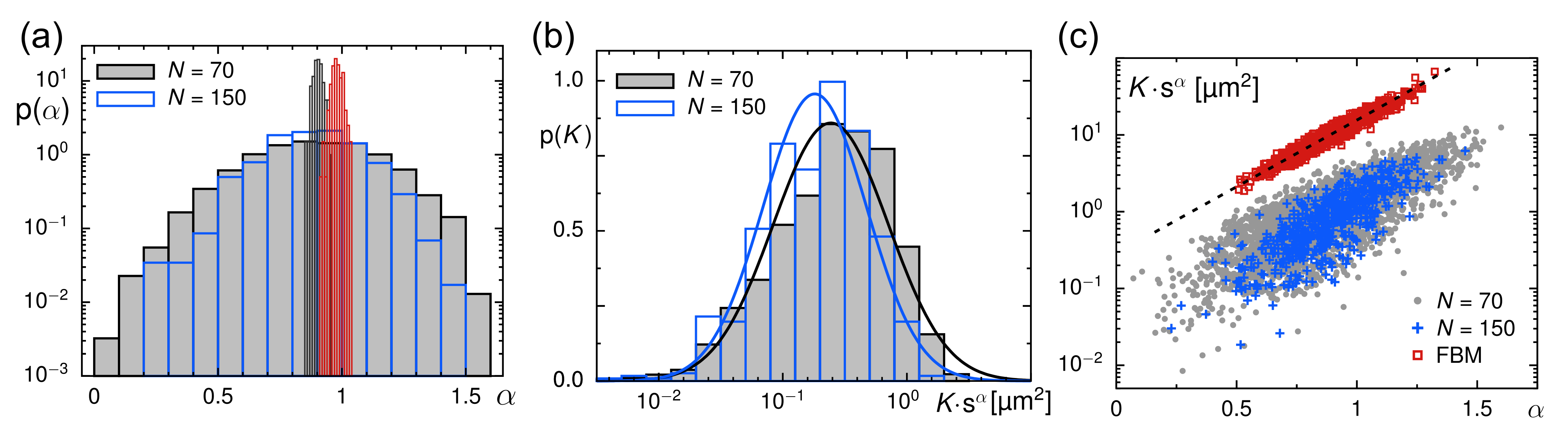
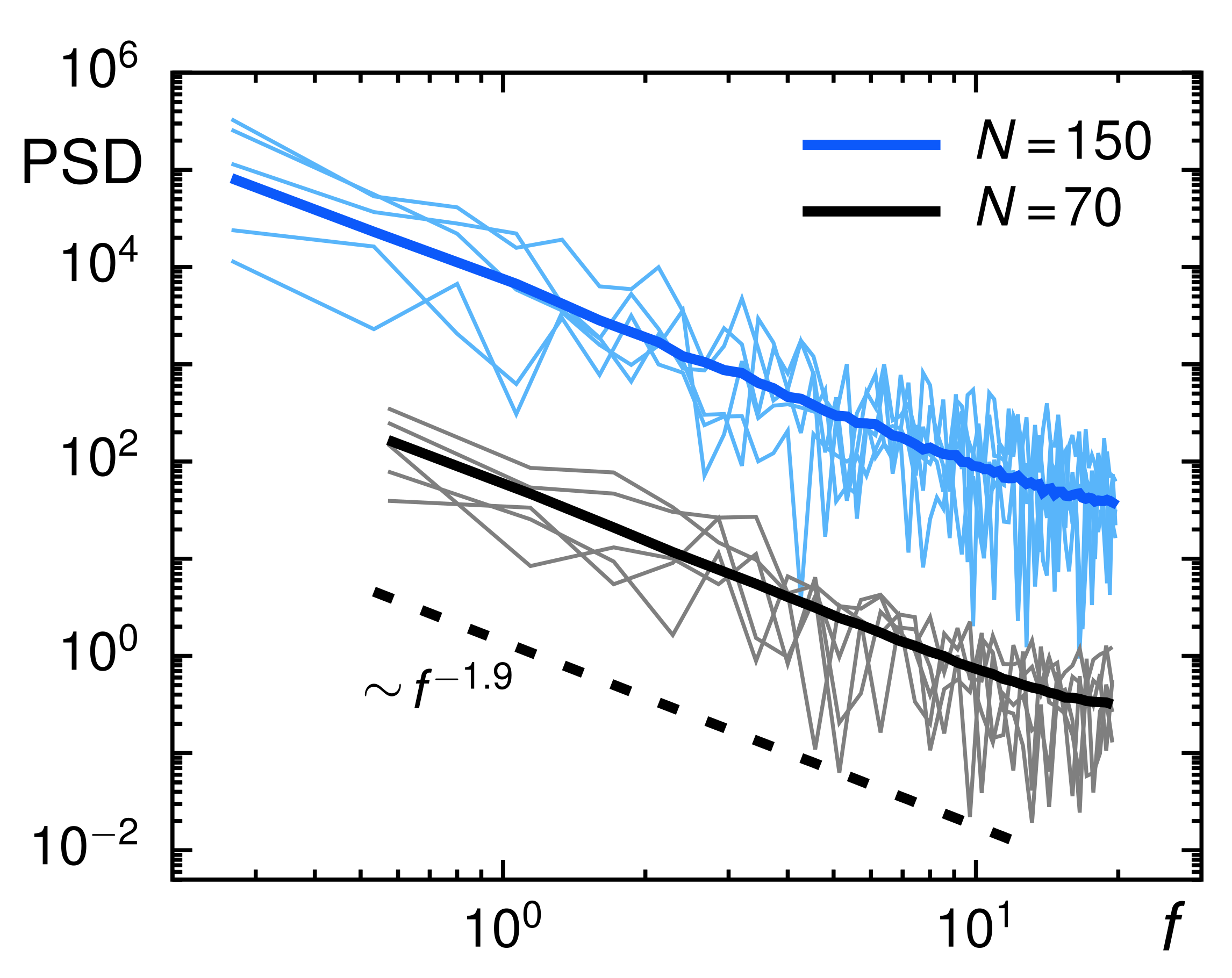
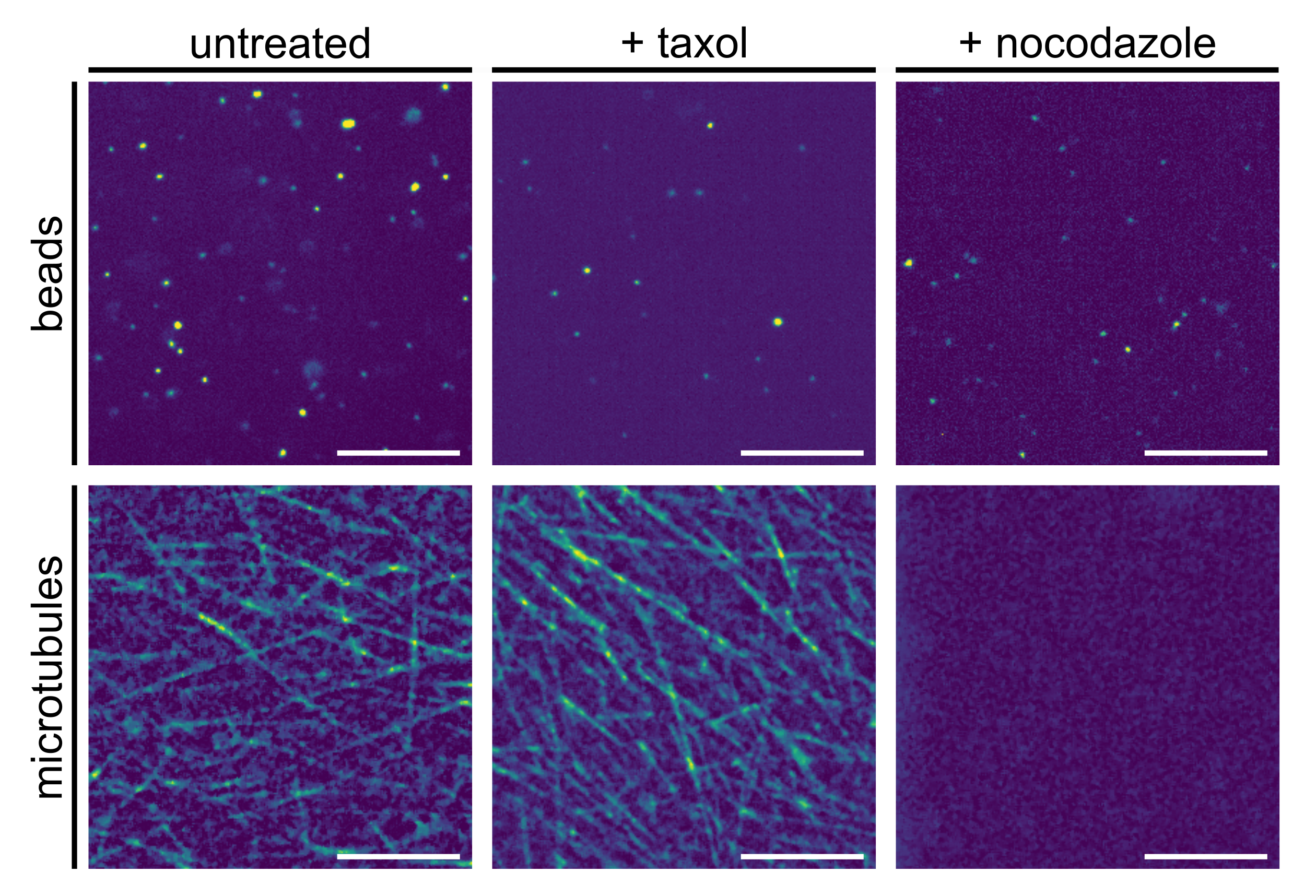
3.2. Evaluation of Tracer Motion in Native Xenopus Extract
3.3. From Native to Pharmaceutically Treated Xenopus Extracts
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, H.; Sheetz, M.P.P.; Elson, E.L.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef] [Green Version]
- Manzo, C.; Garcia-Parajo, M.F. A review of progress in single particle tracking: From methods to biophysical insights. Rep. Prog. Phys. 2015, 78, 124601. [Google Scholar] [CrossRef]
- Shen, H.; Tauzin, L.J.; Baiyasi, R.; Wang, W.; Moringo, N.; Shuang, B.; Landes, C.F. Single Particle Tracking: From Theory to Biophysical Applications. Chem. Rev. 2017, 117, 7331–7376. [Google Scholar] [CrossRef]
- Struntz, P.; Weiss, M. The hitchhiker’s guide to quantitative diffusion measurements. Phys. Chem. Chem. Phys. 2018, 20, 28910–28919. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Elsner, M.; Kartberg, F.; Nilsson, T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004, 87, 3518–3524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banks, D.; Fradin, C. Anomalous diffusion of proteins due to molecular crowding. Biophys. J. 2005, 89, 2960–2971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ernst, D.; Hellmann, M.; Köhler, J.; Weiss, M. Fractional brownian motion in crowded fluids. Soft Matter 2012, 8, 4886–4889. [Google Scholar] [CrossRef]
- Szymanski, J.; Weiss, M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys. Rev. Lett. 2009, 103, 038102. [Google Scholar] [CrossRef]
- Pan, W.; Filobelo, L.; Pham, N.D.; Galkin, O.; Uzunova, V.V.; Vekilov, P.G. Viscoelasticity in homogeneous protein solutions. Phys. Rev. Lett. 2009, 102, 1058101. [Google Scholar] [CrossRef]
- Guigas, G.; Kalla, C.; Weiss, M. Probing the nano-scale viscoelasticity of intracellular fluids in living cells. Biophys. J. 2007, 93, 316–323. [Google Scholar] [CrossRef] [Green Version]
- Weber, S.C.; Spakowitz, A.J.; Theriot, J.A. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys. Rev. Lett. 2010, 104, 238102. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.-H.; Tejedor, V.; Burov, S.; Barkai, E.; Selhuber-Unkel, C.; Berg-Sørensen, K.; Oddershede, L.; Metzler, R. In vivo anomalous diffusion and weak ergodicity breaking of lipid granules. Phys. Rev. Lett. 2011, 106, 048103. [Google Scholar] [CrossRef] [Green Version]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-Protein Particles Exhibit Non-Gaussian Subdiffusive Behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef] [Green Version]
- Sabri, A.; Xu, X.; Krapf, D.; Weiss, M. Elucidating the origin of heterogeneous anomalous diffusion in the cytoplasm of mammalian cells. Phys. Rev. Lett. 2020, 125, 058101. [Google Scholar] [CrossRef] [PubMed]
- Wachsmuth, M.; Waldeck, W.; Langowski, J. Anomalous diffusion of fluorescent probes inside living cell investigated by spatially-resolved fluorescence correlation spectroscopy. J. Mol. Biol. 2000, 298, 677–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pawar, N.; Donth, C.; Weiss, M. Anisotropic diffusion of macromolecules in the contiguous nucleocytoplasmic fluid during eukaryotic cell division. Curr. Biol. 2014, 24, 1905–1908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stadler, L.; Weiss, M. Non-equilibrium forces drive the anomalous diffusion of telomeres in the nucleus of mammalian cells. New J. Phys. 2017, 19, 113048. [Google Scholar] [CrossRef]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438–6443. [Google Scholar] [CrossRef] [Green Version]
- Malchus, N.; Weiss, M. Anomalous diffusion reports on the interaction of misfolded proteins with the quality control machinery in the endoplasmic reticulum. Biophys. J. 2010, 99, 1321–1328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeon, J.H.; Monne, H.M.S.; Javanainen, M.; Metzler, R. Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins. Phys. Rev. Lett. 2012, 109, 188103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stadler, L.; Speckner, K.; Weiss, M. Diffusion of exit sites on the endoplasmic reticulum: A random walk on a shivering backbone. Biophys. J. 2018, 115, 1552–1560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M. Crowding, diffusion, and biochemical reactions. Int. Rev. Cell Mol. Biol. 2014, 307, 383–417. [Google Scholar]
- Sokolova, E.; Spruijt, E.; Hansen, M.M.K.; Dubuc, E.; Groen, J.; Chokkalingam, V.; Piruska, A.; Heus, H.A.; Huck, W.T.S. Enhanced transcription rates in membrane-free protocells formed by coacervation of cell lysate. Proc. Natl. Acad. Sci. USA 2013, 110, 11692–11697. [Google Scholar] [CrossRef] [Green Version]
- Good, M.C.; Vahey, M.D.; Skandarajah, A.; Fletcher, D.A.; Heald, R. Cytoplasmic volume modulates spindle size during embryogenesis. Science 2013, 342, 856–860. [Google Scholar] [CrossRef] [Green Version]
- Hannak, E.; Heald, R. Investigating mitotic spindle assembly and function in vitro using xenopu s laevi s egg extracts. Nat. Protoc. 2006, 1, 2305. [Google Scholar] [CrossRef]
- Valentine, M.T.; Perlman, Z.E.; Mitchison, T.J.; Weitz, D.A. Mechanical properties of xenopus egg cytoplasmic extracts. Biophys. J. 2005, 88, 680–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- He, Y.; Burov, S.; Metzler, R.; Barkai, E. Random time-scale invariant diffusion and transport coefficients. Phys. Rev. Lett. 2008, 101, 058101. [Google Scholar] [CrossRef]
- Lubelski, A.; Sokolov, I.M.; Klafter, J. Nonergodicity mimics inhomogeneity in single particle tracking. Phys. Rev. Lett. 2008, 100, 250602. [Google Scholar] [CrossRef] [Green Version]
- Neusius, T.; Sokolov, I.M.; Smith, J.C. Subdiffusion in time-averaged, confined random walks. Phys. Rev. E 2009, 80, 011109. [Google Scholar] [CrossRef] [Green Version]
- Burov, S.; Metzler, R.; Barkai, E. Aging and nonergodicity beyond the khinchin theorem. Proc. Natl. Acad. Sci. USA 2010, 107, 13228–13233. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Tinevez, J.-Y.; Perry, N.; Schindelin, J.; Hoopes, G.M.; Reynolds, G.D.; Laplantine, E.; Bednarek, S.Y.; Shorte, S.L.; Eliceiri, K.W. Trackmate: An open and extensible platform for single-particle tracking. Methods 2017, 115, 80–90. [Google Scholar] [CrossRef]
- Jaqaman, K.; Loerke, D.; Mettlen, M.; Kuwata, H.; Grinstein, S.; Schmid, S.L.; Danuser, G. Robust single-particle tracking in live-cell time-lapse sequences. Nat. Methods 2008, 5, 695–702. [Google Scholar] [CrossRef] [Green Version]
- Dumont, S.; Mitchison, T.J. Force and length in the mitotic spindle. Curr. Biol. 2009, 19, R749–R761. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weiss, M. Resampling single-particle tracking data eliminates localization errors and reveals proper diffusion anomalies. Phys. Rev. E 2019, 100, 042125. [Google Scholar] [CrossRef] [PubMed]
- Kroese, D.P.; Botev, Z.I. Spatial Process Simulation. In Stochastic Geometry, Spatial Statistics and Random Fields; Schmidt, V., Ed.; Springer: Cham, Switzerland, 2015; Volume 2120, pp. 369–404. [Google Scholar]
- Wade, W.F.; Freed, J.H.; Edidin, M. Translational diffusion of class ii major histocompatibility complex molecules is constrained by their cytoplasmic domains. J. Cell Biol. 1989, 109, 3325–3331. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Single-particle tracking: The distribution of diffusion coefficients. Biophys. J. 1997, 72, 1744–1753. [Google Scholar] [CrossRef] [Green Version]
- Laurence, T.A.; Kwon, Y.; Yin, E.; Hollars, C.W.; Camarero, J.A.; Barsky, D. Correlation spectroscopy of minor fluorescent species: Signal purification and distribution analysis. Biophys. J. 2007, 92, 2184–2198. [Google Scholar] [CrossRef] [Green Version]
- Flier, B.M.I.; Baier, M.; Huber, J.; Mullen, K.; Mecking, S.; Zumbusch, A.; Woll, D. Single molecule fluorescence microscopy investigations on heterogeneity of translational diffusion in thin polymer films. Phys. Chem. Chem. Phys. 2011, 13, 1770–1775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akin, E.J.; Sole, L.; Johnson, B.; Beheiry, M.E.; Masson, J.B.; Krapf, D.; Tamkun, M.M. Single-molecule imaging of nav1.6 on the surface of hippocampal neurons reveals somatic nanoclusters. Biophys. J. 2016, 111, 1235–1247. [Google Scholar] [CrossRef]
- Singh, A.P.; Galland, R.; Finch-Edmondson, M.L.; Grenci, G.; Sibarita, J.B.; Studer, V.; Viasnoff, V.; Saunders, T.E. 3d protein dynamics in the cell nucleus. Biophys. J. 2017, 112, 133–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Speckner, K.; Stadler, L.; Weiss, M. Anomalous dynamics of the endoplasmic reticulum network. Phys. Rev. E 2018, 98, 012406. [Google Scholar] [CrossRef]
- Schneider, F.; Waithe, D.; Lagerholm, B.C.; Shrestha, D.; Sezgin, E.; Eggeling, C.; Fritzsche, M. Statistical analysis of scanning fluorescence correlation spectroscopy data differentiates free from hindered diffusion. ACS Nano 2018, 12, 8540–8546. [Google Scholar] [CrossRef] [Green Version]
- Porter, C.E.; Thomas, R.G. Fluctuations of nuclear reaction widths. Phys. Rev. 1956, 104, 483–491. [Google Scholar] [CrossRef]
- Sadegh, S.; Barkai, E.; Krapf, D. 1/fnoise for intermittent quantum dots exhibits non-stationarity and critical exponents. New J. Phys. 2014, 16, 113054. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. B 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Wang, B.; Kuo, J.; Bae, S.C.; Granick, S. When brownian diffusion is not gaussian. Nat. Mat. 2012, 11, 481–485. [Google Scholar] [CrossRef]
- Hapca, S.; Crawford, J.W.; Young, I.M. Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level. J. R. Soc. Interface 2009, 6, 111–122. [Google Scholar] [CrossRef] [Green Version]
- Chubynsky, M.V.; Slater, G.W. Diffusing diffusivity: A model for anomalous, yet brownian, diffusion. Phys. Rev. Lett. 2014, 113, 098302. [Google Scholar] [CrossRef] [Green Version]
- Chechkin, A.V.; Seno, F.; Metzler, R.; Sokolov, I.M. Brownian yet non-gaussian diffusion: From superstatistics to subordination of diffusing diffusivities. Phys. Rev. X 2017, 7, 021002. [Google Scholar] [CrossRef] [Green Version]
- Goychuk, I. Viscoelastic subdiffusion in a random gaussian environment. Phys. Chem. Chem. Phys. 2018, 20, 24140–24155. [Google Scholar] [CrossRef] [Green Version]
- Goychuk, I.; Pöschel, T. Finite-range viscoelastic subdiffusion in disordered systems with inclusion of inertial effects. New J. Phys. 2020, 22, 113018. [Google Scholar] [CrossRef]
- Weber, S.C.; Thompson, M.A.; Moerner, W.E.; Spakowitz, A.J.; Theriot, J.A. Analytical tools to distinguish the effects of localization error, confinement, and medium elasticity on the velocity autocorrelation function. Biophys. J. 2012, 102, 2443–2450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Backlund, M.P.; Joyner, R.; Moerner, W.E. Chromosomal locus tracking with proper accounting of static and dynamic errors. Phys. Rev. E 2015, 91, 062716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benelli, R.; Weiss, M. From sub- to superdiffusion: Fractional brownian motion of membraneless organelles in early c. elegans embryos. New J. Phys. 2021, 23, 063072. [Google Scholar] [CrossRef]
- Krapf, D.; Marinari, E.; Metzler, R.; Oshanin, G.; Xu, X.; Squarcini, A. Power spectral density of a single brownian trajectory: What one can and cannot learn from it. New J. Phys. 2018, 20, 023029. [Google Scholar] [CrossRef]
- Krapf, D.; Lukat, N.; Marinari, E.; Metzler, R.; Oshanin, G.; Selhuber-Unkel, C.; Squarcini, A.; Stadler, L.; Weiss, M.; Xu, X. Spectral content of a single non-brownian trajectory. Phys. Rev. X 2019, 9, 011019. [Google Scholar] [CrossRef] [Green Version]
- Etoc, F.; Balloul, E.; Vicario, C.; Normanno, D.; Lisse, D.; Sittner, A.; Piehler, J.; Dahan, M.; Coppey, M. Non-specific interactions govern cytosolic diffusion of nanosized objects in mammalian cells. Nat. Mater. 2018, 17, 740–746. [Google Scholar] [CrossRef] [Green Version]
- Hartich, D.; Godec, A. Thermodynamic uncertainty relation bounds the extent of anomalous diffusion. Phys. Rev. Lett. 2021, in press. [Google Scholar]
- Berry, H. Monte carlo simulations of enzyme reactions in two dimensions: Fractal kinetics and spatial segregation. Biophys. J. 2002, 83, 1891–1901. [Google Scholar] [CrossRef] [Green Version]
- Hellmann, M.; Heermann, D.W.; Weiss, M. Enhancing phosphorylation cascades by anomalous diffusion. EPL 2012, 97, 58004. [Google Scholar] [CrossRef]
- Stiehl, O.; Weidner-Hertrampf, K.; Weiss, M. Kinetics of conformational fluctuations in dna hairpin-loops in crowded fluids. New J. Phys. 2013, 15, 113010. [Google Scholar] [CrossRef]

| glyc. | [Pas] | D [] | [] | M | |
|---|---|---|---|---|---|
| 70% | 0.016 | 0.67 | 1.00 | 0.56 | 929 |
| 0.99 | 0.45 | 67 | |||
| 75% | 0.023 | 0.46 | 1.01 | 0.42 | 1513 |
| 1.03 | 0.35 | 185 | |||
| 80% | 0.035 | 0.30 | 1.01 | 0.28 | 2158 |
| 1.03 | 0.24 | 250 | |||
| 85% | 0.055 | 0.19 | 1.01 | 0.20 | 4426 |
| 1.02 | 0.18 | 749 | |||
| 90% | 0.096 | 0.11 | 1.00 | 0.13 | 4668 |
| 1.02 | 0.12 | 980 |
| cond. | M | ||
|---|---|---|---|
| untreated | 0.89 | 0.39 | 3085 |
| 0.88 | 0.27 | 582 | |
| +taxol | 0.83 | 0.33 | 2548 |
| 0.81 | 0.25 | 606 | |
| +nocodazol | 0.89 | 0.37 | 1126 |
| 0.81 | 0.17 | 130 | |
| +ATPS +GTPS | 0.85 | 0.31 | 915 |
| 0.81 | 0.10 | 189 | |
| +ATPS +GTPS +noc. | 0.88 | 0.35 | 2646 |
| 0.83 | 0.23 | 471 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speckner, K.; Weiss, M. Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts. Entropy 2021, 23, 892. https://doi.org/10.3390/e23070892
Speckner K, Weiss M. Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts. Entropy. 2021; 23(7):892. https://doi.org/10.3390/e23070892
Chicago/Turabian StyleSpeckner, Konstantin, and Matthias Weiss. 2021. "Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts" Entropy 23, no. 7: 892. https://doi.org/10.3390/e23070892
APA StyleSpeckner, K., & Weiss, M. (2021). Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts. Entropy, 23(7), 892. https://doi.org/10.3390/e23070892






