Quantum Euler Relation for Local Measurements
Abstract
1. Introduction
2. The Information Gain
2.1. Positive Operator-Valued Measures
2.2. Maximal Information Gain
Illustrative Example:
2.3. The Holevo Bound
Illustrative Example:
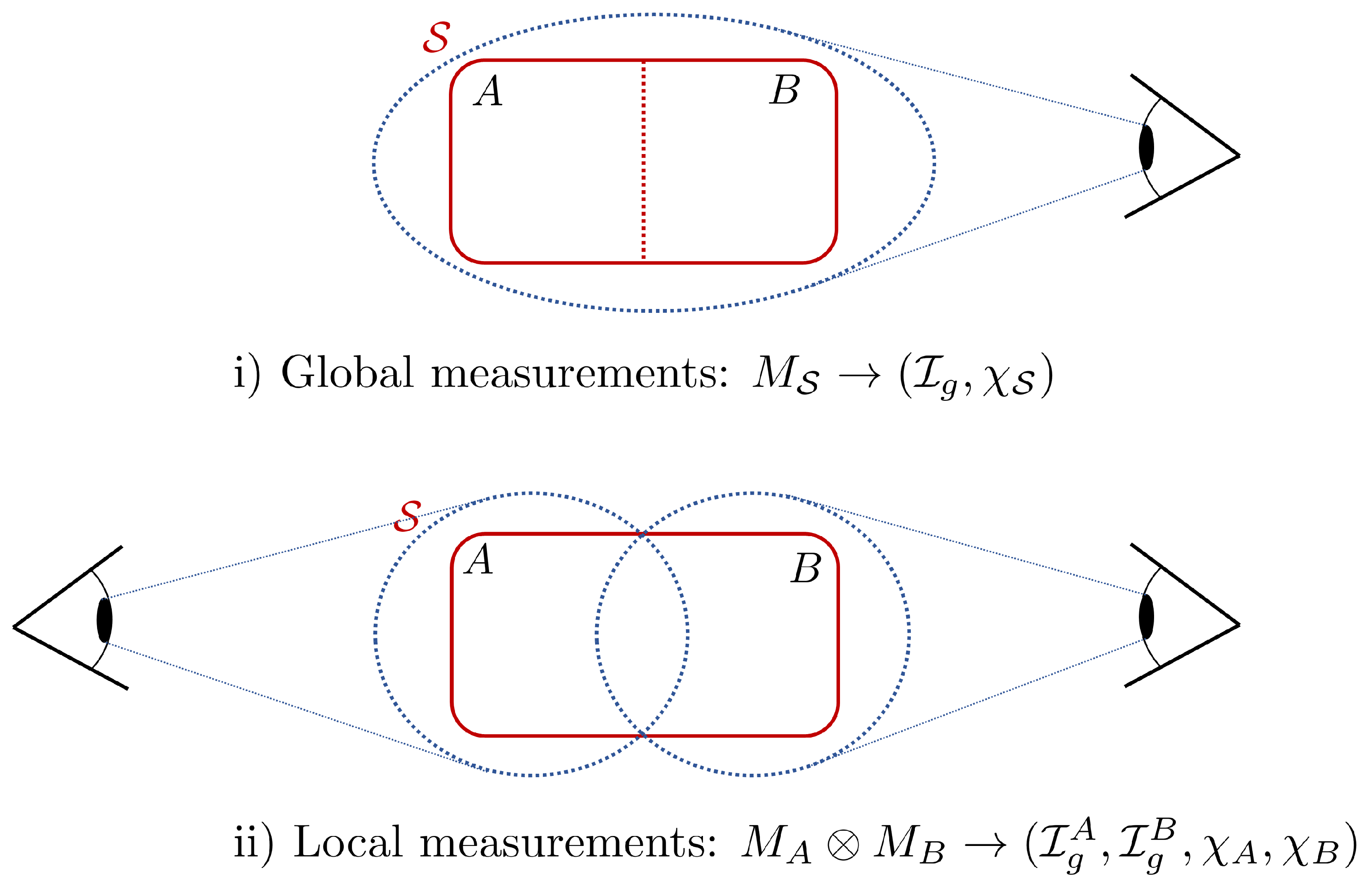
3. Projective Local Measurements
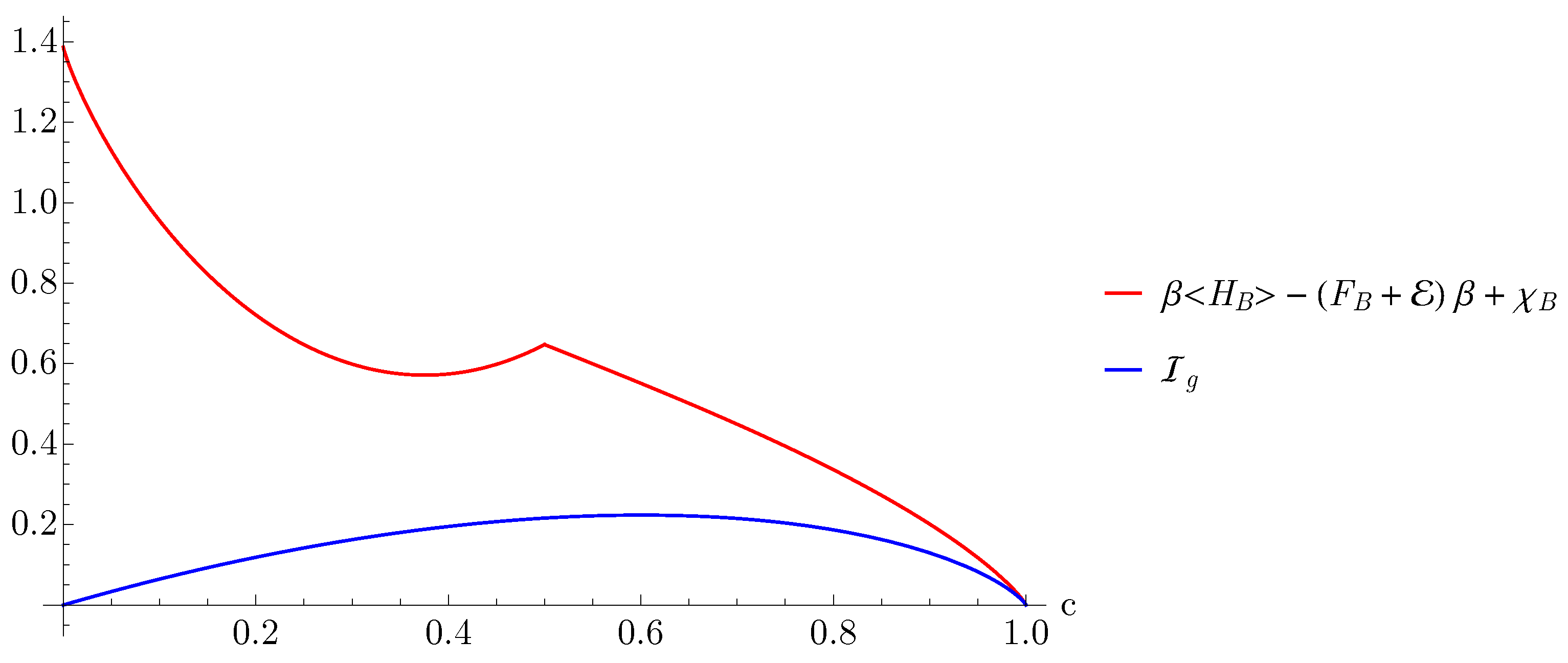
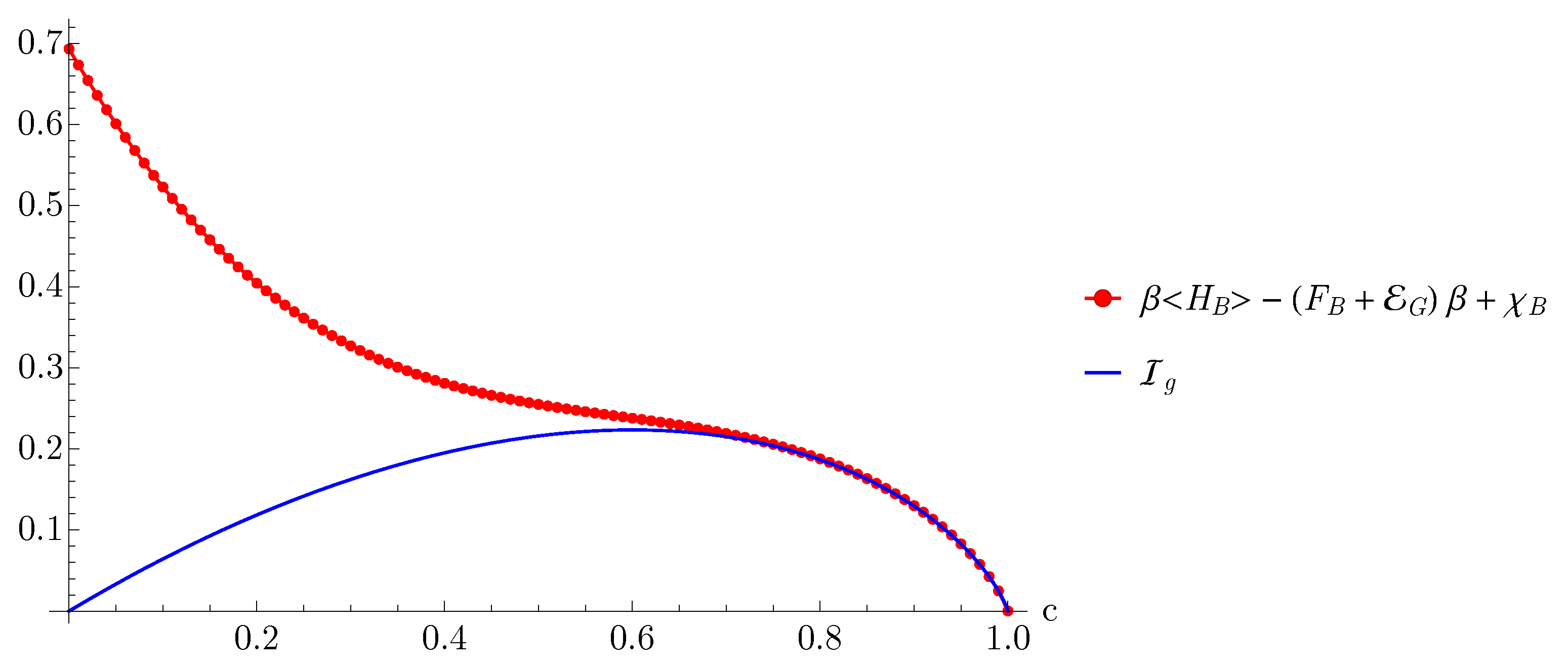
3.1. Quantum and Classical Contributions
3.2. Maximum Extractable Work
4. Collective Dissipation
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; American Association of Physics Teachers: College Park, MD, USA, 1998. [Google Scholar]
- Huang, K. Introduction to Statistical Physics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Carnot, S. Réflexions Sur la Puissance Motrice du Feu; Number 26; Vrin: Paris, France, 1978. [Google Scholar]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation—A review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Deffner, S.; Campbell, S. Quantum Thermodynamics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019; pp. 2053–2571. [Google Scholar] [CrossRef]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Generalized Jarzynski Equality under Nonequilibrium Feedback Control. Phys. Rev. Lett. 2010, 104, 090602. [Google Scholar] [CrossRef]
- Deutsch, I.H. Harnessing the Power of the Second Quantum Revolution. PRX Quantum 2020, 1, 020101. [Google Scholar] [CrossRef]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1655–1674. [Google Scholar] [CrossRef]
- Francica, G.; Binder, F.C.; Guarnieri, G.; Mitchison, M.T.; Goold, J.; Plastina, F. Quantum Coherence and Ergotropy. Phys. Rev. Lett. 2020, 125, 180603. [Google Scholar] [CrossRef] [PubMed]
- Korzekwa, K.; Lostaglio, M.; Oppenheim, J.; Jennings, D. The extraction of work from quantum coherence. New J. Phys. 2016, 18, 023045. [Google Scholar] [CrossRef]
- Çakmak, B. Ergotropy from coherences in an open quantum system. Phys. Rev. E 2020, 102, 042111. [Google Scholar] [CrossRef]
- Guarnieri, G.; Morrone, D.; Çakmak, B.; Plastina, F.; Campbell, S. Non-equilibrium steady-states of memoryless quantum collision models. Phys. Lett. A 2020, 126576. [Google Scholar] [CrossRef]
- Funo, K.; Watanabe, Y.; Ueda, M. Thermodynamic work gain from entanglement. Phys. Rev. A 2013, 88, 052319. [Google Scholar] [CrossRef]
- Francica, G.; Goold, J.; Plastina, F.; Paternostro, M. Daemonic ergotropy: Enhanced work extraction from quantum correlations. NPJ Quantum Inf. 2017, 3, 12. [Google Scholar] [CrossRef]
- Bernards, F.; Kleinmann, M.; Gühne, O.; Paternostro, M. Daemonic Ergotropy: Generalised Measurements and Multipartite Settings. Entropy 2019, 21, 771. [Google Scholar] [CrossRef] [PubMed]
- Manzano, G.; Plastina, F.; Zambrini, R. Optimal Work Extraction and Thermodynamics of Quantum Measurements and Correlations. Phys. Rev. Lett. 2018, 121, 120602. [Google Scholar] [CrossRef] [PubMed]
- Perarnau-Llobet, M.; Hovhannisyan, K.V.; Huber, M.; Skrzypczyk, P.; Brunner, N.; Acín, A. Extractable Work from Correlations. Phys. Rev. X 2015, 5, 041011. [Google Scholar] [CrossRef]
- Fusco, L.; Paternostro, M.; De Chiara, G. Work extraction and energy storage in the Dicke model. Phys. Rev. E 2016, 94, 052122. [Google Scholar] [CrossRef]
- Sapienza, F.; Cerisola, F.; Roncaglia, A.J. Correlations as a resource in quantum thermodynamics. Nat. Commun. 2019, 10, 1–7. [Google Scholar] [CrossRef]
- Oppenheim, J.; Horodecki, M.; Horodecki, P.; Horodecki, R. Thermodynamical Approach to Quantifying Quantum Correlations. Phys. Rev. Lett. 2002, 89, 180402. [Google Scholar] [CrossRef] [PubMed]
- Jevtic, S.; Jennings, D.; Rudolph, T. Maximally and Minimally Correlated States Attainable within a Closed Evolving System. Phys. Rev. Lett. 2012, 108, 110403. [Google Scholar] [CrossRef]
- Touil, A.; Çakmak, B.; Deffner, S. Second law of thermodynamics for quantum correlations. arXiv 2021, arXiv:2102.13606. [Google Scholar]
- Sagawa, T.; Ueda, M. Second Law of Thermodynamics with Discrete Quantum Feedback Control. Phys. Rev. Lett. 2008, 100, 080403. [Google Scholar] [CrossRef]
- Groenewold, H.J. A problem of information gain by quantal measurements. Int. J. Theo. Phys. 1971, 4, 327. [Google Scholar] [CrossRef]
- Holevo, A.S. Bounds for the quantity of information transmitted by a quantum communication channel. Probl. Peredachi Informatsii 1973, 9, 3–11. [Google Scholar]
- Nielsen, M.A.; Chuang, I. Quantum computation and quantum information. Am. J. Phys. 2002, 70. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 2013; Volume 38. [Google Scholar]
- Thingna, J.; Talkner, P. Quantum measurements of sums. Phys. Rev. A 2020, 102, 012213. [Google Scholar] [CrossRef]
- Luo, S. Information conservation and entropy change in quantum measurements. Phys. Rev. A 2010, 82, 052103. [Google Scholar] [CrossRef]
- Buscemi, F.; Hayashi, M.; Horodecki, M. Global Information Balance in Quantum Measurements. Phys. Rev. Lett. 2008, 100, 210504. [Google Scholar] [CrossRef]
- Ozawa, M. On information gain by quantum measurements of continuous observables. J. Math. Phys. 1986, 27, 759–763. [Google Scholar] [CrossRef]
- Lindblad, G. An entropy inequality for quantum measurements. Commun. Math. Phys. 1972, 28, 245–249. [Google Scholar] [CrossRef]
- Lindblad, G. Entropy, information and quantum measurements. Commun. Math. Phys. 1973, 33, 305–322. [Google Scholar] [CrossRef]
- Xi, Z. Information gain and information leak in quantum measurements. Phys. Rev. A 2016, 93, 052308. [Google Scholar] [CrossRef]
- Naghiloo, M.; Alonso, J.J.; Romito, A.; Lutz, E.; Murch, K.W. Information Gain and Loss for a Quantum Maxwell’s Demon. Phys. Rev. Lett. 2018, 121, 030604. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Jacobs, K. Information-tradeoff relations for finite-strength quantum measurements. Phys. Rev. A 2001, 63, 062305. [Google Scholar] [CrossRef]
- Lindblad, G. Completely positive maps and entropy inequalities. Commun. Math. Phys. 1975, 40, 147–151. [Google Scholar] [CrossRef]
- Vedral, V.; Rippin, M.; Plenio, M. Quantum correlations, local interactions and error correction. J. Mod. Opt. 1997, 44, 2185–2205. [Google Scholar] [CrossRef][Green Version]
- Deffner, S.; Lutz, E. Nonequilibrium Entropy Production for Open Quantum Systems. Phys. Rev. Lett. 2011, 107, 140404. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying Entanglement. Phys. Rev. Lett. 1997, 78, 2275–2279. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Kafri, D.; Deffner, S. Holevo’s bound from a general quantum fluctuation theorem. Phys. Rev. A 2012, 86, 044302. [Google Scholar] [CrossRef]
- Koashi, M.; Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 2004, 69, 022309. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar] [CrossRef] [PubMed]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34, 6899. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Maximal work extraction from finite quantum systems. EPL 2004, 67, 565. [Google Scholar] [CrossRef]
- Sone, A.; Deffner, S. Quantum and classical ergotropy from relative entropies. arXiv 2021, arXiv:2103.10850. [Google Scholar]
- Niedenzu, W.; Huber, M.; Boukobza, E. Concepts of work in autonomous quantum heat engines. Quantum 2019, 3, 195. [Google Scholar] [CrossRef]
- Quesada, N.; Al-Qasimi, A.; James, D.F. Quantum properties and dynamics of X states. J. Mod. Opt. 2012, 59, 1322–1329. [Google Scholar] [CrossRef]
- Cai, J.M.; Zhou, Z.W.; Guo, G.C. Stability of pairwise entanglement in a decoherent environment. Phys. Rev. A 2005, 72, 022312. [Google Scholar] [CrossRef]
- Carnio, E.G.; Buchleitner, A.; Gessner, M. Generating and protecting correlated quantum states under collective dephasing. New J. Phys. 2016, 18, 073010. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Sarandy, M.S.; De Oliveira, T.R.; Amico, L. Quantum discord in the ground state of spin chains. Int. J. Mod. Phys. B 2013, 27, 1345030. [Google Scholar] [CrossRef]
- Çakmak, B.; Karpat, G.; Fanchini, F.F. Factorization and Criticality in the Anisotropic XY Chain via Correlations. Entropy 2015, 17, 790–817. [Google Scholar] [CrossRef]
- Çakmak, B.; Manatuly, A.; Müstecaplıoğlu, O.E. Thermal production, protection, and heat exchange of quantum coherences. Phys. Rev. A 2017, 96, 032117. [Google Scholar] [CrossRef]
- Latune, C.L.; Sinayskiy, I.; Petruccione, F. Energetic and entropic effects of bath-induced coherences. Phys. Rev. A 2019, 99, 052105. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Stephen, M.J. First-Order Dispersion Forces. J. Chem. Phys. 1964, 40, 669–673. [Google Scholar] [CrossRef]
- Lehmberg, R.H. Radiation from an N-Atom System. I. General Formalism. Phys. Rev. A 1970, 2, 883–888. [Google Scholar] [CrossRef]
- Damanet, F.; Martin, J. Competition between finite-size effects and dipole–dipole interactions in few-atom systems. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 225501. [Google Scholar] [CrossRef]
- Thingna, J.; Manzano, D.; Cao, J. Dynamical signatures of molecular symmetries in nonequilibrium quantum transport. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Thingna, J.; Manzano, D.; Cao, J. Magnetic field induced symmetry breaking in nonequilibrium quantum networks. New J. Phys. 2020, 22, 083026. [Google Scholar] [CrossRef]
- Deffner, S. Demonstration of entanglement assisted invariance on IBM’s quantum experience. Heliyon 2017, 3, e00444. [Google Scholar] [CrossRef]
- Berta, M.; Wehner, S.; Wilde, M.M. Entropic uncertainty and measurement reversibility. New J. Phys. 2016, 18, 073004. [Google Scholar] [CrossRef]
- Devitt, S.J. Performing quantum computing experiments in the cloud. Phys. Rev. A 2016, 94, 032329. [Google Scholar] [CrossRef]
- Rundle, R.P.; Mills, P.W.; Tilma, T.; Samson, J.H.; Everitt, M.J. Simple procedure for phase-space measurement and entanglement validation. Phys. Rev. A 2017, 96, 022117. [Google Scholar] [CrossRef]
- Solfanelli, A.; Santini, A.; Campisi, M. Experimental verification of fluctuation relations with a quantum computer. arXiv 2021, arXiv:2106.04388. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Touil, A.; Weber, K.; Deffner, S. Quantum Euler Relation for Local Measurements. Entropy 2021, 23, 889. https://doi.org/10.3390/e23070889
Touil A, Weber K, Deffner S. Quantum Euler Relation for Local Measurements. Entropy. 2021; 23(7):889. https://doi.org/10.3390/e23070889
Chicago/Turabian StyleTouil, Akram, Kevin Weber, and Sebastian Deffner. 2021. "Quantum Euler Relation for Local Measurements" Entropy 23, no. 7: 889. https://doi.org/10.3390/e23070889
APA StyleTouil, A., Weber, K., & Deffner, S. (2021). Quantum Euler Relation for Local Measurements. Entropy, 23(7), 889. https://doi.org/10.3390/e23070889






