Why Dilated Convolutional Neural Networks: A Proof of Their Optimality
Abstract
:1. Introduction
1.1. Convolutional Layers: Input and Outpu
- the input to this layer consists of the values , where , , and are integers for which , , and ; and
- the output of this layer consists of the values , where d, x, and y are integers for which , , and .
1.2. Convolutional Layer: Transformation
- first, each value depends only on the values , for which both differences and do not exceed some fixed integer L, and
- the coefficients depend only on the differences and :for some coefficients defined for all pairs for which .
1.3. Sparse Filters and Dilated Convolution
1.4. Empirical Fact That Needs Explanation
2. Analysis of The Problem
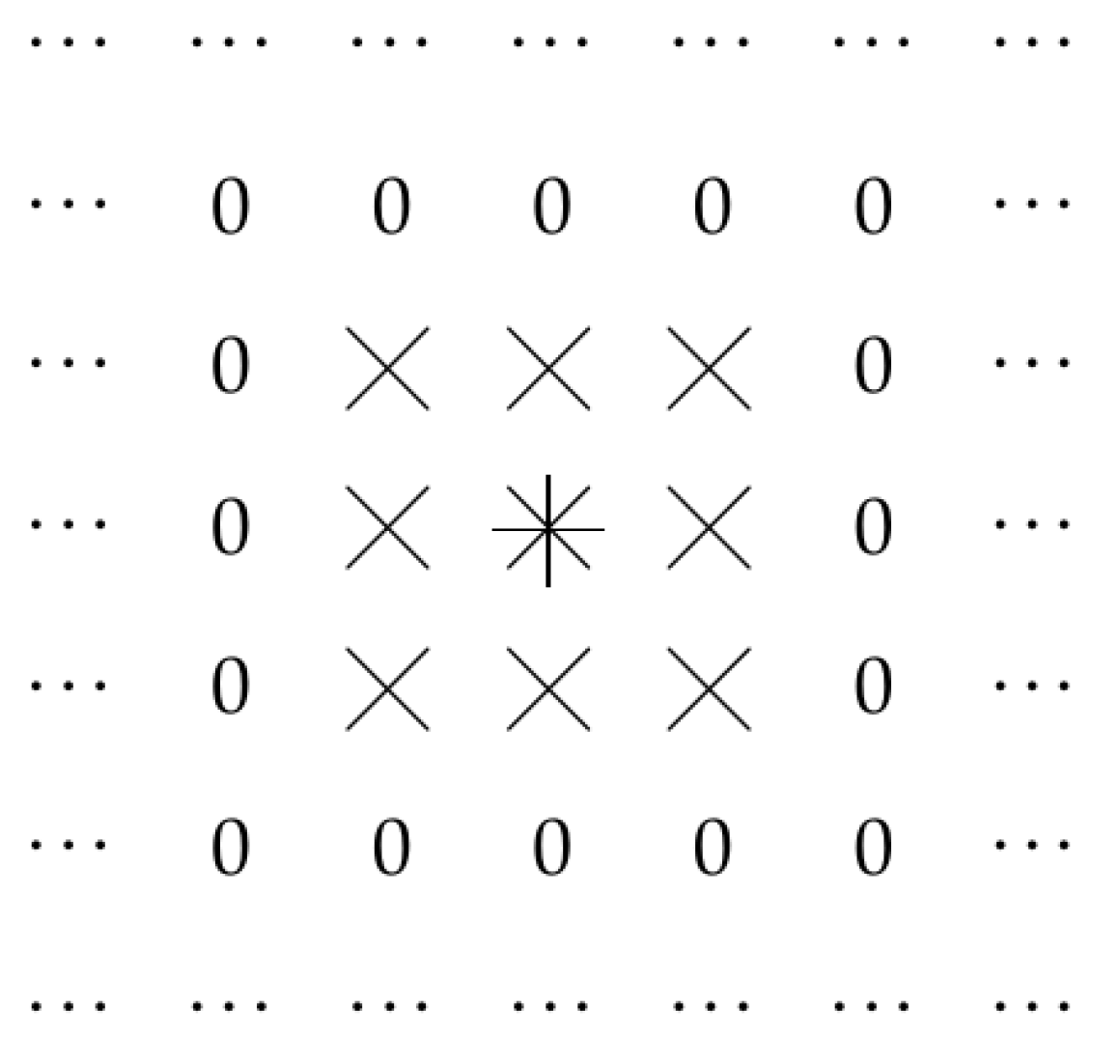
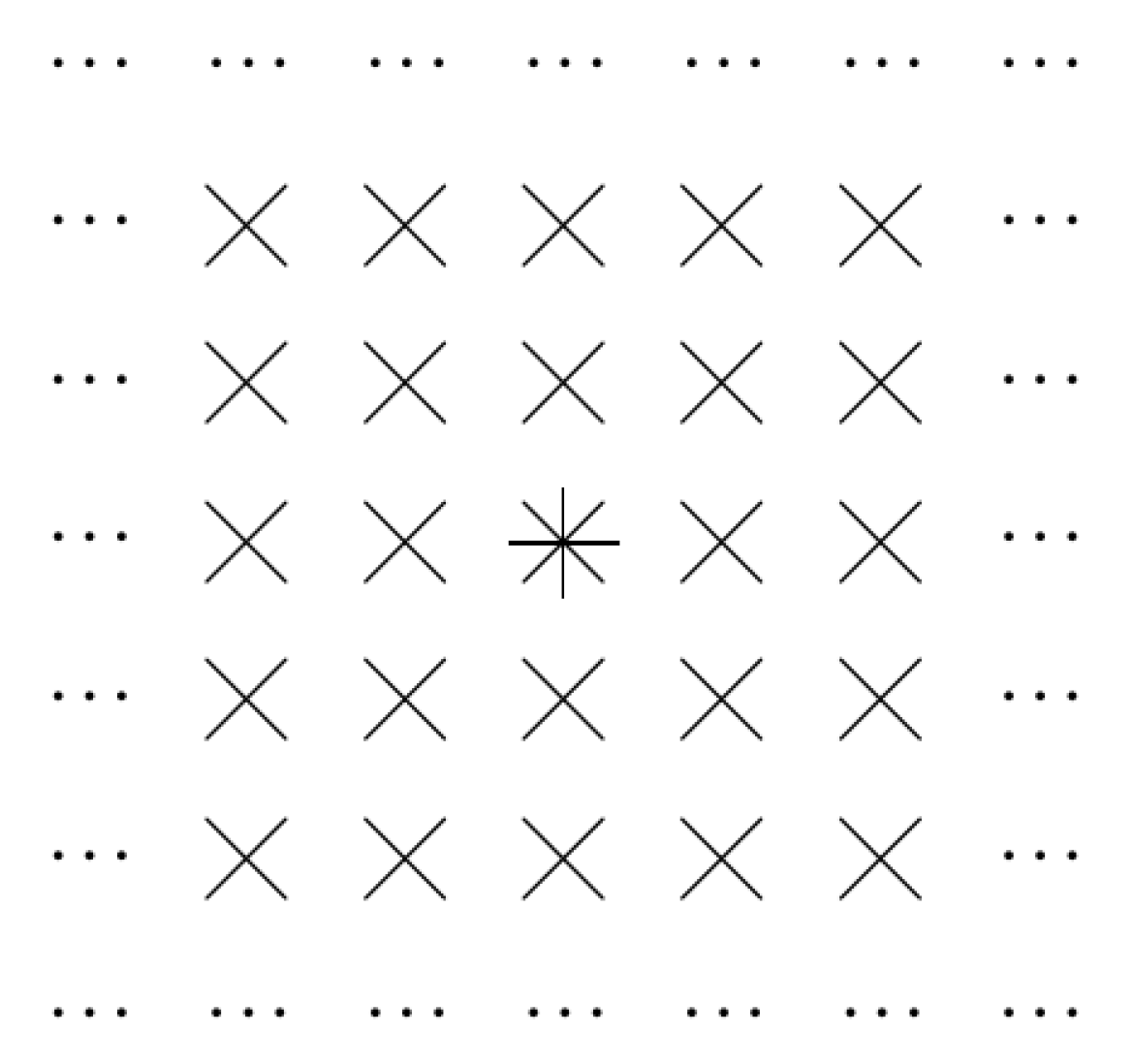
2.1. Let Us Reformulate This Situation in Geometric Terms: Case of Traditional Convolution
2.2. Case of Dilated Convolution
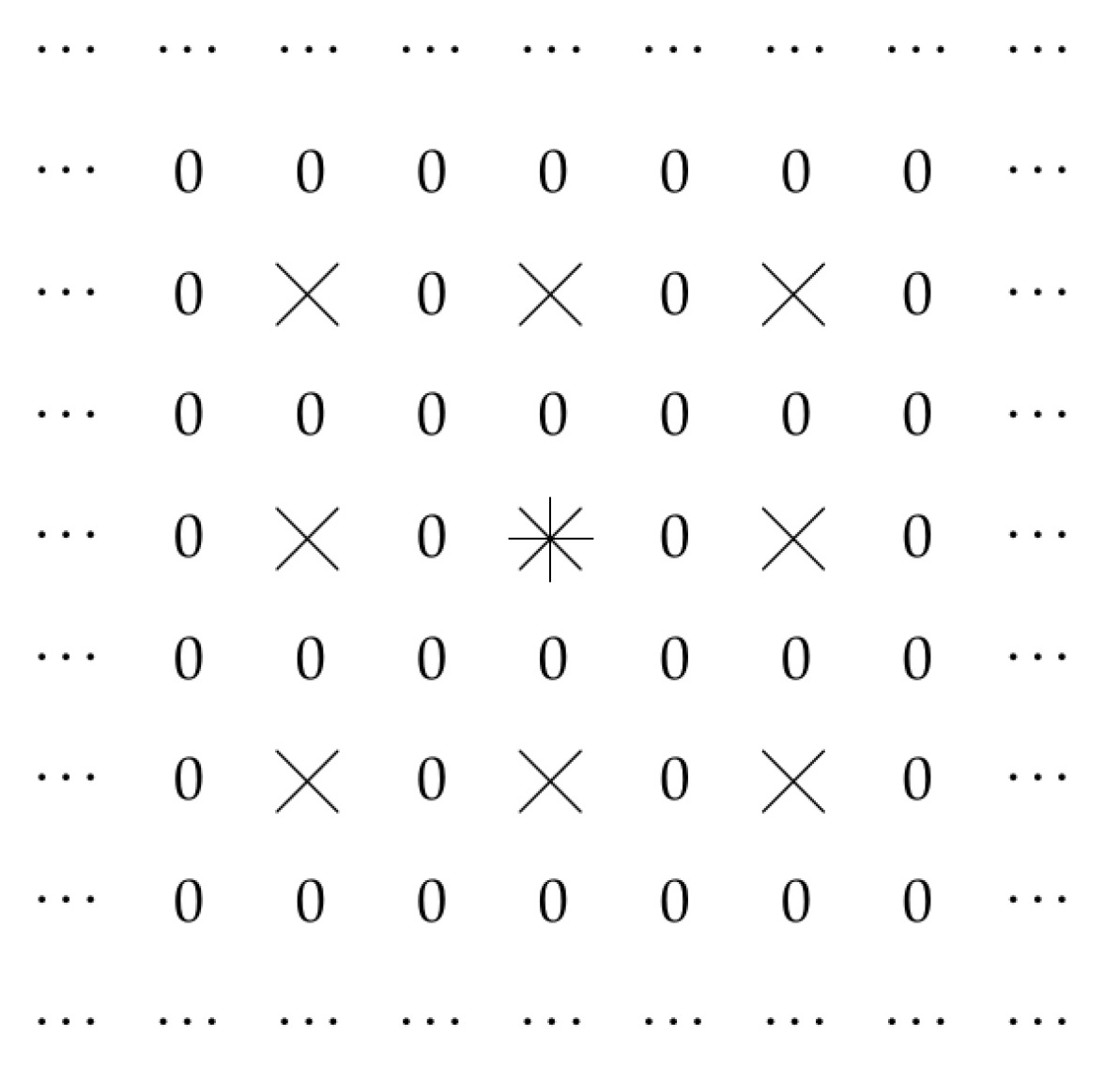
2.3. Other Cases
- for points for which y is even, we take
- and for points for which y is odd, we take
2.4. General Case
- we have a family of subsets of the “grid” ;
- the values of the layer’s output signal at a point are determined by the formulafor some values , where denotes the set from the family that contains the point .
- different sets from the family must be disjoint, and
- the union of all the sets must coincide with the whole “grid” .
2.5. We Do Not a Priori Require Shift-Invariance
2.6. Let Us Avoid the Degenerate Case
2.7. What We Plan to Do
2.8. What Does “Optimal” Mean?
- we have an objective function that assigns a numerical value to each alternative a—e.g., the average approximation error of the numerical method a for solving a system of differential equations, and
- optimal means that we select an alternative for which the value of this objective function is the smallest possible (or, for some objective functions, the largest possible).
- either we have ,
- or we have and .
- for some of these pairs, we have ,
- for some of these pairs, we have , and
- for some others pairs, we conclude that alternatives a and b are, from our viewpoint, of equal value; we will denote this by .
2.9. Invariance
- if we shift each image I from the set by the same shift , i.e., replace each image by a shifted image for which ,
- then, we should get, in effect, the exact same set of images:
- values corresponding to several points
- into values corresponding to a single new point .
- the relative quality of two families does not change if we shift all the layer’s inputs;
- however, shifting all the layer’s inputs is equivalent to shifting all the sets from the family .
3. Definitions and the Main Result
- all sets from this family are disjoint, and
- at least one set from this family has more than one element.
- first, we consider points ;
- second, we consider sets of points ; we call them simply sets;
- third, we consider sets of sets of points ; we call them families;
- finally, we consider the set of all possible families ; we call this a class.
- if and , then ;
- if and , then ;
- if and , then ;
- if and , then ;
- we have for all ; and
- if , then we cannot have .
- the family of all the sets corresponding to all possible pairs of integers for which ;
- the family of all the setscorresponding to all possible pairs of integers for which .
- This proposition takes care of all invariant (and final) optimality criteria. Thus, it should work for all usual criteria based on misclassification rate, time of calculation, used memory, or any others used in neural networks: indeed, if one method is better than another for images in general, it should remain to be better if we simply shift all the images or turn all the images upside down. Images can come as they are, they can come upside down, they can come shifted, etc. If, for some averaging criterion, one method works better for all possible images, but another method works better for all upside-down versions of these images—which is, in effect, the same class of possible images—then, from the common sense viewpoint, this would mean that something is not right with this criterion.
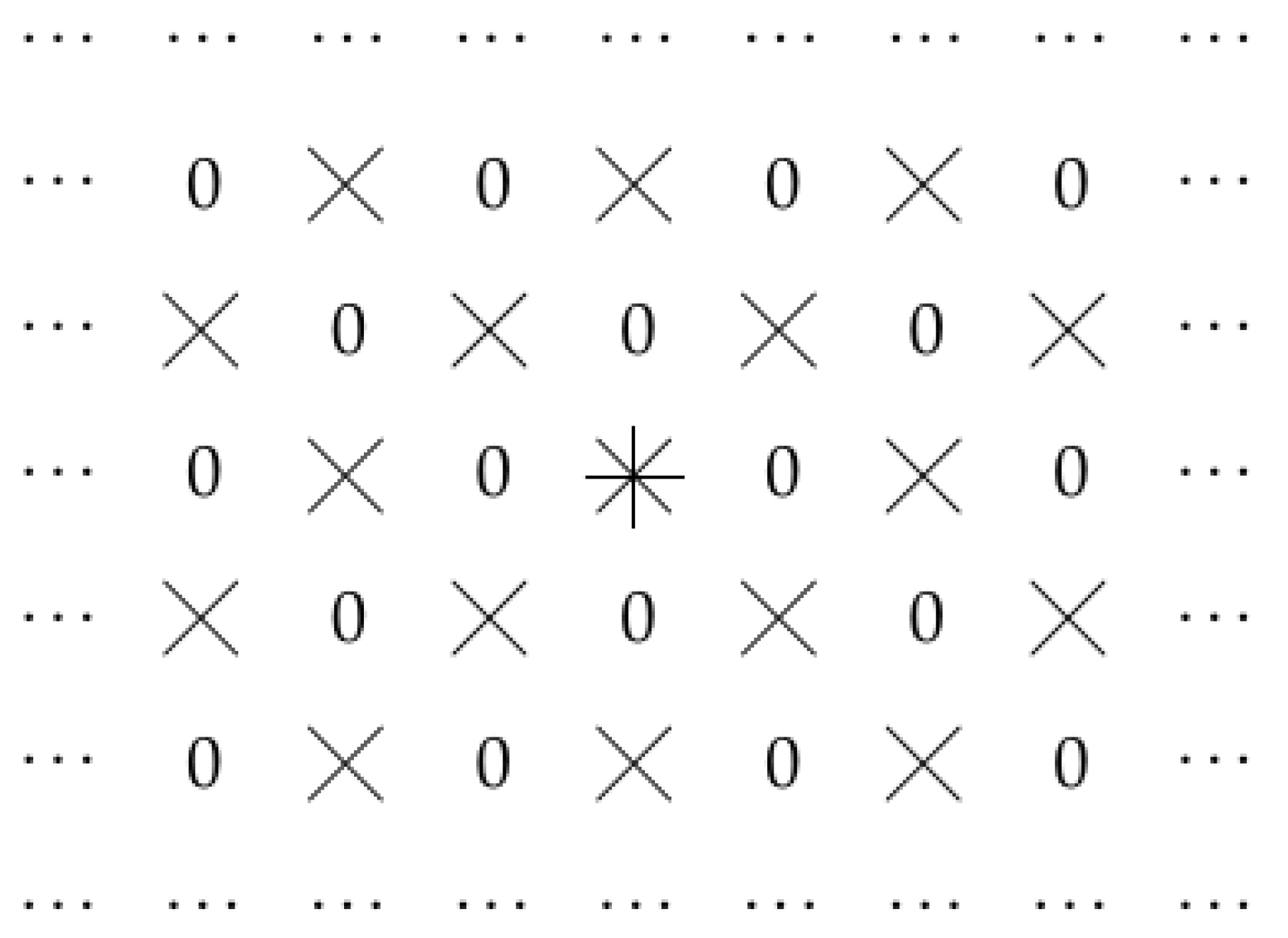
- The first possibly optimal case corresponds to dilated convolution. In the second possibly optimal case, the optimal family contains similar but somewhat different sets; an example of such a set is given in Figure 7.Thus, this result explains the effectiveness of dilated convolution—and also provides us with a new alternative worth trying.
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Leaning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Li, Y.; Zhang, X.; Chen, D. CSRNet: Dilated convolutional neural networks for understanding the highly congested scenes. In Proceedings of the 2018 Conference on Computer Vision and Pattern Recognition CVPR’2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1091–1100. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. In Proceedings of the 4th International Conference on Learning Representations ICLR’2016, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Zhang, X.; Zou, Y.; Shi, W. Dilated convolution neural network with LeakyReLU for environmental sound classification. In Proceedings of the 2017 22nd International Conference on Digital Signal Processing DSP’2017, London, UK, 23–25 August 2017. [Google Scholar]
- Nguyen, H.T.; Kreinovich, V. Applications of Continuous Mathematics to Computer Science; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Kreinovich, V.; Kosheleva, O. Optimization under uncertainty explains empirical success of deep learning heuristics. In Black Box Optimization, Machine Learning and No-Free Lunch Theorems; Pardalos, P., Rasskazova, V., Vrahatis, M.N., Eds.; Springer: Cham, Switzerland, 2021; pp. 195–220. [Google Scholar]


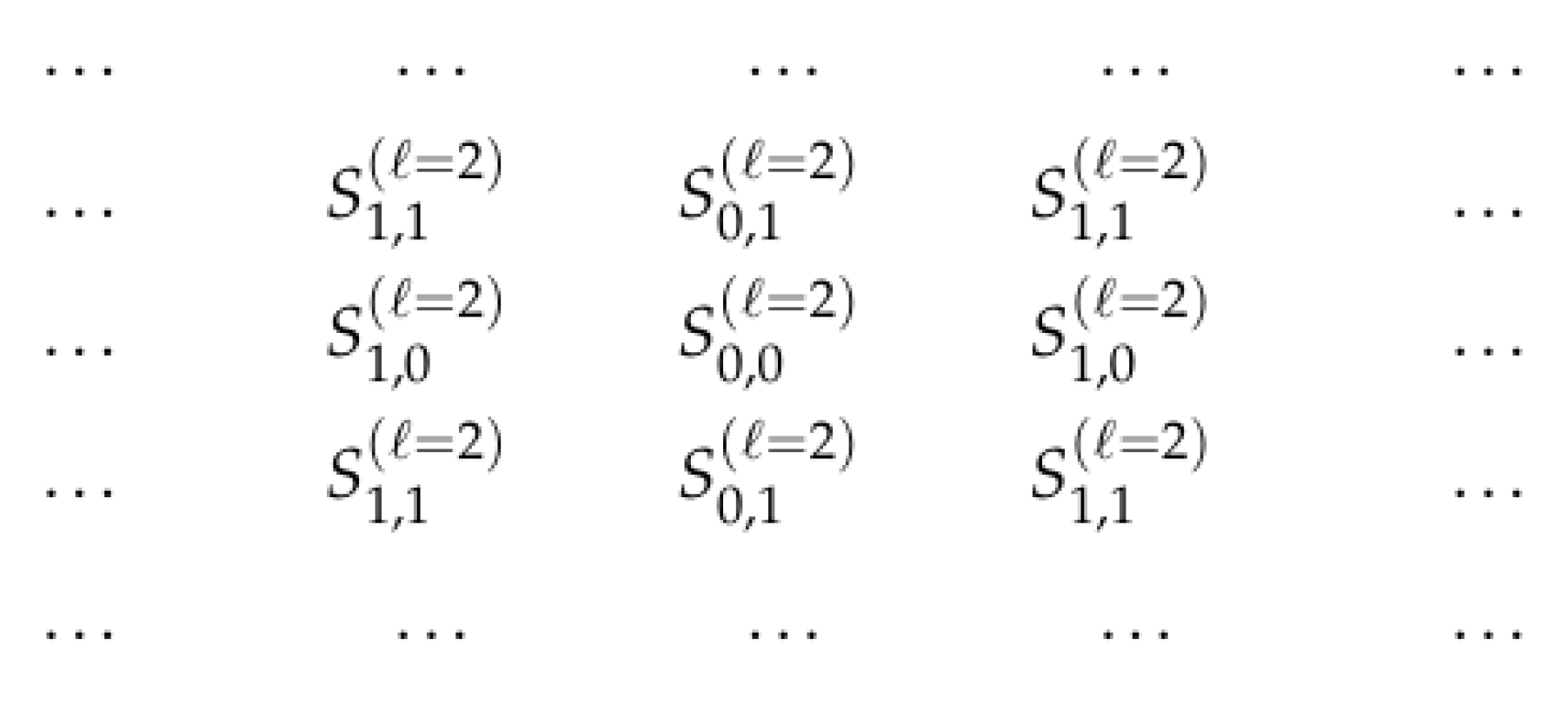
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras, J.; Ceberio, M.; Kreinovich, V. Why Dilated Convolutional Neural Networks: A Proof of Their Optimality. Entropy 2021, 23, 767. https://doi.org/10.3390/e23060767
Contreras J, Ceberio M, Kreinovich V. Why Dilated Convolutional Neural Networks: A Proof of Their Optimality. Entropy. 2021; 23(6):767. https://doi.org/10.3390/e23060767
Chicago/Turabian StyleContreras, Jonatan, Martine Ceberio, and Vladik Kreinovich. 2021. "Why Dilated Convolutional Neural Networks: A Proof of Their Optimality" Entropy 23, no. 6: 767. https://doi.org/10.3390/e23060767
APA StyleContreras, J., Ceberio, M., & Kreinovich, V. (2021). Why Dilated Convolutional Neural Networks: A Proof of Their Optimality. Entropy, 23(6), 767. https://doi.org/10.3390/e23060767





