Assessment of Classification Models and Relevant Features on Nonalcoholic Steatohepatitis Using Random Forest
Abstract
1. Introduction
Related Work
2. Methods
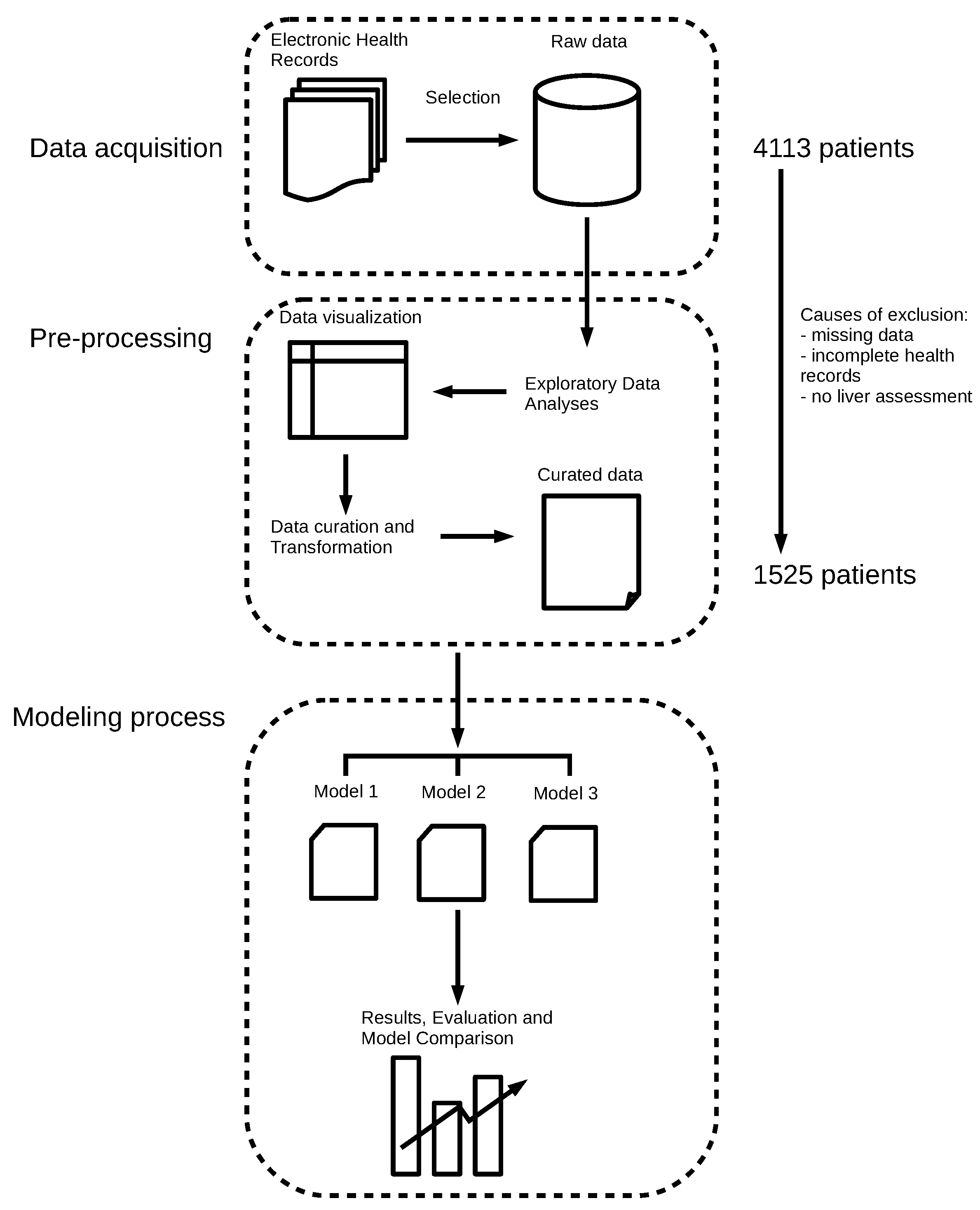
2.1. Data Collection, Exploratory Data Analysis, and Preprocessing
2.2. Class Imbalance
2.3. Data Splitting and Metrics for Performance
2.4. Modeling with the Random Forest Algorithm and Searching for Tuning Parameters
2.5. Interpretability of Random Forest Models
2.5.1. Importance of Features
2.5.2. Partial Dependence Plots
2.5.3. Contribution of Each Feature to the Predictions
2.6. Experimental Setup
3. Results
3.1. Descriptive Analyses
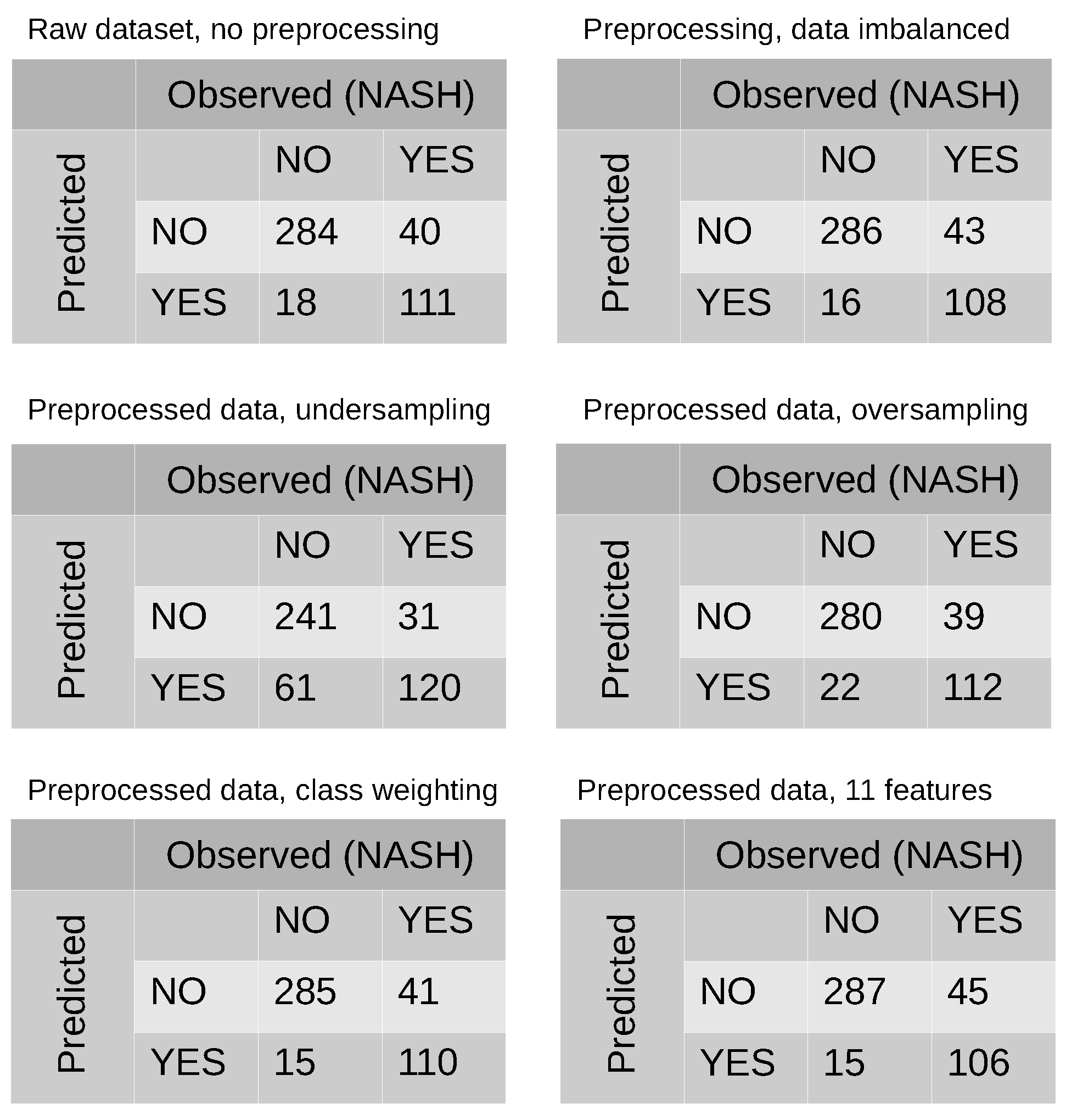
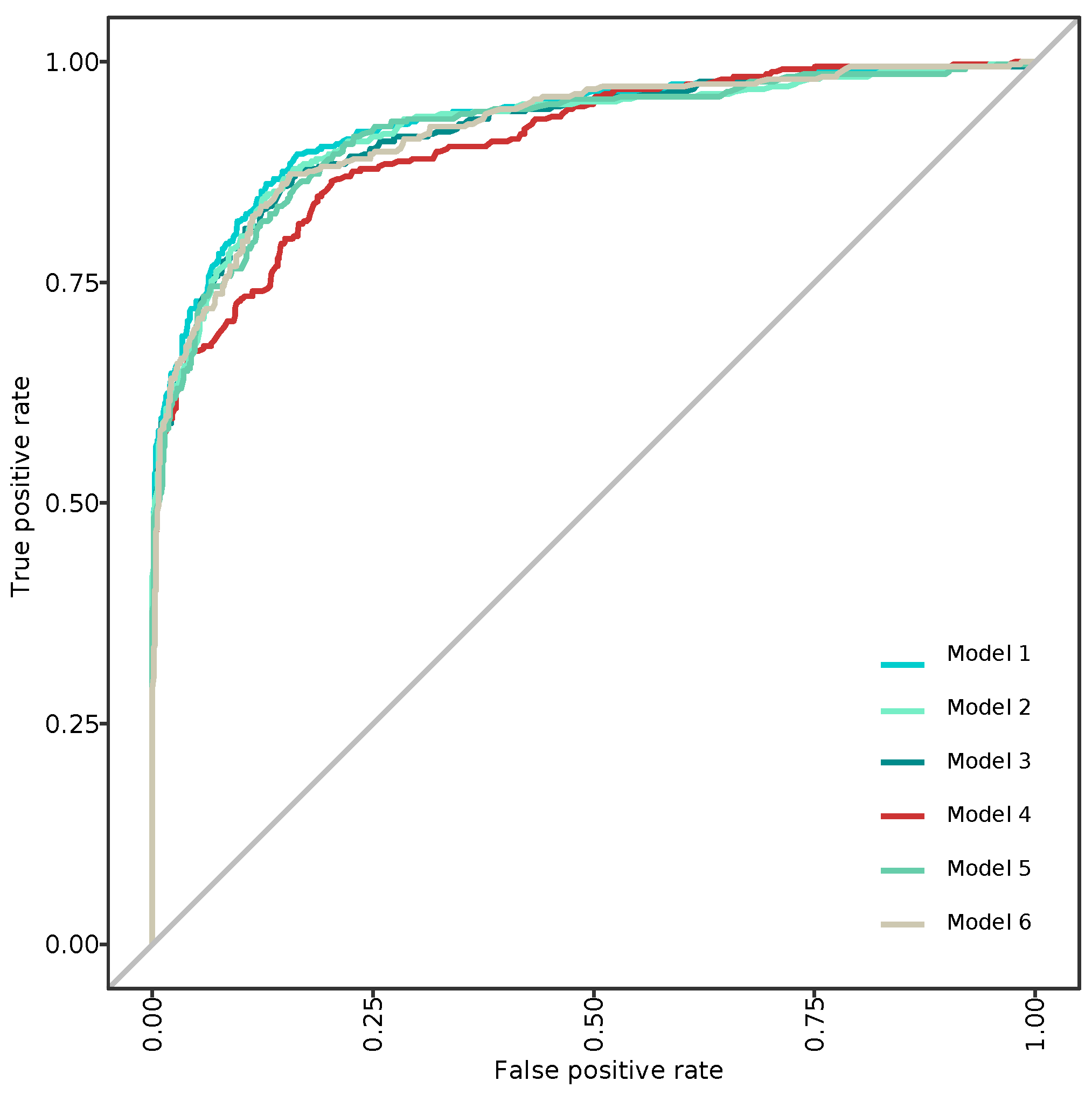
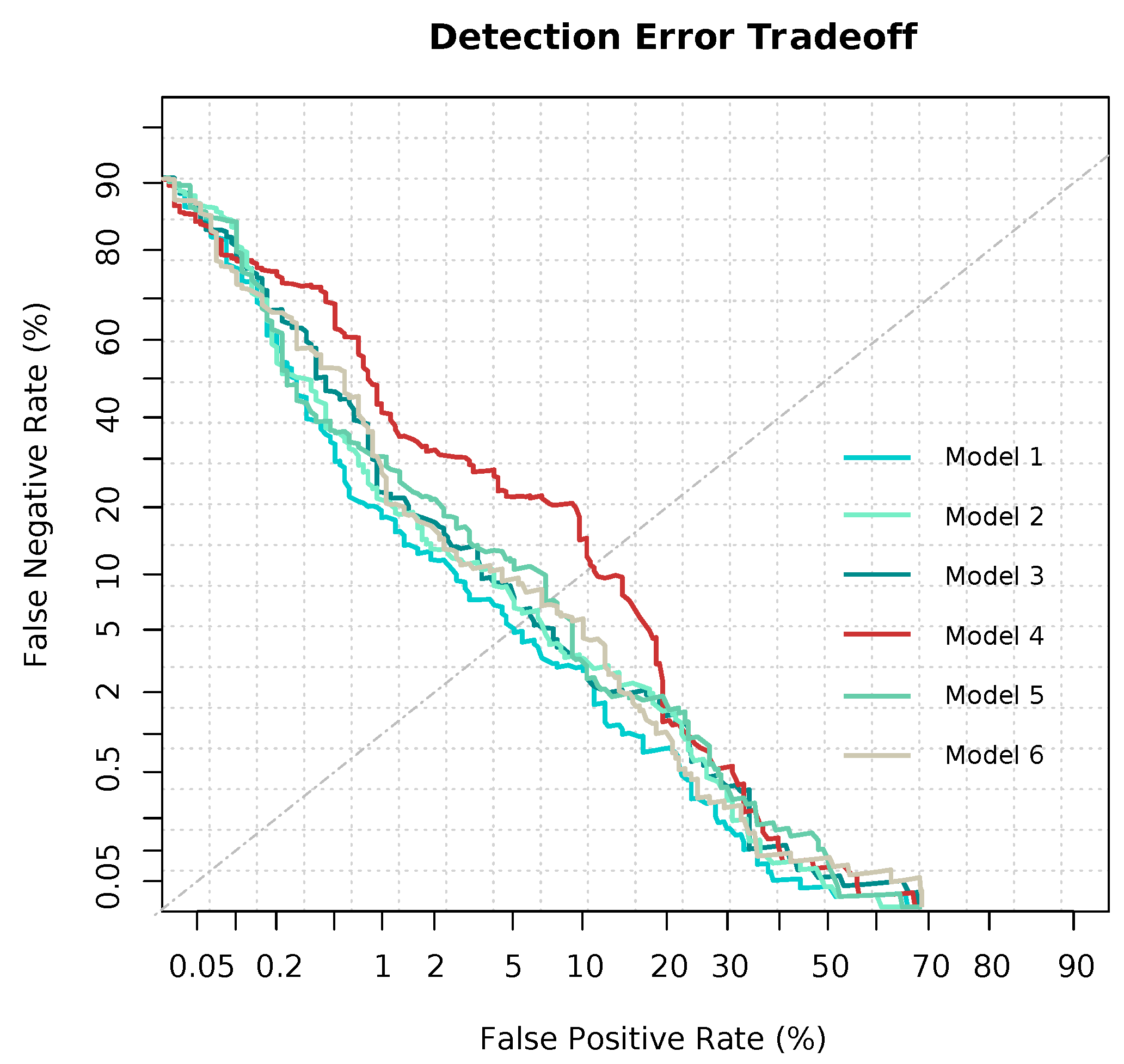
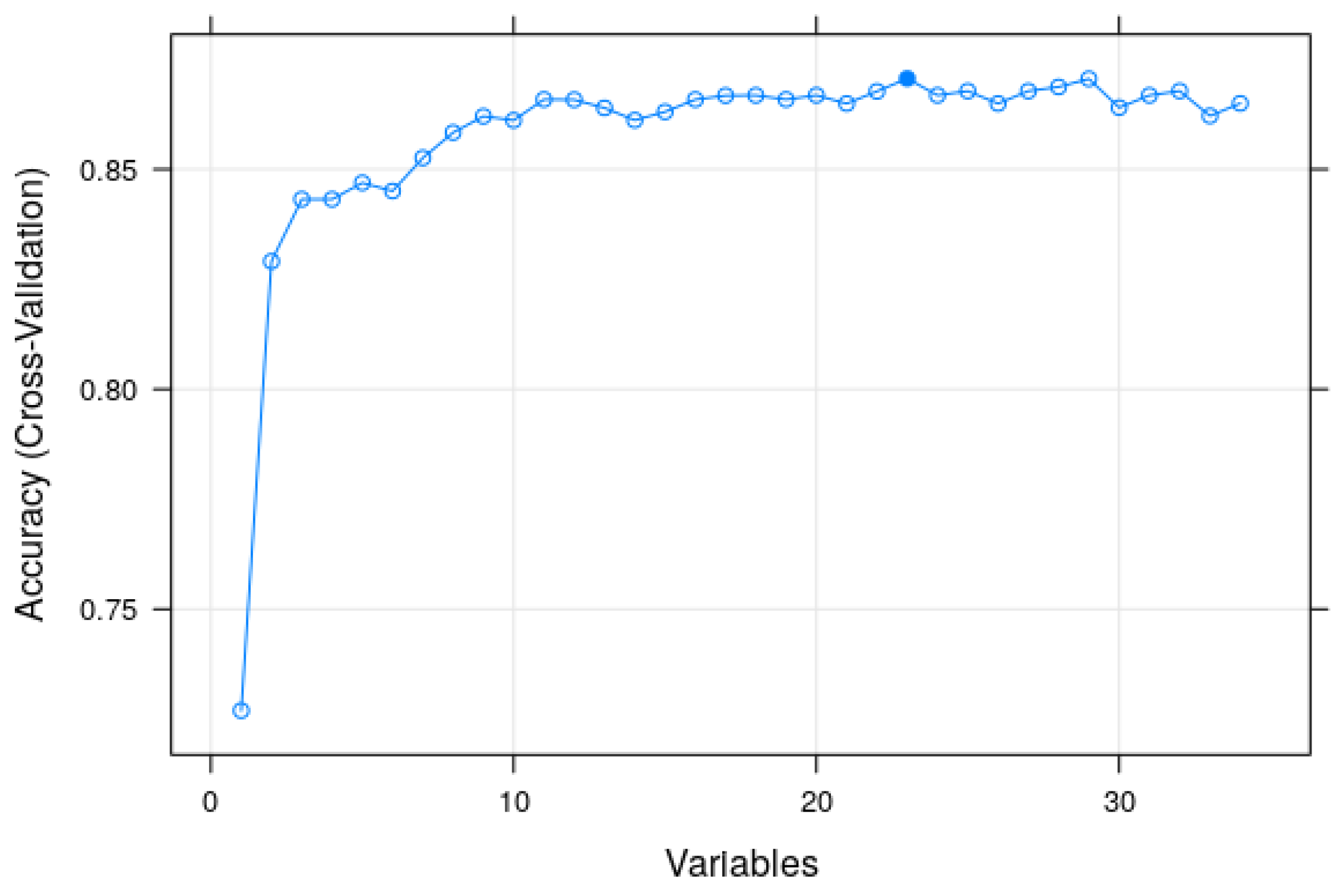
3.2. Modeling and Predicting with Random Forest
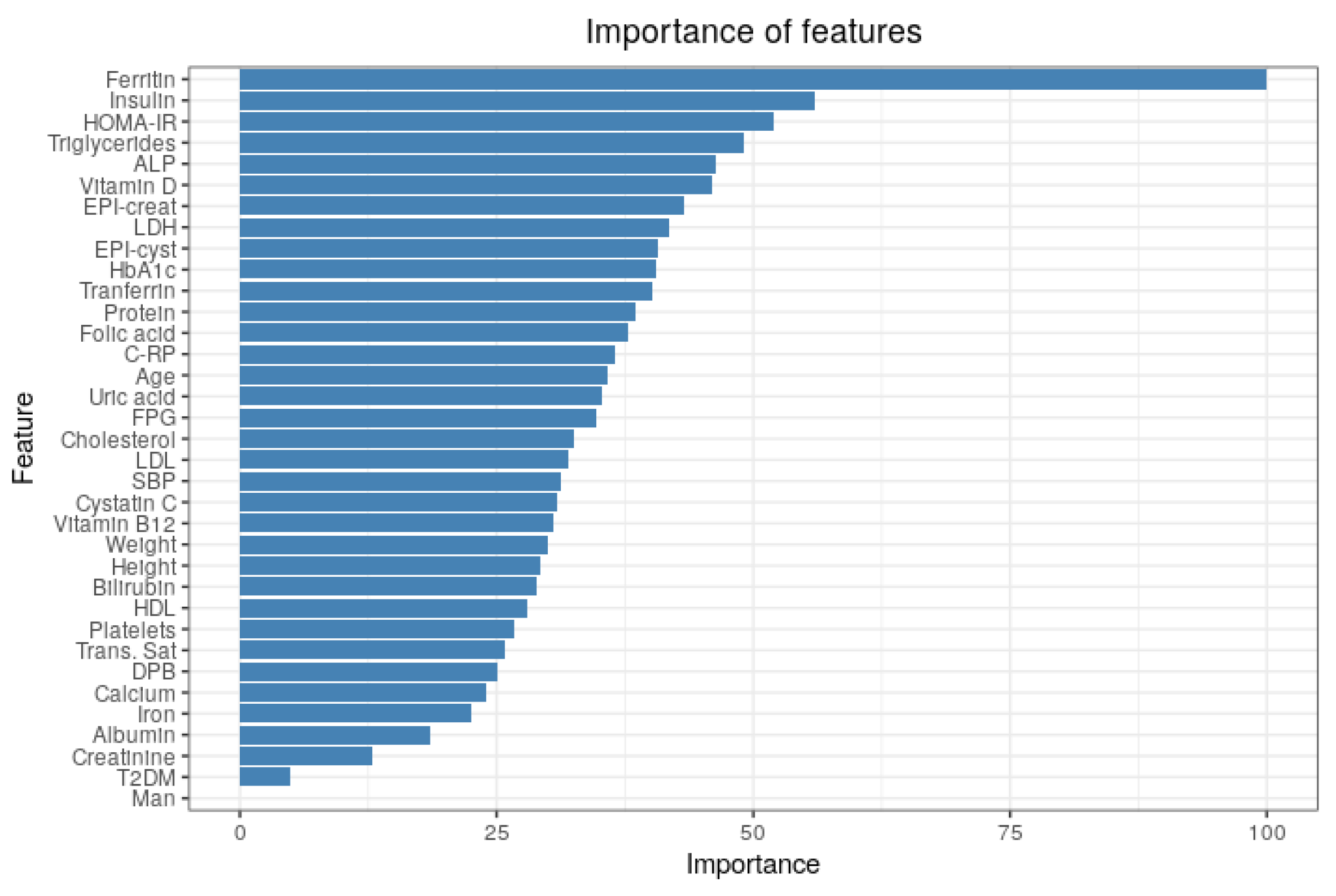
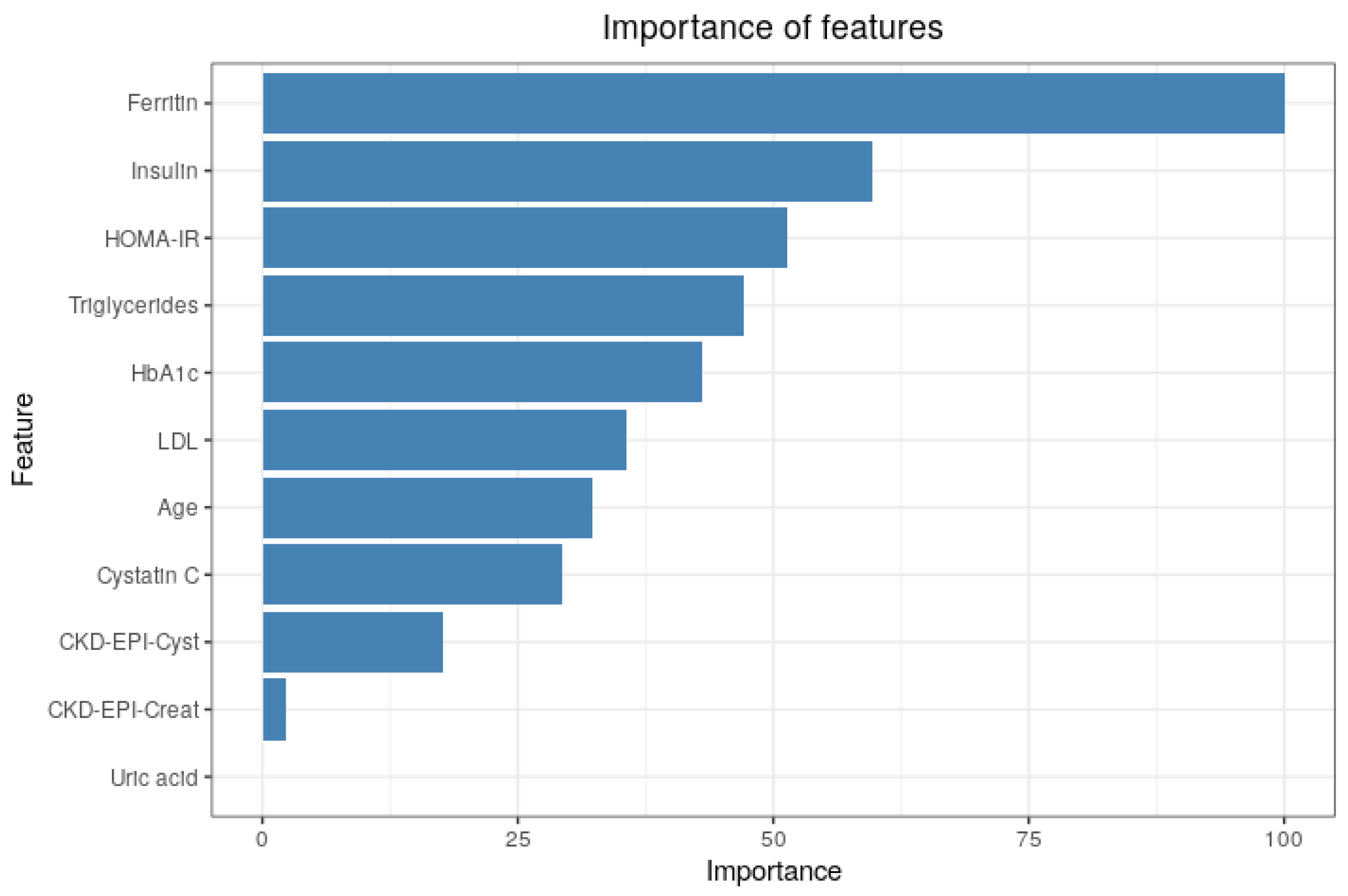
3.3. Importance of Features
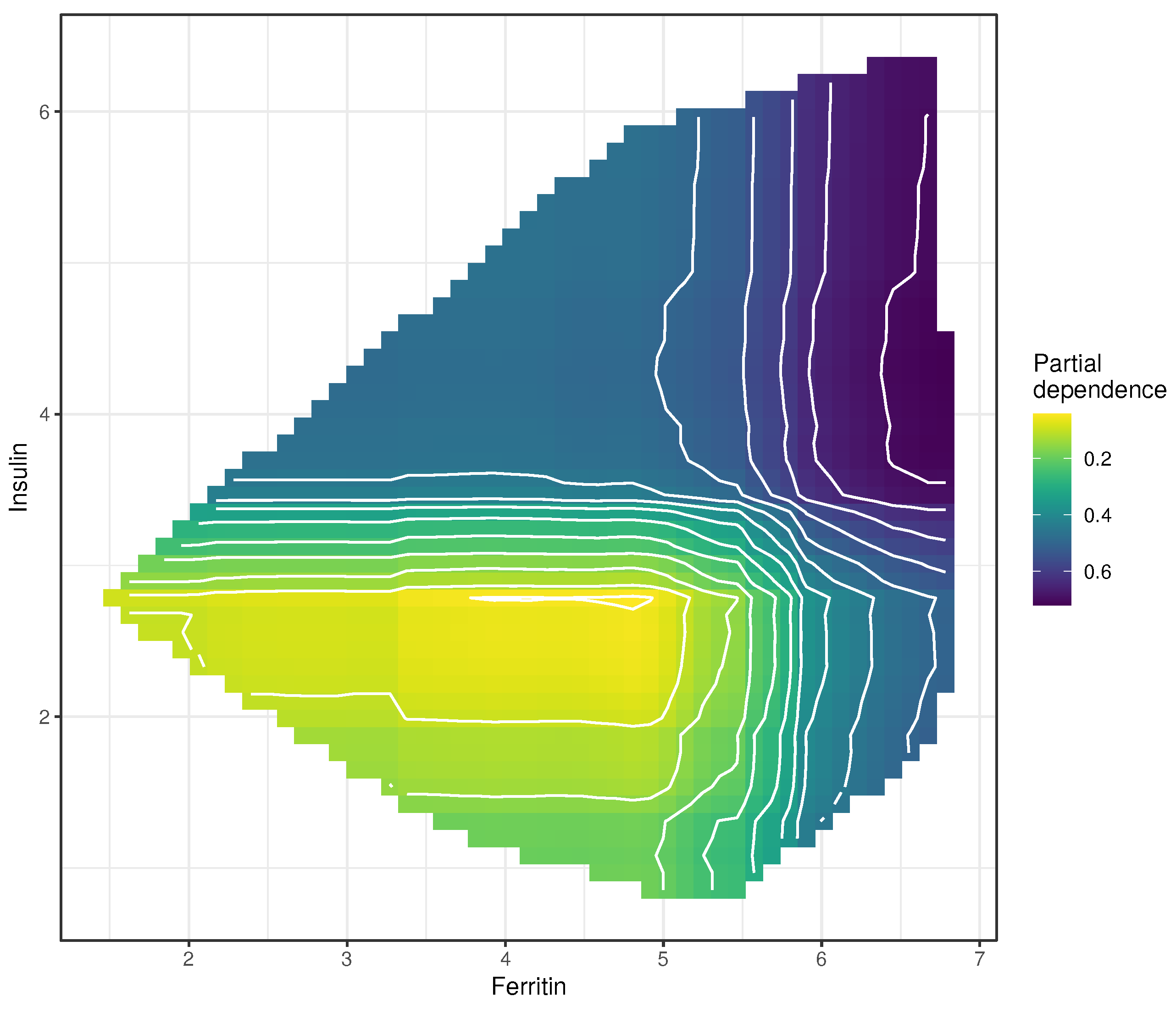
3.4. Partial Dependence Plots
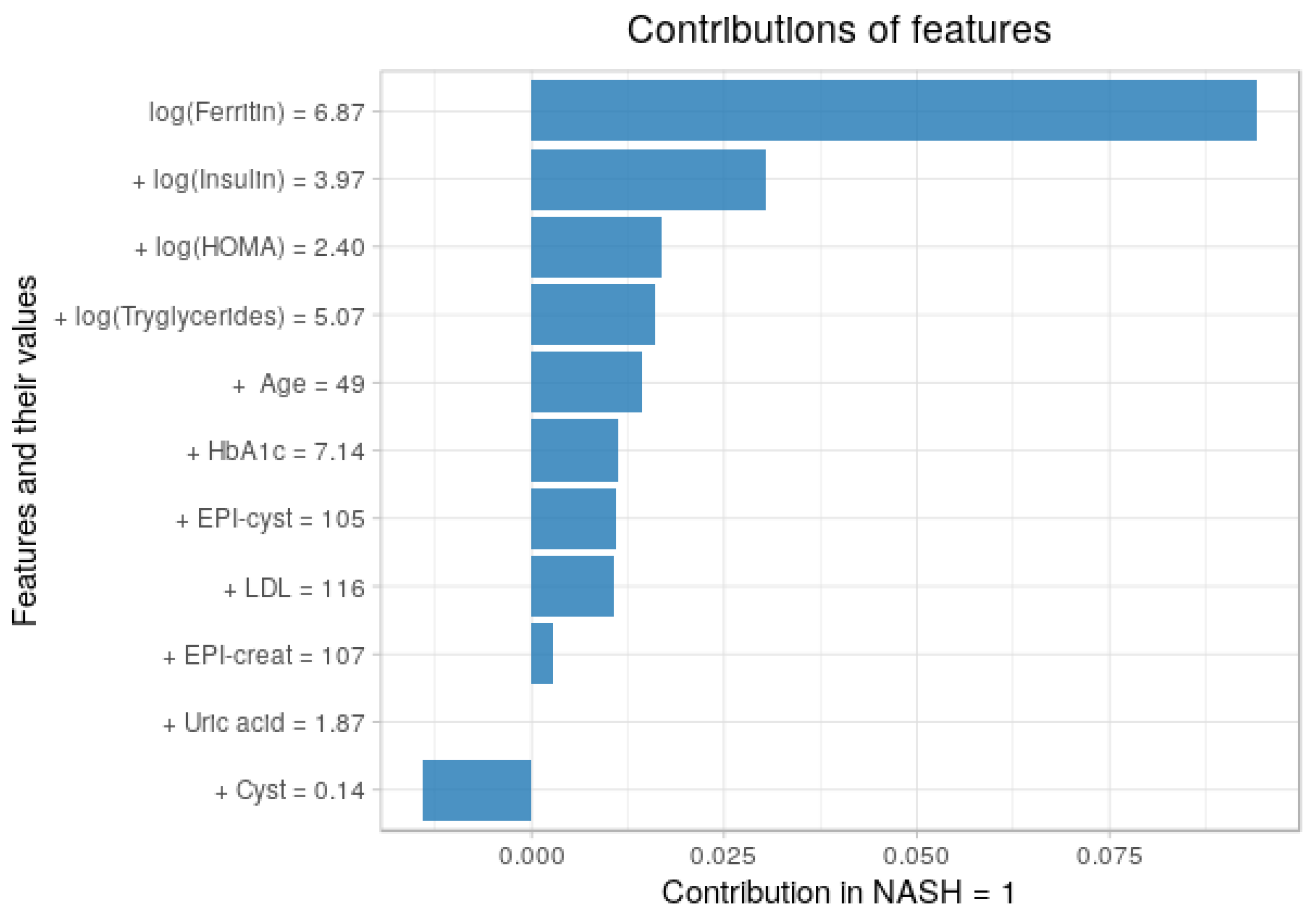
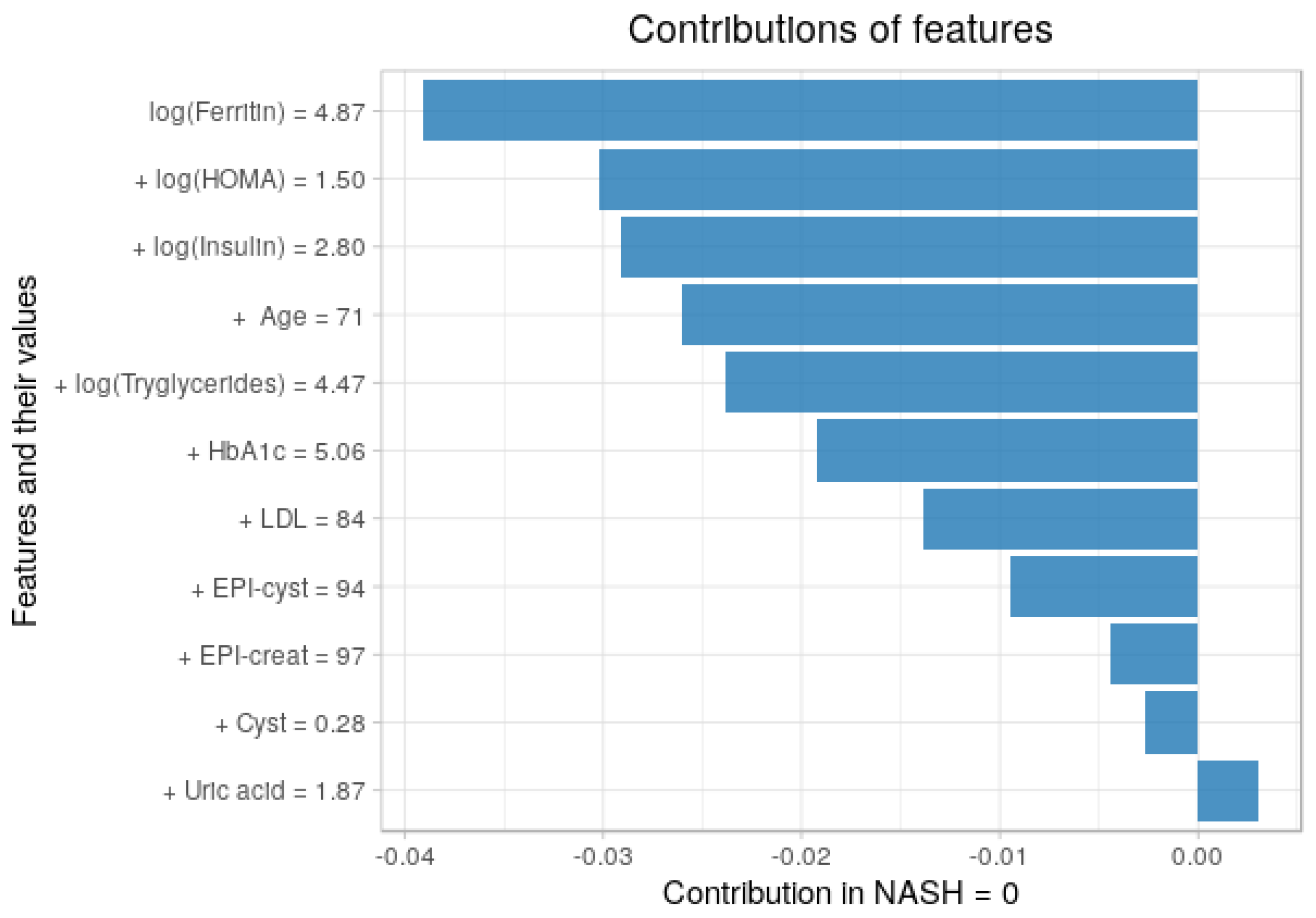
3.5. Contribution of Each Feature to the Predictions
4. Discussion
Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Angulo, P. Nonalcoholic fatty liver disease. N. Engl. J. Med. 2002, 346, 1221–1231. [Google Scholar] [CrossRef] [PubMed]
- Angulo, P.; Machado, M.V.; Diehl, A.M. Fibrosis in nonalcoholic Fatty liver disease: Mechanisms and clinical implications. Semin. Liver Dis. 2015, 35, 132–145. [Google Scholar] [CrossRef]
- Diehl, A.M.; Day, C. Cause, Pathogenesis, and Treatment of Nonalcoholic Steatohepatitis. N. Engl. J. Med. 2017, 377, 2063–2072. [Google Scholar] [CrossRef]
- Liangpunsakul, S.; Chalasani, N. Unexplained elevations in alanine aminotransferase in individuals with the metabolic syndrome: Results from the third National Health and Nutrition Survey (NHANES III). Am. J. Med. Sci. 2005, 329, 111–116. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. 4. Comprehensive Medical Evaluation and Assessment of Comorbidities: Standards of Medical Care in Diabetes—2020. Diabetes Care 2020, 43, S37–S47. [Google Scholar] [CrossRef] [PubMed]
- Pagadala, M.R.; McCullough, A.J. The relevance of liver histology to predicting clinically meaningful outcomes in nonalcoholic steatohepatitis. Clin. Liver Dis. 2012, 16, 487–504. [Google Scholar] [CrossRef] [PubMed]
- Cusi, K.; Orsak, B.; Bril, F.; Lomonaco, R.; Hecht, J.; Ortiz-Lopez, C.; Tio, F.; Hardies, J.; Darland, C.; Musi, N.; et al. Long-Term Pioglitazone Treatment for Patients With Nonalcoholic Steatohepatitis and Prediabetes or Type 2 Diabetes Mellitus: A Randomized Trial. Ann. Intern. Med. 2016, 165, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Cusi, K. Incretin-Based Therapies for the Management of Nonalcoholic Fatty Liver Disease in Patients with Type 2 Diabetes. Hepatology 2019, 69, 2318–2322. [Google Scholar] [CrossRef]
- Davison, B.A.; Harrison, S.A.; Cotter, G.; Alkhouri, N.; Sanyal, A.; Edwards, C.; Colca, J.R.; Iwashita, J.; Koch, G.G.; Dittrich, H.C. Suboptimal reliability of liver biopsy evaluation has implications for randomized clinical trials. J. Hepatol. 2020, 73, 1322–1332. [Google Scholar] [CrossRef]
- Lomonaco, R.; Godinez Leiva, E.; Bril, F.; Shrestha, S.; Mansour, L.; Budd, J.; Portillo Romero, J.; Schmidt, S.; Chang, K.L.; Samraj, G.; et al. Advanced Liver Fibrosis Is Common in Patients with Type 2 Diabetes Followed in the Outpatient Setting: The Need for Systematic Screening. Diabetes Care 2021, 44, 399–406. [Google Scholar] [CrossRef]
- Garcia-Carretero, R.; Vigil-Medina, L.; Barquero-Perez, O.; Ramos-Lopez, J. Relevant Features in Nonalcoholic Steatohepatitis Determined Using Machine Learning for Feature Selection. Metab. Syndr. Relat. Disord. 2019, 17, 444–451. [Google Scholar] [CrossRef] [PubMed]
- Chalasani, N.; Younossi, Z.; Lavine, J.E.; Charlton, M.; Cusi, K.; Rinella, M.; Harrison, S.A.; Brunt, E.M.; Sanyal, A.J. The diagnosis and management of nonalcoholic fatty liver disease: Practice guidance from the American Association for the Study of Liver Diseases. Hepatology 2018, 67, 328–357. [Google Scholar] [CrossRef] [PubMed]
- Mantovani, A.; Turino, T.; Lando, M.G.; Gjini, K.; Byrne, C.D.; Zusi, C.; Ravaioli, F.; Colecchia, A.; Maffeis, C.; Salvagno, G.; et al. Screening for non-alcoholic fatty liver disease using liver stiffness measurement and its association with chronic kidney disease and cardiovascular complications in patients with type 2 diabetes. Diabetes Metab. 2020, 46, 296–303. [Google Scholar] [CrossRef] [PubMed]
- Koehler, E.M.; Plompen, E.P.C.; Schouten, J.N.L.; Hansen, B.E.; Darwish Murad, S.; Taimr, P.; Leebeek, F.W.G.; Hofman, A.; Stricker, B.H.; Castera, L.; et al. Presence of diabetes mellitus and steatosis is associated with liver stiffness in a general population: The Rotterdam study. Hepatology 2016, 63, 138–147. [Google Scholar] [CrossRef]
- Lombardi, R.; Petta, S.; Pisano, G.; Dongiovanni, P.; Rinaldi, L.; Adinolfi, L.E.; Acierno, C.; Valenti, L.; Boemi, R.; Spatola, F.; et al. FibroScan Identifies Patients With Nonalcoholic Fatty Liver Disease and Cardiovascular Damage. Clin. Gastroenterol. Hepatol. Off. Clin. Pract. J. Am. Gastroenterol. Assoc. 2020, 18, 517–519. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Basu, S.; Kumbier, K.; Yu, B. A debiased MDI feature importance measure for random forests. arXiv 2019, arXiv:1906.10845. [Google Scholar]
- Taylor, R.S.; Taylor, R.J.; Bayliss, S.; Hagström, H.; Nasr, P.; Schattenberg, J.M.; Ishigami, M.; Toyoda, H.; Wong, V.W.S.; Peleg, N.; et al. Association between fibrosis stage and outcomes of patients with nonalcoholic fatty liver disease: A systematic review and meta-analysis. Gastroenterology 2020, 158, 1611–1625. [Google Scholar] [CrossRef]
- Spann, A.; Yasodhara, A.; Kang, J.; Watt, K.; Wang, B.; Goldenberg, A.; Bhat, M. Applying machine learning in liver disease and transplantation: A comprehensive review. Hepatology 2020, 71, 1093–1105. [Google Scholar] [CrossRef]
- Wong, G.L.H.; Yuen, P.C.; Ma, A.J.; Chan, A.W.H.; Leung, H.H.W.; Wong, V.W.S. Artificial intelligence in prediction of non-alcoholic fatty liver disease and fibrosis. J. Gastroenterol. Hepatol. 2021, 36, 543–550. [Google Scholar] [CrossRef] [PubMed]
- Sowa, J.P.; Heider, D.; Bechmann, L.P.; Gerken, G.; Hoffmann, D.; Canbay, A. Novel algorithm for non-invasive assessment of fibrosis in NAFLD. PLoS ONE 2013, 8, e62439. [Google Scholar] [CrossRef]
- Suresha, P.B.; Wang, Y.; Xiao, C.; Glass, L.; Yuan, Y.; Clifford, G.D. A deep learning approach for classifying nonalcoholic steatohepatitis patients from nonalcoholic fatty liver disease patients using electronic medical records. In Explainable AI in Healthcare and Medicine; Springer: Berlin/Heidelberg, Germany, 2021; pp. 107–113. [Google Scholar]
- Yip, T.F.; Ma, A.; Wong, V.S.; Tse, Y.K.; Chan, H.Y.; Yuen, P.C.; Wong, G.H. Laboratory parameter-based machine learning model for excluding non-alcoholic fatty liver disease (NAFLD) in the general population. Aliment. Pharmacol. Ther. 2017, 46, 447–456. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.H.; Chou, C.Y.; Hsiung, Y. Application of Machine Learning Methods to Predict Non-Alcohol Fatty Liver Disease in Taiwanese High-Tech Industry Workers. In Proceedings of the International Conference on Data Science (ICDATA), Shenzhen, China, 26–29 June 2017; The Steering Committee of The World Congress in Computer Science. Computer Engineering and Applied Computing: New York, NY, USA, 2017; pp. 118–123. [Google Scholar]
- Birjandi, M.; Ayatollahi, S.M.T.; Pourahmad, S.; Safarpour, A.R. Prediction and diagnosis of non-alcoholic fatty liver disease (NAFLD) and identification of its associated factors using the classification tree method. Iran. Red Crescent Med. J. 2016, 18, e32858. [Google Scholar] [CrossRef]
- Fialoke, S.; Malarstig, A.; Miller, M.R.; Dumitriu, A. Application of machine learning methods to predict non-alcoholic steatohepatitis (NASH) in non-alcoholic fatty liver (NAFL) patients. In Proceedings of the AMIA Annual Symposium, San Francisco, CA, USA, 3–7 November 2018; American Medical Informatics Association: Rockville, MD, USA, 2018; Volume 2018, p. 430. [Google Scholar]
- Docherty, M.; Regnier, S.A.; Capkun, G.; Balp, M.M.; Ye, Q.; Janssens, N.; Tietz, A.; Löffler, J.; Cai, J.; Pedrosa, M.C.; et al. Development of a novel machine learning model to predict presence of nonalcoholic steatohepatitis. J. Am. Med. Inform. Assoc. 2021, 28, 1235–1241. [Google Scholar] [CrossRef]
- American Diabetes Association. 2. Classification and Diagnosis of Diabetes: Standards of Medical Care in Diabetes—2018. Diabetes Care 2018, 41, S13–S27. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Chawla, N.V. Data Mining for Imbalanced Datasets: An Overview (Periodical Style); Department of Computer Science and Engineering, Notre Dame University: Notre Dame, IN, USA, 2005. [Google Scholar]
- Thai-Nghe, N.; Gantner, Z.; Schmidt-Thieme, L. Cost-sensitive learning methods for imbalanced data. In Proceedings of the 2010 IEEE International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Luque, A.; Carrasco, A.; Martín, A.; de las Heras, A. The impact of class imbalance in classification performance metrics based on the binary confusion matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; Astrophysics Source Code Library: Houghton, MI, USA, 2015; p. ascl-1505. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Palczewska, A.; Palczewski, J.; Robinson, R.M.; Neagu, D. Interpreting random forest classification models using a feature contribution method. In Integration of Reusable Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 193–218. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Saabas, A. Interpreting random forests. Diving Data 2014. Available online: https://blog.datadive.net/interpreting-randomforests/ (accessed on 1 May 2021).
- Staniak, M.; Biecek, P. Explanations of model predictions with live and breakDown packages. arXiv 2018, arXiv:1804.01955. [Google Scholar] [CrossRef]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Holgado-Cuadrado, R.; García-Carretero, R.; Barquero-Pérez, Ó. Análisis de la importancia de las características de la esteatohepatitis no alcohólica aplicando modelos Random Forest. In Proceedings of the XXXVIII Congreso Anual de la Sociedad Española de Ingeniería Biomédica, Valladolid, Spain, 25–27 November 2020; pp. 177–180. [Google Scholar]
- Garcia-Carretero, R.; Vigil-Medina, L.; Barquero-Perez, O. The Use of Machine Learning Techniques to Determine the Predictive Value of Inflammatory Biomarkers in the Development of Type 2 Diabetes Mellitus. Metab. Syndr. Relat. Disord. 2021. [Google Scholar] [CrossRef]
- Konijn, A.M. Iron metabolism in inflammation. Bailliere’s Clin. Haematol. 1994, 7, 829–849. [Google Scholar] [CrossRef]
- Ford, E.S.; Cogswell, M.E. Diabetes and serum ferritin concentration among U.S. adults. Diabetes Care 1999, 22, 1978–1983. [Google Scholar] [CrossRef] [PubMed]
- Kowdley, K.V.; Belt, P.; Wilson, L.A.; Yeh, M.M.; Neuschwander-Tetri, B.A.; Chalasani, N.; Sanyal, A.J.; Nelson, J.E. Serum ferritin is an independent predictor of histologic severity and advanced fibrosis in patients with nonalcoholic fatty liver disease. Hepatology 2012, 55, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Du, S.X.; Lu, L.L.; Geng, N.; Victor, D.W.; Chen, L.Z.; Wang, C.; Yue, H.Y.; Xin, Y.N.; Xuan, S.Y.; Jin, W.W. Association of serum ferritin with non-alcoholic fatty liver disease: A meta-analysis. Lipids Health Dis. 2017, 16, 228. [Google Scholar] [CrossRef]
- Utzschneider, K.M.; Kahn, S.E. Review: The role of insulin resistance in nonalcoholic fatty liver disease. J. Clin. Endocrinol. Metab. 2006, 91, 4753–4761. [Google Scholar] [CrossRef]
- Pagano, G.; Pacini, G.; Musso, G.; Gambino, R.; Mecca, F.; Depetris, N.; Cassader, M.; David, E.; Cavallo-Perin, P.; Rizzetto, M. Nonalcoholic steatohepatitis, insulin resistance, and metabolic syndrome: Further evidence for an etiologic association. Hepatology 2002, 35, 367–372. [Google Scholar] [CrossRef]
- Alam, S.; Mustafa, G.; Alam, M.; Ahmad, N. Insulin resistance in development and progression of nonalcoholic fatty liver disease. World J. Gastrointest. Pathophysiol. 2016, 7, 211–217. [Google Scholar] [CrossRef]
- Liu, S.T.; Su, K.Q.; Zhang, L.H.; Liu, M.H.; Zhao, W.X. Hypoglycemic agents for non-alcoholic fatty liver disease with type 2 diabetes mellitus: A protocol for systematic review and network meta-analysis. Medicine 2020, 99, e21568. [Google Scholar] [CrossRef]
- Harrison, S.A.; Gawrieh, S.; Roberts, K.; Lisanti, C.J.; Schwope, R.B.; Cebe, K.M.; Paradis, V.; Bedossa, P.; Aldridge Whitehead, J.M.; Labourdette, A.; et al. Prospective evaluation of the prevalence of non-alcoholic fatty liver disease and steatohepatitis in a large middle-aged US cohort. J. Hepatol. 2021. [Google Scholar] [CrossRef]
- Castera, L. Noninvasive Evaluation of Nonalcoholic Fatty Liver Disease. Semin. Liver Dis. 2015, 35, 291–303. [Google Scholar] [CrossRef] [PubMed]
- Golabi, P.; Sayiner, M.; Fazel, Y.; Koenig, A.; Henry, L.; Younossi, Z.M. Current complications and challenges in nonalcoholic steatohepatitis screening and diagnosis. Expert Rev. Gastroenterol. Hepatol. 2016, 10, 63–71. [Google Scholar] [CrossRef] [PubMed]


| Feature Name | Type | Measurement Unit | Skewness |
|---|---|---|---|
| Age | numeric | years | no |
| Sex | categorical | Men, Woman | |
| Weight | numeric | kg | no |
| Height | numeric | centimeters | no |
| Systolic blood pressure (SBP) | numeric | mmHg | no |
| Diastolic blood pressure (DBP) | numeric | mmHg | no |
| Vitamin D | numeric | ng/dL | no |
| Folic acid | numeric | ng/dL | no |
| Serum albumin | numeric | g/dL | no |
| Bilirubin | numeric | mg/dL | left-skewed |
| Serum calcium | numeric | mg/dL | left-skewed |
| Creatine phosphokinase (CPK) | numeric | mg/dL | left-skewed |
| Cholesterol | numeric | mg/dL | left-skewed |
| LDL-cholesterol | numeric | mg/dL | left-skewed |
| HDL-cholesterol | numeric | mg/dL | left-skewed |
| Triglycerides | numeric | mg/dL | left-skewed |
| Alkaline phosphatase (ALP) | numeric | IU/L | left-skewed |
| Serum iron | numeric | μg/dL | no |
| Ferritin | numeric | mg/dL | left-skewed |
| Transferrin saturation percentage | numeric | percentage | no |
| Gamma-glutamyl transferase (GGT) | numeric | mg/dL | left-skewed |
| HOMA-IR | numeric | NA | left-skewed |
| Insulin | numeric | μU/mL | left-skewed |
| Glycated hemoglobin (HbA1c) | numeric | percentage | left-skewed |
| Fasting plasma glucose (FPG) | numeric | mg/dL | left-skewed |
| Lactate dehydrogenase (LDH) | numeric | IU/L | no |
| Platelet count | numeric | cells per mL | left-skewed |
| Serum proteins | numeric | g/dL | left-skewed |
| Uric acid | numeric | mg/dL | left-skewed |
| Vitamin B12 | numeric | ng/L | no |
| Creatinine | numeric | mg/dL | left-skewed |
| Cystatin C | numeric | mg/dL | left-skewed |
| C-reactive protein (CRP) | numeric | mg/L | left-skewed |
| Body mass index (BMI) | numeric | kg/m2 | no |
| CKD-EPI-Creatinine | numeric | mL/min/1.72 m2 | no |
| CKD-EPI-Cystatnin C | numeric | mL/min/1.72 m2 | no |
| Type 2 diabetes mellitus (T2DM) | Boolean | 0.1 | |
| Nonalcoholic steatohepatitis (NASH) | Boolean | 0.1 |
| Total | With NASH | Without NASH | p Value | |
|---|---|---|---|---|
| Patients | 1525 | 507 | 1018 | |
| Sex (men) | 48.9 | 42.4 | 52.1 | 0.2 |
| Age | 57.3 ± 13.4 | 54.8 ± 11.6 | 58.5 ± 14.0 | <0.001 |
| Weight | 78.3 ± 15.1 | 81.0 ± 15.6 | 77.6 ± 14.9 | <0.001 |
| Height | 161.3 ± 14.4 | 162.9 ± 11.0 | 160.2 ± 30.2 | 0.3 |
| SBP (mmHg) | 146.8 ± 20.0 | 148.0 ± 19.8 | 146.2 ± 20.1 | 0.174 |
| DBP (mmHg) | 85.6 ± 11.2 | 87.6 ± 10.9 | 84.6 ± 11.2 | <0.001 |
| Vitamin D | 18.0 ± 6.7 | 17.9 ± 7.1 | 18.1 ± 6.5 | 0.32 |
| Folic acid | 14.0 ± 5.9 | 13.8 ± 6.0 | 14.2 ± 5.8 | 0.96 |
| Serum albumin | 4.1 ± 0.4 | 4.1 ± 0.5 | 4.1 ± 0.4 | 0.552 |
| Bilirubin | 0.8 (0.5) | 0.9 (0.4) | 0.8 (0.5) | <0.001 |
| Serum calcium | 10.2 (0.5) | 10.3 (0.6) | 10.2 (0.5) | <0.001 |
| CPK | 146.0 (118.0) | 180.0 (173.5) | 143.0 (91.8) | <0.001 |
| Cholesterol | 224.3 (40.0) | 231.3 (46.0) | 220.8 (36.2) | <0.001 |
| LDL | 139.0 (32.0) | 144.6 (33.5) | 136.2 (30.9) | <0.001 |
| HDL | 67.8 (18.9) | 67.1 (20.5) | 68.1 (18.0) | 0.29 |
| Triglycerides | 167.0 (118.0) | 194.0 (138.0 | 152.0 (104.0 | <0.001 |
| ALP | 86.0 (32.0) | 90.0 (36.5) | 84.0 (32.8) | <0.001 |
| Serum iron | 56.6 ± 23.3 | 54.9 ± 21.0 | 57.5 ± 24.4 | 0.139 |
| Ferritin | 185.0 (176.2) | 247.0 (238.0) | 162.0 (136.0) | <0.001 |
| Transferrin sat. (%) | 13.2 (7.7) | 12.5 (8.2) | 13.2 (7.5) | 0.33 |
| GGT | 38.0 (46.0) | 63.0 (80.0) | 31.0 (29.0 | <0.001 |
| HOMA-IR | 4.5 (2.9) | 5.2 (5.2) | 4.5 (1.9) | <0.001 |
| Insulin | 16.5 (9.2) | 18.5 (16.0) | 16.5 (6.3) | <0.001 |
| HbA1c (%) | 6.2 (1.0) | 6.3 (1.7) | 6.2 (0.8) | <0.001 |
| FPG | 117.0 (42.0) | 127.0 (64.0) | 114.0 (36.0) | <0.001 |
| LDH | 300.9 ± 86.7 | 309.2 ± 93.1 | 296.8 ± 83.0 | 0.17 |
| Platelet count | 288.0 (94.0) | 293.0 (85.0) | 284.5 (97.0) | 0.137 |
| Serum proteins | 7.70 (0.5) | 7.76 (0.5) | 7.6 (0.6) | 0.223 |
| Uric Acid | 7.2 (2.7) | 7.7 (3.5) | 6.9 (2.2) | <0.001 |
| Vitamin B12 | 451.6 ± 152.2 | 470.0 ± 159.8 | 442.4 ± 147.4 | 0.3 |
| Creatinine | 0.8 (0.2) | 0.8 (0.3) | 0.8 (0.2) | 0.9 |
| Cystatin C | 0.7 (0.2) | 0.7 (0.2) | 0.8 (0.2) | <0.001 |
| C-RP | 8.7 (15.1) | 10.8 (15.5) | 7.7 (13.9) | <0.001 |
| CKD-EPI-Creatinine | 92.8 ± 18.5 | 97.5 ± 15.8 | 90.4 ± 19.3 | <0.001 |
| CKD-EPI-Cystatin C | 101.5 ± 22.5 | 107.5 ± 20.3 | 98.6 ± 23.0 | <0.001 |
| T2DM (%) | 43.3 | 54.7 | 37.6 | <0.001 |
| No Preprocessing | Preprocessing Methods | |||||
|---|---|---|---|---|---|---|
| No Imbalance Method | Class Weighting | Undersampling | Oversampling | Parsimonious Model | ||
| Accuracy | 0.872 | 0.869 | 0.872 | 0.796 | 0.865 | 0.867 |
| Sensitivity | 0.642 | 0.715 | 0.728 | 0.794 | 0.741 | 0.702 |
| Specificity | 0.966 | 0.947 | 0.943 | 0.798 | 0.927 | 0.950 |
| Precision | 0.906 | 0.869 | 0.874 | 0.886 | 0.877 | 0.864 |
| F1-score | 0.751 | 0.806 | 0.807 | 0.739 | 0.801 | 0.805 |
| AUC | 0.837 | 0.831 | 0.836 | 0.796 | 0.834 | 0.829 |
| EER | 0.162 | 0.168 | 0.162 | 0.207 | 0.165 | 0.147 |
| No Imbalance Method | Class Weighting | Undersampling | Oversampling | Parsimonious Model | |
|---|---|---|---|---|---|
| No preprocessing | Z = 0.946 p-value = 0.343 | Z = 0 p-value = 1 | Z = 3.170 p-value = 0.001 | Z = 0.391 p-value = 0.695 | Z = −1.235 p-value = 0.216 |
| No Imbalance Method | Z = −1.070 p-value = 0.284 | Z = 2.505 p-value = 0.012 | Z = −0.430 p-value = 0.666 | Z = −1.870 p-value = 0.061 | |
| Class Weighting | Z = 3.068 p-value = 0.002 | Z = 0.537 p-value = 0.591 | Z = −1.408 p-value = 0.160 | ||
| Undersampling | Z = −2.904 p-value = 0.003 | Z = −3.601 p-value = 0.003 | |||
| Oversampling | Z = −1.64 p-value = 0.101 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Carretero, R.; Holgado-Cuadrado, R.; Barquero-Pérez, Ó. Assessment of Classification Models and Relevant Features on Nonalcoholic Steatohepatitis Using Random Forest. Entropy 2021, 23, 763. https://doi.org/10.3390/e23060763
García-Carretero R, Holgado-Cuadrado R, Barquero-Pérez Ó. Assessment of Classification Models and Relevant Features on Nonalcoholic Steatohepatitis Using Random Forest. Entropy. 2021; 23(6):763. https://doi.org/10.3390/e23060763
Chicago/Turabian StyleGarcía-Carretero, Rafael, Roberto Holgado-Cuadrado, and Óscar Barquero-Pérez. 2021. "Assessment of Classification Models and Relevant Features on Nonalcoholic Steatohepatitis Using Random Forest" Entropy 23, no. 6: 763. https://doi.org/10.3390/e23060763
APA StyleGarcía-Carretero, R., Holgado-Cuadrado, R., & Barquero-Pérez, Ó. (2021). Assessment of Classification Models and Relevant Features on Nonalcoholic Steatohepatitis Using Random Forest. Entropy, 23(6), 763. https://doi.org/10.3390/e23060763







