Detecting and Analyzing Politically-Themed Stocks Using Text Mining Techniques and Transfer Entropy—Focus on the Republic of Korea’s Case
Abstract
1. Introduction
2. Data and Methodology
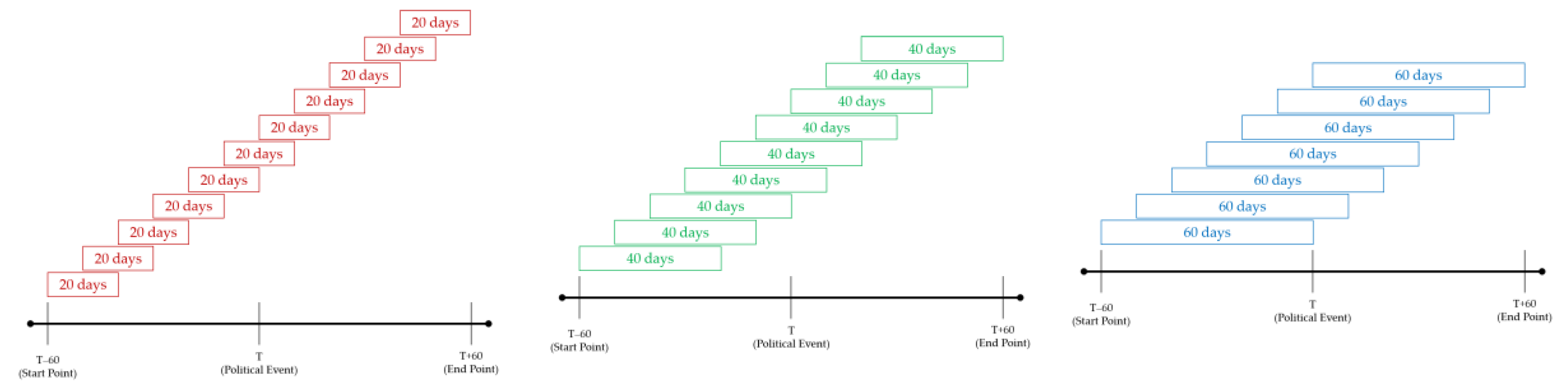
2.1. Research Period
2.2. Data
2.2.1. Politician-Related Data
2.2.2. Text Data
2.2.3. Abnormal Return Data
2.2.4. Preliminary Analysis
2.3. Methodology
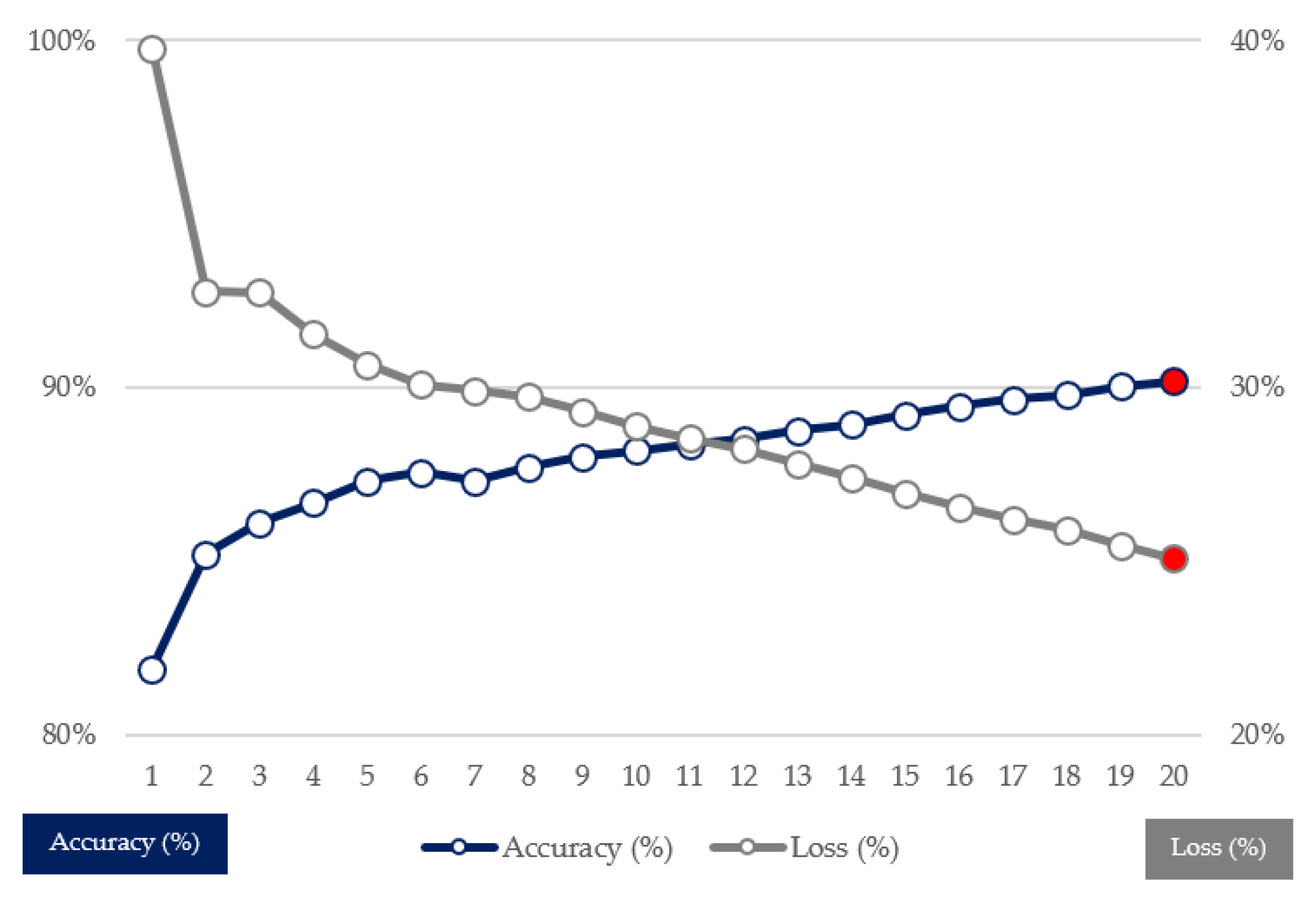
2.3.1. Sentiment Analysis
2.3.2. Transfer Entropy
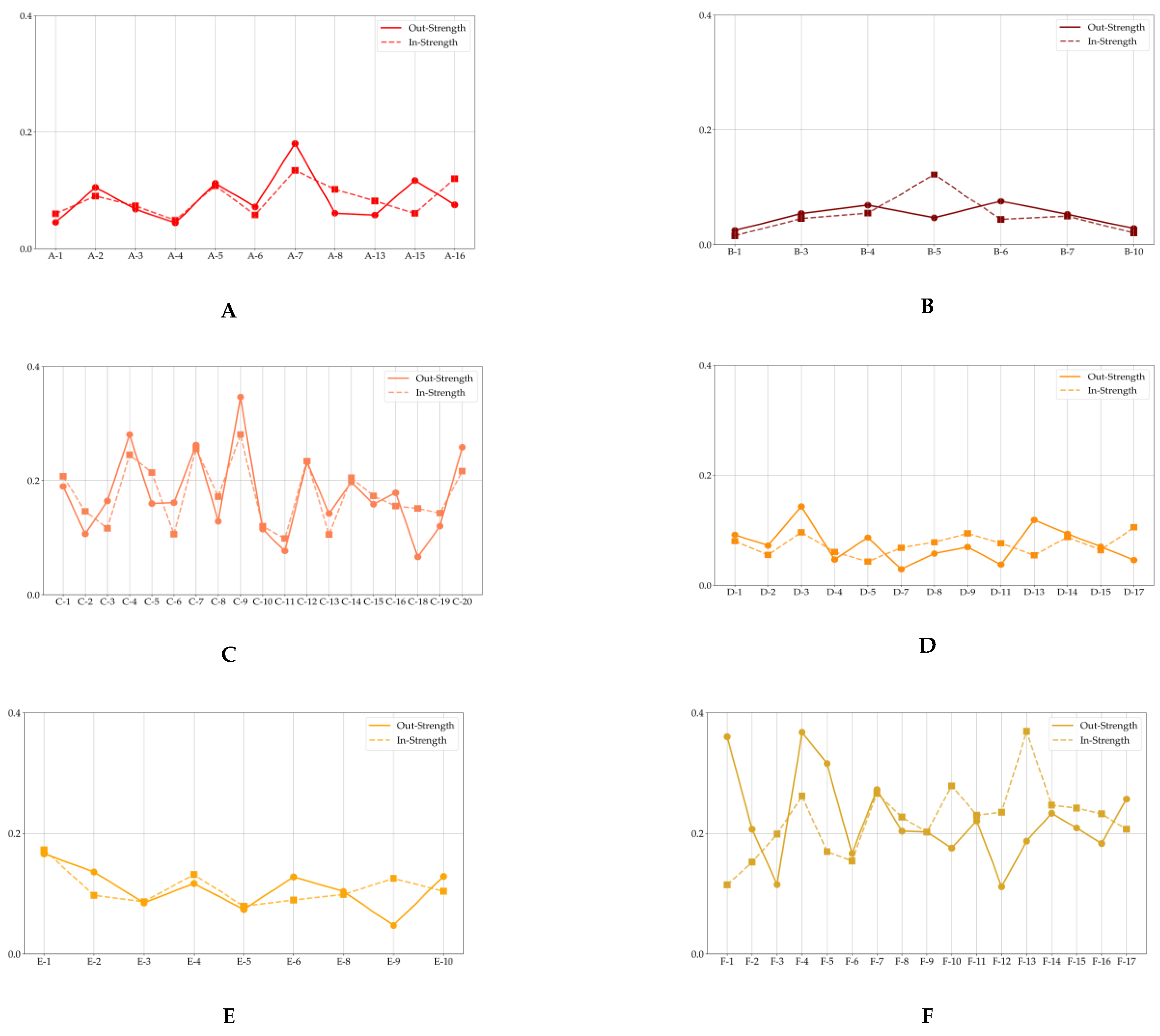
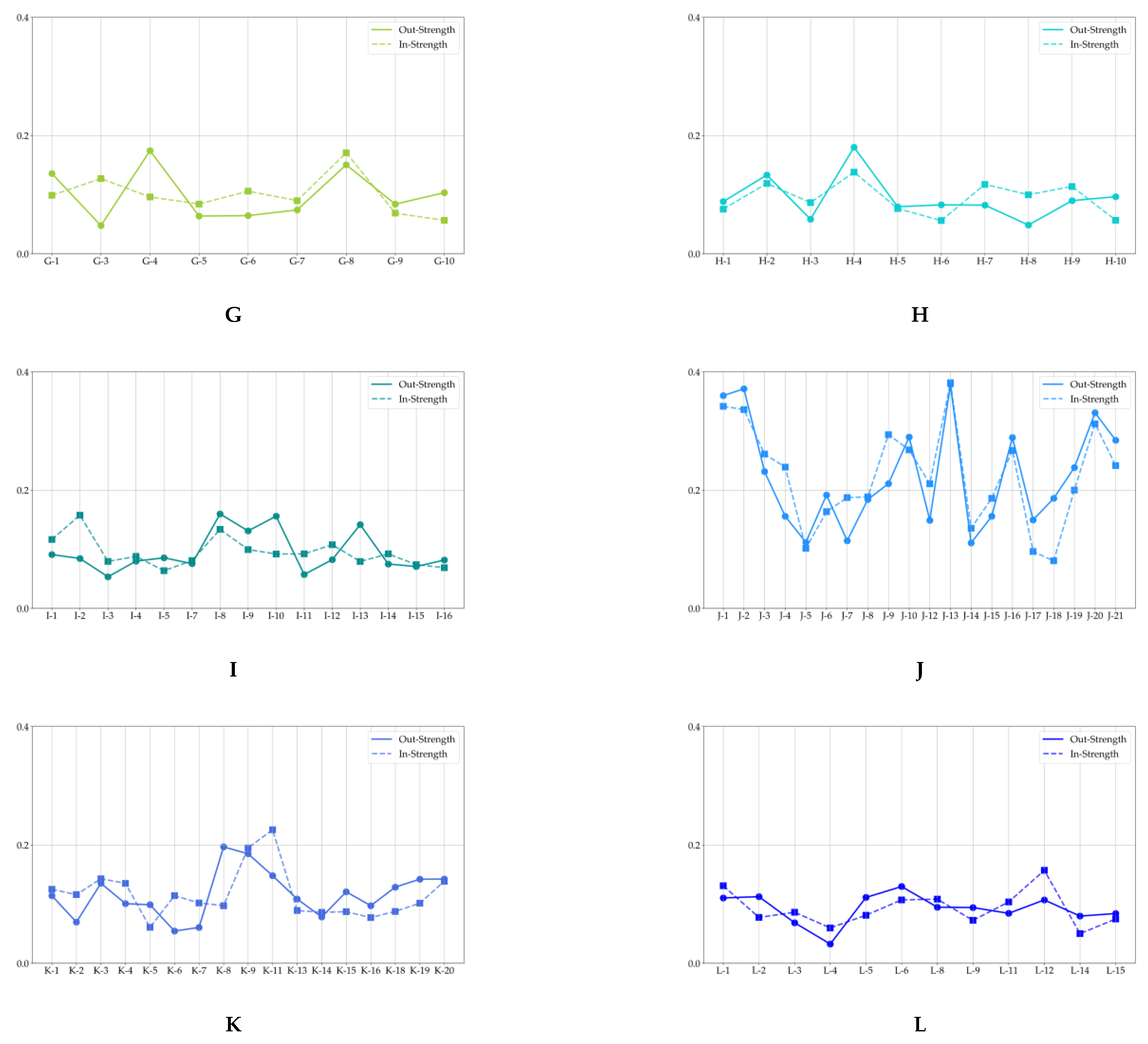
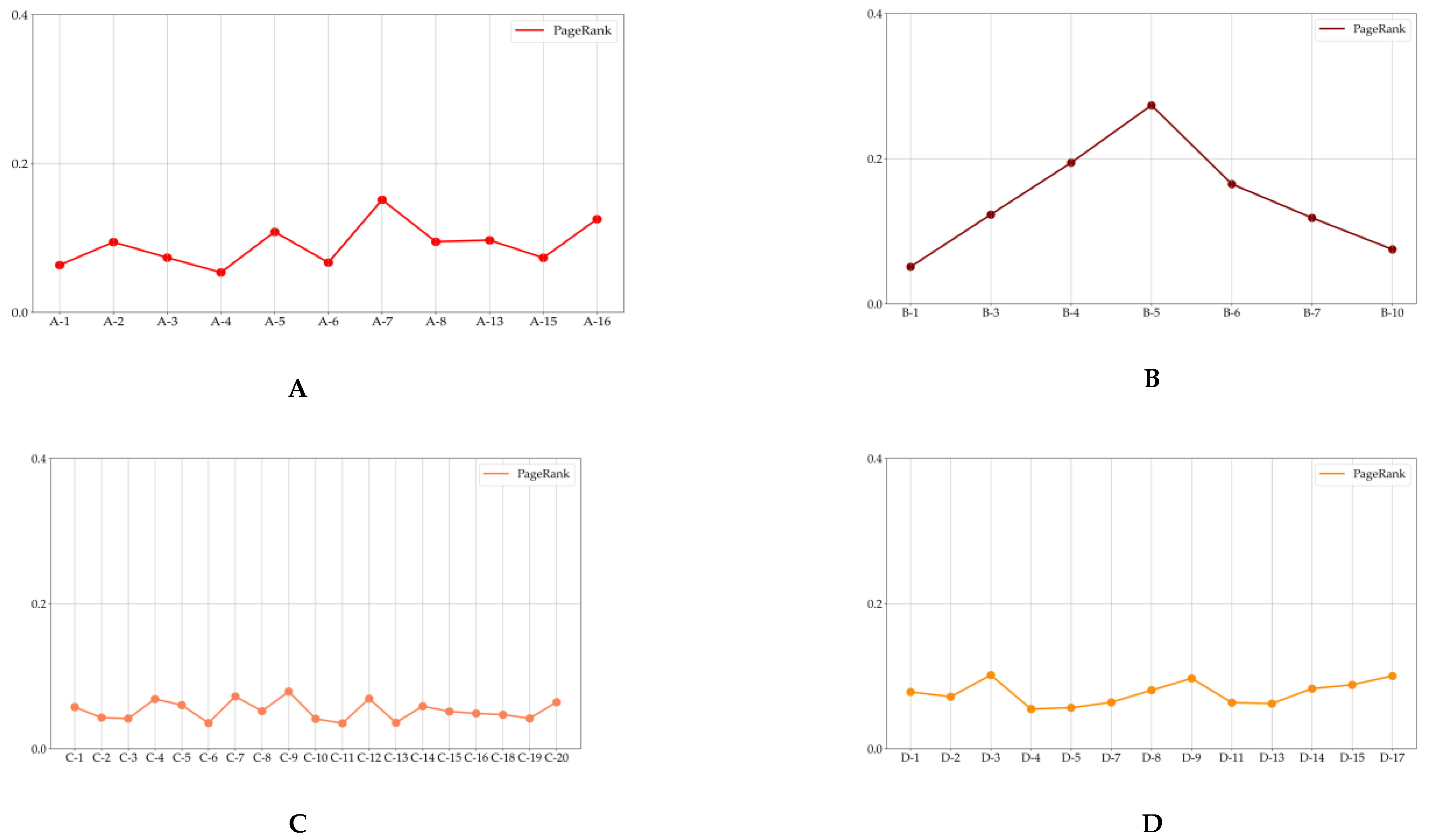
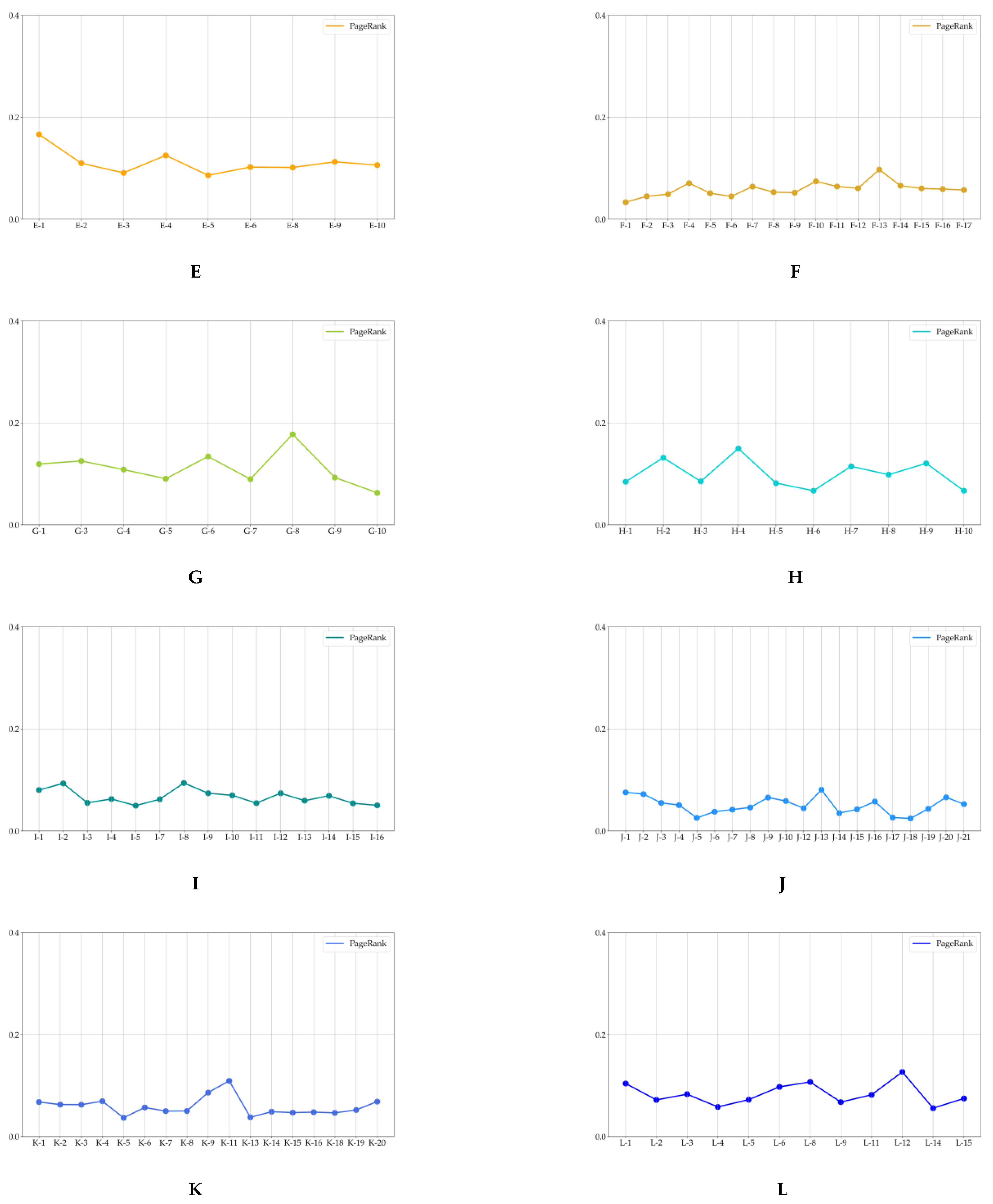
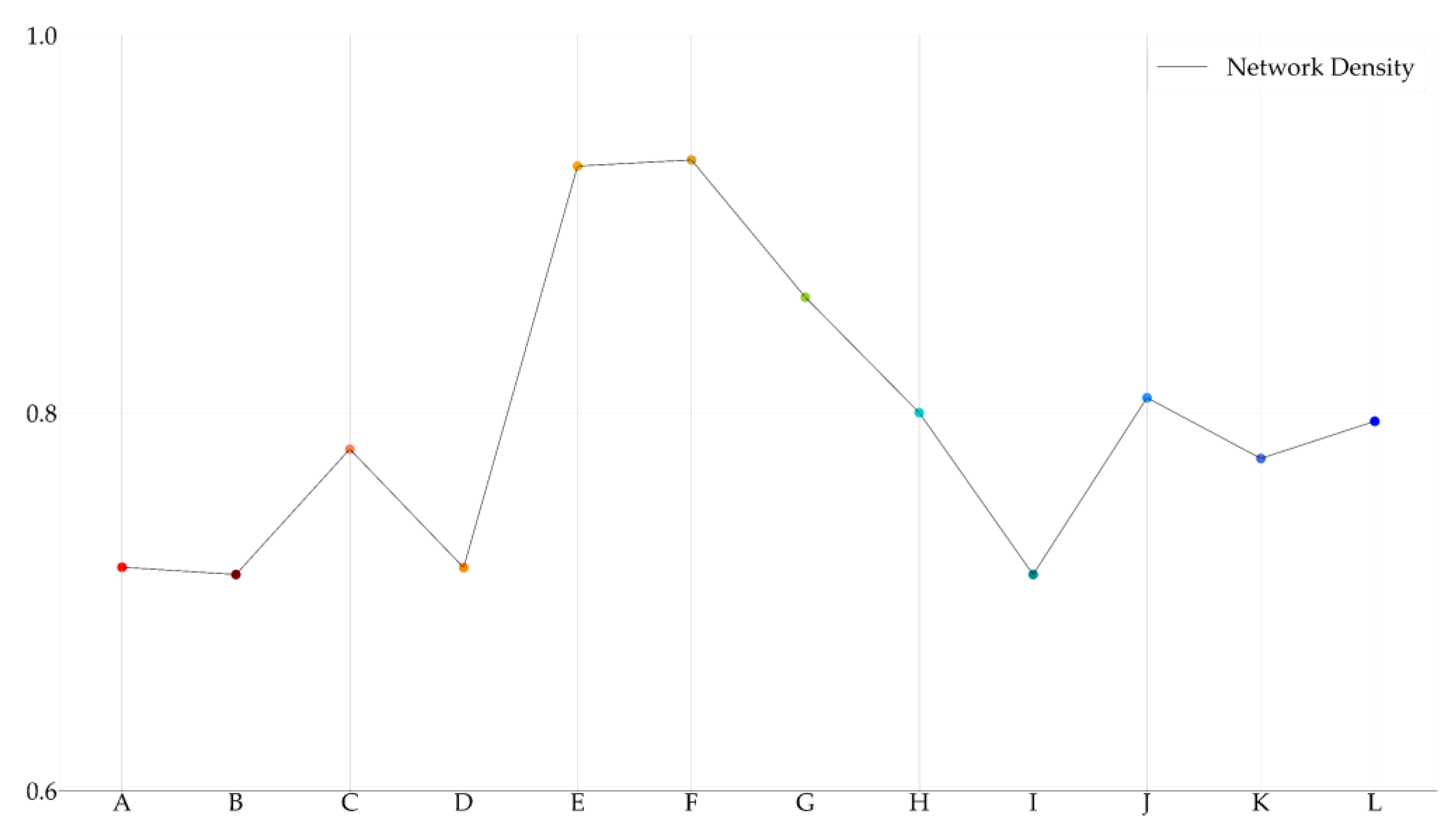
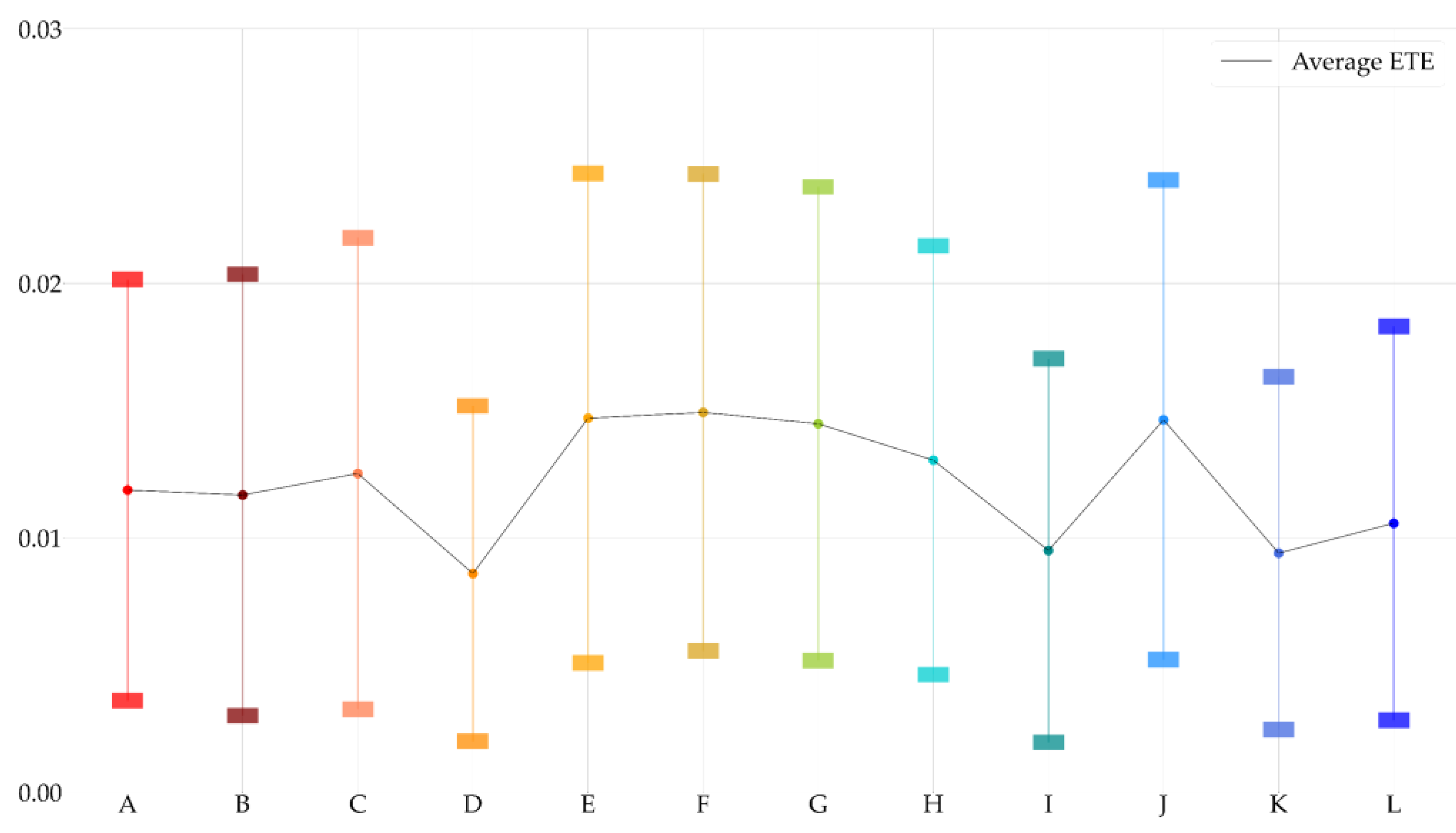
2.3.3. Complex Network Analysis
- (1).
- Network Density (ND)
- (2).
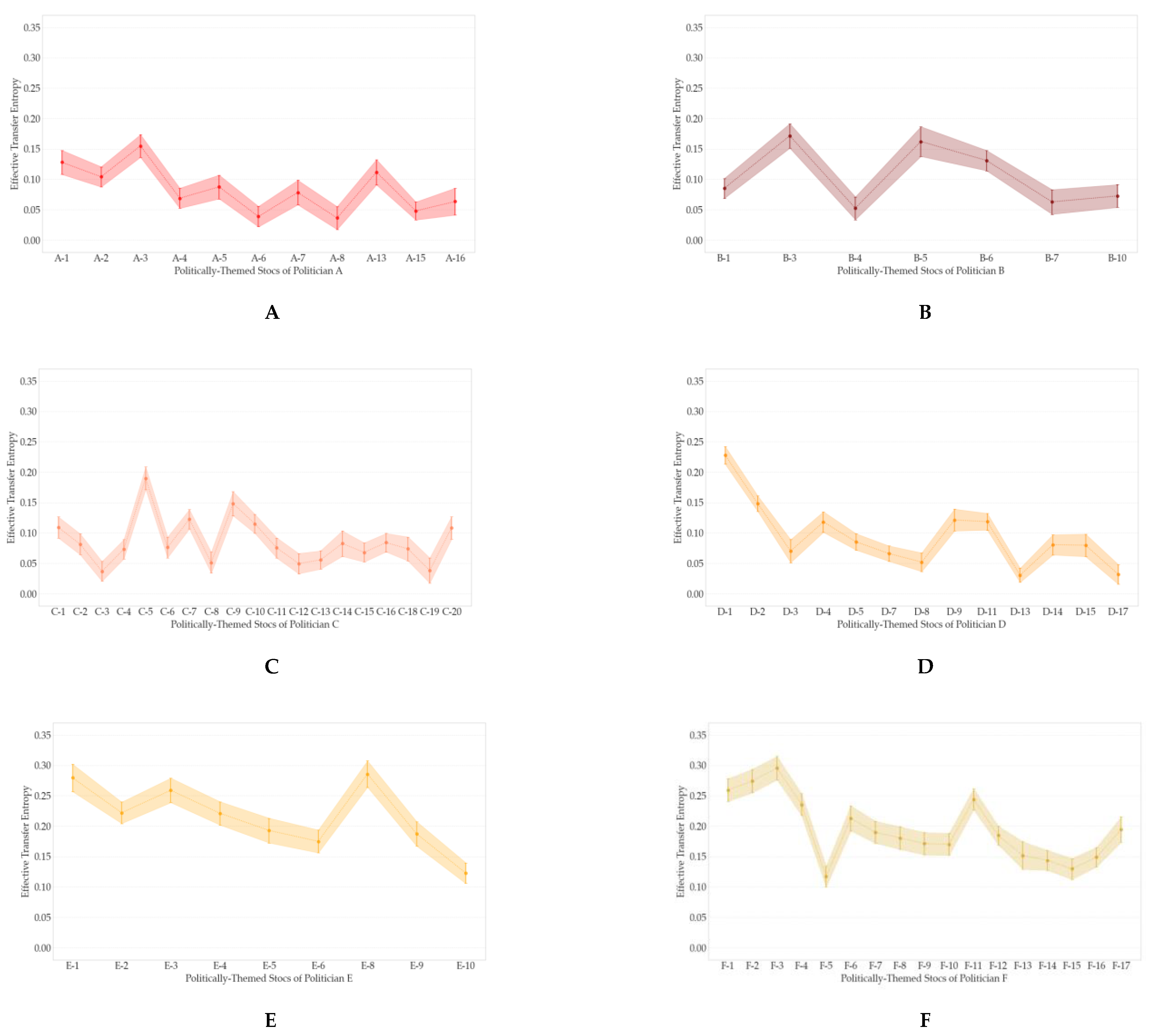
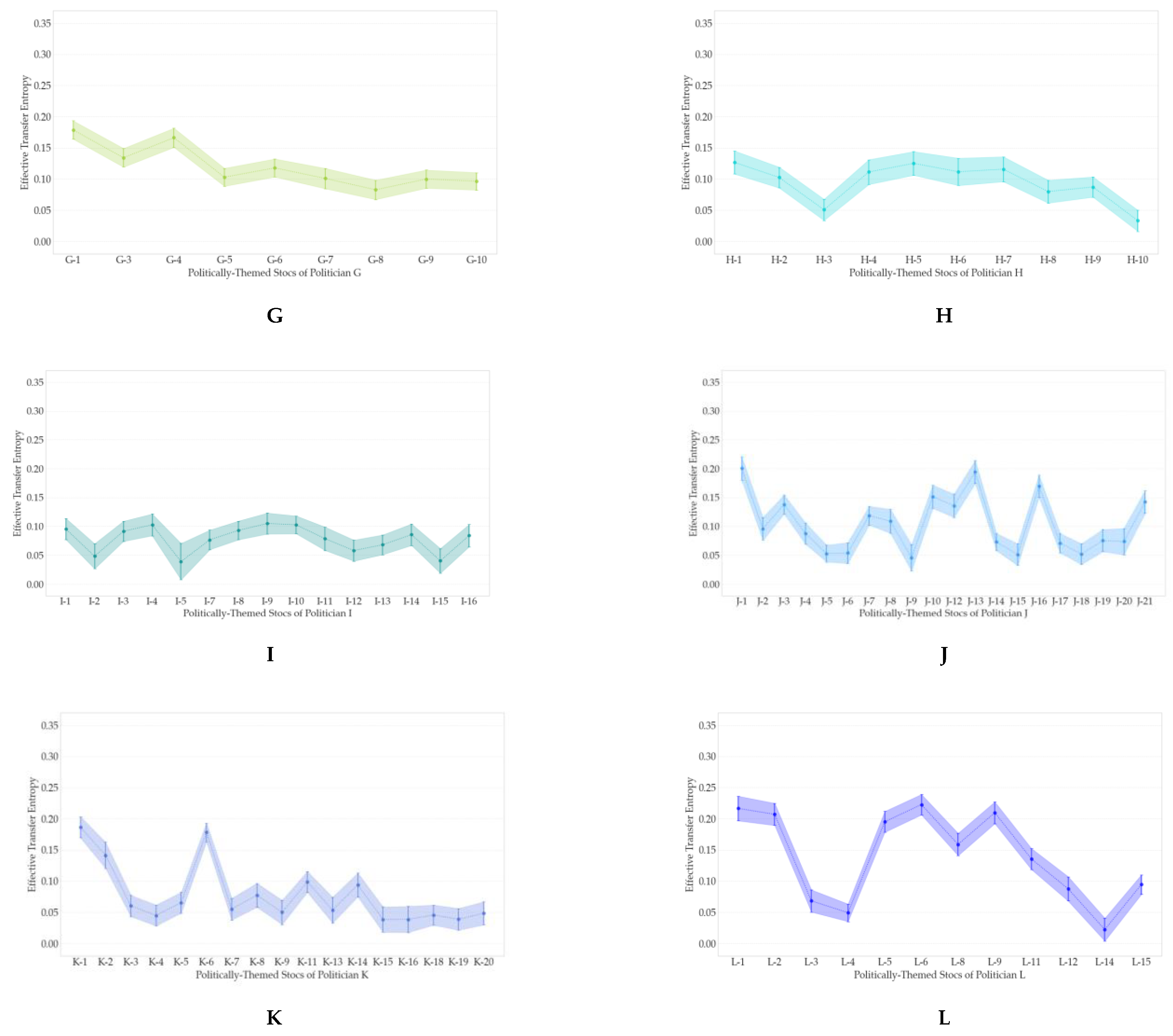
- Average Effective Transfer Entropy
- (3).
- Degree Centrality
- (4).
- Node Strength
- (5).
- PageRank
3. Empirical Analysis
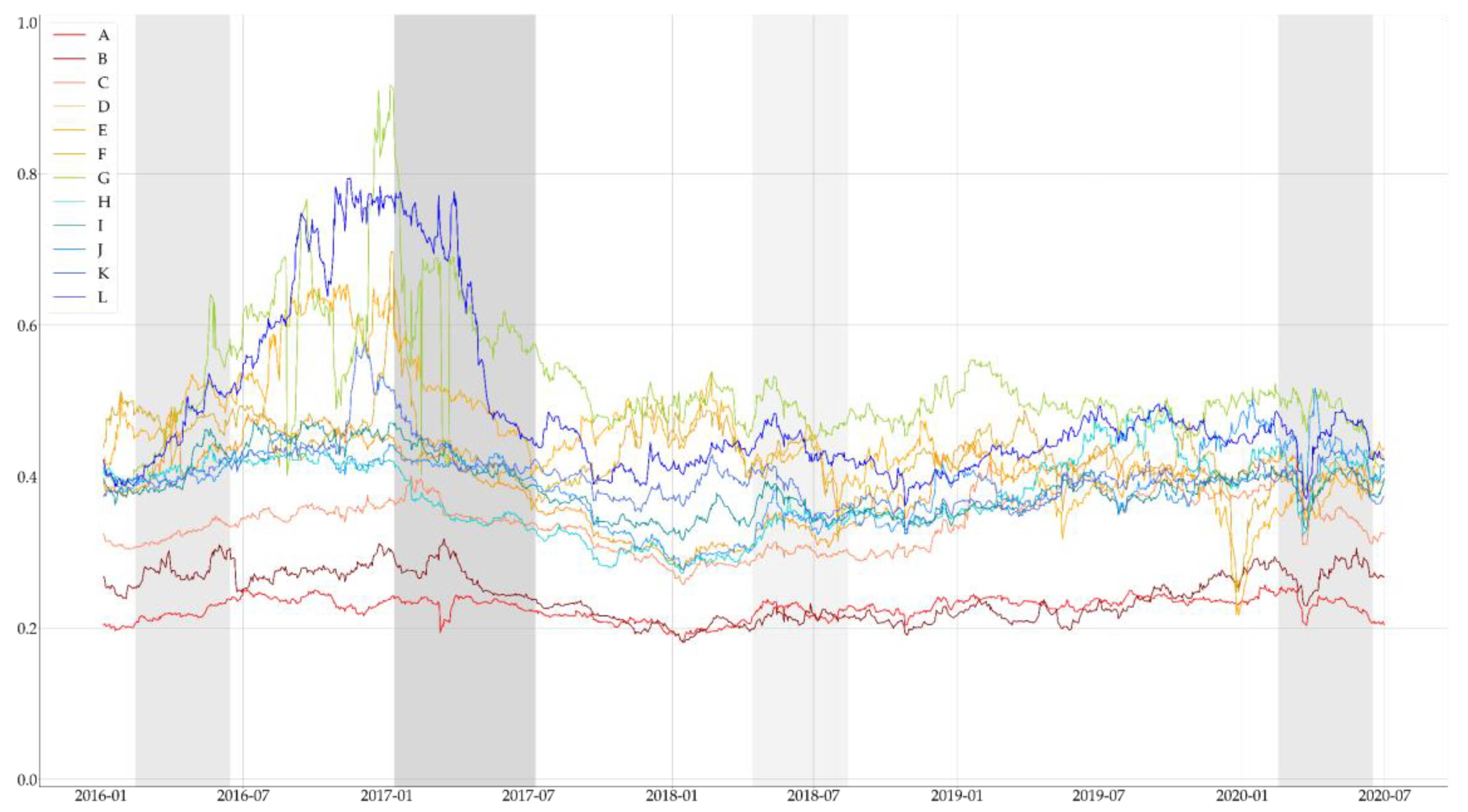
3.1. Calculating the Politician Sentiment Index (PSI)
3.2. Selecting Politically-Themed Stocks
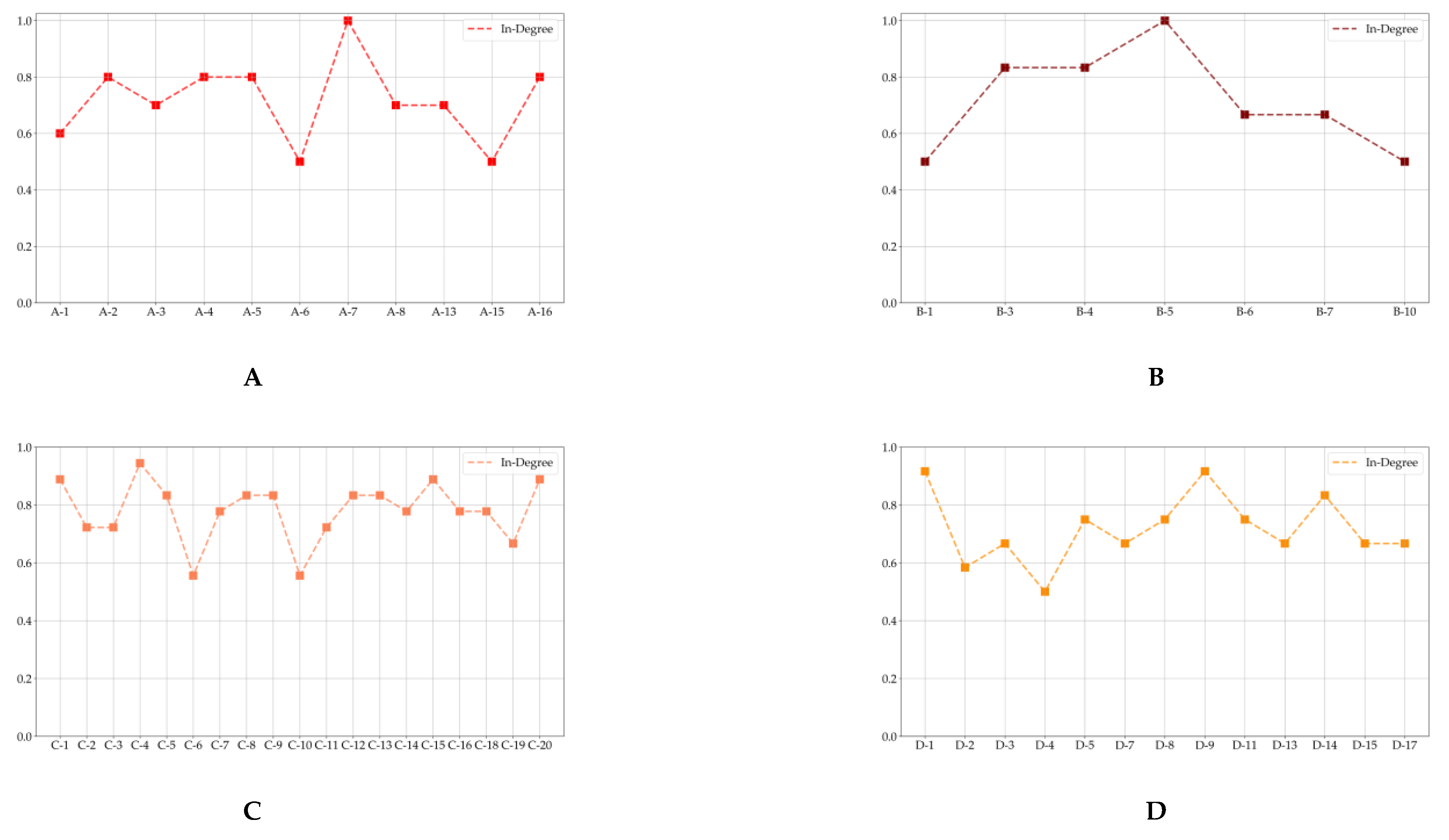
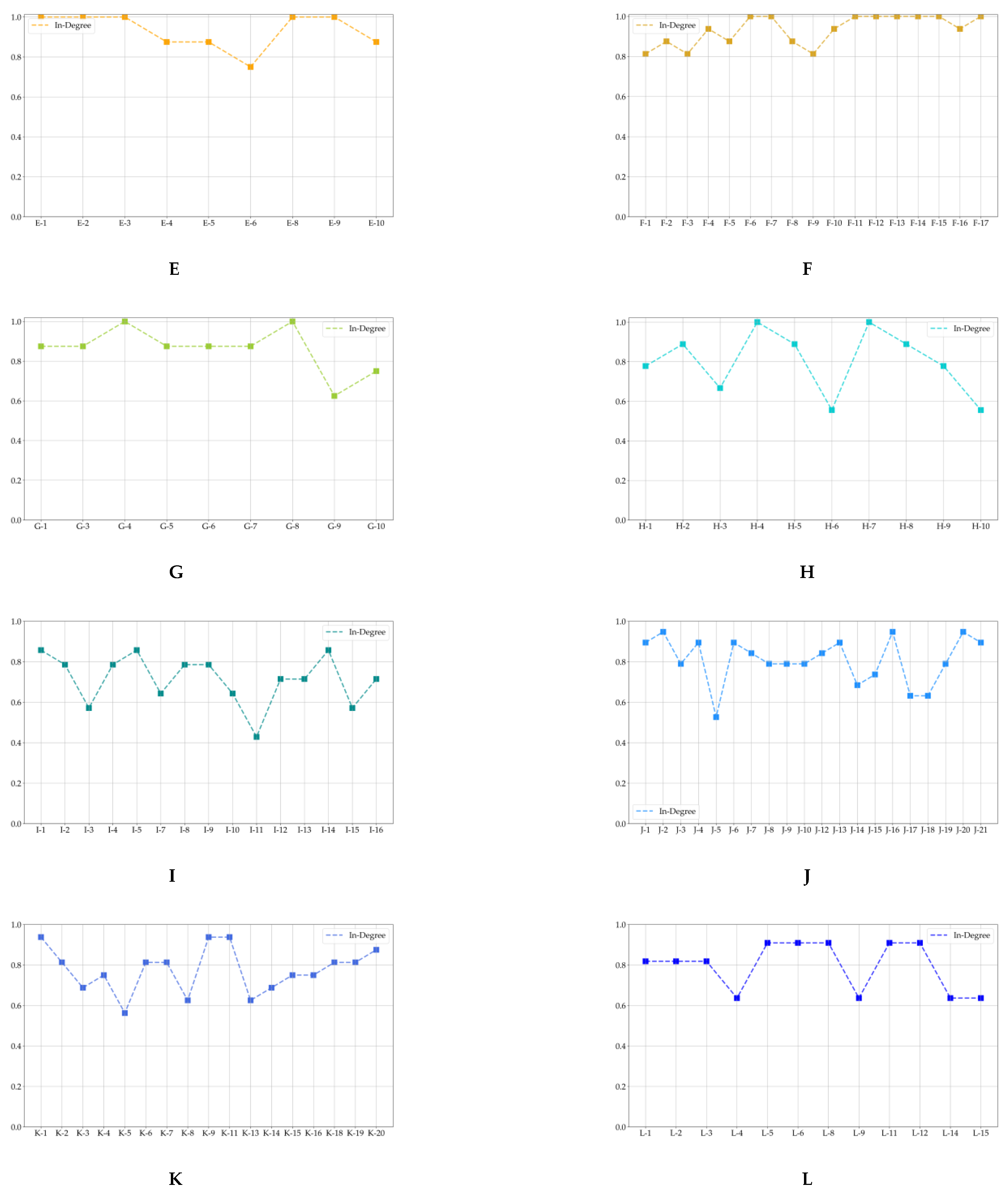
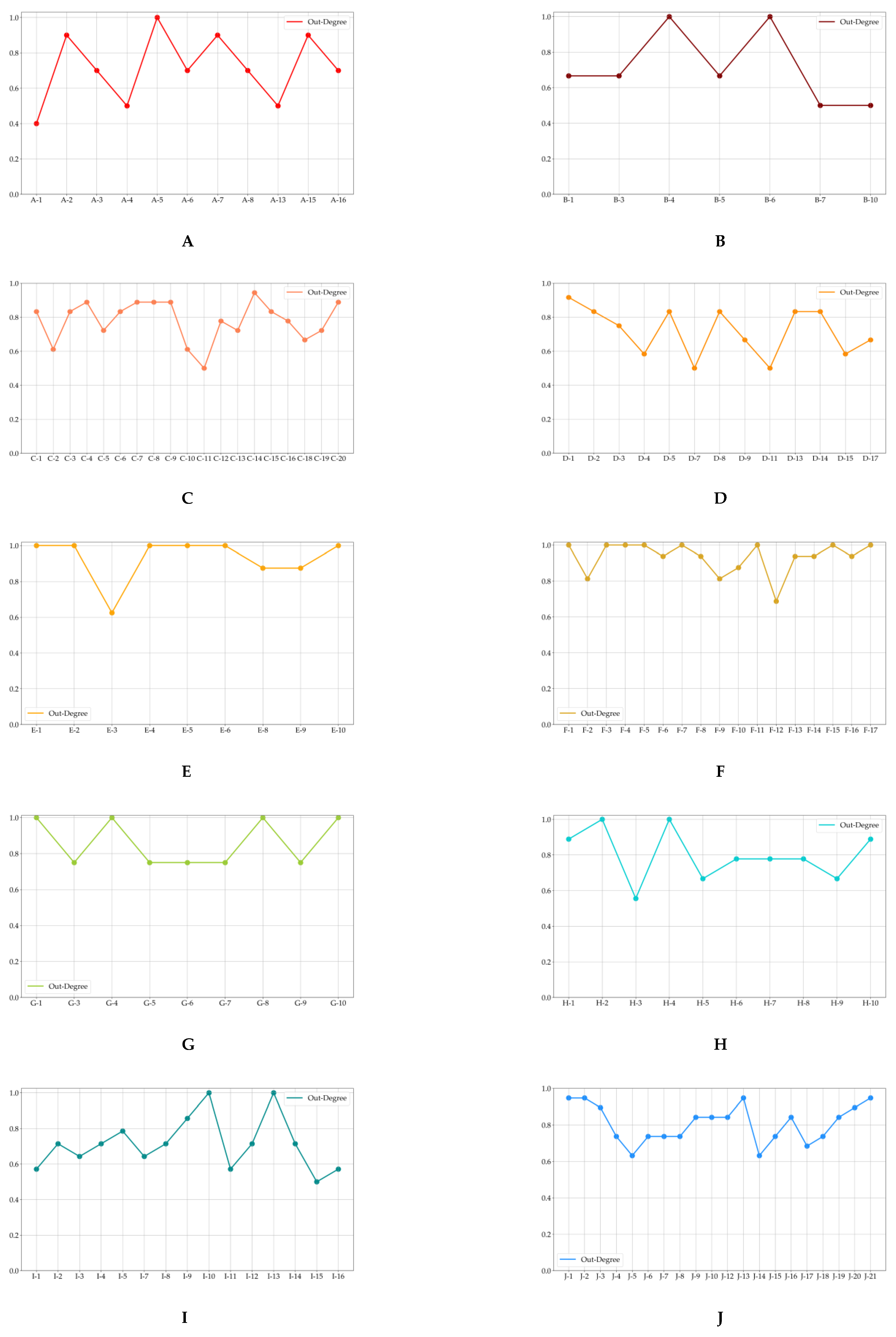
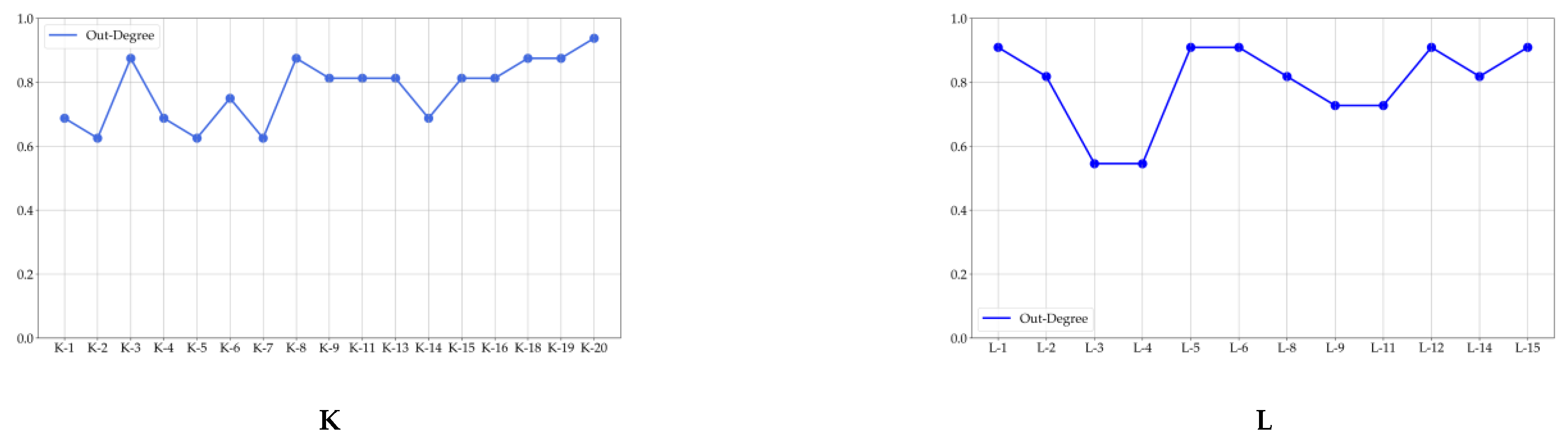
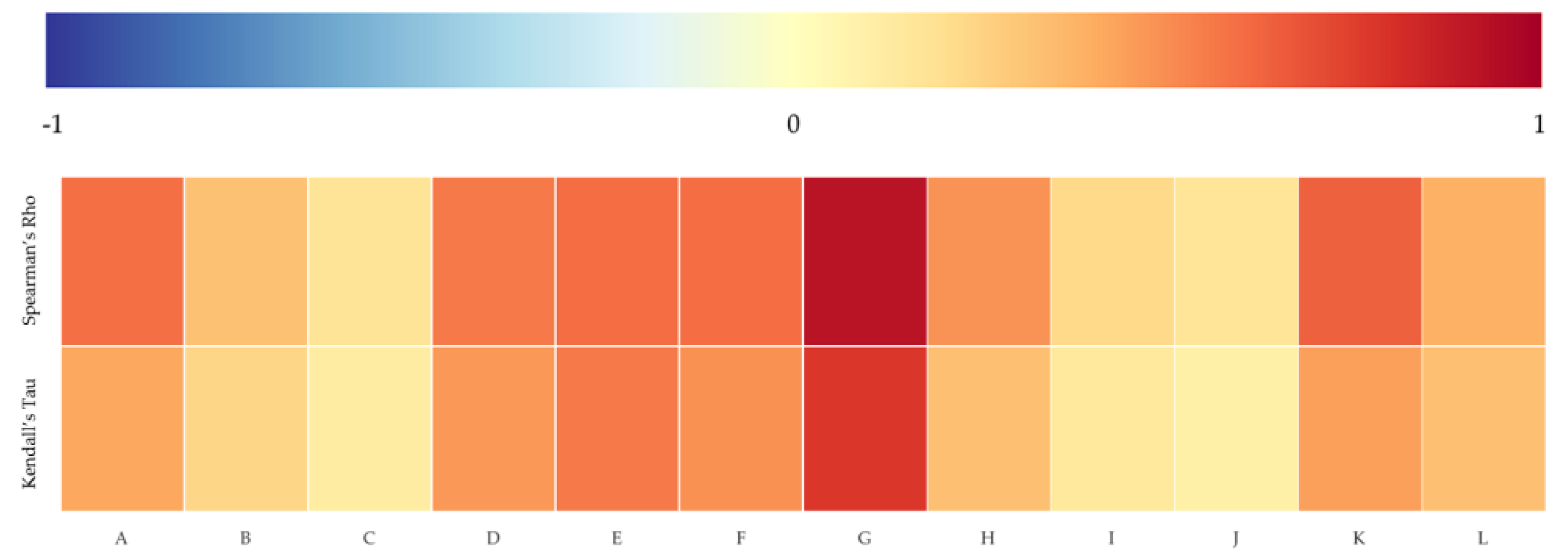
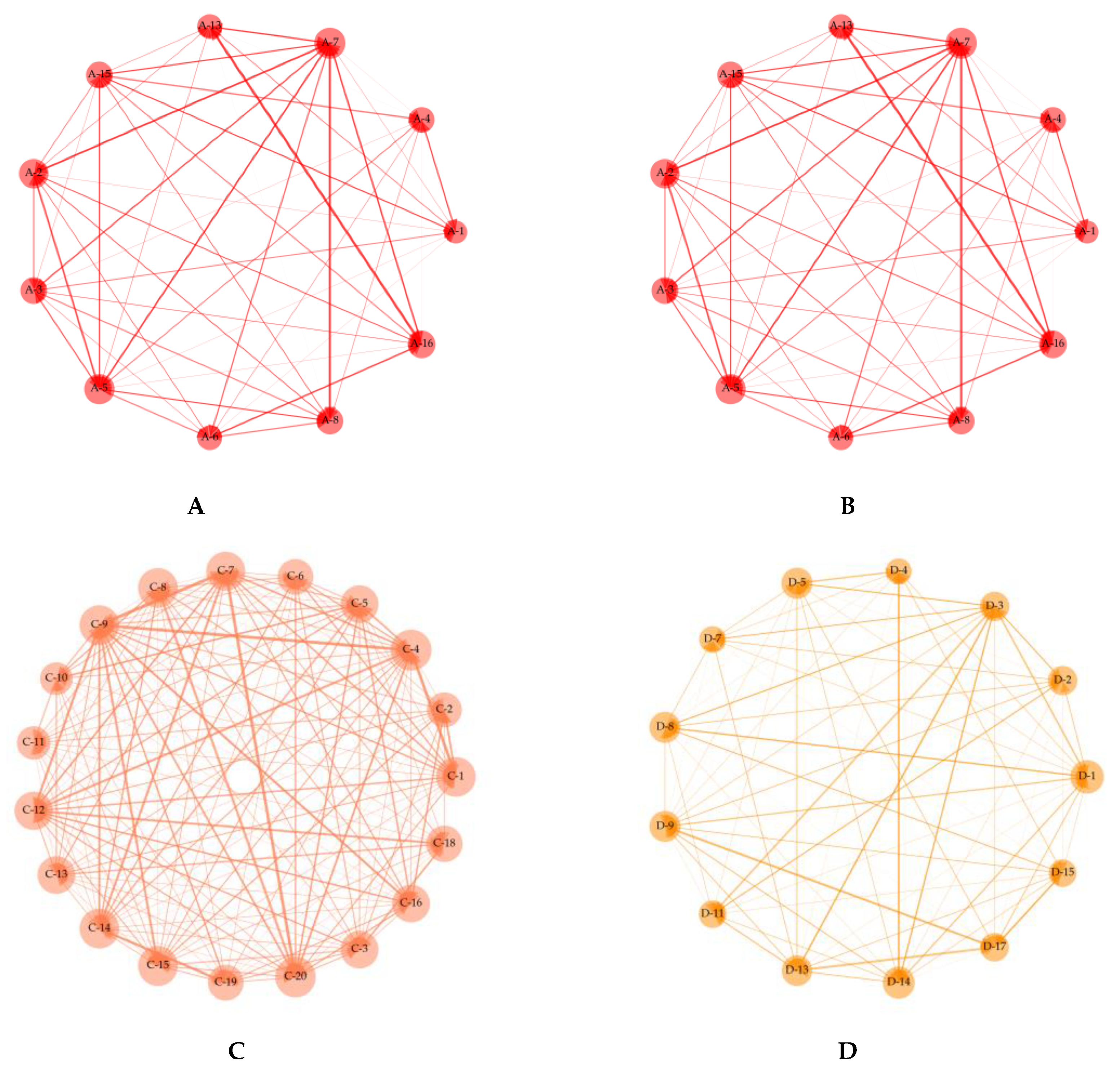
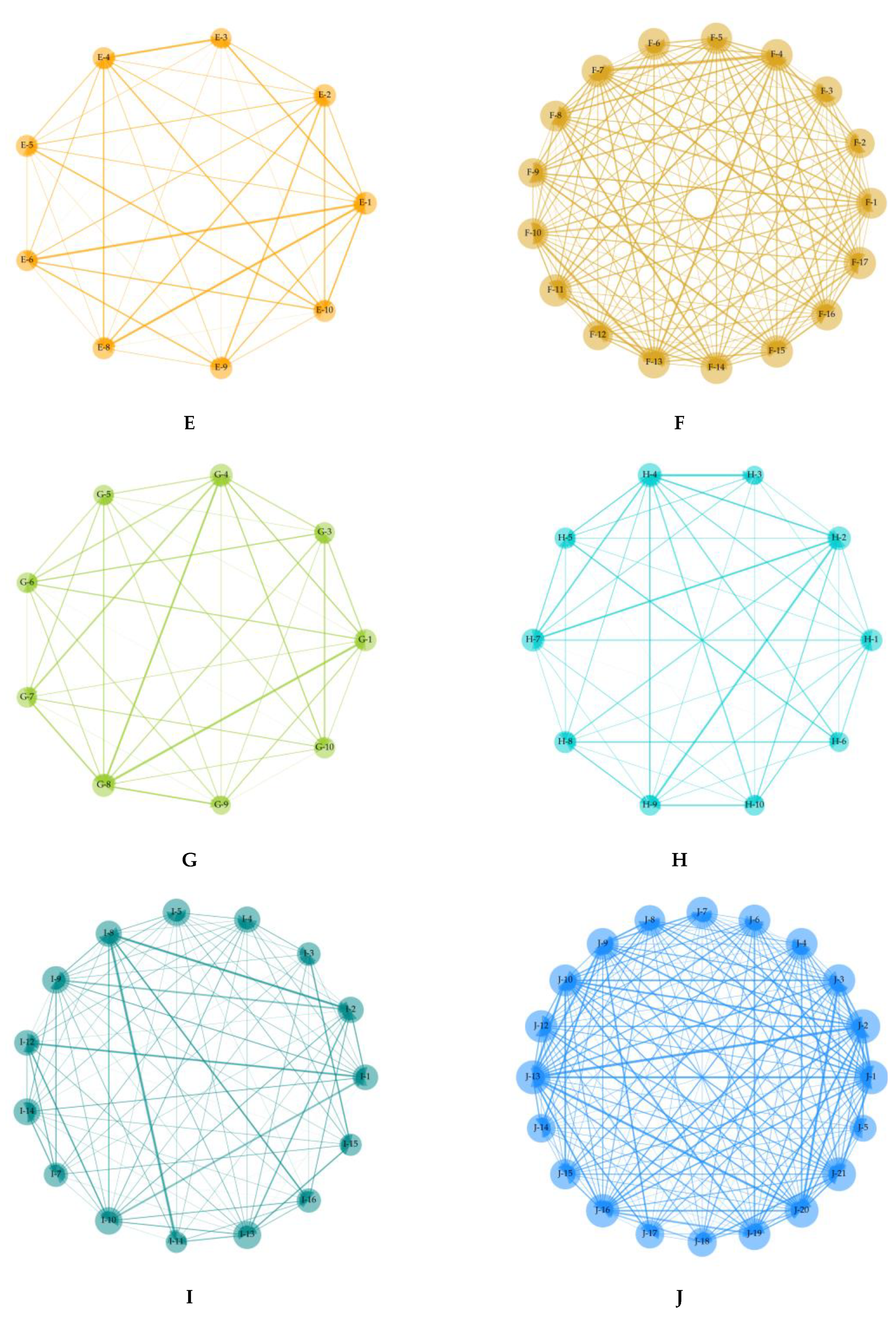
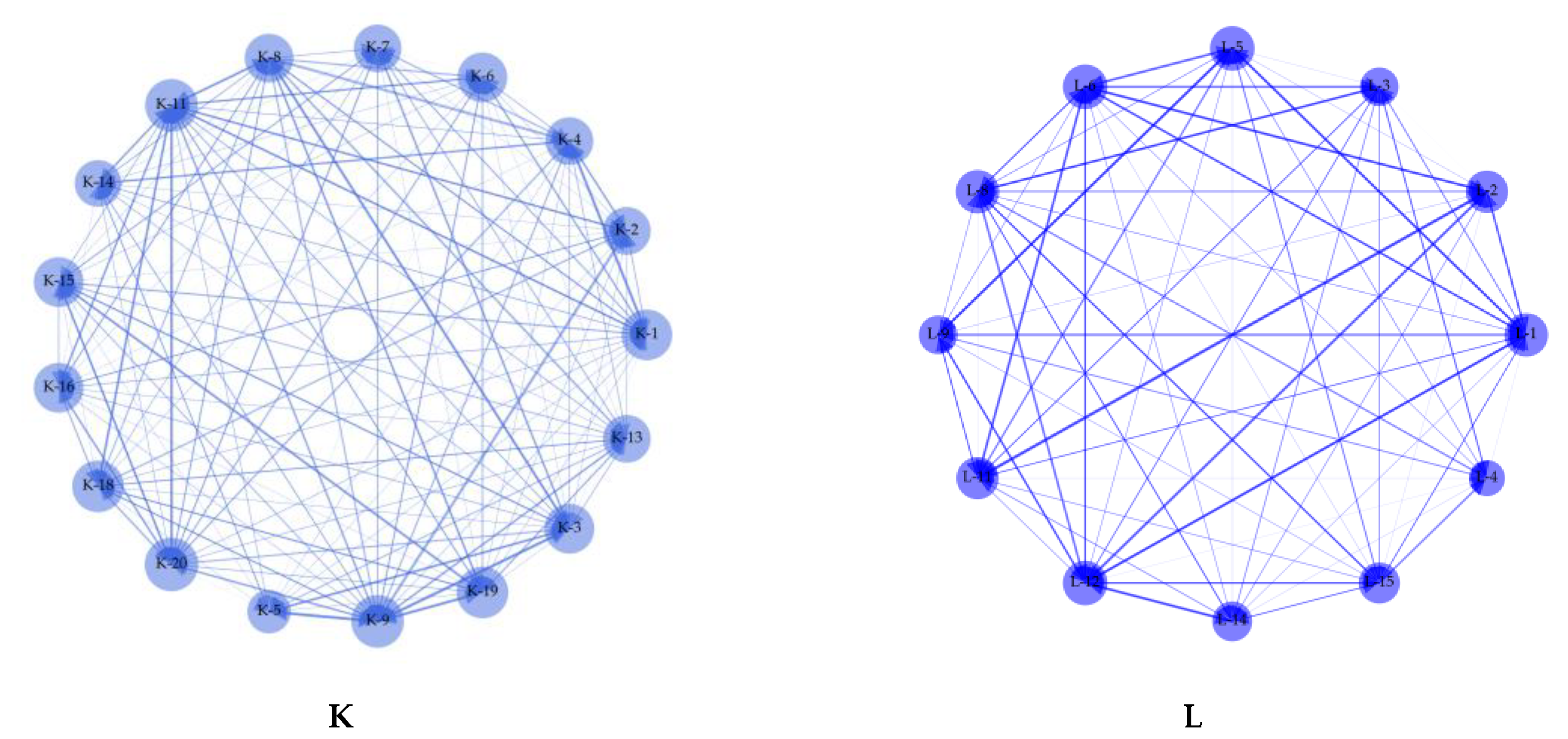
3.3. Developing Politically-Themed Stock Networks
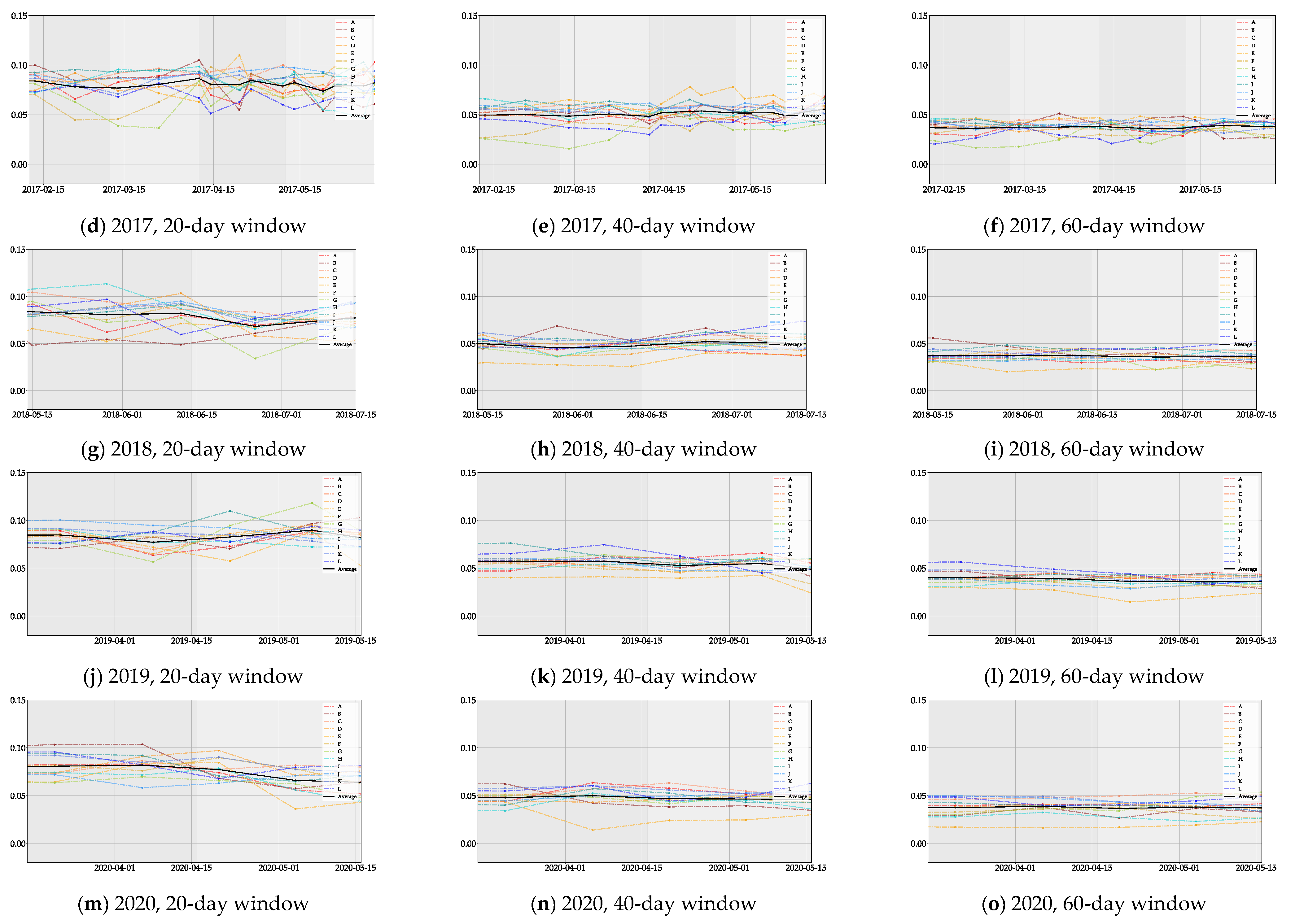
3.4. Network Dynamics Before and after Political Events
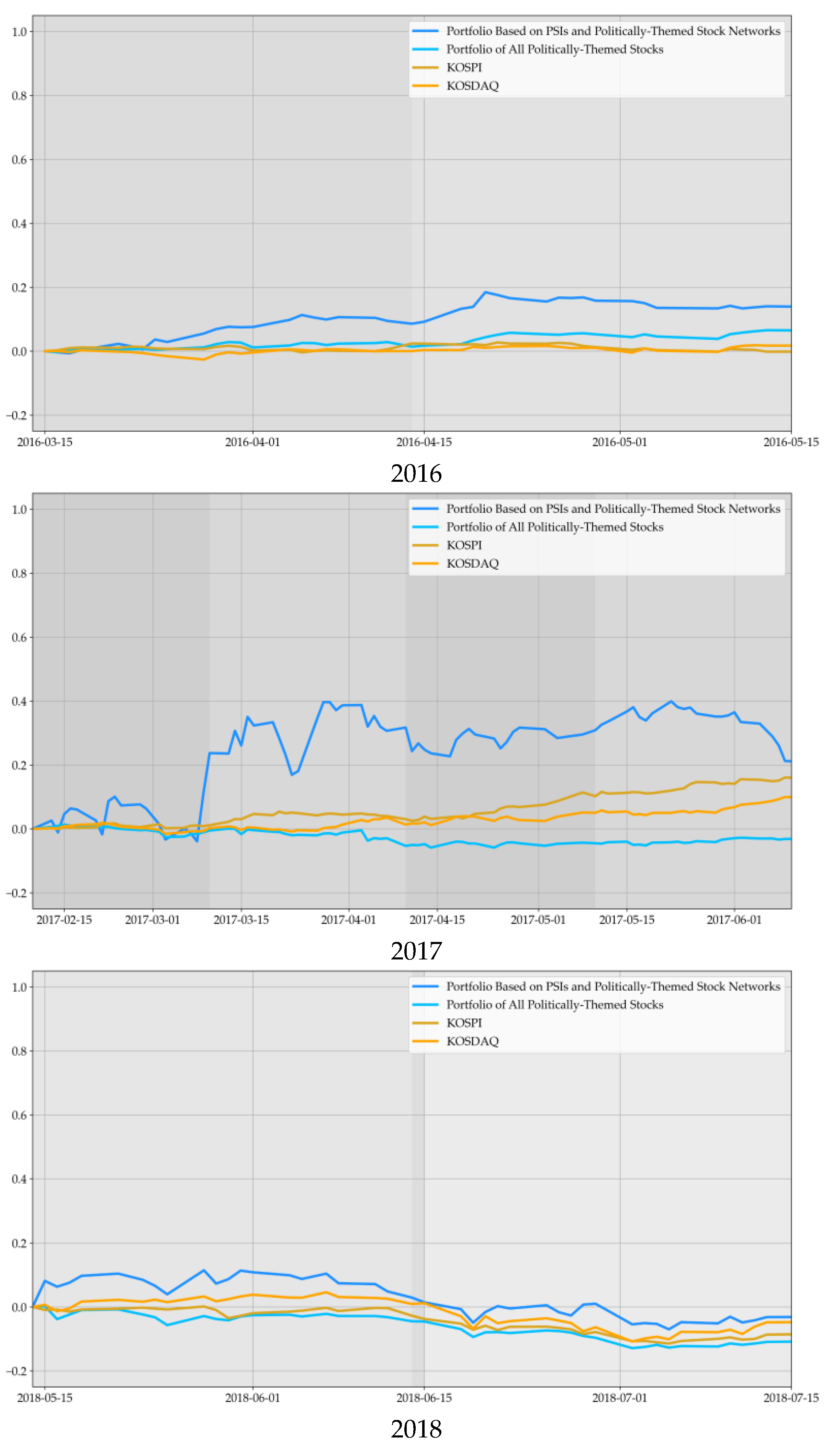
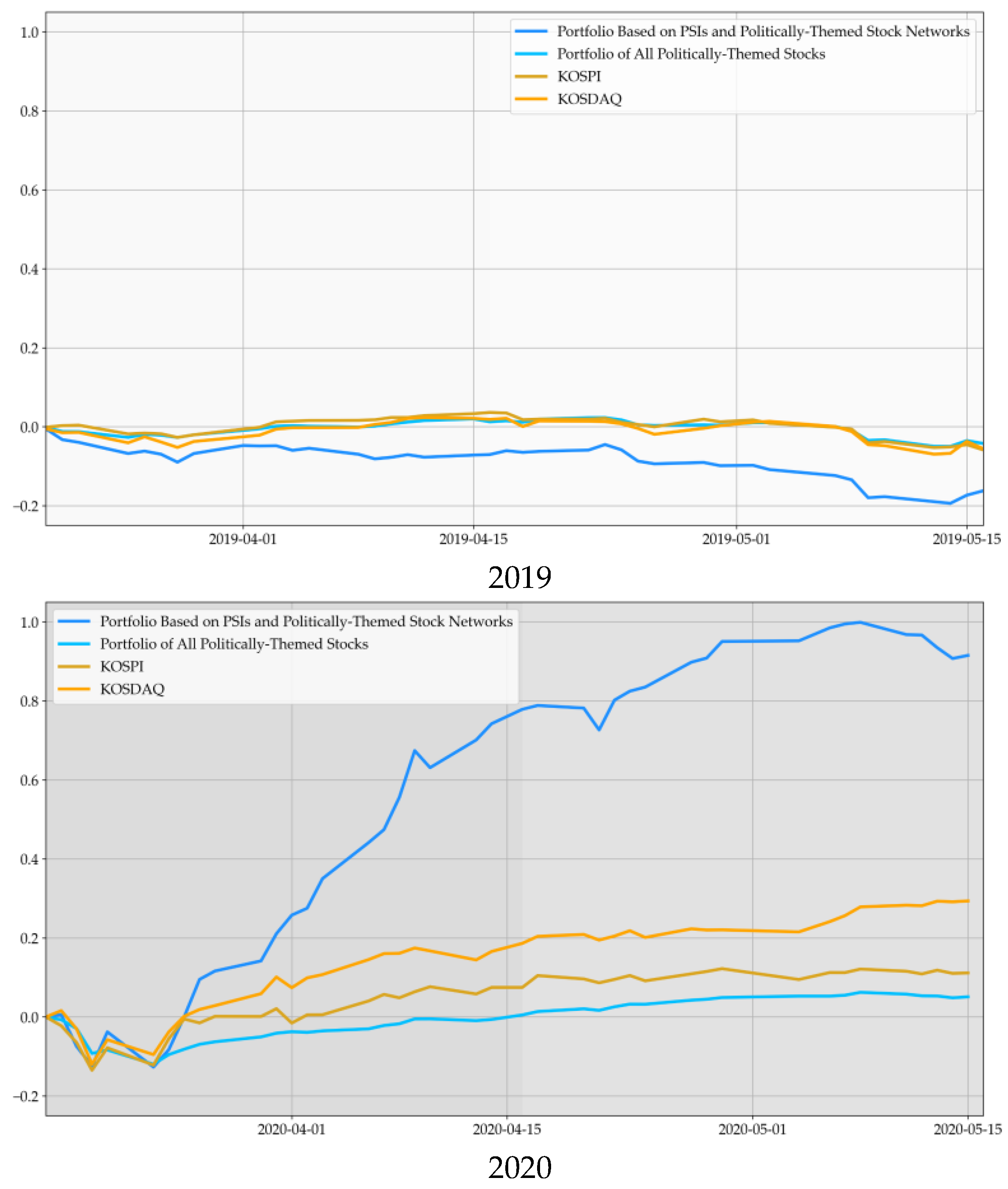
3.5. Investment Strategy Based on PSIs and Politically-Themed Stock Networks
- Step 1:
- Check the daily ROC of the PSI and pick the largest increasing PSI.
- Step 2:
- Select the politically-themed stock networks of the politician whose PSI are selected in the first stage.
- Step 3:
- Optimize the portfolio with the stocks in the selected politically-themed stock networks.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Candidates | Mean (%) | Std. Dev (%) | Min (%) | Max (%) | Q1 (%) | Median (%) | Q3 (%) | Skewness | Kurtosis | W | JB | LM | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A-01 | 7.80 | 3.470 | −20.787 | 27.004 | −1.421 | −0.273 | 1.031 | 2.301 | 18.312 | 0.772 *** | 16,204.559 *** | 13.219 ** | −25.063 *** | 3.967 |
| A-02 | −5.55 | 2.668 | −17.453 | 29.779 | −1.217 | −0.156 | 1.002 | 1.875 | 20.710 | 0.835 *** | 20,131.236 *** | 52.659 *** | −34.344 *** | 15.700 *** |
| A-03 | 3.30 | 3.208 | −14.180 | 28.970 | −1.406 | −0.149 | 1.084 | 2.598 | 21.959 | 0.795 *** | 23,144.340 *** | 5.249 | −13.742 *** | 9.822 *** |
| A-04 | −5.91 | 3.817 | −32.798 | 28.843 | −1.902 | −0.182 | 1.383 | 1.256 | 16.455 | 0.827 *** | 12,590.051 *** | 11.554 | −32.275 *** | 4.553 |
| A-05 | 4.11 | 3.377 | −15.031 | 27.071 | −1.750 | −0.194 | 1.313 | 2.413 | 16.083 | 0.831 *** | 12,816.687 *** | 15.880 ** | −33.985 *** | 23.307 *** |
| A-06 | 5.22 | 2.486 | −8.714 | 25.474 | −1.335 | −0.197 | 1.032 | 2.101 | 15.794 | 0.872 *** | 12,139.403 *** | 6.000 | −12.102 *** | 1.323 |
| A-07 | −3.69 | 3.814 | −26.225 | 28.560 | −1.365 | −0.226 | 0.996 | 1.872 | 16.134 | 0.759 *** | 12,467.613 *** | 67.972 *** | −13.163 *** | 31.027 *** |
| A-08 | 1.49 | 3.594 | −24.164 | 27.991 | −1.474 | −0.151 | 1.063 | 0.845 | 15.656 | 0.786 *** | 11,266.064 *** | 49.046 *** | −19.706 *** | 46.191 *** |
| A-09 | −1.00 | 3.766 | −18.430 | 25.701 | −1.953 | −0.105 | 1.621 | 0.396 | 4.393 | 0.944 *** | 903.625 *** | 2.967 | −30.040 *** | 30.401 *** |
| A-10 | −2.19 | 2.330 | −13.054 | 21.419 | −1.318 | −0.144 | 1.054 | 1.409 | 12.899 | 0.900 *** | 7921.117 *** | 51.823 *** | −36.934 *** | 6.551 ** |
| A-11 | −3.53 | 2.138 | −19.056 | 17.697 | −1.188 | −0.137 | 1.015 | 0.419 | 11.996 | 0.910 *** | 6567.775 *** | 4.942 | −25.476 *** | 3.975 |
| A-12 | −1.15 | 2.377 | −12.246 | 12.276 | −1.441 | −0.215 | 1.220 | 0.467 | 3.177 | 0.959 *** | 497.240 *** | 4.094 | −24.952 *** | 0.539 |
| A-13 | −1.11 | 3.726 | −25.055 | 25.375 | −1.469 | −0.174 | 1.306 | 0.161 | 12.625 | 0.827 *** | 7244.397 *** | 12.892 *** | −11.937 *** | 31.798 *** |
| A-14 | −5.19 | 2.454 | −12.040 | 12.829 | −1.485 | −0.085 | 1.235 | 0.518 | 2.701 | 0.967 *** | 379.422 *** | 12.154** | −34.375 *** | 3.761 |
| A-15 | −9.62 | 1.965 | −10.178 | 25.993 | −0.861 | −0.095 | 0.746 | 3.785 | 45.030 | 0.749 *** | 94,777.412 *** | 43.098 *** | −36.279 *** | 11.138 *** |
| A-16 | −1.18 | 3.831 | −17.361 | 27.185 | −1.807 | −0.243 | 1.138 | 2.207 | 13.521 | 0.805 *** | 9194.960 *** | 20.524 *** | −15.659 *** | 21.140 *** |
| B-01 | 1.08 | 3.373 | −28.367 | 25.368 | −1.212 | −0.240 | 0.830 | 2.206 | 21.515 | 0.739 *** | 21,922.672 *** | 2.403 | −17.812 *** | 19.946 *** |
| B-02 | −1.41 | 5.543 | −35.591 | 26.231 | −2.070 | −0.064 | 1.784 | 0.190 | 10.808 | 0.818 *** | 5311.843 *** | 31.042 *** | −16.449 *** | 24.122 *** |
| B-03 | 1.52 | 4.210 | −36.071 | 25.843 | −1.835 | −0.112 | 1.572 | −0.080 | 12.515 | 0.859 *** | 7115.398 *** | 21.088 *** | −17.160 *** | 17.411 *** |
| B-04 | −1.07 | 2.185 | −9.647 | 24.107 | −0.959 | −0.059 | 0.815 | 1.799 | 19.747 | 0.837 *** | 18,308.790 *** | 0.979 | −13.356 *** | 3.399 |
| B-05 | −3.53 | 3.701 | −18.392 | 25.243 | −1.670 | −0.217 | 1.482 | 1.167 | 10.089 | 0.869 *** | 4871.829 *** | 12.785 *** | −32.350 *** | 28.507 *** |
| B-06 | 3.97 | 2.552 | −30.978 | 19.421 | −1.021 | −0.069 | 1.010 | −0.908 | 28.046 | 0.811 *** | 35,893.676 *** | 8.621 | −33.934 *** | 15.433 *** |
| B-07 | 7.18 | 2.976 | −12.206 | 26.534 | −1.613 | −0.043 | 1.270 | 1.896 | 14.062 | 0.879 *** | 9639.999 *** | 24.486 *** | −24.191 *** | 20.188 *** |
| B-08 | −1.49 | 3.237 | −30.703 | 25.917 | −1.364 | −0.184 | 1.229 | 0.280 | 16.671 | 0.836 *** | 12,640.621 *** | 5.655 | −34.332 *** | 7.485 ** |
| B-09 | −8.64 | 2.729 | −15.923 | 25.605 | −1.200 | −0.130 | 1.025 | 1.443 | 16.376 | 0.851 *** | 12,563.078 *** | 9.203 ** | −11.495 *** | 24.084 *** |
| B-10 | −9.82 | 1.616 | −7.974 | 15.490 | −0.711 | −0.046 | 0.692 | 1.176 | 11.936 | 0.893 *** | 6723.759 *** | 47.183 *** | −22.687 *** | 24.704 *** |
| C-01 | 9.53 | 3.111 | −20.753 | 26.729 | −1.127 | −0.125 | 0.870 | 1.925 | 20.795 | 0.761 *** | 20,325.327 *** | 57.728 *** | −14.387 *** | 14.925 *** |
| C-02 | 3.82 | 3.396 | −17.552 | 27.474 | −1.272 | −0.168 | 1.015 | 2.582 | 23.560 | 0.727 *** | 26,442.857 *** | 31.807 *** | −10.705 *** | 3.519 |
| C-03 | −1.58 | 2.703 | −16.440 | 26.031 | −1.083 | −0.208 | 0.853 | 2.713 | 28.390 | 0.752 *** | 37,974.463 *** | 2.433 | −27.099 *** | 64.061 *** |
| C-04 | −9.94 | 1.565 | −10.132 | 18.293 | −0.623 | 0.038 | 0.626 | 2.006 | 30.090 | 0.780 *** | 41,880.919 *** | 85.083 *** | −10.370 *** | 13.817 *** |
| C-05 | 1.42 | 4.138 | −22.418 | 28.033 | −1.913 | −0.125 | 1.436 | 1.348 | 10.559 | 0.855 *** | 5395.664 *** | 8.653 | −30.719 *** | 0.704 |
| C-06 | 1.78 | 2.710 | −21.275 | 16.383 | −1.330 | −0.090 | 1.174 | −0.321 | 10.253 | 0.893 *** | 4792.655 *** | 44.069 *** | −19.982 *** | 6.696** |
| C-07 | 6.14 | 2.254 | −9.081 | 22.361 | −0.945 | −0.049 | 0.830 | 2.086 | 21.003 | 0.828 *** | 20,839.728 *** | 11.567 * | −9.865 *** | 16.537 *** |
| C-08 | 8.21 | 3.331 | −16.212 | 27.745 | −1.487 | −0.115 | 1.069 | 2.032 | 15.731 | 0.823 *** | 11,998.067 *** | 3.649 | −34.585 *** | 6.697** |
| C-09 | 9.54 | 3.450 | −16.718 | 27.182 | −1.375 | −0.149 | 1.190 | 1.466 | 13.311 | 0.844 *** | 8440.814 *** | 36.586 *** | −20.372 *** | 26.299 *** |
| C-10 | −1.78 | 3.349 | −34.865 | 26.626 | −1.305 | −0.128 | 1.051 | 0.145 | 22.116 | 0.788 *** | 22,227.992 *** | 11.849 | −21.223 *** | 5.093 * |
| C-11 | −7.95 | 4.274 | −35.237 | 27.190 | −1.836 | −0.273 | 1.454 | 1.205 | 15.230 | 0.808 *** | 10,802.502 *** | 4.836 | −13.864 *** | 8.709 ** |
| C-12 | 1.65 | 3.362 | −23.065 | 26.314 | −1.152 | −0.111 | 0.908 | 2.267 | 24.303 | 0.696 *** | 27,778.975 *** | 91.639 *** | −12.001 *** | 33.674 *** |
| C-13 | 7.6 | 3.217 | −34.749 | 27.026 | −1.437 | −0.128 | 1.201 | −0.102 | 20.269 | 0.840 *** | 18,668.992 *** | 134.787 *** | −17.429 *** | 9.457 *** |
| C-14 | −6.16 | 1.830 | −9.118 | 11.841 | −0.927 | −0.092 | 0.749 | 1.093 | 7.310 | 0.898 *** | 2643.939 *** | 18.650 *** | −31.728 *** | 0.865 |
| C-15 | 2.30 | 3.111 | −14.229 | 28.364 | −1.321 | −0.163 | 1.096 | 3.144 | 25.279 | 0.754 *** | 30,845.634 *** | 7.469 | −11.609 *** | 2.673 |
| C-16 | −1.54 | 1.600 | −14.272 | 12.428 | −0.688 | −0.078 | 0.630 | 0.439 | 13.711 | 0.854 *** | 8574.415 *** | 12.170 * | −37.920 *** | 13.444 *** |
| C-17 | 6.90 | 3.112 | −14.170 | 27.238 | −1.406 | −0.130 | 1.112 | 2.222 | 19.833 | 0.825 *** | 18,774.823 *** | 3.609 | −21.055 *** | 2.559 |
| C-18 | 2.12 | 3.330 | −16.444 | 26.193 | −1.591 | −0.148 | 1.550 | 0.819 | 9.064 | 0.902 *** | 3852.926 *** | 7.347 | −24.656 *** | 5.048* |
| C-19 | 6.51 | 1.512 | −10.015 | 6.066 | −0.785 | 0.027 | 0.763 | −0.216 | 3.445 | 0.962 *** | 546.366 *** | 10.864* | −32.629 *** | 11.131 *** |
| C-20 | 4.17 | 3.031 | −12.961 | 26.511 | −1.345 | −0.113 | 0.977 | 2.800 | 22.170 | 0.775 *** | 23,767.101 *** | 6.139 | −35.932 *** | 8.532 ** |
| D-01 | 2.03 | 3.901 | −37.401 | 26.118 | −1.394 | −0.208 | 1.009 | 0.130 | 19.133 | 0.774 *** | 16,634.326 *** | 9.221 | −21.317 *** | 9.172 ** |
| D-02 | −6.99 | 2.891 | −36.989 | 26.760 | −1.251 | −0.143 | 1.002 | −0.355 | 39.303 | 0.772 *** | 70,225.141 *** | 44.244 *** | −10.123 *** | 8.122 ** |
| D-03 | −1.09 | 1.097 | −6.594 | 6.330 | −0.519 | −0.008 | 0.474 | 0.116 | 6.644 | 0.904 *** | 2006.068 *** | 14.626** | −13.331 *** | 22.505 *** |
| D-04 | −3.75 | 4.474 | −35.037 | 27.012 | −2.038 | −0.280 | 1.553 | 0.801 | 11.991 | 0.838 *** | 6647.420 *** | 6.717 | −33.319 *** | 2.870 |
| D-05 | −1.27 | 3.225 | −30.377 | 26.179 | −1.269 | −0.117 | 1.032 | 1.017 | 20.424 | 0.804 *** | 19,142.688 *** | 6.960 | −24.761 *** | 28.871 *** |
| D-06 | 5.28 | 2.679 | −11.842 | 26.184 | −1.061 | −0.083 | 0.924 | 1.672 | 14.589 | 0.855 *** | 10,179.765 *** | 56.458 *** | −26.558 *** | 36.793 *** |
| D-07 | −2.26 | 2.777 | −30.993 | 26.258 | −0.990 | −0.144 | 0.677 | 0.286 | 29.566 | 0.769 *** | 39,738.706 *** | 8.056 | −33.922 *** | 21.451 *** |
| D-08 | 5.50 | 2.465 | −14.390 | 26.132 | −1.166 | −0.067 | 0.913 | 1.848 | 17.038 | 0.854 *** | 13,812.732 *** | 8.070 | −33.352 *** | 1.314 |
| D-09 | −2.05 | 4.213 | −29.333 | 25.244 | −1.834 | −0.220 | 1.488 | 0.481 | 10.900 | 0.847 *** | 5438.065 *** | 5.556 | −26.558 *** | 11.502 *** |
| D-10 | 3.01 | 2.365 | −9.081 | 24.074 | −1.211 | −0.186 | 0.880 | 2.568 | 18.818 | 0.834 *** | 17,294.882 *** | 86.078 *** | −12.209 *** | 33.626 *** |
| D-11 | −2.17 | 3.120 | −18.519 | 29.473 | −1.620 | −0.143 | 1.509 | 1.400 | 12.646 | 0.895 *** | 7622.858 *** | 7.337 | −35.180 *** | 7.373 ** |
| D-12 | 3.81 | 3.833 | −14.891 | 26.985 | −1.845 | −0.459 | 1.272 | 2.800 | 16.140 | 0.782 *** | 13,269.830 *** | 6.964 | −11.839 *** | 9.565 *** |
| D-13 | −1.81 | 3.184 | −31.321 | 26.255 | −1.663 | −0.165 | 1.343 | 0.845 | 19.442 | 0.853 *** | 17,303.858 *** | 2.330 | −17.525 *** | 13.720 *** |
| D-14 | 7.01 | 3.538 | −32.955 | 27.001 | −1.521 | −0.118 | 1.243 | 0.874 | 18.598 | 0.811 *** | 15,854.178 *** | 11.293 | −12.440 *** | 2.636 |
| D-15 | −5.58 | 3.640 | −19.020 | 27.464 | −1.480 | −0.265 | 1.092 | 2.311 | 16.977 | 0.784 *** | 14,071.233 *** | 4.346 | −13.191 *** | 1.681 |
| D-16 | 7.74 | 3.668 | −12.792 | 26.526 | −1.895 | −0.314 | 1.353 | 1.511 | 8.788 | 0.889 *** | 3923.967 *** | 7.059 | −18.138 *** | 1.728 |
| D-17 | −8.38 | 1.766 | −12.504 | 11.619 | −0.940 | −0.130 | 0.770 | 0.490 | 6.122 | 0.924 *** | 1744.632 *** | 7.394 | −18.965 *** | 4.804* |
| D-18 | 1.31 | 1.014 | −6.711 | 6.103 | −0.491 | 0.036 | 0.514 | −0.349 | 4.396 | 0.952 *** | 898.522 *** | 20.885 *** | −35.349 *** | 0.286 |
| E-01 | 2.88 | 3.805 | −14.599 | 26.297 | −1.897 | −0.008 | 1.614 | 1.022 | 6.172 | 0.922 *** | 1920.204 *** | 6.248 | −12.061 *** | 28.562 *** |
| E-02 | 6.45 | 2.328 | −21.137 | 12.143 | −1.351 | 0.005 | 1.162 | −0.407 | 7.558 | 0.948 *** | 2623.226 *** | 22.451 *** | −33.628 *** | 4.229 |
| E-03 | 3.82 | 4.092 | −26.616 | 26.400 | −1.575 | −0.030 | 1.268 | 1.596 | 16.037 | 0.762 *** | 12,150.187 *** | 13.478** | −13.065 *** | 4.177 |
| E-04 | 9.79 | 2.890 | −19.247 | 26.220 | −1.130 | 0.040 | 1.045 | 0.412 | 10.907 | 0.887 *** | 5433.862 *** | 17.184** | −12.861 *** | 33.226 *** |
| E-05 | −1.79 | 3.990 | −22.241 | 26.109 | −1.973 | −0.116 | 1.693 | 0.929 | 10.238 | 0.876 *** | 4917.448 *** | 14.335** | −33.884 *** | 17.797 *** |
| E-06 | −2.34 | 4.244 | −29.222 | 26.417 | −1.901 | −0.121 | 1.489 | 1.364 | 11.891 | 0.830 *** | 6762.581 *** | 24.438 *** | −12.076 *** | 36.809 *** |
| E-07 | −7.41 | 3.723 | −15.106 | 26.450 | −1.892 | −0.316 | 1.394 | 1.854 | 11.657 | 0.854 *** | 6800.392 *** | 1.242 | −19.430 *** | 5.024 * |
| E-08 | −1.20 | 4.189 | −25.016 | 26.192 | −1.729 | −0.028 | 1.492 | 0.965 | 10.760 | 0.850 *** | 5428.559 *** | 22.024 *** | −13.620 *** | 8.967 ** |
| E-09 | −3.84 | 3.528 | −19.795 | 26.264 | −1.304 | 0.041 | 1.085 | 1.670 | 15.070 | 0.818 *** | 10,826.834 *** | 7.994 | −17.424 *** | 6.753** |
| E-10 | −4.65 | 1.894 | −12.502 | 15.700 | −0.762 | 0.045 | 0.786 | 0.136 | 11.172 | 0.870 *** | 5672.015 *** | 47.019 *** | −31.348 *** | 39.182 *** |
| F-01 | 3.06 | 3.220 | −29.617 | 22.745 | −1.257 | 0.012 | 1.225 | 0.129 | 15.894 | 0.819 *** | 11,478.698 *** | 18.111 *** | −11.725 *** | 1.031 |
| F-02 | −8.09 | 4.189 | −25.823 | 26.359 | −1.741 | −0.005 | 1.673 | 0.674 | 11.929 | 0.835 *** | 6546.291 *** | 15.344 *** | −32.680 *** | 0.415 |
| F-03 | 1.33 | 3.672 | −18.643 | 26.242 | −1.813 | −0.094 | 1.810 | 0.688 | 6.642 | 0.926 *** | 2088.889 *** | 9.554 | −33.704 *** | 6.008 ** |
| F-04 | −1.27 | 3.189 | −21.000 | 26.278 | −1.304 | −0.038 | 1.105 | 1.034 | 14.475 | 0.835 *** | 9713.357 *** | 31.986 *** | −15.385 *** | 42.358 *** |
| F-05 | 2.10 | 3.218 | −16.666 | 26.457 | −1.429 | −0.062 | 1.181 | 1.780 | 16.560 | 0.831 *** | 13,037.781 *** | 33.974 *** | −12.295 *** | 9.246 *** |
| F-06 | 3.77 | 4.197 | −23.820 | 26.333 | −1.862 | −0.027 | 1.673 | 0.644 | 9.085 | 0.880 *** | 3823.764 *** | 12.930* | −33.231 *** | 0.531 |
| F-07 | 6.28 | 3.608 | −23.129 | 26.241 | −1.339 | −0.062 | 1.280 | 1.757 | 18.924 | 0.787 *** | 16,835.769 *** | 11.497 *** | −17.698 *** | 3.663 |
| F-08 | −1.31 | 4.064 | −35.929 | 26.120 | −1.824 | −0.069 | 1.545 | 0.655 | 14.288 | 0.840 *** | 9351.655 *** | 32.411 *** | −31.781 *** | 4.442 |
| F-09 | −1.17 | 3.623 | −24.113 | 26.179 | −1.527 | −0.041 | 1.325 | 0.750 | 12.540 | 0.842 *** | 7245.007 *** | 3.477 | −36.828 *** | 5.378* |
| F-10 | 6.89 | 3.841 | −35.558 | 26.224 | −1.412 | −0.017 | 1.148 | 1.048 | 21.981 | 0.755 *** | 22,155.445 *** | 27.797 *** | −20.531 *** | 16.403 *** |
| F-11 | 2.23 | 3.370 | −20.350 | 26.290 | −1.481 | 0.041 | 1.423 | 0.932 | 12.630 | 0.874 *** | 7404.776 *** | 22.033 *** | −31.001 *** | 3.784 |
| F-12 | 1.05 | 2.629 | −16.112 | 25.808 | −1.249 | 0.051 | 1.145 | 1.268 | 15.872 | 0.868 *** | 11,738.897 *** | 1.687 | −33.625 *** | 2.562 |
| F-13 | 4.94 | 3.716 | −15.041 | 26.191 | −1.493 | −0.072 | 1.376 | 1.526 | 11.640 | 0.848 *** | 6579.876 *** | 36.047 *** | −14.147 *** | 26.591 *** |
| F-14 | −2.50 | 3.114 | −26.721 | 21.150 | −1.315 | −0.001 | 1.257 | −0.429 | 16.066 | 0.841 *** | 11,759.776 *** | 52.564 *** | −16.396 *** | 17.000 *** |
| F-15 | 7.44 | 4.421 | −34.481 | 26.310 | −1.954 | −0.070 | 1.692 | 1.049 | 12.675 | 0.839 *** | 7498.967 *** | 2.483 | −31.225 *** | 1.604 |
| F-16 | 1.16 | 3.067 | −26.841 | 26.340 | −1.137 | 0.079 | 0.866 | 1.477 | 28.730 | 0.729 *** | 37,908.277 *** | 17.600 *** | −11.476 *** | 4.082 |
| F-17 | −1.36 | 2.929 | −15.343 | 19.410 | −1.316 | −0.075 | 1.257 | 0.340 | 6.477 | 0.911 *** | 1924.913 *** | 14.506 ** | −30.979 *** | 26.173 *** |
| G-01 | 8.48 | 4.353 | −34.607 | 27.240 | −1.896 | −0.319 | 1.457 | 0.820 | 15.208 | 0.815 *** | 10628.920 *** | 3.686 | −31.566 *** | 13.029 *** |
| G-02 | 6.45 | 3.132 | −29.513 | 24.885 | −1.254 | −0.268 | 1.049 | 0.669 | 23.551 | 0.772 *** | 25,283.544 *** | 11.570 ** | −12.120 *** | 7.194 ** |
| G-03 | −2.13 | 4.173 | −34.452 | 27.415 | −1.635 | −0.198 | 1.155 | 0.755 | 17.326 | 0.782 *** | 13,741.711 *** | 20.899 *** | −12.797 *** | 27.935 *** |
| G-04 | 4.83 | 4.379 | −35.463 | 26.563 | −2.037 | −0.266 | 1.642 | 0.178 | 13.214 | 0.845 *** | 7937.386 *** | 131.945 *** | −14.463 *** | 23.138 *** |
| G-05 | 6.85 | 4.221 | −34.993 | 26.490 | −1.836 | −0.181 | 1.549 | 0.492 | 13.293 | 0.841 *** | 8070.649 *** | 11.632 | −33.966 *** | 4.820 * |
| G-06 | −1.32 | 3.682 | −29.240 | 26.548 | −1.756 | −0.181 | 1.221 | 1.980 | 19.077 | 0.777 *** | 17,251.824 *** | 10.754 | −14.896 *** | 5.412 * |
| G-07 | 6.80 | 3.513 | −16.616 | 26.643 | −1.494 | −0.175 | 1.232 | 1.939 | 14.102 | 0.830 *** | 9721.093 *** | 7.208 | −15.522 *** | 4.083 |
| G-08 | 3.86 | 4.717 | −35.805 | 28.496 | −1.766 | −0.276 | 1.336 | 0.424 | 18.071 | 0.741 *** | 14,869.606 *** | 66.045 *** | −13.646 *** | 19.922 *** |
| G-09 | 7.85 | 3.732 | −38.082 | 28.307 | −1.725 | −0.215 | 1.196 | 0.141 | 21.983 | 0.788 *** | 21,962.016 *** | 49.376 *** | −9.753 *** | 10.230 *** |
| G-10 | −5.95 | 3.800 | −33.613 | 27.678 | −1.642 | −0.189 | 1.370 | 0.626 | 15.746 | 0.829 *** | 11,335.453 *** | 29.833 *** | −14.901 *** | 5.778 * |
| G-11 | 2.12 | 2.239 | −18.530 | 25.439 | −0.876 | −0.092 | 0.636 | 2.737 | 34.196 | 0.723 *** | 54,514.188 *** | 61.706 *** | −30.283 *** | 46.037 *** |
| G-12 | 7.71 | 1.973 | −11.736 | 21.136 | −0.887 | −0.097 | 0.740 | 1.867 | 20.468 | 0.839 *** | 19,673.065 *** | 9.448 * | −19.788 *** | 1.735 |
| G-13 | 8.42 | 2.161 | −12.719 | 20.362 | −0.917 | −0.070 | 0.718 | 2.331 | 22.986 | 0.806 *** | 25,002.236 *** | 38.430 *** | −33.532 *** | 45.435 *** |
| G-14 | 4.60 | 3.175 | −19.835 | 28.252 | −1.501 | −0.090 | 1.157 | 0.978 | 14.133 | 0.866 *** | 9247.918 *** | 6.620 | −19.644 *** | 3.660 |
| G-15 | −1.32 | 2.485 | −17.074 | 25.880 | −1.090 | −0.112 | 0.874 | 1.065 | 18.395 | 0.827 *** | 15,581.134 *** | 4.839 | −12.711 *** | 0.441 |
| H-01 | 9.89 | 3.129 | −17.551 | 26.404 | −1.415 | −0.213 | 1.024 | 2.086 | 14.838 | 0.823 *** | 10,797.339 *** | 19.420 ** | −31.925 *** | 13.076 *** |
| H-02 | 1.95 | 3.527 | −36.557 | 27.629 | −0.889 | −0.068 | 0.732 | 1.216 | 30.366 | 0.655 *** | 42,174.908 *** | 14.998 ** | −13.175 *** | 41.835 *** |
| H-03 | −1.64 | 2.598 | −14.843 | 25.573 | −1.260 | −0.144 | 0.978 | 2.592 | 26.724 | 0.794 *** | 33,681.340 *** | 73.141 *** | −17.645 *** | 39.120 *** |
| H-04 | −2.58 | 2.966 | −13.915 | 26.115 | −1.144 | −0.109 | 0.923 | 2.468 | 19.537 | 0.779 *** | 18,455.896 *** | 13.160 | −25.689 *** | 13.666 *** |
| H-05 | −8.81 | 4.605 | −35.224 | 26.679 | −1.984 | −0.243 | 1.719 | 0.170 | 12.689 | 0.841 *** | 7318.666 *** | 6.126 | −32.865 *** | 0.080 |
| H-06 | 2.98 | 3.852 | −14.686 | 26.599 | −1.959 | −0.249 | 1.587 | 1.130 | 6.756 | 0.917 *** | 2305.123 *** | 32.235 *** | −11.669 *** | 5.109 * |
| H-07 | −1.06 | 4.302 | −29.142 | 27.798 | −1.463 | −0.155 | 1.019 | 1.700 | 16.010 | 0.751 *** | 12,172.832 *** | 20.779 *** | −11.012 *** | 6.447 ** |
| H-08 | 7.18 | 2.656 | −13.958 | 26.870 | −1.220 | −0.121 | 1.037 | 2.216 | 24.134 | 0.829 *** | 27,364.080 *** | 3.773 | −16.275 *** | 0.593 |
| H-09 | −2.33 | 2.239 | −20.620 | 21.711 | −0.886 | 0.008 | 0.748 | 0.816 | 20.535 | 0.809 *** | 19,281.080 *** | 54.392 *** | −26.012 *** | 11.528 *** |
| H-10 | 7.84 | 2.580 | −14.548 | 22.657 | −1.259 | −0.094 | 1.214 | 0.994 | 10.212 | 0.909 *** | 4916.211 *** | 4.808 | −18.166 *** | 21.983 *** |
| I-01 | −1.35 | 2.803 | −18.463 | 25.475 | −1.167 | −0.185 | 0.953 | 1.789 | 19.678 | 0.802 *** | 18,179.682 *** | 131.776 *** | −18.146 *** | 15.403 *** |
| I-02 | −2.14 | 2.280 | −12.802 | 12.771 | −1.201 | −0.182 | 0.974 | 0.635 | 4.674 | 0.930 *** | 1064.612 *** | 7.036 | −13.641 *** | 32.277 *** |
| I-03 | 1.02 | 4.324 | −38.177 | 28.147 | −1.813 | −0.259 | 1.211 | 0.912 | 17.259 | 0.783 *** | 13,684.372 *** | 14.151 | −32.771 *** | 8.985** |
| I-04 | −5.18 | 3.041 | −14.596 | 25.183 | −1.468 | −0.160 | 1.157 | 1.765 | 13.891 | 0.863 *** | 9334.891 *** | 15.990** | −13.131 *** | 4.625* |
| I-05 | 1.84 | 2.899 | −17.801 | 28.158 | −1.500 | −0.154 | 1.012 | 2.386 | 19.500 | 0.821 *** | 18,317.492 *** | 3.246 | −18.929 *** | 23.810 *** |
| I-06 | −1.43 | 3.065 | −16.087 | 26.893 | −1.510 | −0.184 | 1.158 | 2.113 | 17.876 | 0.842 *** | 15,335.228 *** | 11.307 | −38.014 *** | 3.282 |
| I-07 | 7.72 | 2.976 | −12.206 | 26.534 | −1.613 | −0.043 | 1.270 | 1.896 | 14.062 | 0.879 *** | 9639.999 *** | 24.486 *** | −24.191 *** | 20.188 *** |
| I-08 | 9.74 | 3.077 | −17.430 | 29.011 | −1.063 | −0.116 | 0.743 | 3.748 | 35.119 | 0.671 *** | 58621.573 *** | 41.746 *** | −11.816 *** | 27.538 *** |
| I-09 | 2.38 | 3.229 | −16.694 | 26.554 | −1.674 | −0.253 | 1.373 | 1.528 | 13.340 | 0.869 *** | 8509.681 *** | 19.996 *** | −17.668 *** | 5.378* |
| I-10 | 4.52 | 2.737 | −11.565 | 27.410 | −1.152 | −0.115 | 0.895 | 3.572 | 31.317 | 0.747 *** | 46,905.279 *** | 3.151 | −11.253 *** | 6.225** |
| I-11 | −1.88 | 3.509 | −18.669 | 27.277 | −1.367 | −0.182 | 0.835 | 2.809 | 21.357 | 0.731 *** | 22,168.525 *** | 41.987 *** | −14.288 *** | 25.685 *** |
| I-12 | −9.82 | 2.395 | −14.019 | 16.462 | −1.254 | −0.064 | 1.081 | 0.603 | 7.228 | 0.913 *** | 2437.803 *** | 1.731 | −35.143 *** | 1.976 |
| I-13 | 2.04 | 2.587 | −15.653 | 26.689 | −1.234 | −0.036 | 1.035 | 1.038 | 16.233 | 0.866 *** | 12,168.214 *** | 3.293 | −11.551 *** | 14.246 *** |
| I-14 | 4.90 | 2.684 | −16.577 | 25.964 | −1.206 | −0.032 | 1.059 | 1.483 | 15.920 | 0.840 *** | 11,915.415 *** | 0.483 *** | −16.632 *** | 6.738 ** |
| I-15 | −2.90 | 4.395 | −29.781 | 30.821 | −1.714 | −0.269 | 1.154 | 2.039 | 15.686 | 0.761 *** | 11,939.073 *** | 13.690 *** | −11.495 *** | 69.411 *** |
| I-16 | 2.72 | 2.334 | −11.065 | 15.154 | −1.292 | −0.146 | 0.926 | 1.097 | 5.347 | 0.927 *** | 1517.554 *** | 8.285 | −32.841 *** | 1.264 |
| J-01 | 7.48 | 3.647 | −20.694 | 26.734 | −1.722 | −0.211 | 1.323 | 2.218 | 15.988 | 0.824 *** | 12,512.961 *** | 81.391 *** | −17.027 *** | 13.867 *** |
| J-02 | 8.34 | 2.865 | −15.643 | 24.722 | −1.097 | −0.113 | 0.872 | 1.556 | 15.137 | 0.790 *** | 10,851.742 *** | 28.211 *** | −15.795 *** | 57.420 *** |
| J-03 | −1.26 | 3.659 | −35.366 | 26.660 | −1.576 | −0.217 | 1.129 | 1.335 | 20.589 | 0.784 *** | 19,586.324 *** | 19.488 *** | −21.345 *** | 20.661 *** |
| J-04 | −1.25 | 3.785 | −24.498 | 26.709 | −1.676 | −0.310 | 1.142 | 1.380 | 13.706 | 0.820 *** | 8881.830 *** | 32.269 *** | −20.390 *** | 2.641 |
| J-05 | 4.21 | 2.842 | −30.144 | 25.488 | −1.384 | −0.122 | 1.238 | −0.043 | 19.746 | 0.867 *** | 17,716.233 *** | 4.210 | −35.345 *** | 3.986 |
| J-06 | −7.12 | 4.177 | −33.530 | 27.162 | −1.764 | −0.277 | 1.526 | 0.980 | 13.960 | 0.829 *** | 9027.748 *** | 19.530 *** | −14.803 *** | 15.601 *** |
| J-07 | 4.06 | 2.723 | −25.422 | 21.992 | −1.401 | −0.183 | 1.152 | 0.571 | 13.884 | 0.879 *** | 8816.387 *** | 40.553 *** | −22.695 *** | 14.411 *** |
| J-08 | 5.75 | 3.557 | −22.377 | 26.068 | −1.452 | −0.116 | 1.246 | 1.067 | 14.715 | 0.823 *** | 10,044.243 *** | 35.216 *** | −15.326 *** | 22.879 *** |
| J-09 | −5.64 | 2.630 | −10.699 | 17.312 | −1.426 | −0.222 | 1.191 | 1.167 | 5.491 | 0.927 *** | 1617.413 *** | 11.337 | −32.212 *** | 0.764 |
| J-10 | −1.30 | 3.735 | −18.323 | 30.183 | −1.632 | −0.275 | 1.199 | 1.557 | 11.783 | 0.846 *** | 6749.851 *** | 9.396 * | −35.194 *** | 14.362 *** |
| J-11 | 1.50 | 2.671 | −13.358 | 26.249 | −1.361 | −0.192 | 1.017 | 1.917 | 14.203 | 0.867 *** | 9835.555 *** | 3.845 | −11.944 *** | 9.406 *** |
| J-12 | 6.34 | 3.274 | −16.405 | 26.251 | −1.660 | −0.210 | 1.229 | 1.823 | 12.650 | 0.862 *** | 7877.156 *** | 27.135 *** | −33.929 *** | 18.146 *** |
| J-13 | −2.25 | 2.837 | −16.124 | 26.212 | −1.196 | −0.093 | 1.023 | 1.362 | 17.055 | 0.833 *** | 13,554.021 *** | 27.317 *** | −12.941 *** | 27.029 *** |
| J-14 | −4.40 | 2.466 | −16.903 | 26.446 | −1.232 | −0.119 | 1.151 | 1.482 | 19.050 | 0.872 *** | 16,890.711 *** | 10.216 | −33.879 *** | 0.636 |
| J-15 | −6.03 | 3.754 | −20.248 | 26.026 | −1.914 | −0.352 | 1.238 | 1.607 | 8.481 | 0.866 *** | 3738.476 *** | 7.931 | −18.291 *** | 1.735 |
| J-16 | −1.41 | 3.856 | −23.884 | 26.984 | −1.726 | −0.237 | 1.456 | 1.405 | 13.598 | 0.834 *** | 8760.501 *** | 11.731 * | −32.140 *** | 3.139 |
| J-17 | −8.42 | 3.057 | −21.275 | 26.007 | −1.608 | −0.167 | 1.351 | 0.360 | 9.486 | 0.913 *** | 4109.702 *** | 2.502 | −30.941 *** | 0.534 |
| J-18 | −3.33 | 3.386 | −15.643 | 28.146 | −1.689 | −0.204 | 1.377 | 1.298 | 11.047 | 0.881 *** | 5850.550 *** | 9.023 | −31.461 *** | 7.991** |
| J-19 | 4.67 | 3.289 | −16.670 | 27.278 | −1.688 | −0.351 | 1.311 | 1.810 | 13.282 | 0.859 *** | 8613.073 *** | 21.878 *** | −12.093 *** | 7.207** |
| J-20 | −5.45 | 3.120 | −22.460 | 17.443 | −1.317 | −0.127 | 1.045 | 0.641 | 8.307 | 0.872 *** | 3207.947 *** | 59.533 *** | −13.868 *** | 70.497 *** |
| J-21 | −1.15 | 2.023 | −13.129 | 13.704 | −1.013 | −0.097 | 0.895 | 0.210 | 6.371 | 0.926 *** | 1850.185 *** | 27.896 *** | −20.997 *** | 14.047 *** |
| K-01 | −4.94 | 3.658 | −33.702 | 23.782 | −1.578 | −0.164 | 1.396 | −0.371 | 15.419 | 0.848 *** | 10,826.059 *** | 6.526 | −14.184 *** | 0.496 |
| K-02 | 1.27 | 3.349 | −14.596 | 26.030 | −1.536 | −0.210 | 1.292 | 2.425 | 18.411 | 0.819 *** | 16,476.020 *** | 3.060 | −14.841 *** | 2.954 |
| K-03 | 4.19 | 3.764 | −27.868 | 28.539 | −1.614 | −0.201 | 1.252 | 2.162 | 19.281 | 0.778 *** | 17,746.703 *** | 10.383* | −16.646 *** | 12.040 *** |
| K-04 | 2.33 | 3.373 | −25.693 | 27.896 | −1.773 | −0.288 | 1.314 | 1.050 | 12.386 | 0.886 *** | 7169.811 *** | 71.574 *** | −32.740 *** | 6.017 ** |
| K-05 | −9.55 | 3.483 | −34.788 | 26.693 | −1.441 | −0.130 | 1.249 | 0.273 | 19.778 | 0.819 *** | 17,786.721 *** | 7.585 | −36.677 *** | 5.915 * |
| K-06 | 7.03 | 3.033 | −29.122 | 25.613 | −1.413 | −0.150 | 1.247 | −0.019 | 16.239 | 0.861 *** | 11,980.402 *** | 25.279 *** | −19.633 *** | 1.473 |
| K-07 | 8.26 | 2.349 | −8.106 | 25.254 | −1.141 | −0.125 | 0.927 | 3.222 | 30.295 | 0.801 *** | 43,605.779 *** | 2.849 | −18.967 *** | 1.641 |
| K-08 | −9.03 | 3.242 | −15.056 | 26.815 | −1.754 | −0.190 | 1.401 | 1.792 | 11.862 | 0.873 *** | 6978.277 *** | 9.227 | −13.369 *** | 5.999 ** |
| K-09 | −8.01 | 2.657 | −16.187 | 25.194 | −1.163 | −0.191 | 0.996 | 2.352 | 25.198 | 0.778 *** | 29,864.990 *** | 10.380 | −19.151 *** | 18.640 *** |
| K-10 | 7.03 | 3.183 | −12.928 | 26.987 | −1.336 | −0.106 | 0.978 | 2.115 | 15.977 | 0.819 *** | 12,414.995 *** | 13.421 ** | −34.775 *** | 10.558 *** |
| K-11 | 2.93 | 2.361 | −14.868 | 26.247 | −1.108 | −0.046 | 0.940 | 1.551 | 20.038 | 0.857 *** | 18,682.820 *** | 4.013 | −12.766 *** | 2.856 |
| K-12 | 2.69 | 2.072 | −13.266 | 11.806 | −0.926 | −0.046 | 0.880 | 0.156 | 6.546 | 0.918 *** | 1949.383 *** | 9.989 * | −13.625 *** | 3.963 |
| K-13 | −5.98 | 2.042 | −11.094 | 16.164 | −0.927 | −0.006 | 0.759 | 1.176 | 11.361 | 0.864 *** | 6115.036 *** | 42.164 *** | −35.814 *** | 2.079 |
| K-14 | 7.96 | 3.500 | −29.094 | 28.686 | −1.503 | −0.167 | 1.051 | 1.613 | 19.497 | 0.777 *** | 17,747.584 *** | 7.036 | −14.927 *** | 0.555 |
| K-15 | 3.45 | 2.825 | −11.172 | 26.385 | −1.420 | −0.226 | 1.083 | 2.336 | 16.530 | 0.837 *** | 13,411.690 *** | 11.081 | −33.278 *** | 1.568 |
| K-16 | 8.16 | 3.038 | −16.617 | 25.885 | −1.373 | −0.162 | 1.016 | 2.535 | 21.352 | 0.780 *** | 21,892.133 *** | 10.306 | −17.140 *** | 0.813 |
| K-17 | −2.50 | 4.159 | −23.225 | 25.225 | −1.982 | −0.368 | 1.691 | 0.749 | 7.014 | 0.896 *** | 2335.692 *** | 36.769 *** | −16.713 *** | 25.573 *** |
| K-18 | 8.46 | 2.199 | −8.483 | 26.292 | −1.178 | −0.149 | 0.862 | 2.583 | 23.235 | 0.845 *** | 25,750.729 *** | 11.590 | −9.829 *** | 3.241 |
| K-19 | −5.14 | 3.512 | −35.613 | 21.430 | −1.363 | −0.097 | 1.047 | −1.397 | 25.052 | 0.788 *** | 28,874.299 *** | 109.555 *** | −10.360 *** | 40.727 *** |
| K-20 | 1.39 | 2.376 | −14.444 | 19.772 | −1.310 | −0.038 | 1.139 | 0.943 | 9.326 | 0.919 *** | 4112.398 *** | 3.299 | −21.947 *** | 2.621 |
| L-01 | −1.29 | 4.804 | −34.134 | 29.581 | −1.798 | −0.253 | 1.268 | 1.562 | 13.355 | 0.765 *** | 8548.411 *** | 1.740 | −13.269 *** | 3.337 |
| L-02 | −6.79 | 4.421 | −30.571 | 27.679 | −1.861 | −0.213 | 1.204 | 1.575 | 13.293 | 0.793 *** | 8479.967 *** | 11.277 | −31.998 *** | 0.768 |
| L-03 | 1.06 | 2.486 | −9.740 | 26.300 | −1.280 | −0.158 | 1.064 | 1.929 | 16.783 | 0.878 *** | 13,477.710 *** | 42.197 *** | −17.545 *** | 11.435 *** |
| L-04 | −8.62 | 2.818 | −26.526 | 26.572 | −1.184 | −0.118 | 1.133 | −0.065 | 25.180 | 0.805 *** | 28,811.198 *** | 5.898 | −22.251 *** | 0.243 |
| L-05 | 8.69 | 3.214 | −19.021 | 26.295 | −1.569 | −0.125 | 1.407 | 1.208 | 10.096 | 0.894 *** | 4895.420 *** | 154.856 *** | −11.770 *** | 10.909 *** |
| L-06 | −6.21 | 4.030 | −31.602 | 29.639 | −1.654 | −0.202 | 1.396 | 1.013 | 14.734 | 0.820 *** | 10,049.810 *** | 9.272 | −34.450 *** | 3.852 |
| L-07 | −2.82 | 2.245 | −10.034 | 11.762 | −1.203 | −0.165 | 1.065 | 0.491 | 2.463 | 0.965 *** | 318.626 *** | 9.282 | −33.138 *** | 3.543 |
| L-08 | 2.03 | 2.846 | −11.274 | 26.496 | −1.470 | −0.162 | 1.092 | 1.435 | 9.721 | 0.908 *** | 4668.026 *** | 4.064 | −19.677 *** | 12.763 *** |
| L-09 | −9.48 | 4.679 | −36.653 | 30.477 | −2.192 | −0.417 | 1.653 | 0.864 | 12.085 | 0.840 *** | 6769.415 *** | 2.035 | −29.535 *** | 1.952 |
| L-10 | −2.43 | 2.147 | −8.446 | 15.641 | −1.163 | −0.134 | 0.880 | 1.001 | 4.967 | 0.935 *** | 1302.217 *** | 7.029 | −33.817 *** | 12.282 *** |
| L-11 | 5.66 | 3.597 | −20.263 | 27.426 | −1.556 | −0.211 | 1.071 | 1.797 | 14.202 | 0.830 *** | 9753.727 *** | 6.046 | −31.274 *** | 5.357* |
| L-12 | 3.77 | 1.693 | −8.312 | 9.326 | −0.989 | −0.069 | 0.778 | 0.519 | 2.713 | 0.963 *** | 382.672 *** | 2.077 *** | −32.609 *** | 30.995 *** |
| L-13 | 1.52 | 2.379 | −12.784 | 16.216 | −1.378 | −0.123 | 1.231 | 0.650 | 4.706 | 0.947 *** | 1081.628 *** | 8.179 | −34.750 *** | 9.345 *** |
| L-14 | −6.24 | 2.507 | −12.918 | 22.254 | −1.090 | −0.048 | 0.944 | 1.263 | 13.868 | 0.856 *** | 9027.632 *** | 8.759 | −17.650 *** | 4.521 |
| L-15 | −1.10 | 3.415 | −26.605 | 26.900 | −1.628 | −0.141 | 1.308 | 1.038 | 16.555 | 0.839 *** | 12,648.013 *** | 0.853 | −14.431 *** | 4.752 * |
| L-16 | 5.88 | 2.085 | −8.557 | 13.335 | −1.105 | −0.057 | 0.914 | 0.624 | 4.288 | 0.946 *** | 905.028 *** | 3.536 | −10.767 *** | 1.844 |
Appendix B
References
- Herron, M.C.; Lavin, J.; Cram, D.; Silver, J. Measurement of Political Effects in the United States Economy: A Study of the 1992 Presidential Election. Econ. Polit. 1999, 11, 51–81. [Google Scholar] [CrossRef]
- Knight, B. Are Policy Platforms Capitalized into Equity Prices? Evidence from the Bush/Gore 2000 Presidential Election. J. Public Econ. 2006, 90, 751–773. [Google Scholar] [CrossRef]
- Levy, T.; Yagil, J. The 2012 US Presidential Election Polls and Stock Returns. J. Bus. Econ. Res. 2015, 5, 66–74. [Google Scholar] [CrossRef]
- Gobran, P.; Bacon, F. Presidential Elections and Industry Stock Returns: A Test of Market Efficiency. Int. J. Bus. Behav. Sci. 2017, 29, 21–31. [Google Scholar]
- Wagner, A.F.; Zeckhauser, R.J.; Ziegler, A. Company Stock Price Reactions to the 2016 Election Shock: Trump, Taxes, and Trade. J. Financ. Econ. 2018, 130, 428–451. [Google Scholar] [CrossRef]
- Financial Services Commission. Results of Countermeasure against Politically-Themed Stocks of 19th Presidential Election; Press Release in the Republic of Korea: Seoul, Korea, 2017. [Google Scholar]
- Financial Supervisory Service. Survey on Unfair Trade in Politically-Themeds of the 19th Presidential Election; Press Release in the Republic of Korea: Seoul, Korea, 2017.
- Nam, G. Politically-Themed Stocks: Characteristics and Investment Risks. KCMI Issue Rep. 2017, 4, 1–13. [Google Scholar]
- Kwak, H.S.; Yeo, E.J. An Event Study on the Politically-Themed Stocks on the 19th Presidential Election in Korea. Korean J. Financ. Manag. 2019, 36, 209–245. [Google Scholar]
- Hughes, H. Crony capitalism and the East Asian currency and financial ‘crises’. J. Public Policy Ideas 1999, 15, 3–9. [Google Scholar]
- Kim, B.K.; Im, H.B. ‘Crony Capitalism’ in South Korea, Thailand and Taiwan: Myth and Reality. J. East Asian Stud. 2001, 1, 5–52. [Google Scholar] [CrossRef]
- Kang, D.C. Crony Capitalism: Corruption and Development in South Korea and the Philippines; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kang, D.C. Transaction costs and crony capitalism in East Asia. Comp. Political Stud. 2003, 35, 439–458. [Google Scholar] [CrossRef]
- Brown, S.J.; Warner, J.B. Using Daily Stock Returns: The Case of Event Studies. J. Financ. Econ. 1985, 14, 3–31. [Google Scholar] [CrossRef]
- Armitage, S. Event study methods and evidence on their performance. J. Econ. Surv. 1995, 9, 25–52. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. LSTM Can Solve Hard Long Time Lag Problems. Adv. Neural. Inform. Process. Syst. 1997, 473–479. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Park, S.M.; Na, C.W.; Choi, M.S.; Lee, D.H.; On, B.W. KNU Korean Sentiment Lexicon: Bi-LSTM-Based Method for Building a Korean Sentiment Lexicon. J. Intell. Inf. Syst. 2018, 24, 219–240. [Google Scholar]
- Song, M.; Park, H.; Shin, K.S. Attention-Based Long Short-Term Memory Network Using Sentiment Lexicon Embedding for Aspect-Level Sentiment Analysis in Korean. Inf. Process. Manag. 2019, 56, 637–653. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econom. J. Econ. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Quigley, L. Statistical Analysis of the Log Returns of Financial Assets. Master’s thesis. Master’s Thesis, University of Limerick, Limerick, Ireland, 2008. [Google Scholar]
- Sheikh, A.Z.; Qiao, H. Non-normality of Market Returns: A Framework for Asset Allocation Decision Making. J. Alter. Investig. 2009, 12, 8–35. [Google Scholar] [CrossRef][Green Version]
- Tsai, C.S.-Y. The Real World Is Not Normal; Morningstar Alternative Investments Observer: Chicago, IL, USA, 2011. [Google Scholar]
- Schinckus, C. Is Econophysics a New Discipline? The Neopositivist Argument. Phys. A Stat. Mech. Appl. 2010, 389, 3814–3821. [Google Scholar] [CrossRef]
- Jovanovic, F.; Schinckus, C. The Emergence of Econophysics: A New Approach in Modern Financial Theory. Hist. Polit. Econ. 2013, 45, 443–474. [Google Scholar] [CrossRef][Green Version]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Transfer Entropy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Marschinski, R.; Kantz, H. Analysing the Information Flow between Financial Time-series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Kwon, O.; Yang, J.S. Information Flow between Composite Stock Index and Individual Stocks. Phys. A Stat. Mech. Appl. 2008, 387, 2851–2856. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. Using Transfer Entropy to Measure Information Flows Between Financial Markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102. [Google Scholar] [CrossRef]
- Sandoval, L. Structure of a Global Network of Financial Companies Based on Transfer Entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Sensoy, A.; Sobaci, C.; Sensoy, S.; Alali, F. Effective Transfer Entropy Approach to Information Flow between Exchange Rates and Stock Markets. Chaos Solitons Fractals 2014, 68, 180–185. [Google Scholar] [CrossRef]
- Bekiros, S.; Nguyen, D.K.; Junior, L.S.; Uddin, G.S. Information Diffusion, Cluster Formation and Entropy-Based Network Dynamics in Equity and Commodity Markets. Eur. J. Oper. Res. 2017, 256, 945–961. [Google Scholar] [CrossRef]
- Lim, K.; Kim, S.; Kim, S.Y. Information Transfer across Intra/Inter-Structure of CDS and Stock Markets. Phys. A 2017, 486, 118–126. [Google Scholar] [CrossRef]
- Jang, S.M.; Yi, E.; Kim, W.C.; Ahn, K. Information Flow between Bitcoin and Other Investment Assets. Entropy 2019, 21, 1116. [Google Scholar] [CrossRef]
- Yue, P.; Cai, Q.; Yan, W.; Zhou, W.X. Information Flow Networks of Chinese Stock Market Sectors. IEEE Access 2020, 8, 13066–13077. [Google Scholar] [CrossRef]
- Yue, P.; Fan, Y.; Batten, J.A.; Zhou, W.X. Information Transfer between Stock Market Sectors: A Comparison between the USA and China. Entropy 2020, 22, 194. [Google Scholar] [CrossRef] [PubMed]
- Doane, D.P. Aesthetic Frequency Classifications. Am. Stat. 1976, 30, 181–183. [Google Scholar]
- Freedman, D.; Diaconis, P. On the Histogram as a Density Estimator: L2 Theory. Z. Wahrscheinlichkeitstheor. Verw. Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Allen, F.; Babus, A. Networks in Finance. In The Network Challenge: Strategy, Profit, and Risk in an Interlinked World, 1st ed.; Kleindorfer, P.R., Wind, Y., Gunther, R.E., Eds.; FT Press: Upper Saddle River, NJ, USA, 2009; p. 367. [Google Scholar]
- Beije, P.R.; Groenewegen, J. A Network Analysis of Markets. J. Econ. Issues 1992, 26, 87–114. [Google Scholar] [CrossRef]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G.R. Network Analysis of a Financial Market Based on Genuine Correlation and Threshold Method. Phys. A Stat. Mech. Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Huang, W.Q.; Zhuang, X.T.; Yao, S. A Network Analysis of the Chinese Stock Market. Phys. A Stat. Mech. Appl. 2009, 388, 2956–2964. [Google Scholar] [CrossRef]
- Roy, R.B.; Sarkar, U.K. Identifying Influential Stock Indices from Global Stock Markets: A Social Network Analysis Approach. Procedia Comput. Sci. 2011, 5, 442–449. [Google Scholar] [CrossRef]
- Liao, H.; Mariani, M.S.; Medo, M.; Zhang, Y.C.; Zhou, M.Y. Ranking in Evolving Complex Networks. Phys. Rep. 2017, 689, 1–54. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Stanford Infolab, Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Kuzubaş, T.U.; Ömercikoğlu, I.; Saltoğlu, B. Network Centrality Measures and Systemic Risk: An Application to the Turkish Financial Crisis. Phys. A Stat. Mech. Appl. 2014, 405, 203–215. [Google Scholar] [CrossRef]
- Yun, T.S.; Jeong, D.; Park, S. “Too Central to Fail” Systemic Risk Measure Using PageRank Algorithm. J. Econ. Behav. Organ. 2019, 162, 251–272. [Google Scholar] [CrossRef]
- Tu, C. Cointegration-Based Financial Networks Study in Chinese Stock Market. Phys. A Stat. Mech. Appl. 2014, 402, 245–254. [Google Scholar] [CrossRef]
- Tang, Y.; Xiong, J.J.; Luo, Y.; Zhang, Y.C. How Do the Global Stock Markets Influence One Another? Evidence from Finance Big Data and Granger Causality Directed Network. Int. J. Electron. Commer. 2019, 23, 85–109. [Google Scholar] [CrossRef]
- Higham, D.J. Google PageRank as Mean Playing Time for Pinball on the Reverse Web. Appl. Math. Lett. 2005, 18, 1359–1362. [Google Scholar] [CrossRef][Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nam, G. Concerns over Political–Themed Stocks Ahead of Korea’s 21st General Election. Cap. Mark. Focus 2020, 2, 1–5. [Google Scholar]
- Kim, W.C.; Lee, Y.; Lee, Y.H. Cost of Asset Allocation in Equity Market: How Much Do Investors Lose Due to Bad Asset Class Design? J. Portf. Manag. 2014, 41, 34–44. [Google Scholar] [CrossRef]
- Sharpe, W.F. Mutual Fund Performance. J. Bus. 1966, 39, 119–138. [Google Scholar] [CrossRef]
- Sharpe, W.F. The Sharpe Ratio. J. Portf. Manag. 1994, 21, 49–58. [Google Scholar] [CrossRef]
- Goedhart, M.; Koller, T.; Wessels, D. Valuation: Measuring and Managing the Value of Companies; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Iyengar, G.; Kang, W. Inverse Conic Programming with Applications. Oper. Res. Lett. 2005, 33, 319–330. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local Information Transfer as a Spatiotemporal Filter for Complex Systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Dashtipour, K.; Gogate, M.; Li, J.; Jiang, F.; Kong, B.; Hussain, A. A hybrid Persian sentiment analysis framework: Integrating dependency grammar based rules and deep neural networks. Neurocomputing 2020, 380, 1–10. [Google Scholar] [CrossRef]
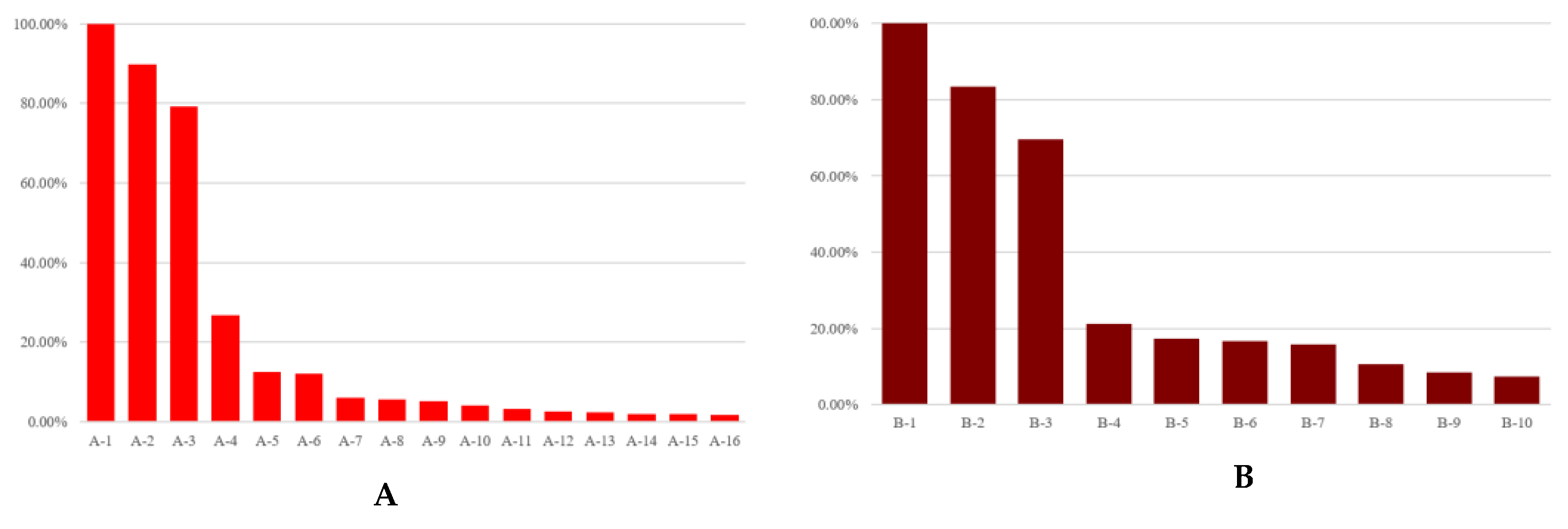
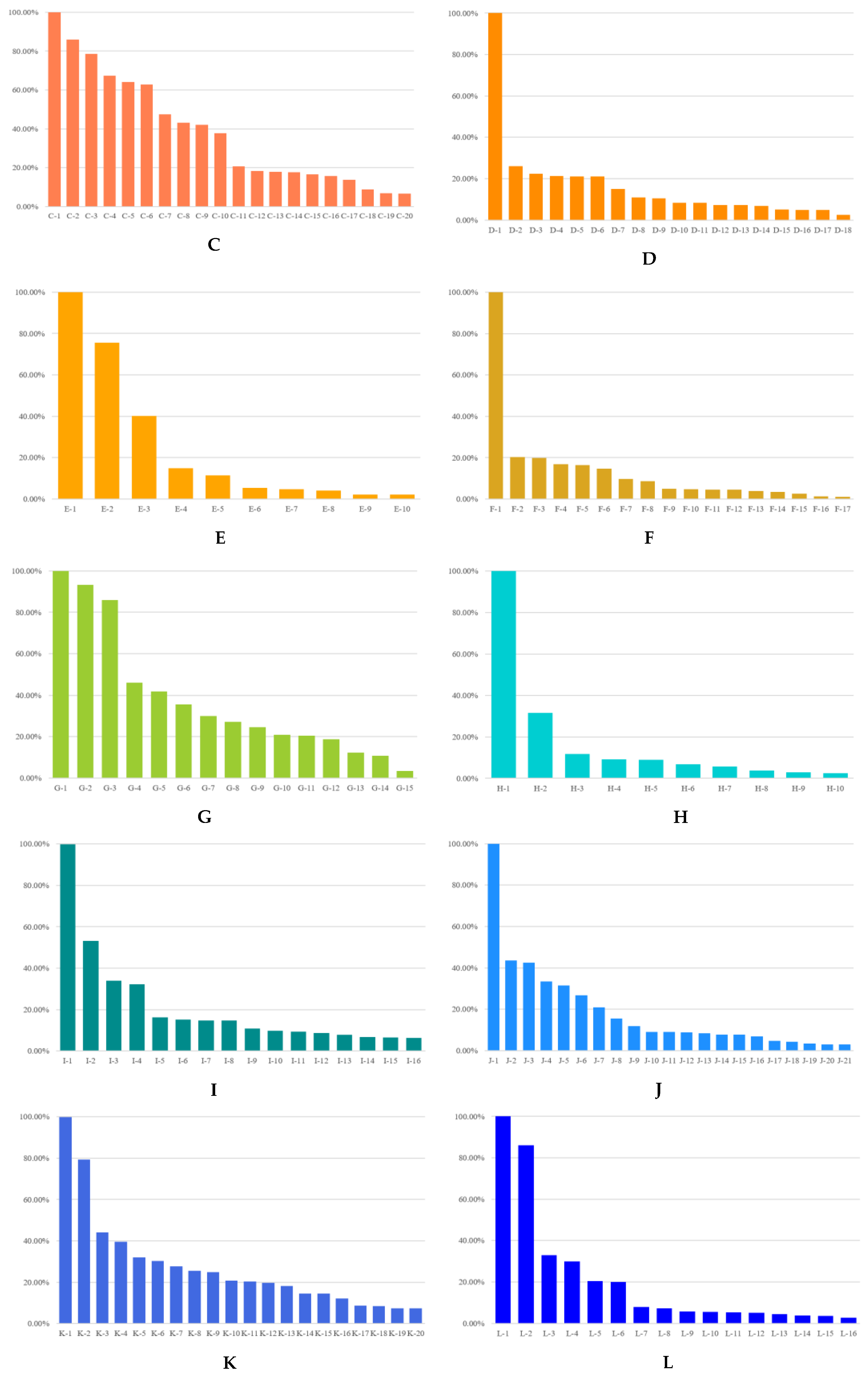
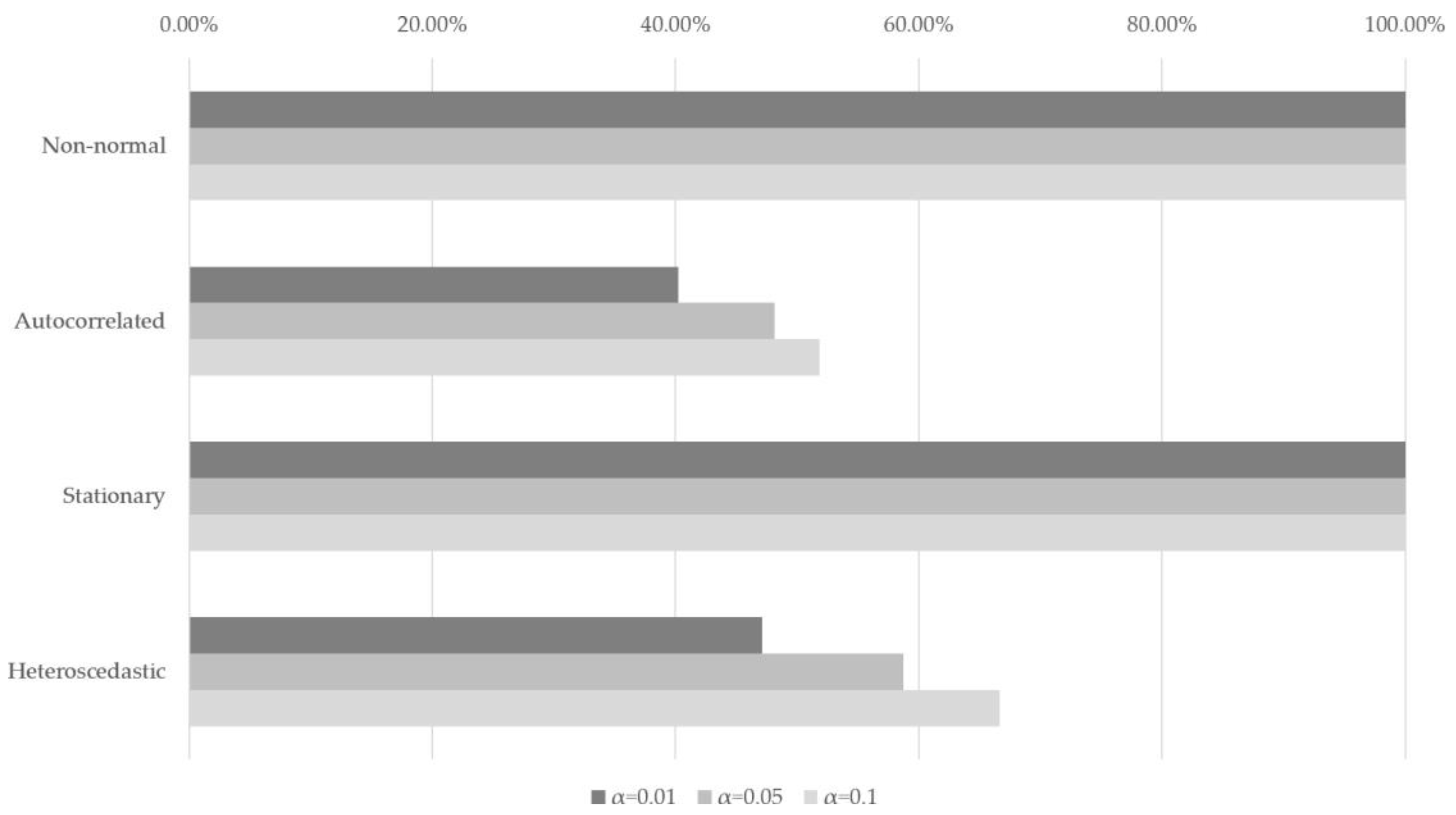
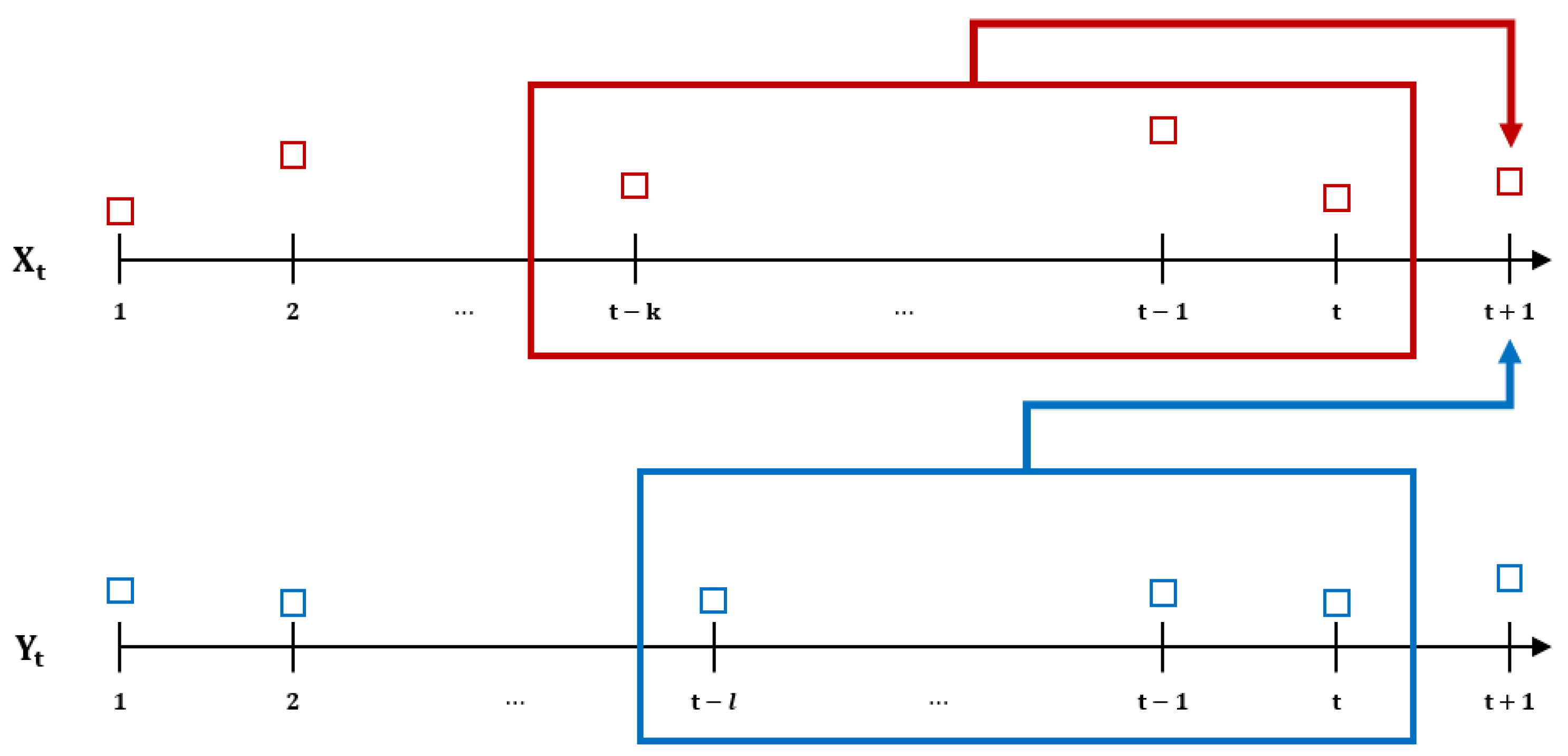


| Date | Description |
|---|---|
| 13 April 2016 | Twentieth Legislative Election |
| 10 March 2017 | Impeachment of the Eighteenth President |
| 9 May 2017 | Nineteenth Presidential Election |
| 13 June 2018 | Seventh Local Election |
| 15 August 2020 | Twenty-First Legislative Election |
| Politician | Political Orientation | Presidential Elected Experience | Presidential Election Experience | Election (Presidential, Legislative, and Local) Experience | Strongly Mentioned as a Presidential Candidate from the Press |
|---|---|---|---|---|---|
| A | Right-Wing | O | O | O | O |
| B | Right-Wing | X | O | O | O |
| C | Right-Wing | X | X | O | O |
| D | Right-Wing | X | X | O | O |
| E | Right-Wing | X | O | O | O |
| F | Right-Wing | X | O | O | O |
| G | Neutral | X | X | X | O |
| H | Left-Wing | X | X | X | O |
| I | Left-Wing | X | X | O | O |
| J | Left-Wing | X | O | O | O |
| K | Left-Wing | X | X | O | O |
| L | Left-Wing | O | O | O | O |
| Politician | Mean (%) | Std. Dev (%) | Min (%) | Max (%) | Q1 (%) | Median (%) | Q3 (%) | Skewness | Kurtosis | W | JB | LM | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.060 | −7.711 | 5.433 | −0.568 | −0.009 | 0.594 | −0.273 | 5.673 | 0.949 *** | 1474.051 *** | 48.168 *** | −12.028 *** | 8.451 ** | |
| B | 1.492 | −8.593 | 6.614 | −0.775 | −0.088 | 0.666 | 0.271 | 3.103 | 0.954 *** | 449.521 *** | 11.023 | −29.848 *** | 18.647 *** | |
| C | 1.130 | −8.508 | 8.121 | −0.590 | −0.045 | 0.526 | 0.318 | 8.517 | 0.918 *** | 3312.044 *** | 66.881 *** | −20.114 *** | 25.244 *** | |
| D | 1.207 | −12.540 | 6.456 | −0.642 | −0.013 | 0.603 | −0.762 | 13.475 | 0.912 *** | 8354.230 *** | 9.883 | −30.803 *** | 5.092 * | |
| E | 1.963 | −15.240 | 9.683 | −0.921 | 0.064 | 0.946 | −0.483 | 6.580 | 0.925 *** | 2007.802 *** | 35.672 *** | −21.668 *** | 6.463 ** | |
| F | 2.012 | −16.188 | 11.173 | −0.804 | 0.105 | 0.964 | −0.939 | 10.883 | 0.872 *** | 5540.561 *** | 9.983 ** | −20.770 *** | 2.226 | |
| G | 1.972 | −26.775 | 10.837 | −0.849 | −0.122 | 0.787 | −2.213 | 35.542 | 0.810 *** | 58,303.427 *** | 14.509 * | −16.300 *** | 7.910 ** | |
| H | 1.070 | −7.491 | 5.728 | −0.618 | −0.027 | 0.575 | 0.123 | 5.194 | 0.942 *** | 1226.414 *** | 4.064 | −21.996 *** | 47.254 *** | |
| I | 1.319 | −6.112 | 9.368 | −0.674 | −0.035 | 0.579 | 0.024 | 3.942 | 0.965 *** | 704.575 *** | 39.647 *** | −21.273 *** | 8.406 ** | |
| J | 1.083 | −6.514 | 5.441 | −0.568 | −0.036 | 0.521 | 0.761 | 7.508 | 0.913 *** | 2664.724 *** | 23.538 *** | −12.017 *** | 55.659 *** | |
| K | 1.507 | −12.600 | 8.581 | −0.758 | −0.006 | 0.649 | 0.018 | 4.254 | 0.951 *** | 820.630 *** | 18.734 *** | −21.264 *** | 0.829 | |
| L | 0.151 | −1.260 | 0.858 | −0.076 | −0.001 | 0.065 | 0.143 | 9.755 | 0.891 *** | 4324.821 *** | 16.220 * | −17.092 *** | 6.481 ** |
| Politician | Best-Fit Distribution |
|---|---|
| A | Noncentral t-distribution () |
| B | Johnson’s distribution ( = 0.21, ) |
| C | Noncentral t-distribution () |
| D | Lévy alpha-stable distribution (, ) |
| E | Johnson’s distribution (, ) |
| F | Lévy alpha-stable distribution (, ) |
| G | Noncentral t-distribution () |
| H | Noncentral t-distribution () |
| I | Noncentral t-distribution () |
| J | Noncentral t-distribution () |
| K | Noncentral t-distribution () |
| L | t-distribution () |
| 177 (93.65%) | 12 (6.35%) | |
| 183 (96.83%) | 6 (3.17%) | |
| 184 (97.35%) | 5 (2.65%) |
| Politically-Themed Stock | Politician-Related Search Volume | Rank | ETE Values | Rank |
|---|---|---|---|---|
| H-1 | 93,800 | 1 | 0.1266 | 1 |
| H-2 | 29,600 | 2 | 0.1024 | 6 |
| H-3 | 11,000 | 3 | 0.0506 | 9 |
| H-4 | 8660 | 4 | 0.1112 | 5 |
| H-5 | 8420 | 5 | 0.1251 | 2 |
| H-6 | 6410 | 6 | 0.1115 | 4 |
| H-7 | 5350 | 7 | 0.1157 | 3 |
| H-8 | 3560 | 8 | 0.0799 | 8 |
| H-9 | 2740 | 9 | 0.0872 | 7 |
| H-10 | 2280 | 10 | 0.0331 | 10 |
| 1716 (79.81%) | 434 (20.19%) | |
| 1741 (80.98%) | 409 (19.02%) | |
| 1760 (81.86%) | 390 (18.14%) |
| Politically-Themed Stock Networks | Leading Stocks | Following Stocks | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A | A-5 | A-7 | A-16 | A-2 | A-5 | A-7 | A-16 | ||
| B | B-3 | B-4 | B-5 | B-6 | B-4 | B-5 | B-7 | ||
| C | C-4 | C-7 | C-9 | C-20 | C-4 | C-9 | C-12 | C-20 | |
| D | D-1 | D-14 | D-1 | D-9 | D-14 | ||||
| E | E-1 | E-2 | E-4 | E-10 | E-1 | E-8 | E-9 | ||
| F | F-4 | F-13 | F-13 | F-14 | |||||
| G | G-1 | G-4 | G-8 | G-1 | G-3 | G-4 | G-6 | G-8 | |
| H | H-2 | H-4 | H-2 | H-4 | H-7 | H-8 | |||
| I | I-2 | I-8 | I-9 | I-1 | I-2 | I-8 | I-9 | ||
| J | J-1 | J-2 | J-13 | J-20 | J-1 | J-4 | J-20 | ||
| K | K-8 | K-9 | K-20 | K-9 | K-11 | K-20 | |||
| L | L-1 | L-6 | L-12 | L-6 | L-8 | L-11 | L-12 | ||
| Date | Name | Description |
|---|---|---|
| 13 April 2016 | Period 1 | Twentieth Legislative Election |
| 10 March 2017 | Period 2 | Impeachment of the Eighteenth President |
| 9 May 2017 | Period 3 | Nineteenth Presidential Election |
| 13 June 2018 | Period 4 | Seventh Local Election |
| 17 April 2019 | Period 5 | Control Point in Time |
| 15 April 2020 | Period 6 | Twenty-First Legislative Election |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, I.; Kim, W.C. Detecting and Analyzing Politically-Themed Stocks Using Text Mining Techniques and Transfer Entropy—Focus on the Republic of Korea’s Case. Entropy 2021, 23, 734. https://doi.org/10.3390/e23060734
Choi I, Kim WC. Detecting and Analyzing Politically-Themed Stocks Using Text Mining Techniques and Transfer Entropy—Focus on the Republic of Korea’s Case. Entropy. 2021; 23(6):734. https://doi.org/10.3390/e23060734
Chicago/Turabian StyleChoi, Insu, and Woo Chang Kim. 2021. "Detecting and Analyzing Politically-Themed Stocks Using Text Mining Techniques and Transfer Entropy—Focus on the Republic of Korea’s Case" Entropy 23, no. 6: 734. https://doi.org/10.3390/e23060734
APA StyleChoi, I., & Kim, W. C. (2021). Detecting and Analyzing Politically-Themed Stocks Using Text Mining Techniques and Transfer Entropy—Focus on the Republic of Korea’s Case. Entropy, 23(6), 734. https://doi.org/10.3390/e23060734







