A Simple Parallel Chaotic Circuit Based on Memristor
Abstract
1. Introduction
2. A Memristor–Thermistor Chaotic Circuit
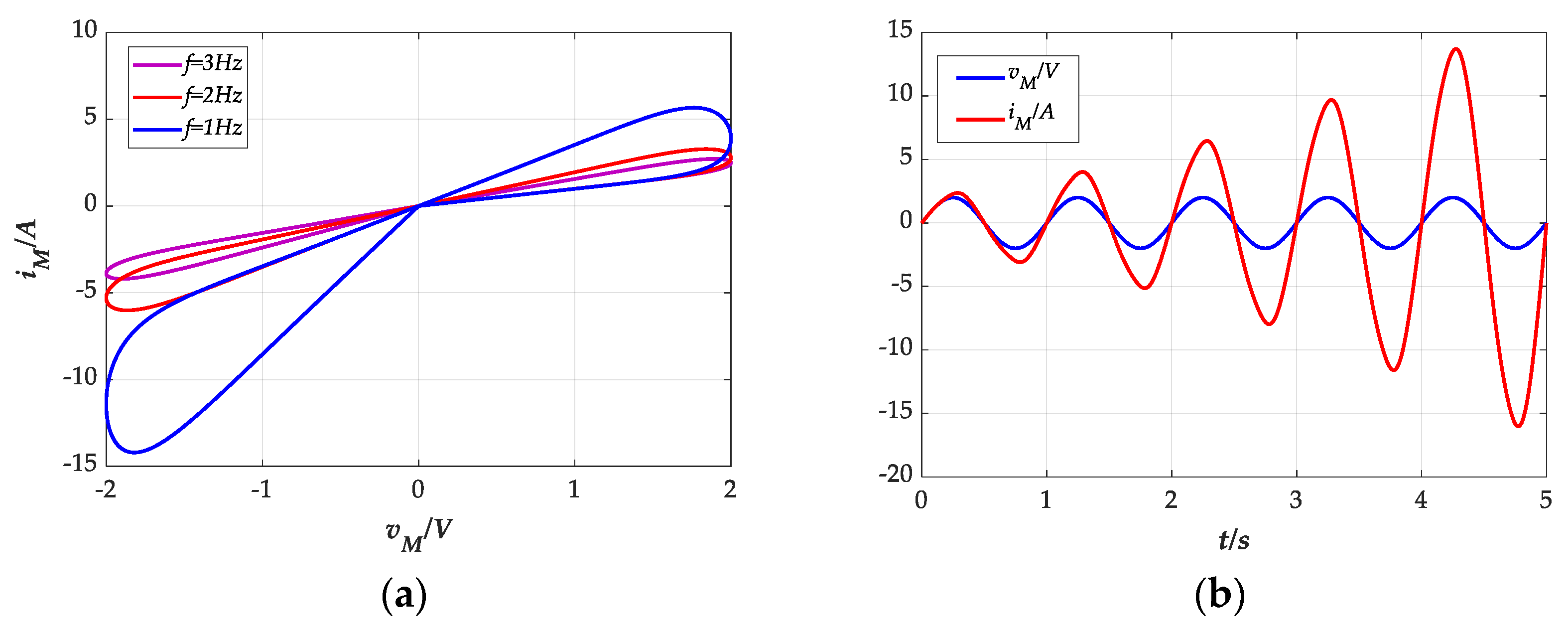
2.1. Model of Thermistor
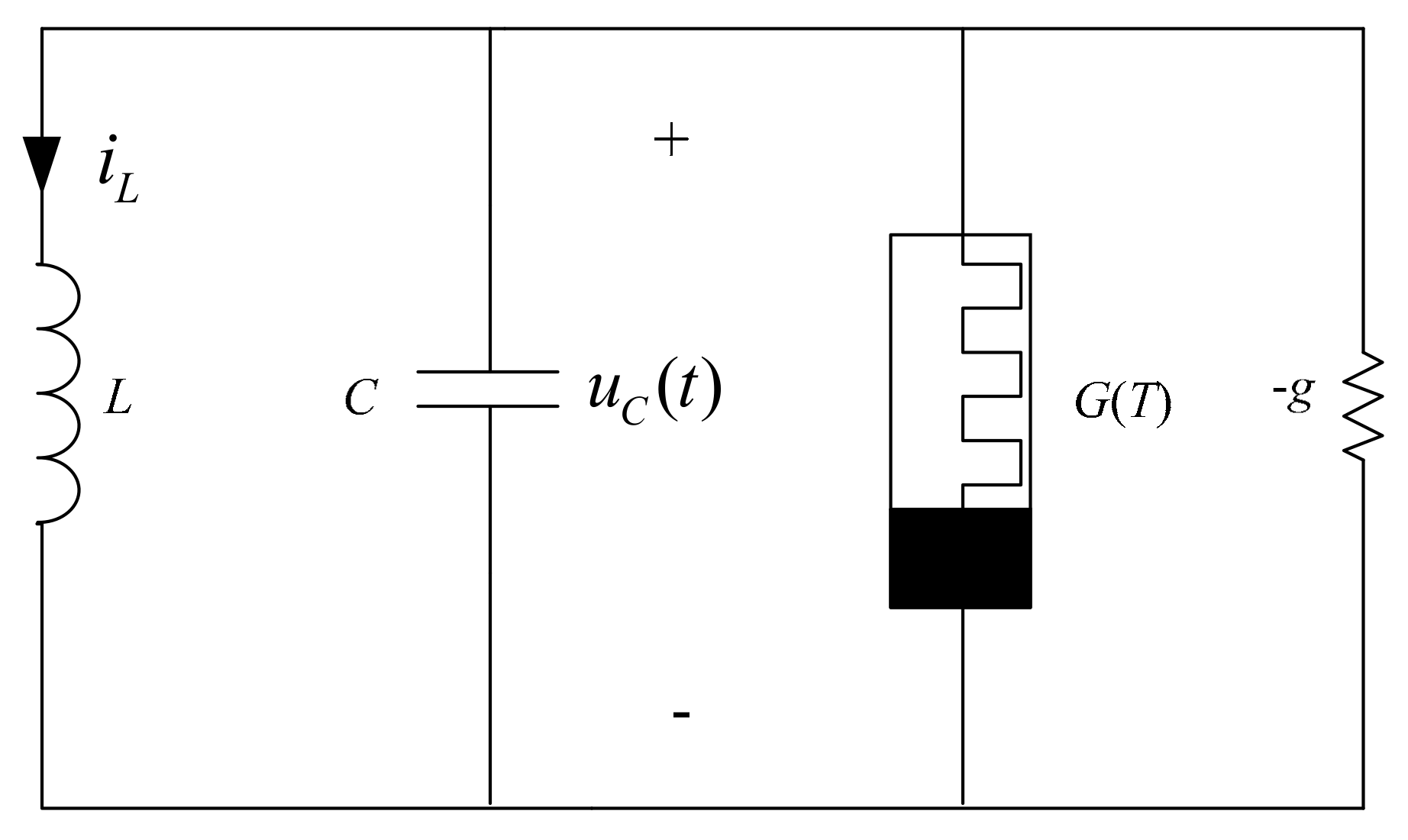
2.2. A Simple Chaotic Oscillator
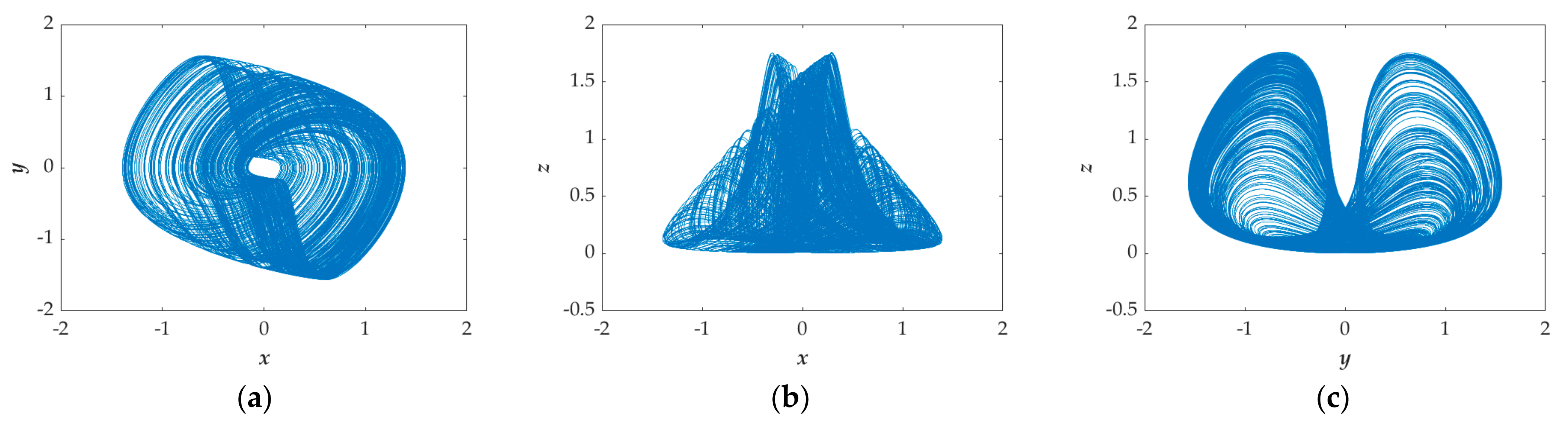
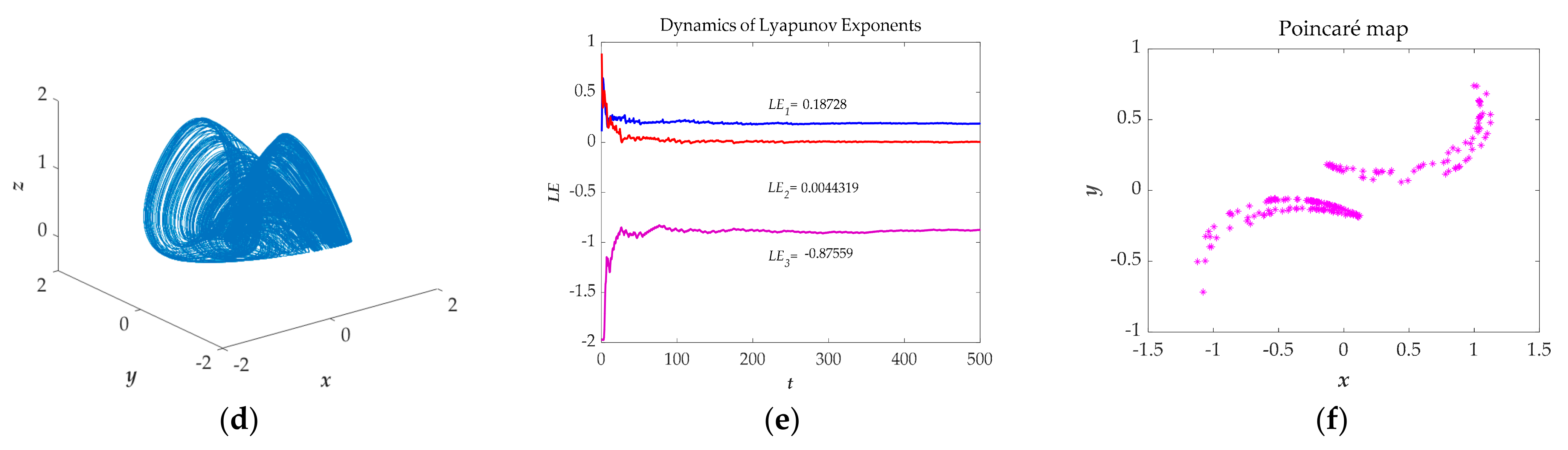
3. Dynamical Properties of the System
3.1. Equilibrium Analysis
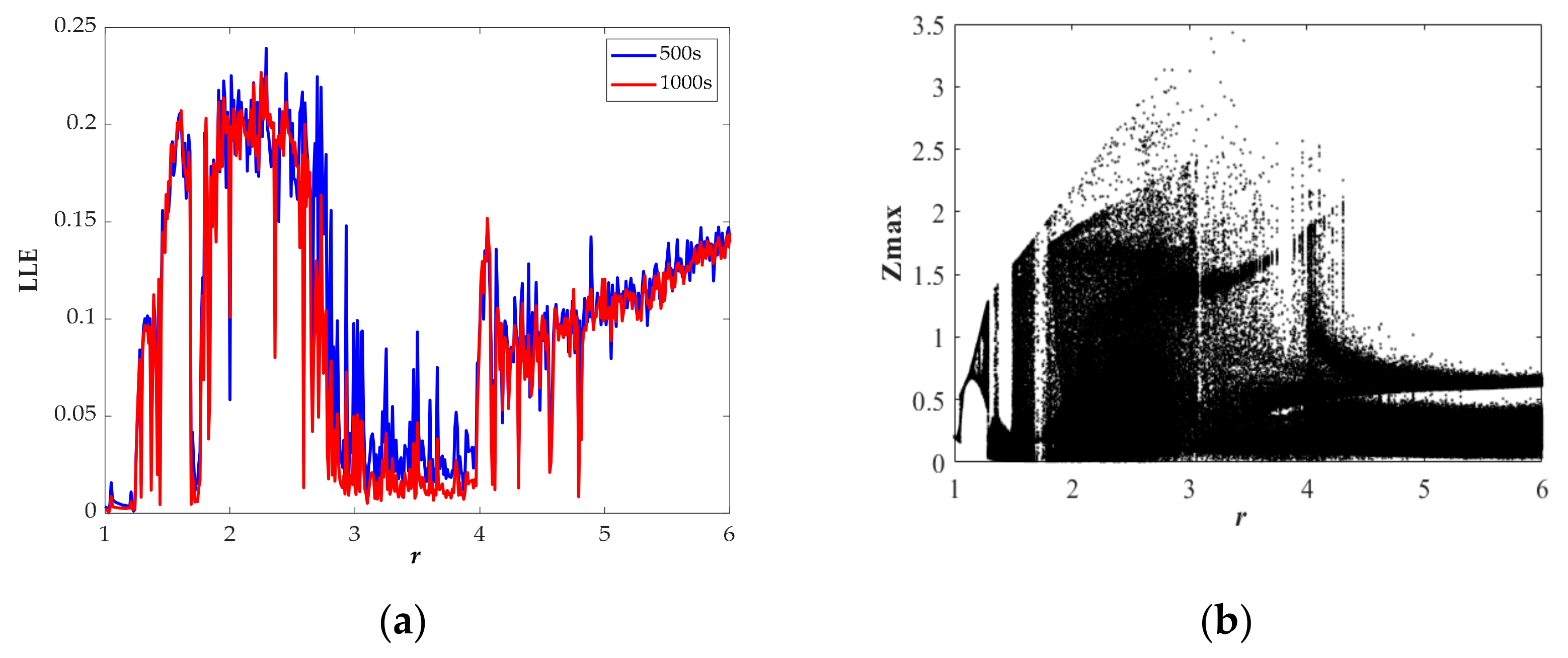
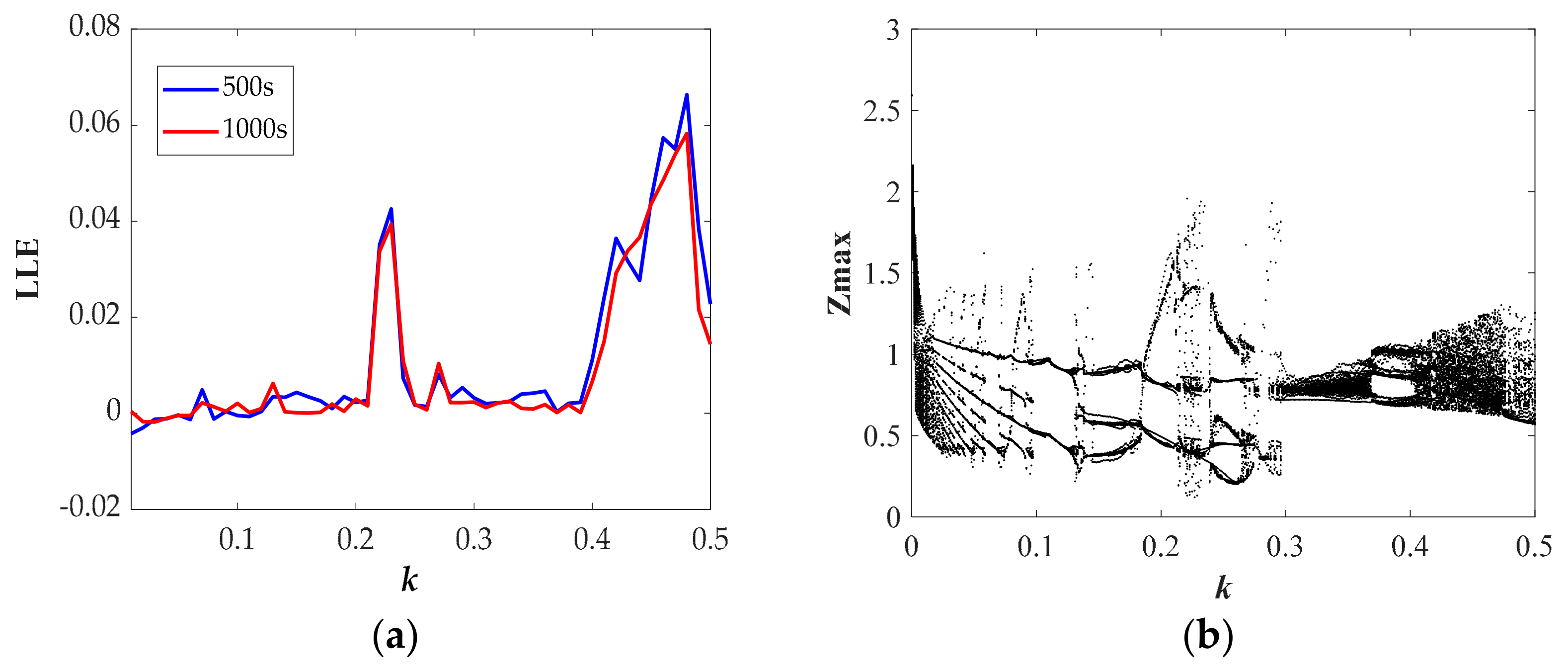
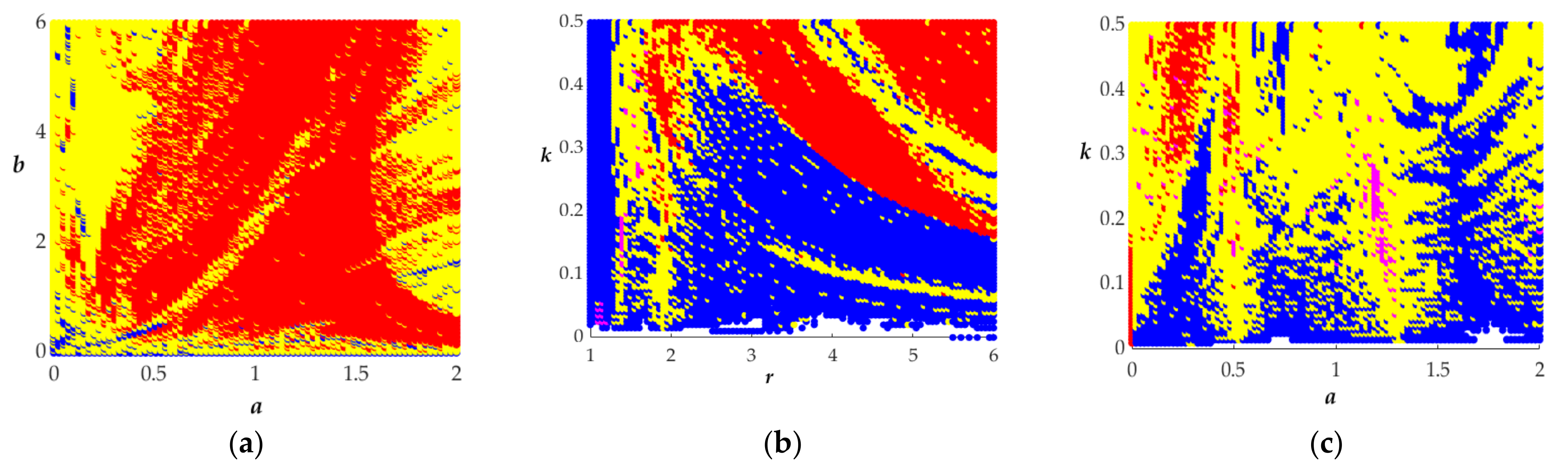
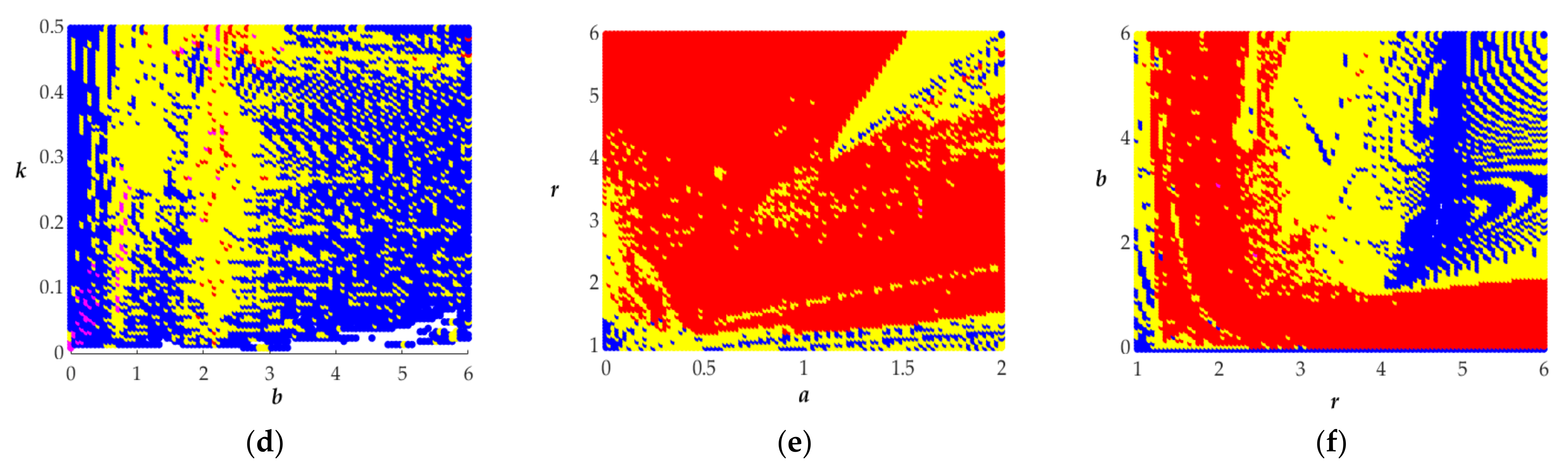
3.2. The Impacts of Parameters
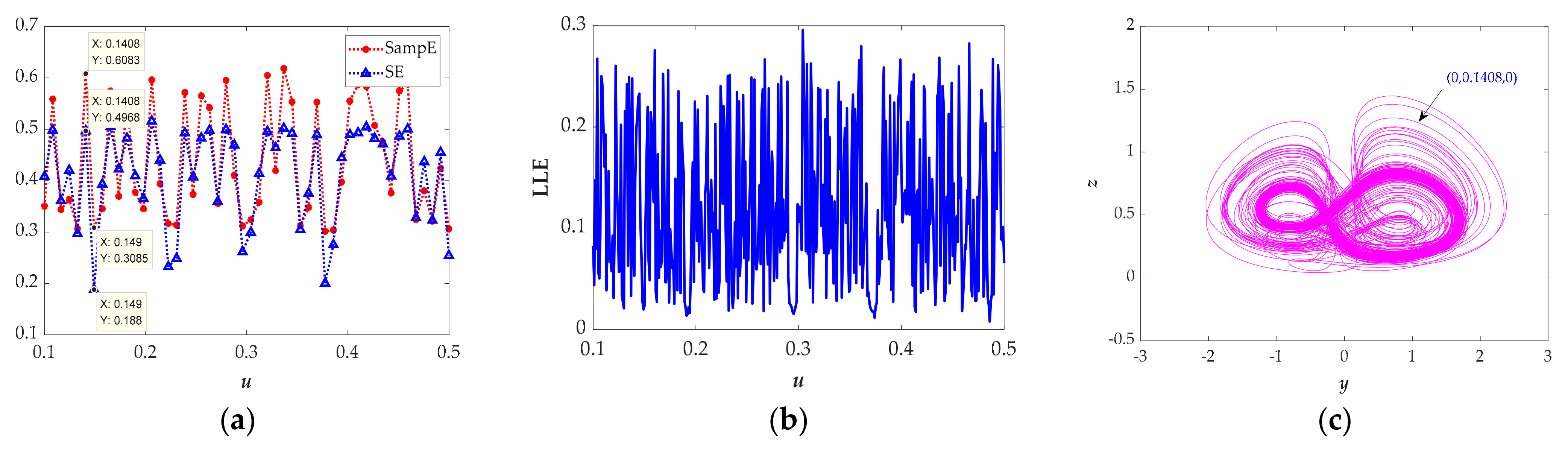
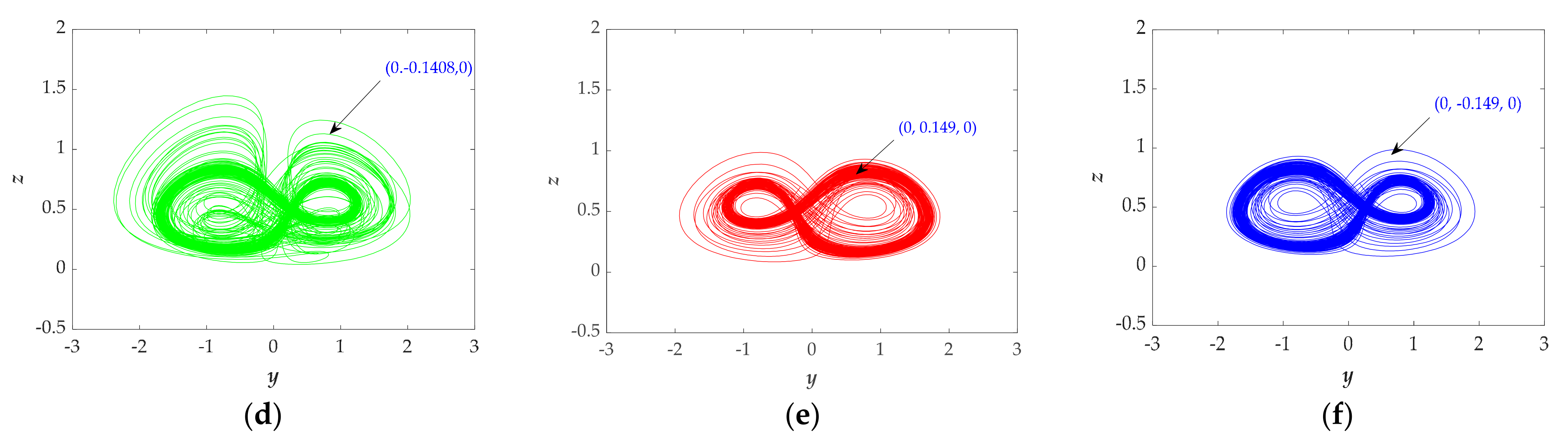
3.3. Coexistence of Attractors
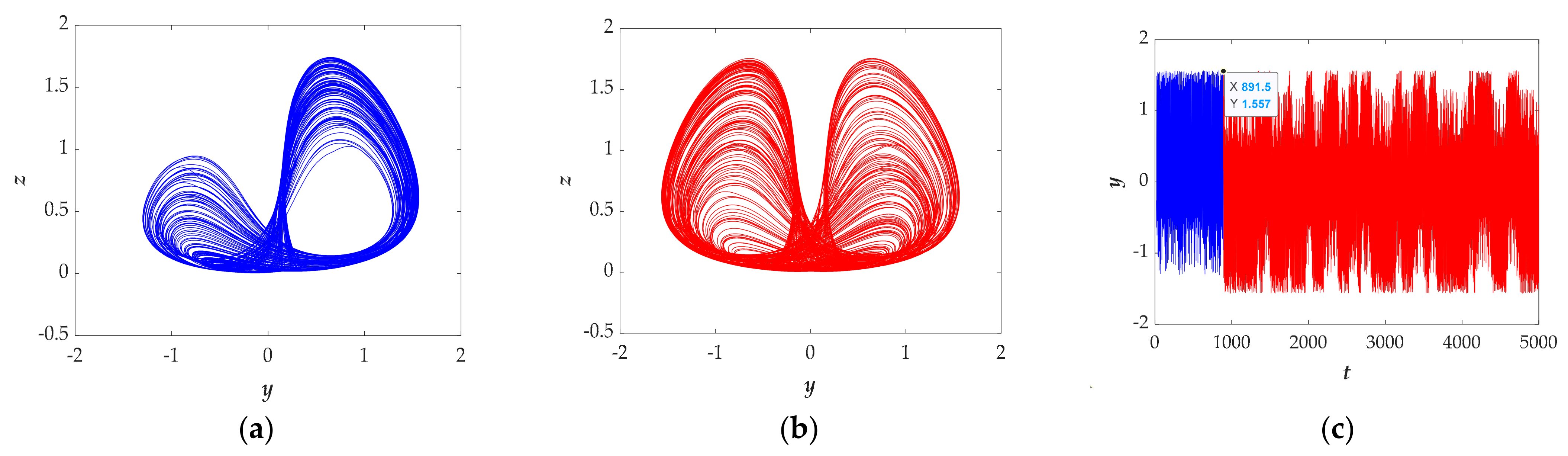
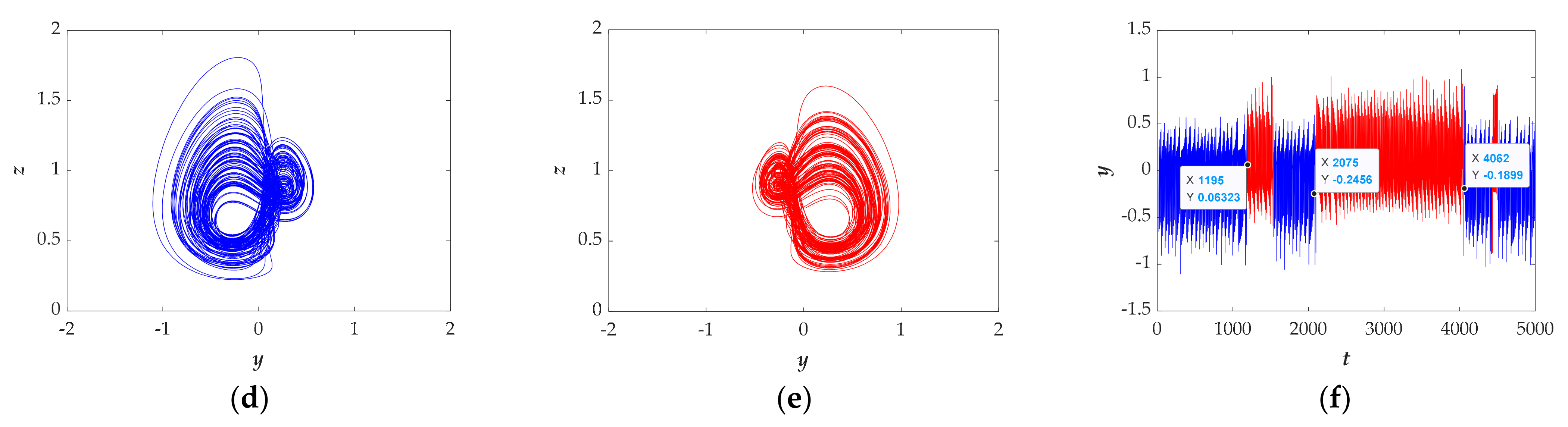
3.4. Transient Transition Behaviors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Pershin, Y.V.; Ventra, M.D. On the validity of memristor modeling in the neural network literature. Neural Netw. 2019, 121, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wu, H.; Gao, B.; Wu, W.; Xi, Y.; Yao, P. Associative memory for image recovery with a high-performance memristor array. Adv. Funct. Mater. 2019, 29, 1900155. [Google Scholar] [CrossRef]
- Chung, K.W.; Chan, C.L.; Xu, Z.; Mahmoud, G.M. A perturbation-incremental method for strongly nonlinear autonomous oscillators with many degrees of freedom. Nonlinear Dyn. 2002, 28, 243–259. [Google Scholar] [CrossRef]
- Mahmoud, G.M. Periodic solutions of strongly non-linear Mathieu oscillators. Int. J. Non-Linear Mech. 1997, 32, 1177–1185. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Chua, L.O. Simplest Chaotic Circuit. Int. J. Bifurc. Chaos 2010, 20, 1567–1580. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memristor Oscillators. Int. J. Bifurc. Chaos 2008, 18, 3183–3206. [Google Scholar] [CrossRef]
- Wang, G.; Zang, S.; Wang, X.; Yuan, F. Memcapacitor model and its application in chaotic oscillator with memristor. Chaos 2017, 27, 013110. [Google Scholar] [CrossRef]
- Sambas, A.; Mamat, M.; Arafa, A.A.; Mahmoud, G.M.; Sanjaya, W. A new chaotic system with line of equilibria: Dynamics, passive control and circuit design. Int. J. Electr. Comput. Eng. 2019, 9, 2365–2376. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M.E.; Sabor, N. On autonomous and non-autonomous modified hyperchaotic complex Lü systems. Int. J. Bifurc. Chaos 2011, 7, 1913–1926. [Google Scholar] [CrossRef]
- Du, C.; Liu, L.; Shi, S. Multiple Transient Transitions Behavior Analysis of a Double Memristor’s Hidden System and Its Circuit. IEEE Access 2020, 8, 76642–76656. [Google Scholar] [CrossRef]
- Takran, Z.; Saba, M.; Ayten, U.E.; Sedef, H. A new universal mutator circuit for memcapacitor and meminductor elements. AEU Int. J. Electron. Commun. 2020, 119, 1533–3180. [Google Scholar] [CrossRef]
- Alombah, N.H.; Fotsin, H.; Ngouonkadi, E.B.M.; Nguazon, T. Dynamics analysis and implementation of a multiscroll memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2016, 26, 1650128. [Google Scholar] [CrossRef]
- Deng, H.; Wang, D. A Memristor-based Colpitts like Oscillator. DEStech Trans. Eng. Technol. Res. 2016. [Google Scholar] [CrossRef][Green Version]
- Wu, J.; Wang, L.; Chen, G.; Duan, S. A memristive chaotic system with heart-shaped attractors and its implementation. Chaos Solitons Fractals 2016, 92, 20–29. [Google Scholar] [CrossRef]
- Yu, Q.; Bao, B.C.; Hu, F.W.; Quan, X.; Mo, C.; Jiang, W. Wien-bridge chaotic oscillator based on first-order generalized memristor. Acta Phys. Sin. 2014, 63, 240505–240511. [Google Scholar]
- Liu, L.; Du, C.; Liang, L.; Zhang, X. A high spectral entropy (SE) memristive hidden chaotic system with multi-type quasi-periodic and its circuit. Entropy 2019, 21, 1026. [Google Scholar] [CrossRef]
- Ye, X.; Mou, J.; Luo, C.; Wang, Z. Dynamics analysis of Wien-bridge hyper-chaotic memristive circuit system. Nonlinear Dyn. 2018, 92, 923–933. [Google Scholar] [CrossRef]
- Xu, B. A Simplest Parallel chaotic system of memristor. Acta Phys. Sin. 2013, 62, 99–106. [Google Scholar]
- Yuan, F.; Li, Y. A chaotic circuit constructed by a memristor, a memcapacitor and a meminductor. Chaos 2019, 29, 101101. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Mou, J.; Liu, J.; Ma, C.; Zhao, X. A novel simple chaotic circuit based on memristor—memcapacitor. Nonlinear Dyn. 2020, 100, 2859–2876. [Google Scholar] [CrossRef]
- Wu, H.; Ye, Y. Extremely slow passages in low-pass filter-based memristive oscillator. Nonlinear Dyn. 2019, 97, 2339–2353. [Google Scholar] [CrossRef]
- Bao, B.; Wang, N.; Xu, Q.; Wu, H.; Hu, Y. A simple third-order memristive band pass filter chaotic circuit. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 977–981. [Google Scholar] [CrossRef]
- Bao, B.C.; Wu, P.; Bao, H.; Chen, M. Chaotic bursting in memristive diode bridge-coupled sallen-key lowpass filter. Electron. Lett. 2017, 53, 1104–1105. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Muthuswamy, B.; Meucci, R.; Euzzor, S. A physical memristor based muthuswamy–chua–ginoux system. Sci. Rep. 2020, 10, 19206. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Wolf, A. Lyapunov exponent estimation from a time series. Documentation added. Acta Biochim. Pol. 2013, 60, 345–349. [Google Scholar]
- Dnb, A.; Dop, B.; Avt, B.; Dik, C.; Egn, D. New technique to quantify chaotic dynamics based on differences between semi-implicit integration schemes. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105467. [Google Scholar] [CrossRef]
- Holms, P. Poincaré, celestial mechanics, dynamical-systems theory and “chaos”. Phys. Rep. 1990, 193, 137–163. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Dynamics and entropy analysis for a new 4-D hyperchaotic system with coexisting hidden attractors. Entropy 2019, 21, 287. [Google Scholar] [CrossRef]
- Lauriten, B. Semiclassical Poincare map for integrable systems. Chaos 1992, 2, 409. [Google Scholar] [CrossRef]
- Kuznetsov, A.P.; Kuznetsov, S.P.; Mosekilde, E.; Stankevich, N.V. Co-existing hidden attractors in a radio-physical oscillator system. J. Phys. A Math. Theor. 2015, 48, 125101. [Google Scholar] [CrossRef]
- Teixera, J.; Reynolds, C.A.; Judd, K. Time step sensitivity of nonlinear atmospheric models:numerical convergence, truncation error growth, and ensemble design. J. Atmos. Sci. 2007, 64, 175. [Google Scholar] [CrossRef]
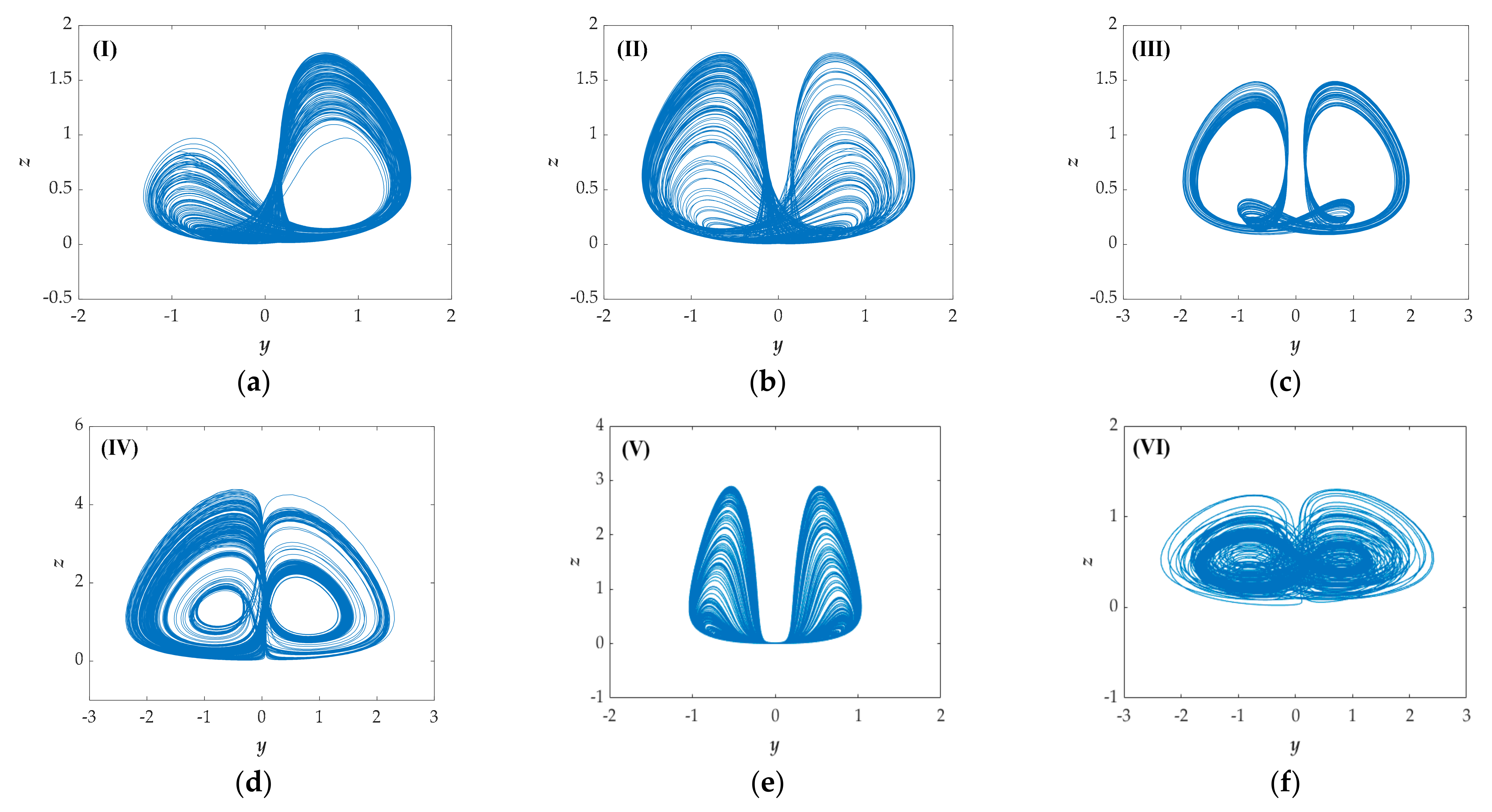
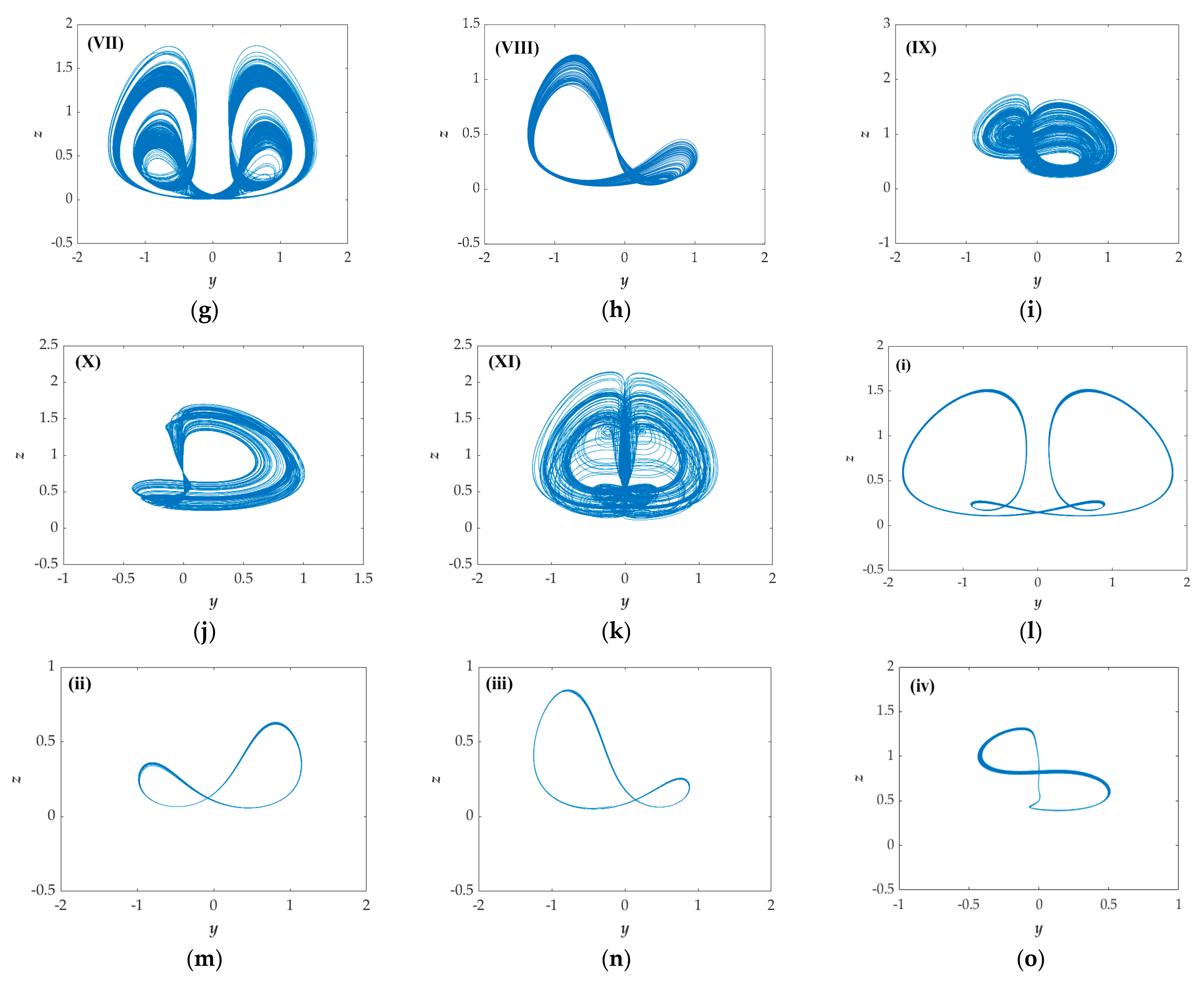
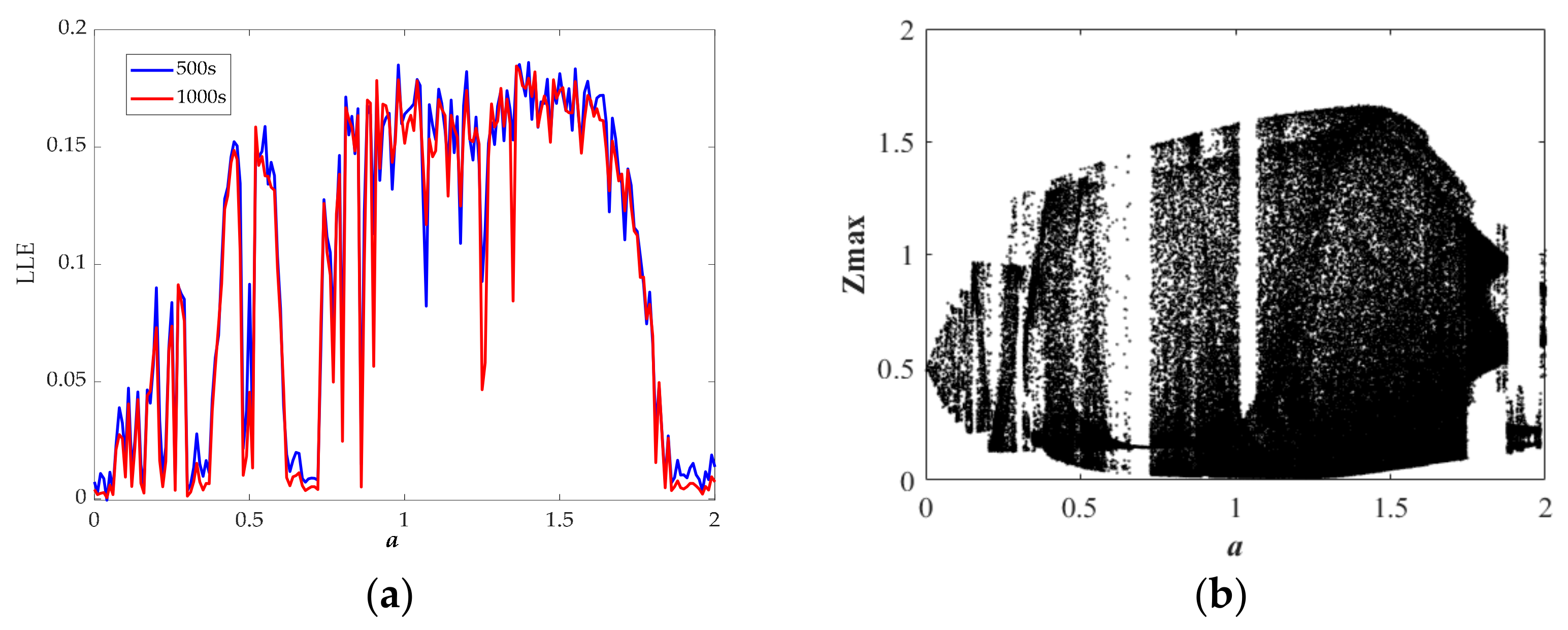
| Range (a) | LEs | State | Attractor Type |
|---|---|---|---|
| 0.17–0.20 | +0- | chaos | VII |
| 0.23–0.29 | +0- | chaos | VII |
| 0.52–0.58 | +0- | chaos | II |
| 0.64–0.72 | 0-- | period | i |
| 0.73–1.01 | +0- | chaos | II |
| 1.02–1.06 | +0- | chaos | VIII |
| 1.08–1.76 | +0- | chaos | II |
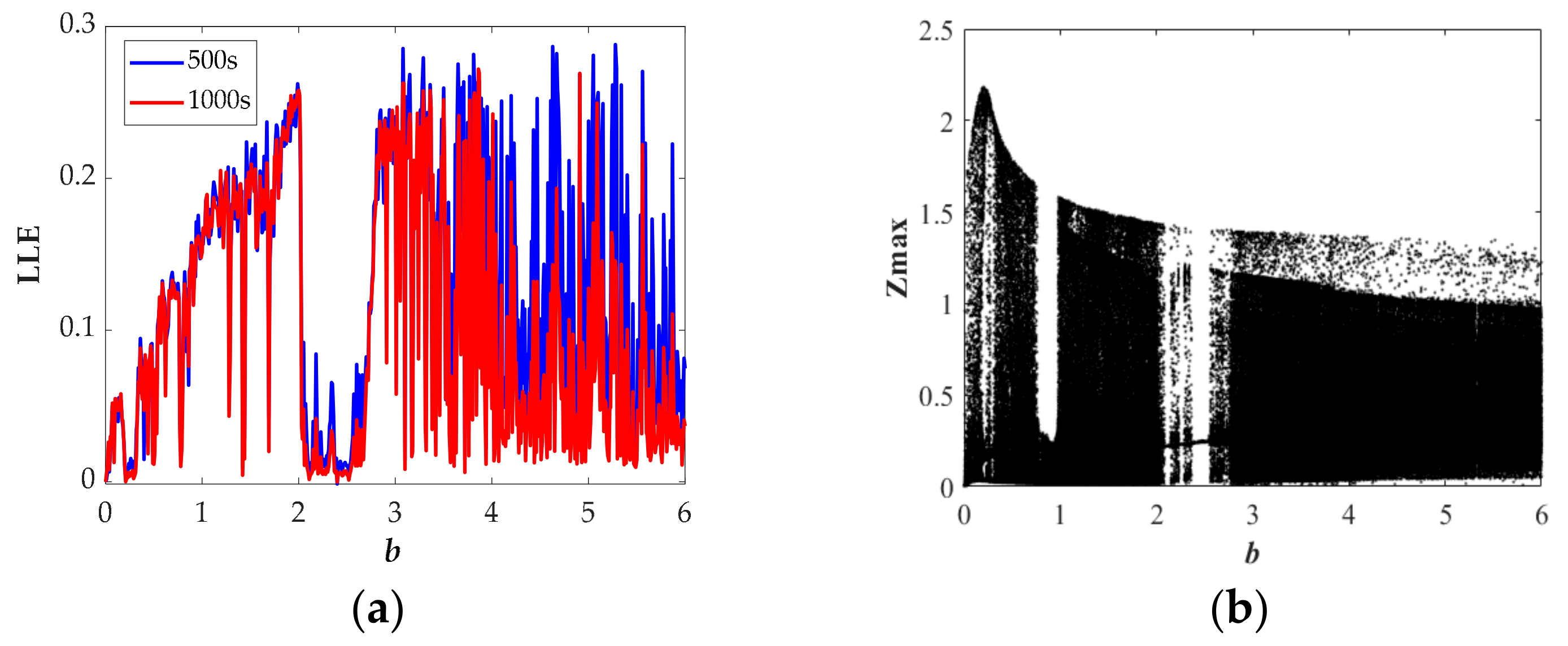
| Range (b) | LEs | State | Attractor Type |
|---|---|---|---|
| 0.06–0.19 | +0- | chaos | V |
| 0.33–0.55 | +0- | chaos | V |
| 0.56–0.74 | +0- | chaos | II |
| 0.80–0.97 | +0- | chaos | I |
| 0.98–2.01 | +0- | chaos | II |
| 2.09–2.14 | 0-- | period | i |
| 2.69–2.73 | +0- | chaos | III |
| 2.75–3.45 | +0- | chaos | II |
| 3.46–6.00 | +0- | chaos | VI |
| Range (r) | LEs | State | Attractor Type |
|---|---|---|---|
| 1.00–1.03 | 0-- | period | ii |
| 1.08–1.15 | 0-- | period | iii |
| 1.26–1.28 | +0- | chaos | VIII |
| 1.29–1.33 | +0- | chaos | I |
| 1.34–1.35 | +0- | chaos | II |
| 1.39–1.49 | +0- | chaos | I |
| 1.5–1.68 | +0- | chaos | II |
| 1.69–1.74 | 0-- | period | i |
| 1.85–2.64 | +0- | chaos | II |
| 4.20–6.00 | +0- | chaos | IV |
| Range (k) | LEs | State | Attractor Type |
|---|---|---|---|
| 0.06 | 0-- | period | iv |
| 0.10 | 0-- | period | iv |
| 0.13 | +0- | chaos | X |
| 0.22–0.23 | +0- | chaos | XI |
| 0.41–0.47 | +0- | chaos | IX |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Tian, Z.; Li, J.; Cui, Z. A Simple Parallel Chaotic Circuit Based on Memristor. Entropy 2021, 23, 719. https://doi.org/10.3390/e23060719
Zhang X, Tian Z, Li J, Cui Z. A Simple Parallel Chaotic Circuit Based on Memristor. Entropy. 2021; 23(6):719. https://doi.org/10.3390/e23060719
Chicago/Turabian StyleZhang, Xiefu, Zean Tian, Jian Li, and Zhongwei Cui. 2021. "A Simple Parallel Chaotic Circuit Based on Memristor" Entropy 23, no. 6: 719. https://doi.org/10.3390/e23060719
APA StyleZhang, X., Tian, Z., Li, J., & Cui, Z. (2021). A Simple Parallel Chaotic Circuit Based on Memristor. Entropy, 23(6), 719. https://doi.org/10.3390/e23060719







