Normalized Multivariate Time Series Causality Analysis and Causal Graph Reconstruction
Abstract
1. Introduction
2. An Overview of the Theory of Information Flow-Based Causality Analysis
2.1. Directed Graph, Uncertainty Propagation, and Causality
2.2. A Brief Stroll through the Theory and Recent Advances
If the evolution of an event, say, , is independent of another one, , then the information flow from to is zero.
3. Information Flow among Time Series and Algorithm for Multivariate Causal Inference
| Algorithm 1: Quantitative causal inference |
| Input : d time series Output: a DG , and IFs along edges initialize such that all vertexes are isolated; set a significance level ; for each do compute by (14); if is significant at level then add to ; record ; end end return , together with the IFs |
4. Normalization of the Causality among Multivariate Time Series
5. Application to Causal Graph Reconstruction
5.1. A Noisy Causal Network from Autoregressive Processes
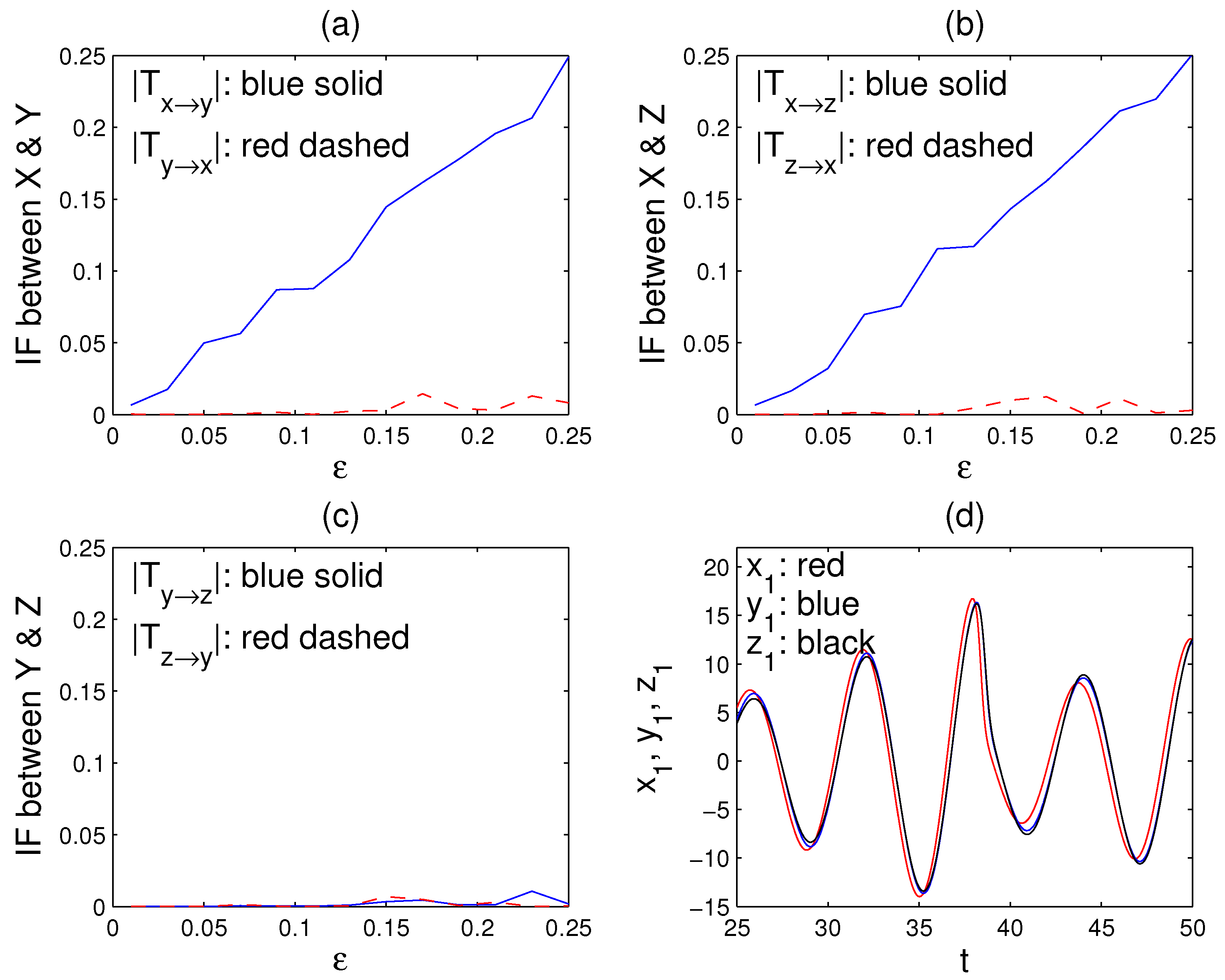
5.2. A Network of Nearly Synchronized Chaotic Series

6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schölkopf, B.; Janzing, D.; Peters, J.; Sgouritsa, E.; Zhang, K.; Mooij, J.M. On causal and anticausal learning. In Proceedings of the 29th International Conference on Machine Learning (ICML), Edinburgh, Scotland, UK, 26 June–1 July 2012; pp. 1255–1262. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Spirtes, P.; Glymour, C. An algorithm for fast recovery of sparse causal graphs. Soc. Sci. Comput. Rev. 1991, 9, 62–72. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef]
- Paluš, M.; Komárek, V.; Hrnčiř, Z.; Štěrbová, K. Synchronization as adjustment of information rates: Detection from bivariate time series. Phys. Rev. E 2001, 63, 046211. [Google Scholar] [CrossRef]
- Liang, X.S.; Kleeman, R. Information transfer between dynamical system components. Phys. Rev. Lett. 2005, 95, 244101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Spirtes, P. Detection of unfaithfulness and robust causal inference. Minds Mach. 2008, 18, 239–271. [Google Scholar] [CrossRef]
- Maathuis, M.H.; Colombo, D.; Kalisch, M.; Bühlmann, P. Estimating high-dimensional intervention effects from observation data. Ann. Stat. 2009, 37, 3133–3164. [Google Scholar] [CrossRef]
- Pompe, B.; Runge, J. Momentary information transfer as a coupling measure of time series. Phys. Rev. E 2011, 83, 051122. [Google Scholar] [CrossRef] [PubMed]
- Janzing, D.; Mooij, J.; Zhang, K.; Lemeire, J.; Zscheischler, J.; Daniušis, P.; Steudel, B.; Schölkopf, B. Information-geometric approach to inferring causal dierctions. Artif. Intell. 2012, 182, 1–31. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Sun, J.; Bollt, E. Causation entropy identifies indirect influences, dominance of neighbors, and anticipatory couplings. Physica D 2014, 267, 49–57. [Google Scholar] [CrossRef]
- Peters, J.; Janzing, D.; Schölkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Spirtes, P.; Zhang, K. Causal discovery and inference: Concepts and recent methodological advances. Appl. Inform. 2016, 3, 3. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow within stochastic dynamical systems. Phys. Rev. E 2008, 78, 031113. [Google Scholar] [CrossRef]
- Liang, X.S. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef] [PubMed]
- Røysland, K. Counterfactual analyses with graphical models based on local independence. Ann. Stat. 2012, 40, 2162–2194. [Google Scholar]
- Mooij, J.M.; Janzing, D.; Heskes, T.; Schölkopf, B. From ordinary differential equations to structural causal models: The deterministic case. In Proceedings of the 29th Annual Conference on Uncertainty in Artificial Intelligence, Bellevue, WA, USA, 11–15 July 2013; pp. 440–448. [Google Scholar]
- Mogensen, S.W.; Malinksky, D.; Hansen, N.R. Causal learning for partially observed stochastic dynamical systems. In Proceedings of the 34th Conference on Uncertainty in Artificial Intelligence (UAI), Monterey, CA, USA, 6–10 August 2018. [Google Scholar]
- Amigó, J.M.; Dale, R.; Tempesta, P. A generalized permutation entropy for noisy dynamics and random processes. Chaos 2021, 31, 013115. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Information flow with respect to relative entropy. Chaos 2018, 28, 075311. [Google Scholar] [CrossRef] [PubMed]
- Berkeley, G. A Treatise Concerning the Principles of Human Knowledge; Aaron Rhames: Dublin, Ireland, 1710. [Google Scholar]
- Liang, X.S.; Yang, X.-Q. A note on causation versus correlation in an extreme situation. Entropy 2021, 23, 316. [Google Scholar] [CrossRef] [PubMed]
- Hahs, D.W.; Pethel, S.D. Distinguishing anticipation from causality: Anticipatory bias in the estimation of information flow. Phys. Rev. Lett. 2011, 107, 12870. [Google Scholar] [CrossRef]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef] [PubMed]
- Hagan, D.F.T.; Wang, G.; Liang, X.S.; Dolman, H.A.J. A time-varying causality formalism based on the Liang-Kleeman information flow for analyzing directed interactions in nonstationary climate systems. J. Clim. 2019, 32, 7521–7537. [Google Scholar] [CrossRef]
- Vannitsem, S.; Dalaiden, Q.; Goosse, H. Testing for dynamical dependence—Application to the surface mass balance over Antarctica. Geophys. Res. Lett. 2019. [Google Scholar] [CrossRef]
- Hristopulos, D.T.; Babul, A.; Babul, S.; Brucar, L.R.; Virji-Babul, N. Dirupted information flow in resting-state in adolescents with sports related concussion. Front. Hum. Neurosci. 2019, 13, 419. [Google Scholar] [CrossRef] [PubMed]
- Garthwaite, P.H.; Jolliffe, I.T.; Jones, B. Statistical Inference; Prentice-Hall: Hertfordshire, UK, 1995. [Google Scholar]
- Liang, X.S. Normalizing the causality between time series. Phys. Rev. E 2015, 92, 022126. [Google Scholar] [CrossRef]
- Paluš, M.; Krakovská, A.; Jakubfk, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos 2018, 28, 075307. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.S. Normalized Multivariate Time Series Causality Analysis and Causal Graph Reconstruction. Entropy 2021, 23, 679. https://doi.org/10.3390/e23060679
Liang XS. Normalized Multivariate Time Series Causality Analysis and Causal Graph Reconstruction. Entropy. 2021; 23(6):679. https://doi.org/10.3390/e23060679
Chicago/Turabian StyleLiang, X. San. 2021. "Normalized Multivariate Time Series Causality Analysis and Causal Graph Reconstruction" Entropy 23, no. 6: 679. https://doi.org/10.3390/e23060679
APA StyleLiang, X. S. (2021). Normalized Multivariate Time Series Causality Analysis and Causal Graph Reconstruction. Entropy, 23(6), 679. https://doi.org/10.3390/e23060679





