Optimum Placement of Distribution Generation Units in Power System with Fault Current Limiters Using Improved Coyote Optimization Algorithm
Abstract
1. Introduction
Related Work
2. Analytical Modeling
Types of DG Units for Distribution Networks
- Type 1:
- In this type, active and reactive powers are capable by DGs.
- Type 2:
- Active power is managed by DGs only with a unity power factor, such as micro-turbines.
- Type 3:
- Reactive power is controlled by DGs, such as a synchronous compensator.
- Type 4:
- Consumption of reactive power with an injection of active power is a capability of DGs. This type includes a fixed-speed squirrel cage induction generator.
3. Methodology for Proper Allocation of DGs and FCLs
Novelties and Contribution of the Proposed ICOA
4. Results and Discussion
- Case 1:
- DGs working at a unity power factor and related to Type 3.
- Case 2:
- The power factor is kept constant for DGs, related to Type 1.
- Case 3:
- Controllable power factor technique is used for DGs.
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Shaheen, A.M.; El-Sehiemy, R.A. Optimal coordinated allocation of distributed generation units/capacitor banks/voltage regulators by EGWA. IEEE Syst. J. 2021, 15, 257–264. [Google Scholar] [CrossRef]
- Talaat, H.E.A.; Al-Ammar, E. Optimal allocation and sizing of distributed generation in distribution networks using genetic algorithms. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar]
- Musa, I.; Gadoue, S.; Zahawi, B. Integration of distributed generation in power networks considering constraints on discrete size of distributed generation units. Electr. Power Compon. Syst. 2014, 42, 984–994. [Google Scholar] [CrossRef]
- Porkar, S.; Poure, P.; Abbaspour-Tehrani-fard, A.; Saadate, S. Optimal allocation of distributed generation using a two-stage multi-objectivemixed-integer-nonlinear programming. Eur. Trans. Electr. Power 2011, 21, 1072–1087. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Matar, W.; Elshurafa, A.M. Electricity transmission formulations in multi-sector national planning models: An illustration using the KAPSARC energy model. Energy Rep. 2018, 4, 328–340. [Google Scholar] [CrossRef]
- Mehta, P.; Bhatt, P.; Pandya, V. Optimal selection of distributed generating units and its placement for voltage stability enhancement and energy loss minimization. Ain Shams Eng. J. 2018, 9, 187–201. [Google Scholar] [CrossRef]
- Abou EL-Ela, A.A.; El-Sehiemy, R.; Abbas, A. Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using water cycle algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Abdelwaness, M.; Abaza, A.; El-Sehiemy, R.A.; Nabil, M.; Rezk, H. Parameter estimation of electric power transformers using coyote optimization algorithm with experimental verification. IEEE Access 2020, 8, 50036–50044. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Nouh, A.S. Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules. Energy 2019, 187, 116001. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Ellien, A.R. Optimal Allocation of Distributed Generation Units Correlated with Fault Current Limiter Sites in Distribution Systems. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Alam, M.S.; Abido, M.A.Y.; El-Amin, I. Fault Current Limiters in Power Systems: A Comprehensive Review. Energies 2018, 11, 1025. [Google Scholar] [CrossRef]
- Abdel-mawgouda, H.; Kamelab, S.; Yub, J.; Jurado, F. Hybrid Salp Swarm Algorithm for integrating renewable distributed energy resources in distribution systems considering annual load growth. J. King Saud Univ. Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Hamidi, M.E.; Chabanloo, R.M. Optimal allocation of distributed generation with optimal sizing of fault current limiter to reduce the impact on distribution networks using NSGA-II. IEEE Syst. J. 2019, 13, 1714–1724. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Truong, A.V.; Phung, T.A. A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network. Int. J. Electr. Power Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Izzatillaev, J.O. Determination of Power Flows in Microgrids with Renewable Energy Sources by Using Special Computer Programs. Appl. Sol. Energy 2020, 56, 149–155. [Google Scholar] [CrossRef]
- Iqbal, F.; Khan, M.T.; Siddiqui, A.S. Optimal placement of DG and DSTATCOM for loss reduction and voltage profile improvement. Alex. Eng. J. 2018, 57, 755–765. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Kinawy, A.; Mouwafi, M. Optimal capacitor placement in distribution systems for power loss reduction and voltage profile improvement. IET Gener. Transm. Distrib. 2016, 10, 1209–1221. [Google Scholar] [CrossRef]
- Elsayed, A.M.; Mishref, M.M.; Farrag, S.M. Distribution system performance enhancement (Egyptian distribution system real case study). Int. Trans. Electr. Energy Syst. 2018, 28, e2545. [Google Scholar] [CrossRef]
- Arulraj, R.; Kumarappan, N. Optimal economic-driven planning of multiple DG and capacitor in distribution network considering different compensation coefficients in feeder’s failure rate evaluation. Eng. Sci. Tech. Int. J. 2019, 22, 67–77. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open Source Python Tool for Convenient Modeling, Analysis and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- Youssef, E.; El Azab, R.M.; Amin, A.M. Influence study of concentrated photovoltaic location on voltage stability. Int. J. Smart Grid Clean Energy 2015, 4, 226–232. [Google Scholar] [CrossRef]
- Stavros, K.; Aristidou, P.; Ulbig, A.; Koch, S.; Hug, G. Optimal planning of distribution grids considering active power curtailment and reactive power control. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Sa’ed, J.A.; Amer, M.; Bodair, A.; Baransi, A.; Favuzza, S.; Zizzo, G. A Simplified Analytical Approach for Optimal Planning of Distributed Generation in Electrical Distribution Networks. Appl. Sci. 2019, 9, 5446. [Google Scholar] [CrossRef]
- Swain, K.P.; De, M. DSM for All Day Voltage Profile Improvement in a Microgrid. IET Renew. Power Gener. 2019, 13, 990–997. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Wen, F.; Tseng, C.-L.; Zhao, X.; Wang, Q. An Integrated Planning Strategy for a Power Network and the Charging Infrastructure of Electric Vehicles for Power System Resilience Enhancement. Energies 2019, 12, 3918. [Google Scholar] [CrossRef]
- Niitsoo, J.; Jarkovoi, M.; Taklaja, P.; Klüss, J.; Palu, I. Power Quality Issues Concerning Photovoltaic Generation in Distribution Grids. Smart Grid Renew. Energy 2015, 6, 148–163. [Google Scholar] [CrossRef]
- Sanchez-Hidalgo, M.-A.; Cano, M.-D. A survey on visual data representation for smart grids control and monitoring. Sustain. Energy Grids Netw. 2018, 16, 351–369. [Google Scholar] [CrossRef]
- Pierezan, J.; Maidl, G.; Yamao, E.M.; Coelho, L.D.S.; Mariani, C.V. Cultural coyote optimization algorithm applied to a heavy duty gas turbines operation. Energy Convers. Manag. 2019, 199, 111932. [Google Scholar] [CrossRef]
- Guvenç, U.; Kaymaz, E. Economic dispatch integrated wind power using coyote optimization algorithm. In Proceedings of the 7th International Istanbul Smart Grids and Cities Congress and Fair, Istanbul, Turkey, 25–26 April 2019; pp. 179–183. [Google Scholar]
- Nguyen, T.T.; Vo, D.N.; Van Tran, H.; Van Dai, L. Optimal dispatch of reactive power using modified stochastic fractal search algorithm. Complexity 2019, 2019, 4670820. [Google Scholar] [CrossRef]
- Betka, A.; Terki, N.; Toumi, A.; Dahmani, H. Grey Wolf optimizer-based learning automata for solving block matching problem. Signal Image Video Process. 2020, 14, 285–293. [Google Scholar] [CrossRef]
- Pierezan, J.; Coelho, L.D.S. Coyote optimization algorithm: A new metaheuristic for global optimization problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]

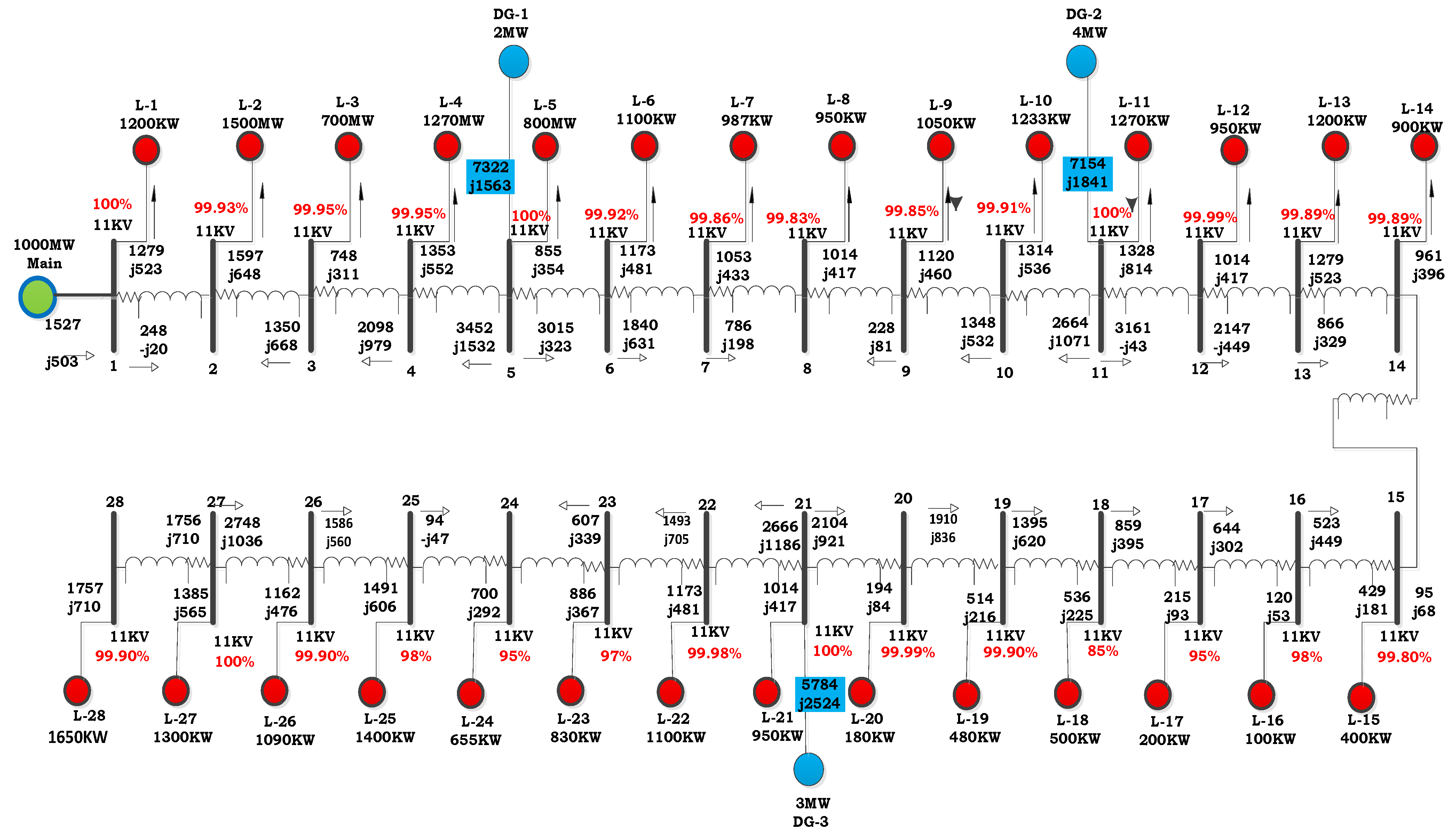
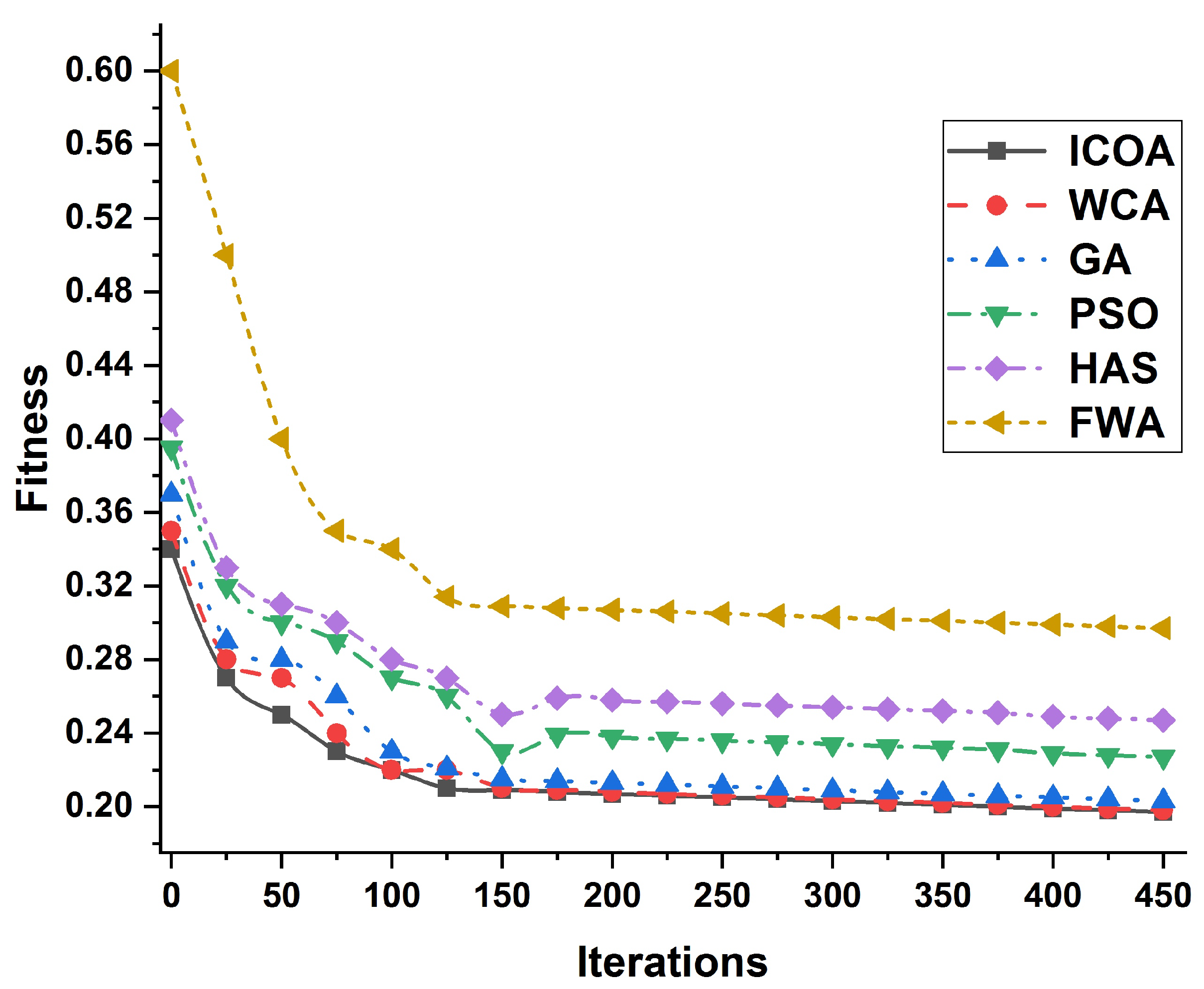
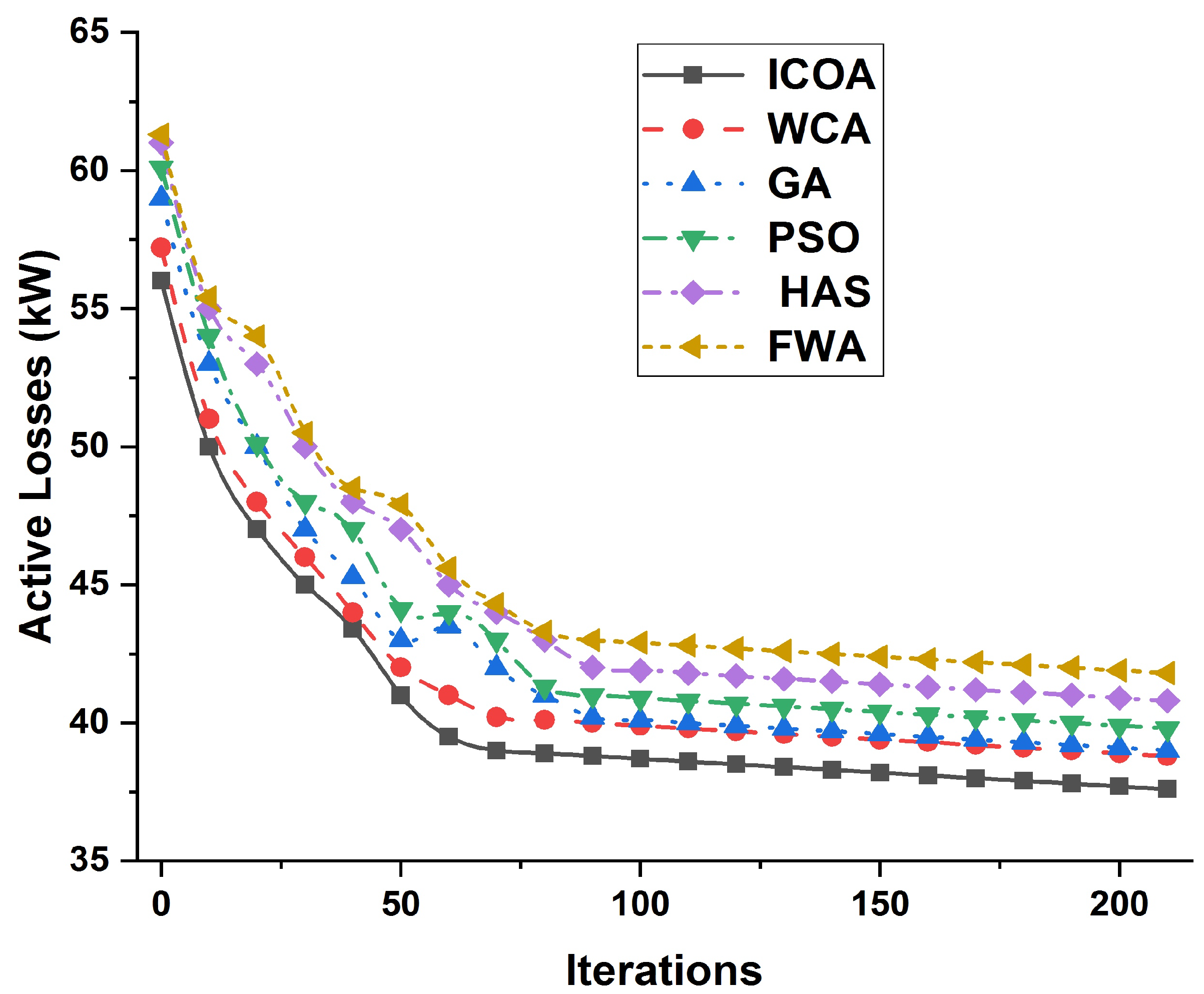
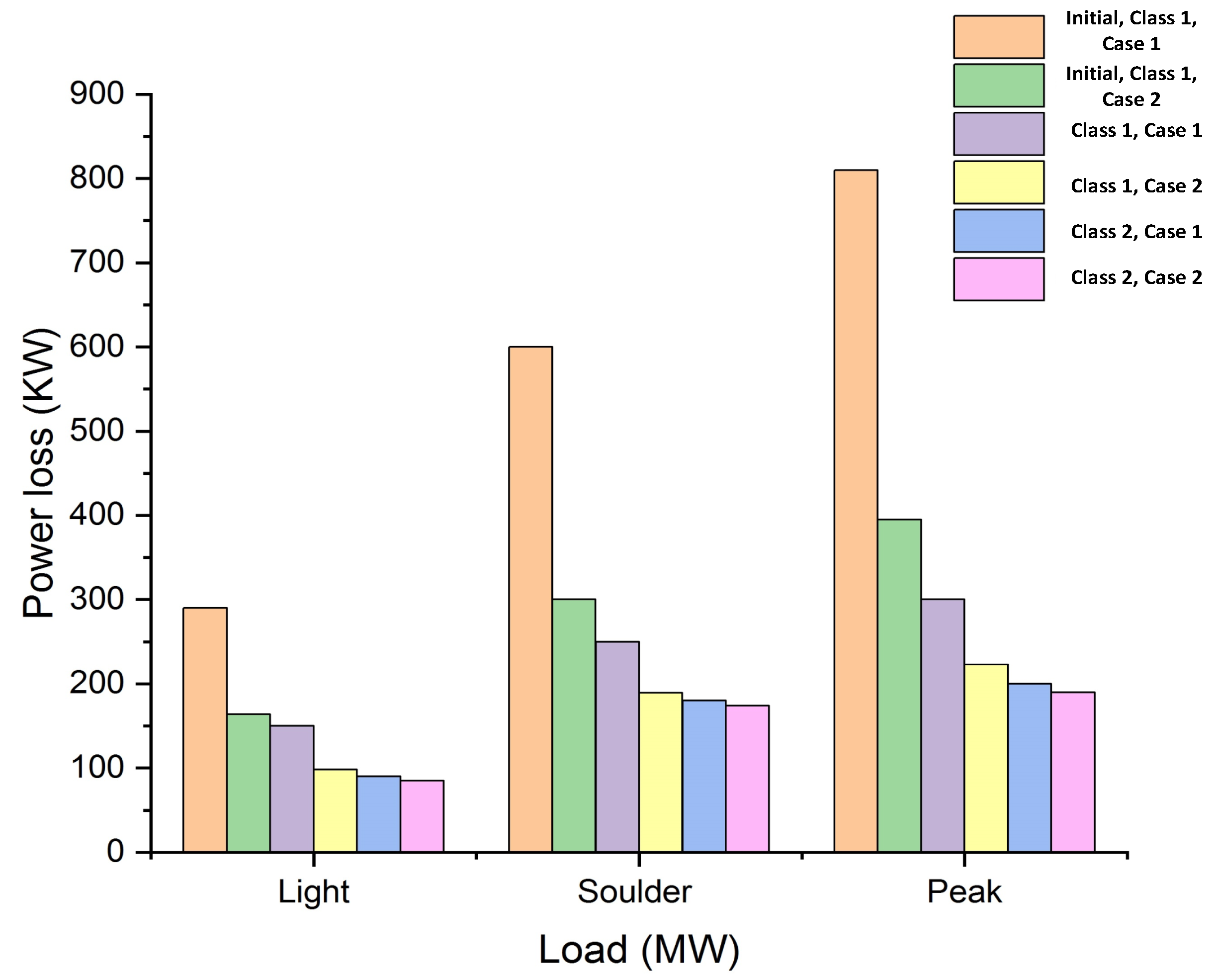
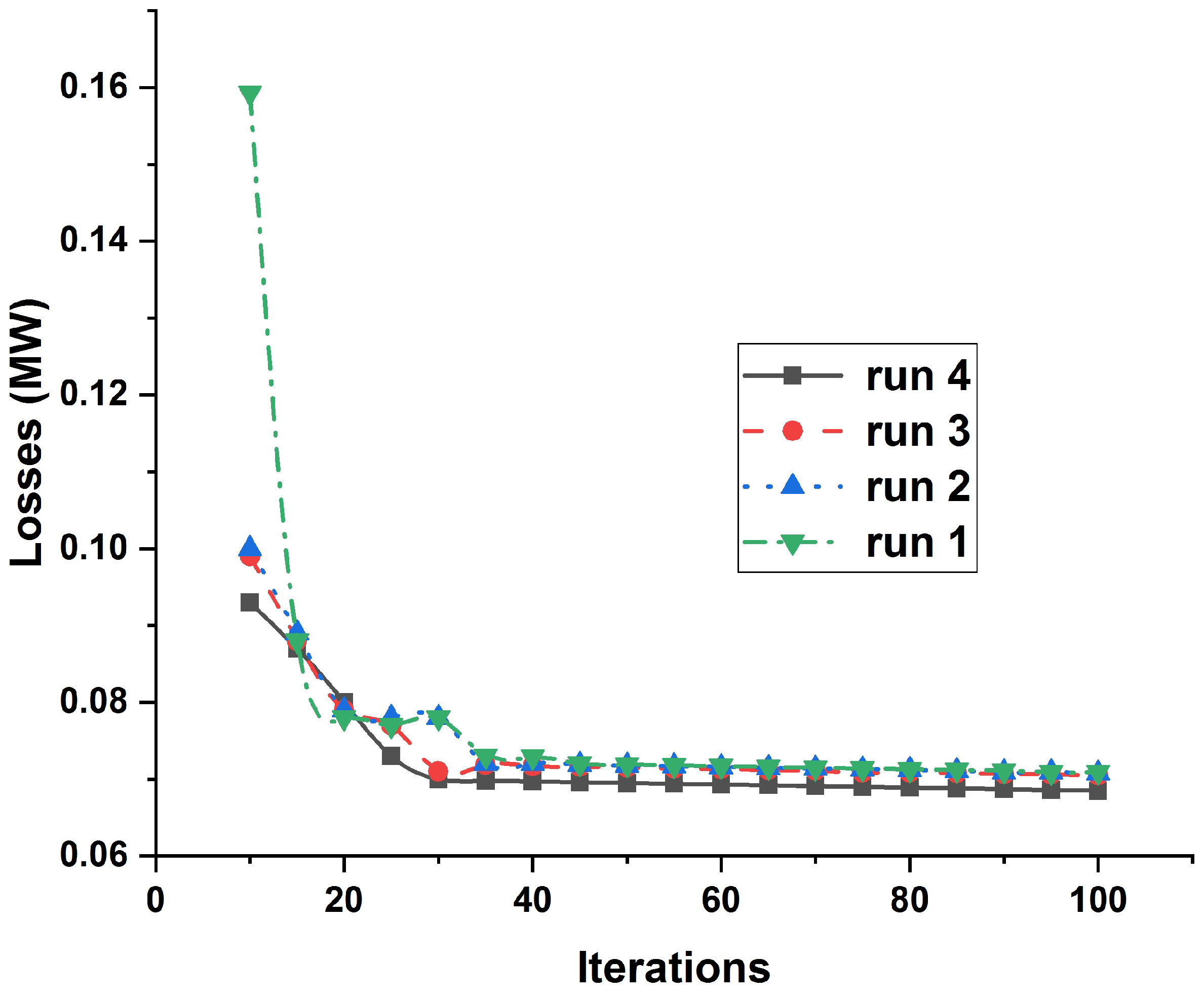
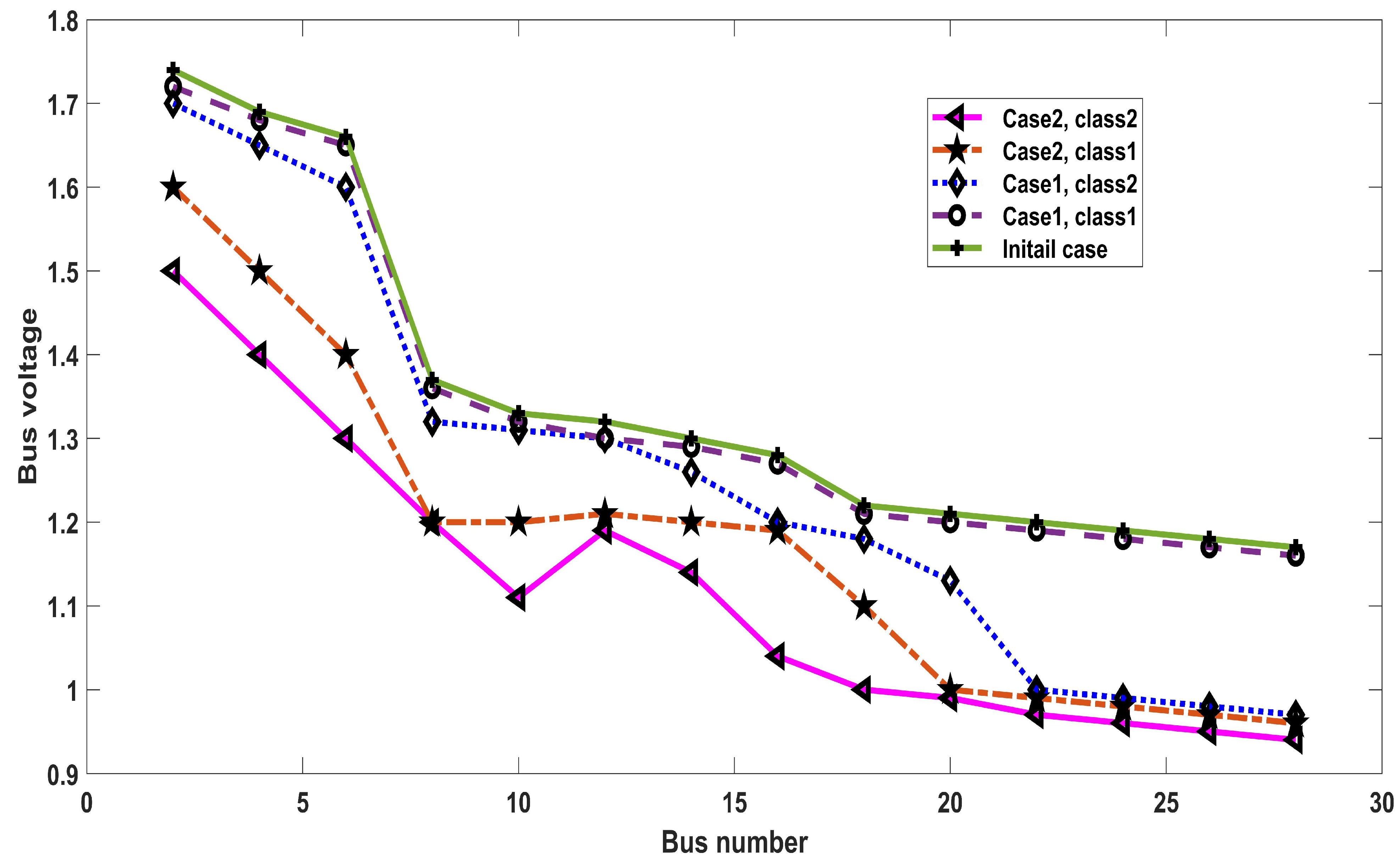
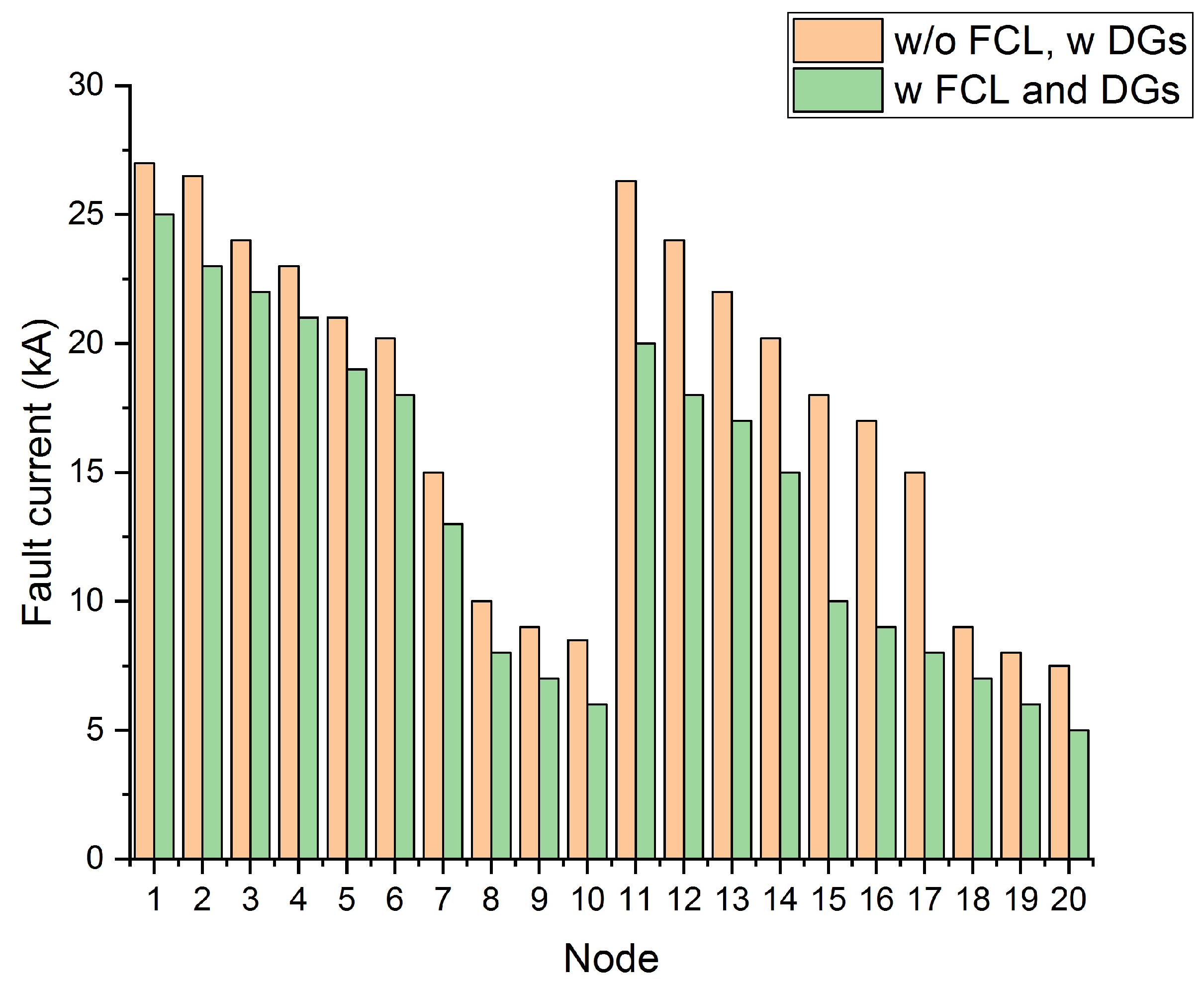
| Mechanism | KW (Losses) | DG Size/Placement | Min Voltage (P.U) Bus |
|---|---|---|---|
| TA [8] | 89.214 | 0.5897(14), 0.189(18), 1.0146(21) | 0.968 |
| FWA [16] | 98.3 | 0.633(17), 0.09(18), 0.947(27) | 0.964 |
| HAS [15] | 96.76 | 0.5724(17), 0.107(18), 1.0462(19) | 0.967(24) |
| BFOA [27] | 103.4 | 0.925(11), 0.863(16), 1.2(21) | 0.98(25) |
| PSO [28] | 105.35 | 1.1768(8), 0.9816(13), 0.8297(24) | 0.98(21) |
| GA [1] | 106.3 | 1.5(11), 0.4228(29), 1.0714(20) | 0.981(25) |
| WCA [14] | 72.9 | 0.8546(14), 1.1017(24), 1.181(29) | 0.97(16) |
| ICOA | 40.35 | 2(5), 4(11), 3(21) | 0.988(8) |
| KW (Losses) | DG Size/Placement | Min Voltage (P.U) Bus | Power Factor | |
|---|---|---|---|---|
| Initial | 213.78 | - | 0.99(17) | - |
| Case 2 | 17.54 | 0.8232(12), 1.1397(22), 1.12(26) | 0.994(7) | 0.84–0.85 |
| Case 3 | 12.8 | 0.837(12), 1.124(22), 1.07(26) | 0.994(7) | 0.75–0.86 |
| Framework | Losses (KW) | DG Size/Placement |
|---|---|---|
| ETAP-Bi Stage | 44.341 | 5.874(6), 8(16), 5.074(22) |
| COA (One Stage) | 44.815 | 7.783(16), 5.6056(22), 5.8189(9) |
| ICOA (One Stage) | 42.132 | 2(5), 4(11), 3(21) |
| Network | 28-Bus System | ||
|---|---|---|---|
| Method | PSO | COA | ICOA |
| Min(MW) | 0.817 | 0.0715 | 0.0690 |
| Mean(MW) | 0.0758 | 0.0739 | 0.0701 |
| Max(MW) | 0.0723 | 0.0794 | 0.0694 |
| Std | 0.0026 | 0.0020 | 0.0013 |
| Losses (KW) | DG Size (MW) and Location | DGu Power Factor | Min. Voltage Profile % (Bus) | ||
|---|---|---|---|---|---|
| Initial | 4871.6 | – | – | 80.34(28) | |
| COA | Different power factor | 14.43 | 0.71245(14), 1.0379(24), 1.2004(27) | 0.85, 0.85, 0.85 | 99.2(8) |
| Constant Power Factor | 11.7 | 0.7294(14), 1.0538(24), 1.0953(27) | 0.8951, 0.9024, 0.7302 | 99.2(8) | |
| ICOA | Different power factor | 15.12 | 2(5), 4(11), 3(21) | 0.8951, 0.9024, 0.7302 | 99.12(7) |
| Constant Power Factor | 10.34 | 2(5), 4(11), 3(21) | 0.85, 0.85, 0.85 | 99.12(7) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, H. Optimum Placement of Distribution Generation Units in Power System with Fault Current Limiters Using Improved Coyote Optimization Algorithm. Entropy 2021, 23, 655. https://doi.org/10.3390/e23060655
Alghamdi H. Optimum Placement of Distribution Generation Units in Power System with Fault Current Limiters Using Improved Coyote Optimization Algorithm. Entropy. 2021; 23(6):655. https://doi.org/10.3390/e23060655
Chicago/Turabian StyleAlghamdi, Hisham. 2021. "Optimum Placement of Distribution Generation Units in Power System with Fault Current Limiters Using Improved Coyote Optimization Algorithm" Entropy 23, no. 6: 655. https://doi.org/10.3390/e23060655
APA StyleAlghamdi, H. (2021). Optimum Placement of Distribution Generation Units in Power System with Fault Current Limiters Using Improved Coyote Optimization Algorithm. Entropy, 23(6), 655. https://doi.org/10.3390/e23060655






