AutoPPI: An Ensemble of Deep Autoencoders for Protein–Protein Interaction Prediction
Abstract
1. Introduction
2. Literature Review
3. Methodology
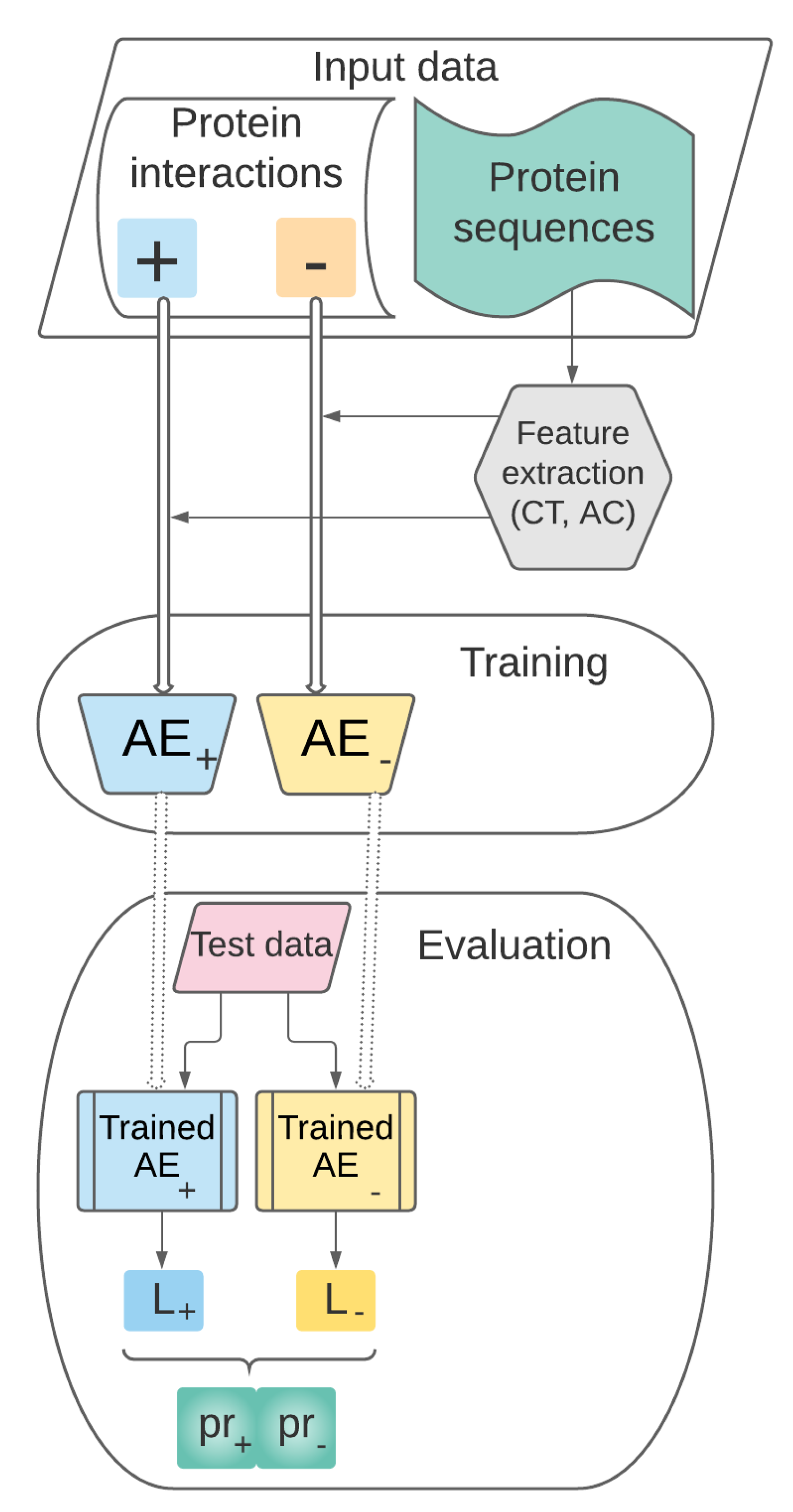
3.1. Theoretical Model
- Data collection, representation and preprocessing. This stage includes the following steps:
- i.
- Collection of data sets which will be used in further training (i.e., the pairs of proteins from );
- ii.
- Selection of the set of features relevant for representing the pairs of protein sequences in a vector space model.
- Training. The set of preprocessed vectors characterizing pairs of proteins prepared at the previous stage will be used for training the AEs and for building the supervised learning model .
- Performance evaluation. This stage refers to the performance evaluation of our predictive model previously trained. will be tested on pairs of proteins unseen during the training stage and its performance will be assessed through relevant evaluation metrics.
3.2. Data Collection, Representation and Preprocessing
- 1.
- CT features [20] can be used to obtain fixed-length representations for protein sequences by grouping amino acids into seven classes based on their physico–chemical properties. Then, a sliding window of size 3 is passed through the protein sequence and the frequencies of possible triples of amino acid classes are computed. Thus, for a protein, a vector of size is built. Since longer protein sequences are more likely to have higher frequency values than shorter sequences, the final values of the CT descriptors are represented by the normalized frequencies. The CT descriptors were obtained using the iFeature library [31].
- 2.
- AC features are another type of descriptors which characterize variable-length protein sequences using vectors of fixed size [12]. Unlike CT features which take into account only groups of three consecutive amino acids, AC descriptors are able to capture long-term dependencies in a protein sequence, through defining a variable and computing correlations between amino acids situated in the sequence at at most positions apart. Thus, for m properties and a distance , a vector of size is obtained. We computed the AC features using the group of 14 amino acid properties provided by Chen et al. [15]. These properties are hydrophobicity computed using two different scales, hydrophilicity, net charge index of side chains, two scales of polarity, polarizability, solvent-accessible surface area, volume of side chains, flexibility, accessibility, exposed surface, turns scale and antegenic propensity [15]. Since the value of needs to be smaller than the sequence length, we selected different values, according to each tested data set (details are provided in Section 4).In the computation of both descriptors we used the default procedure of iFeature which removes non-standard amino-acids from the protein sequences.
3.3. Training
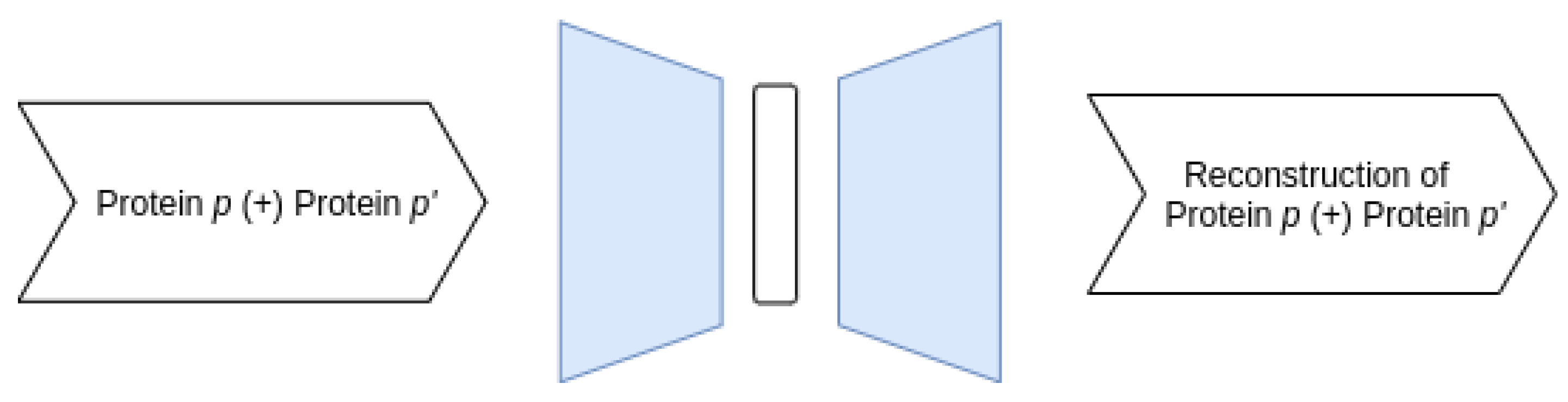
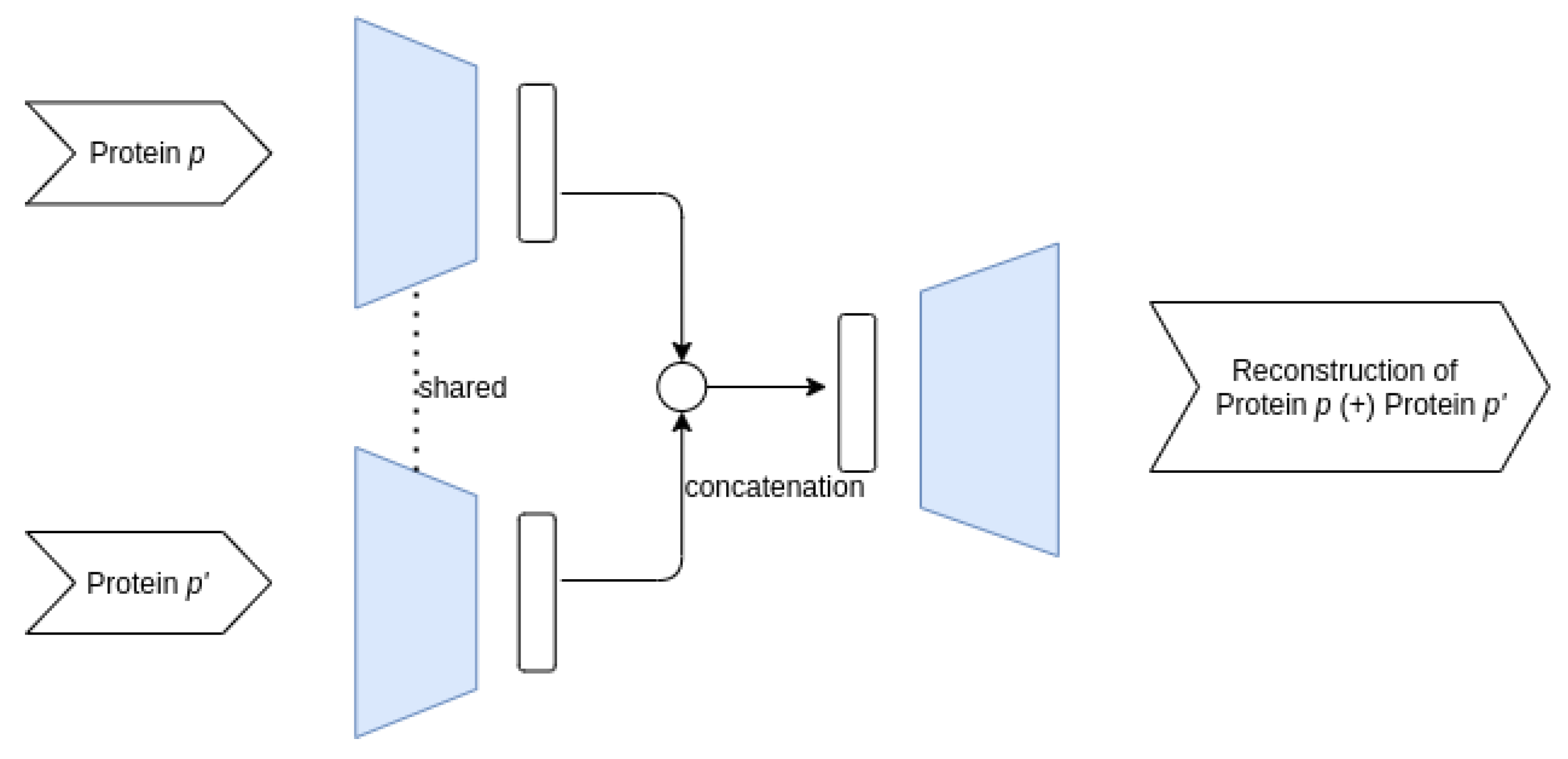
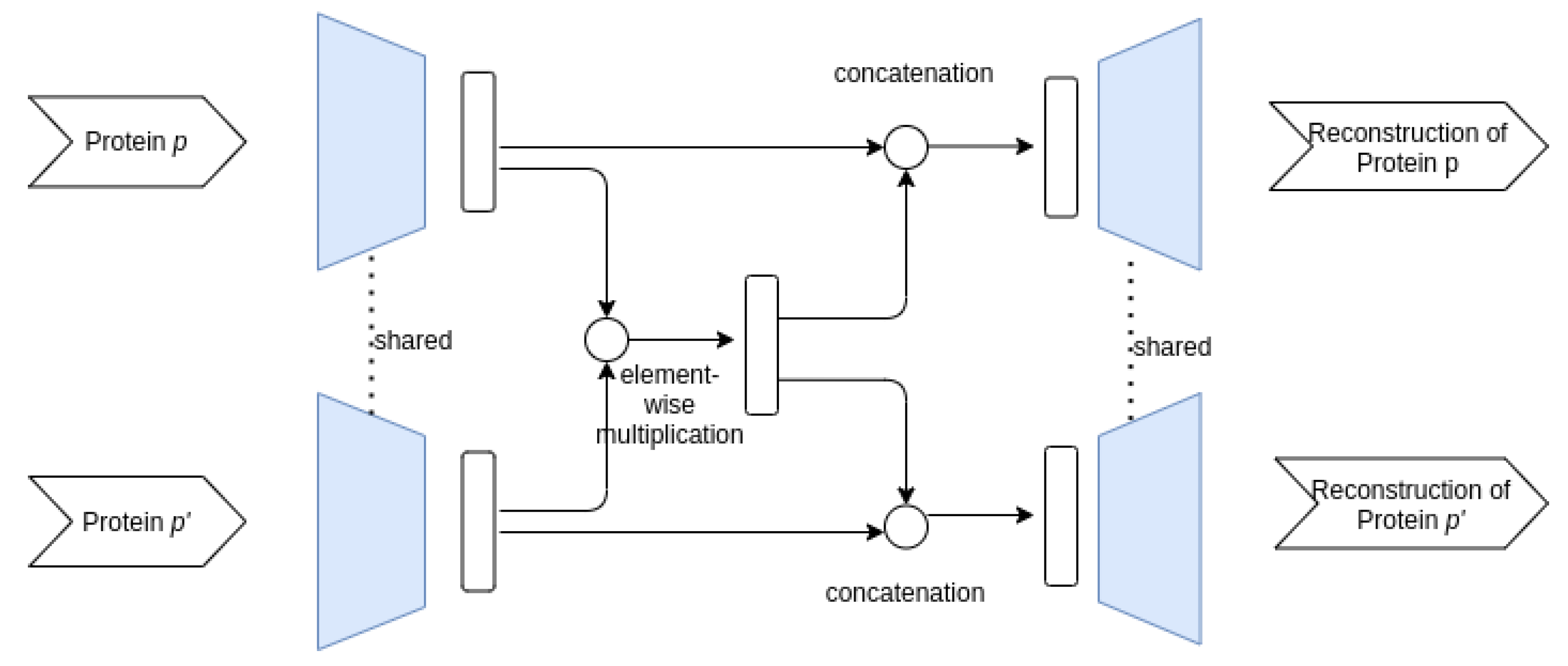
3.3.1. Proposed AE Architectures
- Joint–Joint architecture
- Siamese–Joint architecture
- Siamese–Siamese architecture
3.4. Performance Evaluation
3.4.1. Classification Using
3.4.2. Testing
- precision, ;
- recall or sensitivity, ;
- specificity or true negative rate, ;
- F1-score or F-score, ;
- Area Under the ROC Curve (), .
4. Experimental Results
4.1. Data Sets
4.2. Results
5. Comparison to Related Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, V.S.; Srinivas, K.; Sujini, G.; Kumar, G. Protein-protein interaction detection: Methods and analysis. Int. J. Proteom. 2014, 2014, 147648. [Google Scholar] [CrossRef]
- Prieto, D.A.; Johann, D.J., Jr.; Wei, B.R.; Ye, X.; Chan, K.C.; Nissley, D.V.; Simpson, R.M.; Citrin, D.E.; Mackall, C.L.; Linehan, W.M.; et al. Mass spectrometry in cancer biomarker research: A case for immunodepletion of abundant blood-derived proteins from clinical tissue specimens. Biomark. Med. 2014, 8, 269–286. [Google Scholar] [CrossRef]
- Von Mering, C.; Krause, R.; Snel, B.; Cornell, M.; Oliver, S.G.; Fields, S.; Bork, P. Comparative assessment of large-scale data sets of protein–protein interactions. Nature 2002, 417, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.C.; Petrey, D.; Deng, L.; Qiang, L.; Shi, Y.; Thu, C.A.; Bisikirska, B.; Lefebvre, C.; Accili, D.; Hunter, T.; et al. Structure-based prediction of protein–protein interactions on a genome-wide scale. Nature 2012, 490, 556–560. [Google Scholar] [CrossRef]
- Lee, S.A.; Chan, C.h.; Tsai, C.H.; Lai, J.M.; Wang, F.S.; Kao, C.Y.; Huang, C.Y.F. Ortholog-based protein-protein interaction prediction and its application to inter-species interactions. BMC Bioinform. 2008, 9, S11. [Google Scholar] [CrossRef]
- Planas-Iglesias, J.; Bonet, J.; García-García, J.; Marín-López, M.A.; Feliu, E.; Oliva, B. Understanding protein–protein interactions using local structural features. J. Mol. Biol. 2013, 425, 1210–1224. [Google Scholar] [CrossRef]
- Sun, T.; Zhou, B.; Lai, L.; Pei, J. Sequence-based prediction of protein protein interaction using a deep-learning algorithm. BMC Bioinform. 2017, 18, 277. [Google Scholar] [CrossRef]
- Sato, T.; Yamanishi, Y.; Kanehisa, M.; Horimoto, K.; Toh, H. Improvement of the mirrortree method by extracting evolutionary information. Insequence Genome Anal. Method Appl. 2011, 21, 129–139. [Google Scholar]
- Marcotte, E.M.; Pellegrini, M.; Ng, H.L.; Rice, D.W.; Yeates, T.O.; Eisenberg, D. Detecting protein function and protein-protein interactions from genome sequences. Science 1999, 285, 751–753. [Google Scholar] [CrossRef]
- Pesquita, C.; Faria, D.; Falcao, A.O.; Lord, P.; Couto, F.M. Semantic similarity in biomedical ontologies. PLoS Comput. Biol. 2009, 5, e1000443. [Google Scholar] [CrossRef] [PubMed]
- Jansen, R.; Yu, H.; Greenbaum, D.; Kluger, Y.; Krogan, N.J.; Chung, S.; Emili, A.; Snyder, M.; Greenblatt, J.F.; Gerstein, M. A Bayesian networks approach for predicting protein-protein interactions from genomic data. Science 2003, 302, 449–453. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, L.; Wen, Z.; Li, M. Using support vector machine combined with auto covariance to predict protein–protein interactions from protein sequences. Nucleic Acids Res. 2008, 36, 3025–3030. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.W.; Liu, M. Prediction of protein–protein interactions using random decision forest framework. Bioinformatics 2005, 21, 4394–4400. [Google Scholar] [CrossRef]
- Browne, F.; Wang, H.; Zheng, H.; Azuaje, F. Supervised statistical and machine learning approaches to inferring pairwise and module-based protein interaction networks. In Proceedings of the 2007 IEEE 7th International Symposium on BioInformatics and BioEngineering, Boston, MA, USA, 14–17 October 2007; pp. 1365–1369. [Google Scholar]
- Chen, K.H.; Wang, T.F.; Hu, Y.J. Protein-protein interaction prediction using a hybrid feature representation and a stacked generalization scheme. BMC Bioinform. 2019, 20, 308. [Google Scholar] [CrossRef]
- Bagheri, H.; Dyer, R.; Severin, A.; Rajan, H. Comprehensive Analysis of Non Redundant Protein Database. Res. Sq. 2020. Available online: https://www.researchsquare.com/article/rs-54568/v1 (accessed on 20 May 2021).
- Levitt, M. Nature of the protein universe. Proc. Natl. Acad. Sci. USA 2009, 106, 11079–11084. [Google Scholar] [CrossRef]
- PDB Statistics: Overall Growth of Released Structures Per Year. Available online: https://www.rcsb.org/stats/growth/growth-released-structures (accessed on 18 March 2021).
- Chen, M.; Ju, C.J.T.; Zhou, G.; Chen, X.; Zhang, T.; Chang, K.W.; Zaniolo, C.; Wang, W. Multifaceted protein–protein interaction prediction based on Siamese residual RCNN. Bioinformatics 2019, 35, i305–i314. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Luo, X.; Zhu, W.; Yu, K.; Chen, K.; Li, Y.; Jiang, H. Predicting protein–protein interactions based only on sequences information. Proc. Natl. Acad. Sci. USA 2007, 104, 4337–4341. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhu, F.; Ling, X.; Liu, Q. Protein Interaction Network Reconstruction Through Ensemble Deep Learning With Attention Mechanism. Front. Bioeng. Biotechnol. 2020, 8, 839. [Google Scholar] [CrossRef]
- Wang, Y.B.; You, Z.H.; Li, X.; Jiang, T.H.; Chen, X.; Zhou, X.; Wang, L. Predicting protein–protein interactions from protein sequences by a stacked sparse autoencoder deep neural network. Mol. Biosyst. 2017, 13, 1336–1344. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; You, Z.; Li, L.; Cheng, L.; Zhou, X.; Zhang, L.; Li, X.; Jiang, T. Predicting protein interactions using a deep learning method-stacked sparse autoencoder combined with a probabilistic classification vector machine. Complexity 2018, 2018, 4216813. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, B. AE-LGBM: Sequence-based novel approach to detect interacting protein pairs via ensemble of autoencoder and LightGBM. Comput. Biol. Med. 2020, 125, 103964. [Google Scholar] [CrossRef]
- Yang, F.; Fan, K.; Song, D.; Lin, H. Graph-based prediction of Protein-protein interactions with attributed signed graph embedding. BMC Bioinform. 2020, 21, 323. [Google Scholar] [CrossRef] [PubMed]
- Alain, G.; Bengio, Y. What regularized auto-encoders learn from the data-generating distribution. J. Mach. Learn. Res. 2014, 15, 3563–3593. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese Neural Networks for One-Shot Image Recognition. 2015. Available online: https://www.cs.cmu.edu/~rsalakhu/papers/oneshot1.pdf (accessed on 21 May 2021).
- Deudon, M. Learning semantic similarity in a continuous space. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31, pp. 986–997. [Google Scholar]
- Utkin, L.V.; Zaborovsky, V.S.; Lukashin, A.A.; Popov, S.G.; Podolskaja, A.V. A siamese autoencoder preserving distances for anomaly detection in multi-robot systems. In Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), Prague, Czech Republic, 20–22 May 2017; pp. 39–44. [Google Scholar]
- You, Z.H.; Lei, Y.K.; Zhu, L.; Xia, J.; Wang, B. Prediction of protein-protein interactions from amino acid sequences with ensemble extreme learning machines and principal component analysis. In BMC Bioinformatics; Springer: Berlin, Germany, 2013; Volume 14, pp. 1–11. [Google Scholar]
- Chen, Z.; Zhao, P.; Li, F.; Leier, A.; Marquez-Lago, T.T.; Wang, Y.; Webb, G.I.; Smith, A.I.; Daly, R.J.; Chou, K.C.; et al. iFeature: A python package and web server for features extraction and selection from protein and peptide sequences. Bioinformatics 2018, 34, 2499–2502. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Hu, Y.; Cheng, L. Conjoint Feature Representation of GO and Protein Sequence for PPI Prediction Based on an Inception RNN Attention Network. Mol. Ther. Nucleic Acids 2020, 22, 198–208. [Google Scholar] [CrossRef]
- Li, H.; Gong, X.J.; Yu, H.; Zhou, C. Deep neural network based predictions of protein interactions using primary sequences. Molecules 2018, 23, 1923. [Google Scholar] [CrossRef]
- Hashemifar, S.; Neyshabur, B.; Khan, A.A.; Xu, J. Predicting protein–protein interactions through sequence-based deep learning. Bioinformatics 2018, 34, i802–i810. [Google Scholar] [CrossRef]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. arXiv 2017, arXiv:1706.02515. [Google Scholar]
- Abadi, M. TensorFlow: Learning functions at scale. In Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, Nara, Japan, 18–24 September 2016; ACM: New York, NY, USA, 2016; p. 1. [Google Scholar]
- Gu, Q.; Zhu, L.; Cai, Z. Evaluation Measures of the Classification Performance of Imbalanced Data Sets. In Proceedings of the International Symposium on Intelligence Computation and Applications (ISICA), Huangshi, China, 23–25 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 461–471. [Google Scholar]
- Brown, L.; Cat, T.; DasGupta, A. Interval Estimation for a proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar] [CrossRef]
- Pan, X.Y.; Zhang, Y.N.; Shen, H.B. Large-Scale prediction of human protein- protein interactions from amino acid sequence based on latent topic features. J. Proteome Res. 2010, 9, 4992–5001. [Google Scholar] [CrossRef]
- Guo, Y.; Li, M.; Pu, X.; Li, G.; Guang, X.; Xiong, W.; Li, J. PRED_PPI: A server for predicting protein-protein interactions based on sequence data with probability assignment. Bmc Res. Notes 2010, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Nanni, L.; Lumini, A.; Brahnam, S. An empirical study on the matrix-based protein representations and their combination with sequence-based approaches. Amino Acids 2013, 44, 887–901. [Google Scholar] [CrossRef] [PubMed]
- You, Z.H.; Yu, J.Z.; Zhu, L.; Li, S.; Wen, Z.K. A MapReduce based parallel SVM for large-scale predicting protein–protein interactions. Neurocomputing 2014, 145, 37–43. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Pan, X.Y.; Huang, Y.; Shen, H.B. Adaptive compressive learning for prediction of protein–protein interactions from primary sequence. J. Theor. Biol. 2011, 283, 44–52. [Google Scholar] [CrossRef]
- You, Z.H.; Li, S.; Gao, X.; Luo, X.; Ji, Z. Large-scale protein-protein interactions detection by integrating big biosensing data with computational model. Biomed Res. Int. 2014, 2014, 598129. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, R.; Wei, Y.; Wang, X. DNN-PPI: A Large-Scale Prediction of Protein–Protein Interactions Based on Deep Neural Networks. J. Biol. Syst. 2019, 27, 1–18. [Google Scholar] [CrossRef]
- Gui, Y.M.; Wang, R.J.; Wang, X.; Wei, Y.Y. Using deep neural networks to improve the performance of protein-protein interactions prediction. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2052012. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Wei, Y.; Gui, Y. A novel conjoint triad auto covariance (CTAC) coding method for predicting protein-protein interaction based on amino acid sequence. Math. Biosci. 2019, 313, 41–47. [Google Scholar] [CrossRef]
- Siegel, S.; Castellan, N. Nonparametric Statistics for the Behavioral Sciences, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Social Science Statistics. Available online: http://www.socscistatistics.com/tests/ (accessed on 20 May 2021).
| Data Set | Number of Positive Interactions | Number of Negative Interactions |
|---|---|---|
| HPRD | 36,630 | 36,480 |
| Multi-species | 32,959 | 32,959 |
| Multi-species < 0.25 | 19,458 | 15,827 |
| Multi-species < 0.01 | 10,747 | 8065 |
| Data Set | Arch. | Accuracy | Precision | Recall | Specificity | AUC | |
|---|---|---|---|---|---|---|---|
| HPRD | 1 | 0.977 ± 0.0006 | 0.977 ± 0.0007 | 0.986 ± 0.0009 | 0.968 ± 0.001 | 0.986 ± 0.0009 | 0.977 ± 0.0006 |
| 2 | 0.979 ± 0.0007 | 0.979 ± 0.0007 | 0.973 ± 0.0015 | 0.985 ± 0.009 | 0.973 ± 0.0015 | 0.979 ± 0.0007 | |
| 3 | 0.96 ± 0.0014 | 0.959 ± 0.0015 | 0.992 ± 0.006 | 0.928 ± 0.0024 | 0.992 ± 0.006 | 0.960 ± 0.0014 | |
| Multi-species | 1 | 0.97 ± 0.0007 | 0.969 ± 0.0006 | 0.995 ± 0.0007 | 0.944 ± 0.0015 | 0.995 ± 0.0006 | 0.97 ± 0.0005 |
| 2 | 0.969 ± 0.0008 | 0.97 ± 0.0009 | 0.965 ± 0.0028 | 0.974 ± 0.002 | 0.964 ± 0.0025 | 0.97 ± 0.008 | |
| 3 | 0.982 ± 0.0008 | 0.982 ± 0.0008 | 1 ± 0 | 0.964 ± 0.0016 | 1 ± 0 | 0.982 ± 0.008 | |
| Multi-species <0.25 | 1 | 0.973 ± 0.0011 | 0.975 ± 0.0009 | 0.995 ± 0.0011 | 0.956 ± 0.0017 | 0.995 ± 0.0012 | 0.975 ± 0.001 |
| 2 | 0.976 ± 0.0007 | 0.978 ± 0.0008 | 0.974 ± 0.0011 | 0.983 ± 0.0008 | 0.968 ± 0.0013 | 0.975 ± 0.0008 | |
| 3 | 0.983 ± 0.0015 | 0.984 ± 0.0014 | 1 ± 0 | 0.969 ± 0.0027 | 1 ± 0 | 0.985 ± 0.0013 | |
| Multi-species <0.01 | 1 | 0.972 ± 0.0023 | 0.975 ± 0.0019 | 0.993 ± 0.001 | 0.958 ± 0.0035 | 0.991 ± 0.0015 | 0.975 ± 0.002 |
| 2 | 0.978 ± 0.0015 | 0.981 ± 0.0013 | 0.975 ± 0.0024 | 0.987 ± 0.0027 | 0.966 ± 0.0031 | 0.976 ± 0.0015 | |
| 3 | 0.981 ± 0.0016 | 0.983 ± 0.0014 | 1 ± 0 | 0.966 ± 0.0027 | 1 ± 0 | 0.983 ± 0.0014 |
| Method | Accuracy | F1 |
|---|---|---|
| 0.979 ± 0.0007 | 0.979 ± 0.0007 | |
| SAE [7] | 0.9719 | - |
| PIPR [19] | 0.9811 | 0.9803 |
| LDA-RF [39] | 0.979 ± 0.005 | - |
| CT-SVM [20] reported in [7] | 0.83 | - |
| AC-SVM [40] reported in [7] | 0.9037 | - |
| Parallel SVM [42] reported in [7] | 0.9200–0.9740 | - |
| ELM [44] reported in [7] | 0.8480 | 0.8477 |
| CS-SVM [43] | 0.941 | 0.937 |
| SVM [41] | 0.942 | - |
| DNN [46] | 0.9443 ± 0.0036 | - |
| DNN-PPI [45] | 0.9726 ± 0.0018 | - |
| DNN-CTAC [47] | 0.9837 | - |
| S-VGAE [25] | 0.9915 ± 0.0011 | 0.9915 ± 0.0012 |
| Data Set | Method | Accuracy | F1 |
|---|---|---|---|
| Multi-species | 0.9821± 0.0008 | 0.9818 ± 0.0008 | |
| PIPR [19] | 0.9819 | 0.9817 | |
| Multi-species <0.25 | 0.9829 ± 0.0015 | 0.9842 ± 0.0014 | |
| PIPR [19] | 0.9791 | 0.9808 | |
| Multi-species <0.01 | 0.9808 ± 0.0016 | 0.9829 ± 0.0014 | |
| PIPR [19] | 0.9751 | 0.9780 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czibula, G.; Albu, A.-I.; Bocicor, M.I.; Chira, C. AutoPPI: An Ensemble of Deep Autoencoders for Protein–Protein Interaction Prediction. Entropy 2021, 23, 643. https://doi.org/10.3390/e23060643
Czibula G, Albu A-I, Bocicor MI, Chira C. AutoPPI: An Ensemble of Deep Autoencoders for Protein–Protein Interaction Prediction. Entropy. 2021; 23(6):643. https://doi.org/10.3390/e23060643
Chicago/Turabian StyleCzibula, Gabriela, Alexandra-Ioana Albu, Maria Iuliana Bocicor, and Camelia Chira. 2021. "AutoPPI: An Ensemble of Deep Autoencoders for Protein–Protein Interaction Prediction" Entropy 23, no. 6: 643. https://doi.org/10.3390/e23060643
APA StyleCzibula, G., Albu, A.-I., Bocicor, M. I., & Chira, C. (2021). AutoPPI: An Ensemble of Deep Autoencoders for Protein–Protein Interaction Prediction. Entropy, 23(6), 643. https://doi.org/10.3390/e23060643





