Multiple Observations for Secret-Key Binding with SRAM PUFs
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions and Outline
- We introduce the MO helper data scheme in Section 4. We prove that the helper data does not reveal any information about the key when the SRAM-PUF statistical model meets the symmetry assumption (Section 2). Then, we prove that secret-key capacity can be achieved with the MO helper data scheme for any number of enrollment observations.
- In Section 5, we present a code construction and evaluate performance of the scheme through Monte Carlo simulations.
- We propose a new variation on the Soft-Decision (SD) helper data scheme from [7] in Section 6. In contrast to the original scheme, this scheme considers binary SRAM-PUF observations as an input. We prove that the new SD strategy is optimal (achieves secret-key capacity) and that it can achieve the same reconstruction performance as the MO helper data scheme.
- In Section 7, we present a variation on the MO helper data scheme that can update the helper data sequentially. The error-correcting performance of the scheme improves after each successful key reconstruction, and therefore the performance improves over the lifetime of the device. This enables usage of less observations during the enrollment phase, when allowing worse initial reconstruction performance that is improved over time.
2. Notation and SRAM-PUF Statistical Model
2.1. Notation and Definitions
2.2. Sram-Puf Statistical Model
2.2.1. One-Probability of a Cell
2.2.2. Multiple Observations
2.2.3. Multiple SRAM Cells
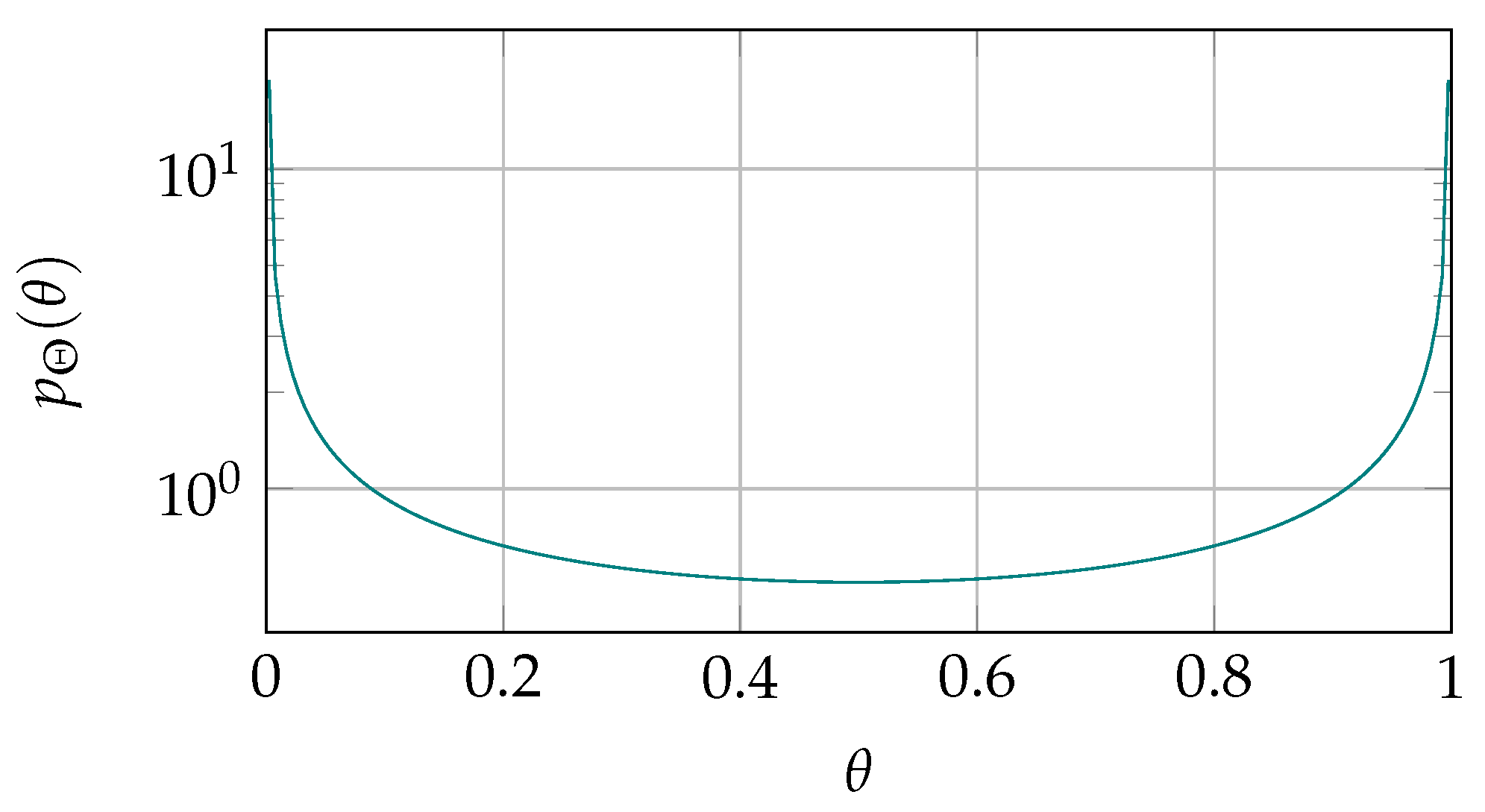
2.2.4. -Distribution
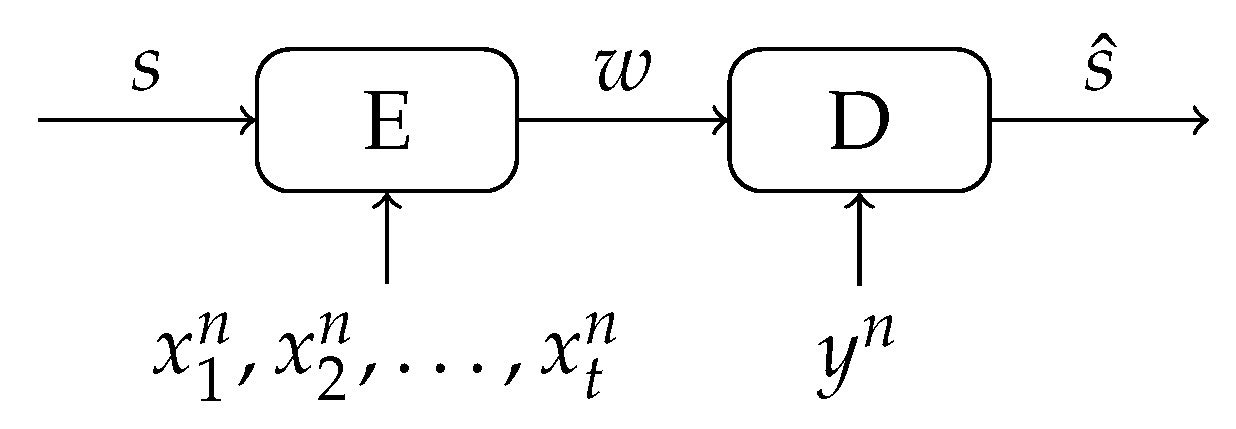
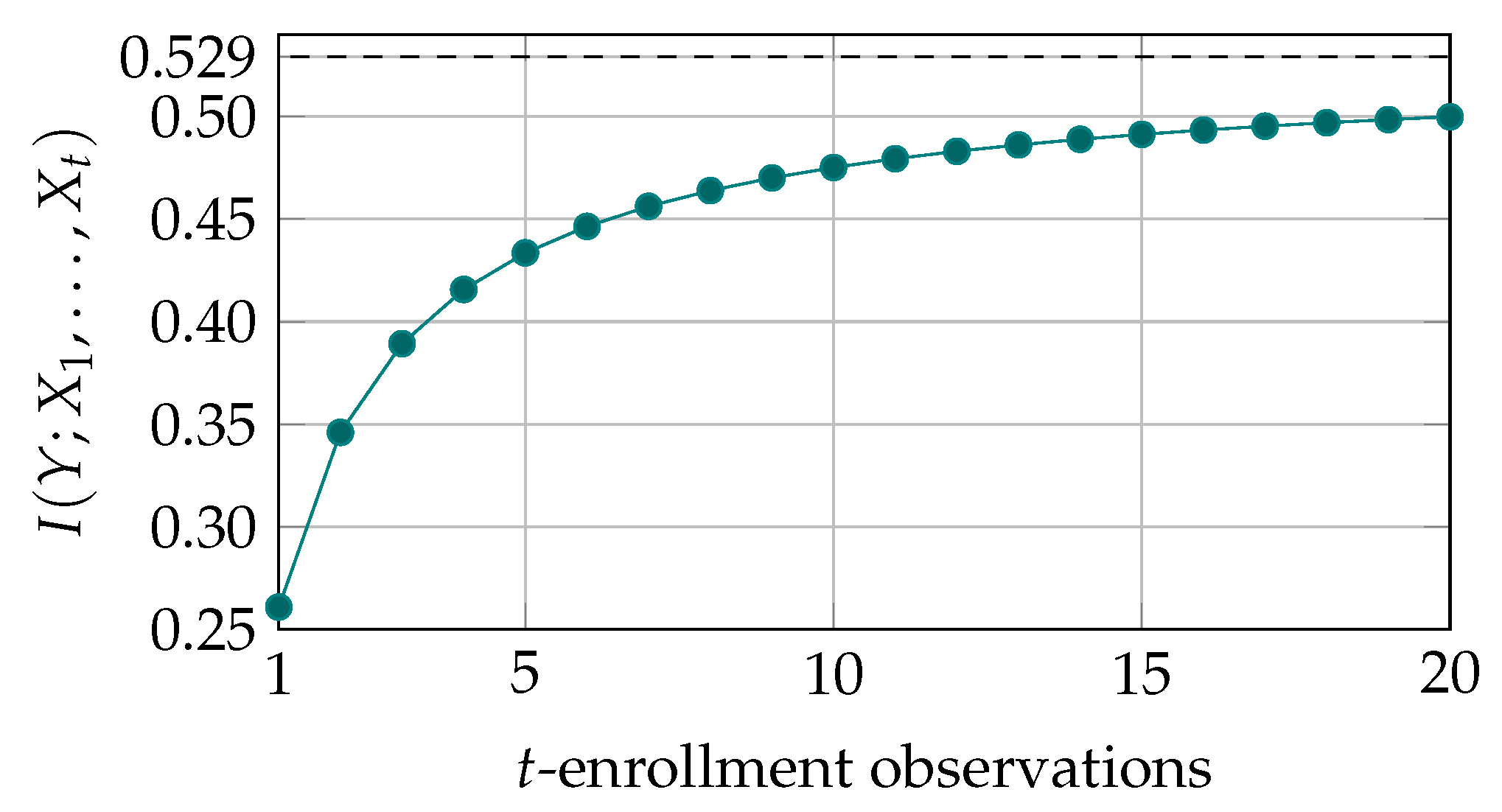
3. Multiple Enrollment Observations for Increased Secret-Key Capacity
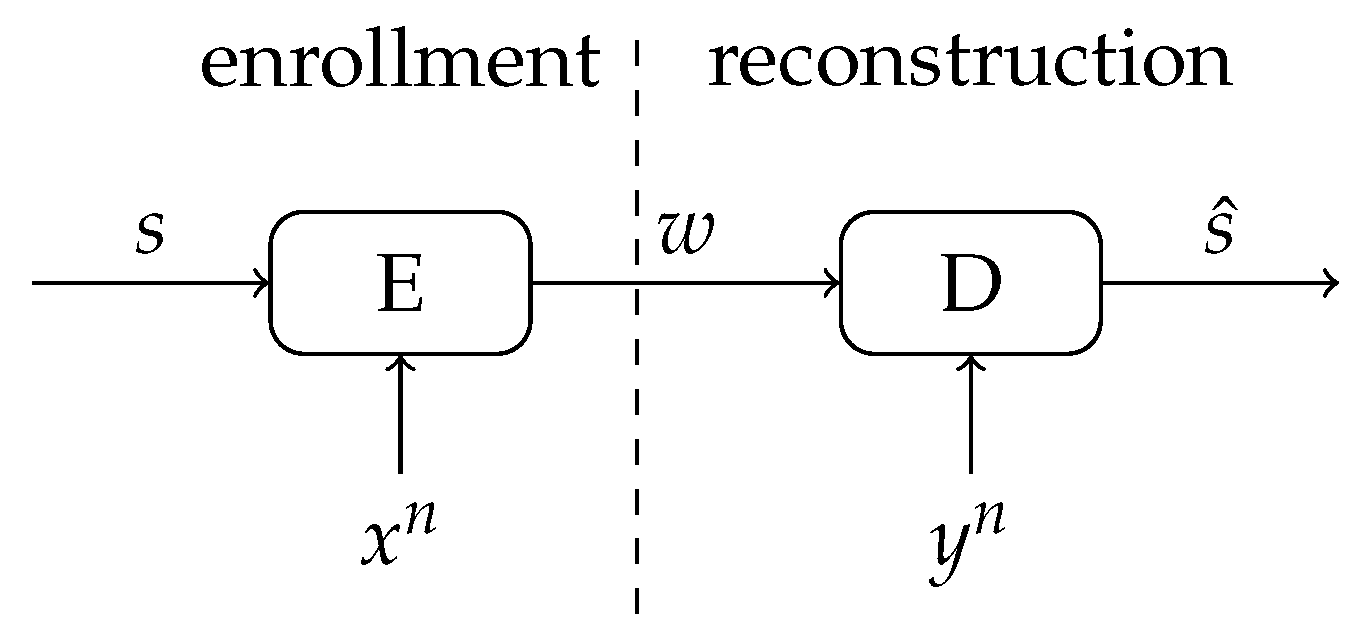
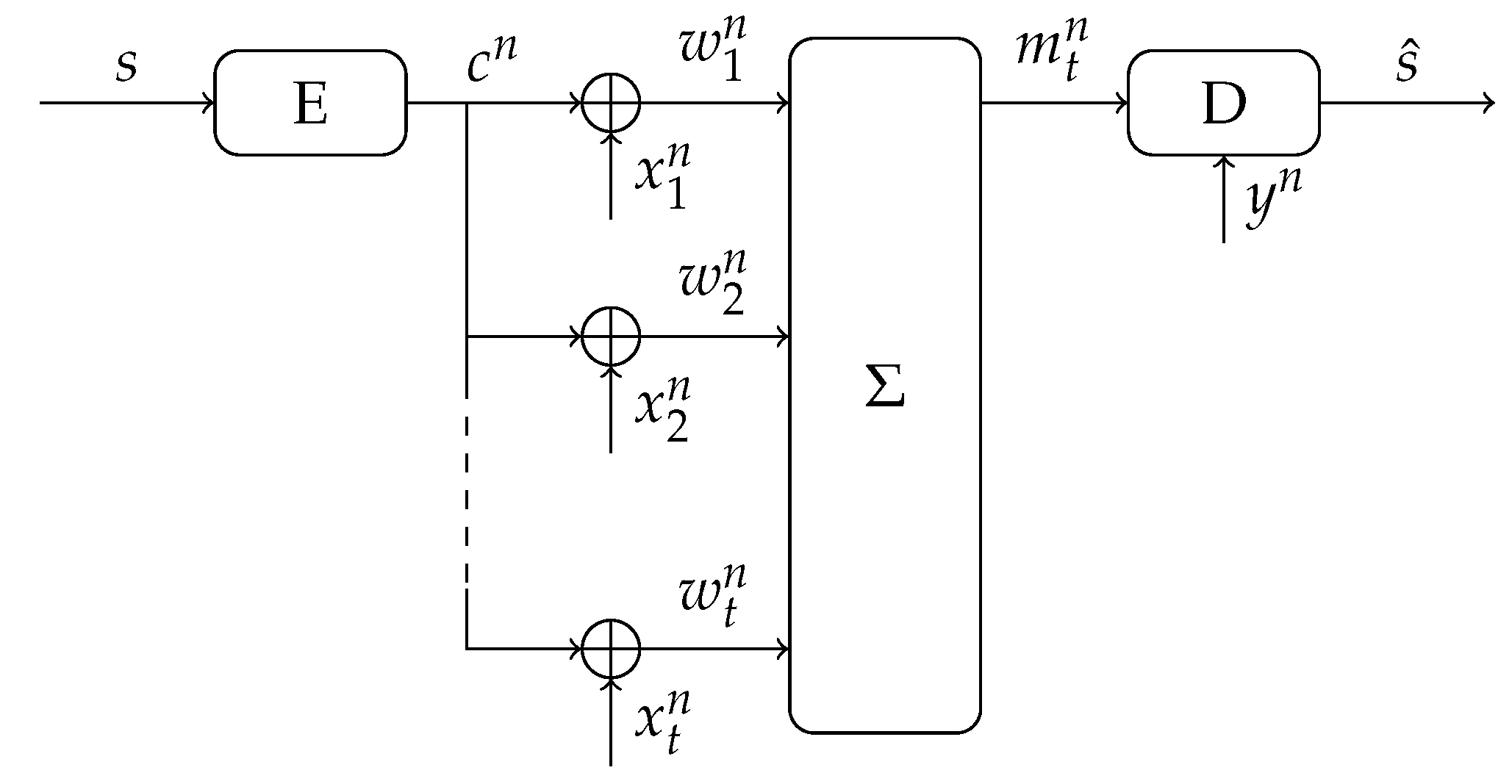
4. Multiple-Observations Helper Data Scheme
4.1. Description of the Scheme
4.2. Uniformity and Zero Leakage
4.3. Achievable Secret-Key Rate
5. Code Construction and Simulation Results
5.1. Encoder
5.2. Decoder
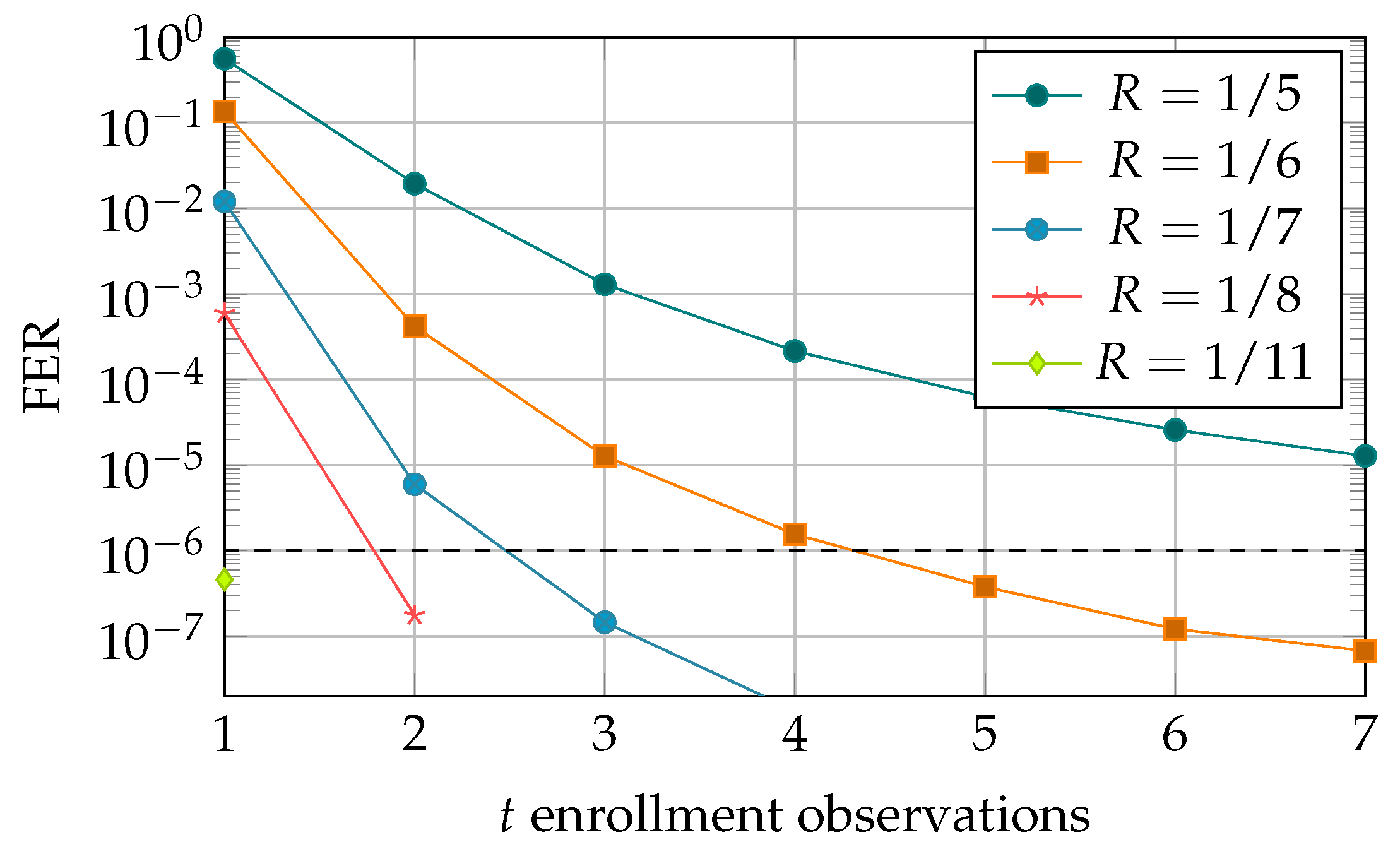
5.3. Simulation Results
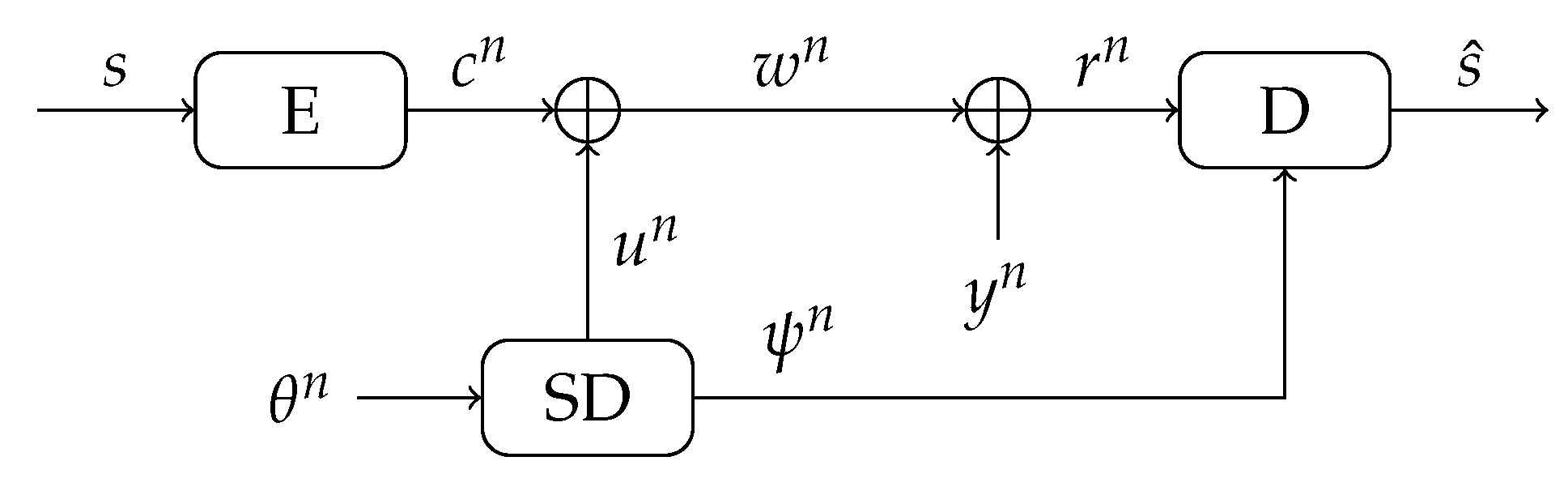
6. The Soft-Decision Helper Data Scheme
6.1. Description of (Regular) SD Helper Data Scheme
6.2. Achievable Performance
6.3. New SD Strategy for Binary Enrollment Observations
6.4. Achievable Performance
6.5. Code Construction and Simulations
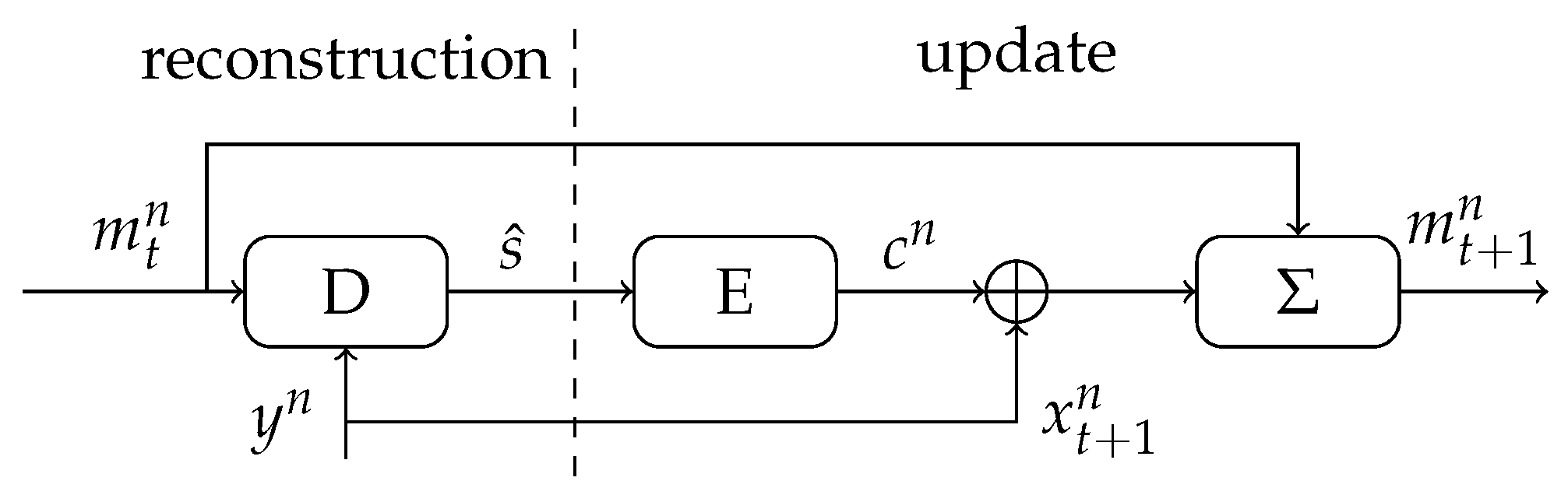
7. Sequential MO Helper Data Scheme
7.1. Description
7.2. Security and Achievable Rate
7.3. Simulation Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SRAM | Static Random-Access Memory |
| PUF | Physical Unclonable Function |
| MO | Multiple Observations |
| SMO | Sequential Multiple Observations |
| SD | Soft Decision |
| LDPC | Low-density Parity-check |
| LLR | Log-likelihood ratio |
| CRC | cyclic-redundancy check |
Appendix A.
Appendix A.1. Log-Likelihood Ratio for MO Helper Data Scheme
Appendix A.2. Zero Leakage Proof for Traditional SD Helper Data Scheme
Appendix A.3. Reliability Estimate for Binary SD Helper Data Scheme
Appendix A.4. Zero Leakage Proof for Binary SD Helper Data Scheme
Appendix A.5. Log-Likelihood Ratio for Binary SD Helper Data Scheme
References
- Pappu, R.; Recht, B.; Taylor, J.; Gershenfeld, N. Physical One-Way Functions. Science 2002, 297, 2026–2030. [Google Scholar] [CrossRef] [PubMed]
- Gassend, B.; Clarke, D.; van Dijk, M.; Devadas, S. Silicon physical random functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security—CCS, Washington, DC, USA, 18–22 November 2002. [Google Scholar] [CrossRef]
- Holcomb, D.E.; Burleson, W.P.; Fu, K. Power-Up SRAM state as an identifying fingerprint and source of true random numbers. IEEE Trans. Comput. 2009, 58, 1198–1210. [Google Scholar] [CrossRef]
- Guajardo, J.; Kumar, S.S.; Schrijen, G.J.; Tuyls, P. FPGA Intrinsic PUFs and Their Use for IP Protection. In Cryptographic Hardware Embedded System—CHES; Springer: Berlin/Heidelberg, Germany, 2007; pp. 63–80. [Google Scholar]
- van den Berg, R.; Škorić, B.; van der Leest, V. Bias-based modeling and entropy analysis of PUFs. In Proceedings of the 3rd Int. Workshop Trustworthy Embedded Devices—TrustED, Berlin, Germany, 4 November 2013; pp. 13–20. [Google Scholar] [CrossRef]
- Juels, A.; Wattenberg, M. A fuzzy commitment scheme. In Proceedings of the 6th ACM Conference on Computer and Communications Security—CCS, Singapore, 1–4 November 1999; pp. 28–36. [Google Scholar] [CrossRef]
- Maes, R.; Tuyls, P.; Verbauwhede, I. A soft decision helper data algorithm for SRAM PUFs. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 2101–2105. [Google Scholar] [CrossRef]
- Maes, R.; Tuyls, P.; Verbauwhede, I. Low-Overhead Implementation of a Soft Decision Helper Data Algorithm for SRAM PUFs. In Cryptographic Hardware and Embedded System—CHES; Springer: Berlin/Heidelberg, Germany, 2009; pp. 332–347. [Google Scholar] [CrossRef]
- Yu, M.D.; Devadas, S. Secure and robust error correction for physical unclonable functions. IEEE Des. Test Comput. 2010, 27, 48–65. [Google Scholar] [CrossRef]
- Hiller, M.; Merli, D.; Stumpf, F.; Sigl, G. Complementary IBS: Application specific error correction for PUFs. In Proceedings of the 2012 IEEE International Symposium on Hardware-Oriented Security and Trust, San Francisco, CA, USA, 3–4 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Hiller, M.; Yu, M.D.M.; Sigl, G. Cherry-Picking Reliable PUF Bits with Differential Sequence Coding. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2065–2076. [Google Scholar] [CrossRef]
- Gao, Y.; Su, Y.; Xu, L.; Ranasinghe, D.C. Lightweight (Reverse) Fuzzy Extractor With Multiple Reference PUF Responses. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1887–1901. [Google Scholar] [CrossRef]
- Günlü, O.; Kramer, G. Privacy, Secrecy, and Storage with Multiple Noisy Measurements of Identifiers. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2872–2883. [Google Scholar] [CrossRef]
- Günlü, O. Multi-Entity and Multi-Enrollment Key Agreement With Correlated Noise. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1190–1202. [Google Scholar] [CrossRef]
- Kusters, L.; Willems, F.M.J. Secret-Key Capacity Regions for Multiple Enrollments With an SRAM-PUF. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2276–2287. [Google Scholar] [CrossRef]
- Boyen, X. Reusable cryptographic fuzzy extractors. In Proceedings of the 11th ACM Conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 82–91. [Google Scholar]
- Kusters, L.; Ignatenko, T.; Willems, F.M.J.; Maes, R.; van der Sluis, E.; Selimis, G. Security of helper data schemes for SRAM-PUF in multiple enrollment scenarios. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1803–1807. [Google Scholar] [CrossRef]
- Van Herrewege, A.; Katzenbeisser, S.; Maes, R.; Peeters, R.; Sadeghi, A.R.; Verbauwhede, I.; Wachsmann, C. Reverse fuzzy extractors: Enabling lightweight mutual authentication for PUF-enabled RFIDs. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kralendijk, Bonaire, 27 Februray–2 March 2012; Volume 7397 LNCS, pp. 374–389. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Katzenbeisser, S.; Kocabaş, Ü.; Rožić, V.; Sadeghi, A.R.; Verbauwhede, I.; Wachsmann, C. PUFs: Myth, Fact or Busted? A Security Evaluation of Physically Unclonable Functions (PUFs) Cast in Silicon. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Leuven, Belgium, 9–12 September 2012; pp. 283–301. [Google Scholar]
- Maes, R. An Accurate Probabilistic Reliability Model for Silicon PUFs. In Proceedings of the International Conference on Cryptographic Hardware and Embedded Systems, Santa Barbara, CA, USA, 19–22 August 2015; pp. 73–89. [Google Scholar] [CrossRef]
- Kusters, L.; Rikos, A.; Willems, F.M.J. Modeling Temperature Behavior in the Helper Data for Secret-Key Binding with SRAM PUFs. In Proceedings of the 2020 IEEE Conference on Communications and Network Security (CNS), Avignon, France, 29 June–1 July 2020. [Google Scholar]
- Ahlswede, R.; Csiszàr, I. Common Randomness in Information Theory & Cryptography. IEEE Trans. Inf. Theory 1993, 39, 1121–1132. [Google Scholar]
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Hui, D.; Sandberg, S.; Blankenship, Y.; Andersson, M.; Grosjean, L. Channel Coding in 5G New Radio: A Tutorial Overview and Performance Comparison with 4G LTE. IEEE Veh. Technol. Mag. 2018, 13, 60–69. [Google Scholar] [CrossRef]
- MATLAB and 5G Toolbox Release; The MathWorks, Inc.: Natick, MA, USA, 2020.
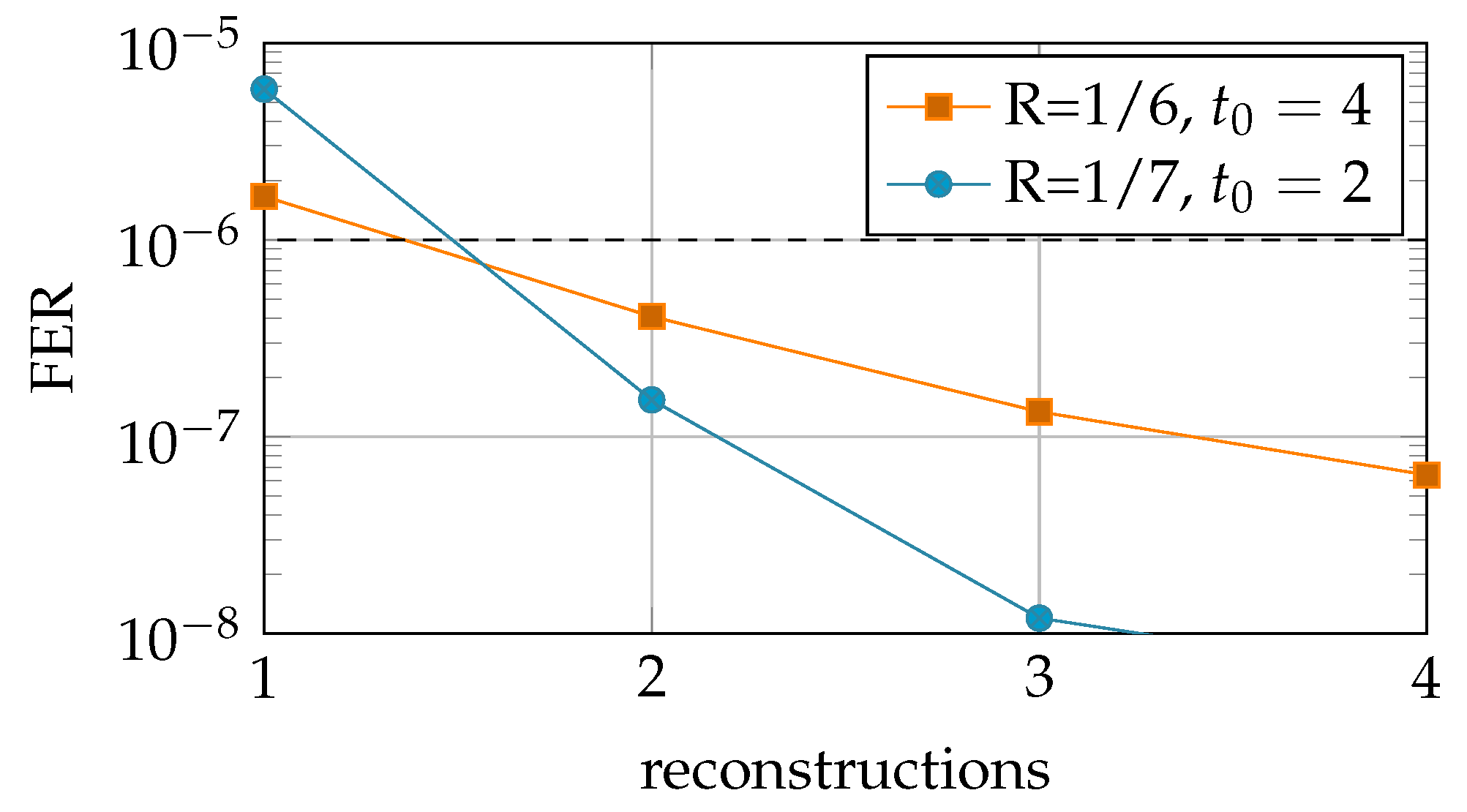
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusters, L.; Willems, F.M.J. Multiple Observations for Secret-Key Binding with SRAM PUFs. Entropy 2021, 23, 590. https://doi.org/10.3390/e23050590
Kusters L, Willems FMJ. Multiple Observations for Secret-Key Binding with SRAM PUFs. Entropy. 2021; 23(5):590. https://doi.org/10.3390/e23050590
Chicago/Turabian StyleKusters, Lieneke, and Frans M. J. Willems. 2021. "Multiple Observations for Secret-Key Binding with SRAM PUFs" Entropy 23, no. 5: 590. https://doi.org/10.3390/e23050590
APA StyleKusters, L., & Willems, F. M. J. (2021). Multiple Observations for Secret-Key Binding with SRAM PUFs. Entropy, 23(5), 590. https://doi.org/10.3390/e23050590





