Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy
Abstract
1. Introduction
2. Preliminaries
2.1. Shannon Entropy
2.2. Comparison Criterion between the Estimators of H
3. Entropy Estimators
3.1. Theoretical Approximations between Estimators of Entropy
3.2. Previous Work on Comparison of Entropy Estimators
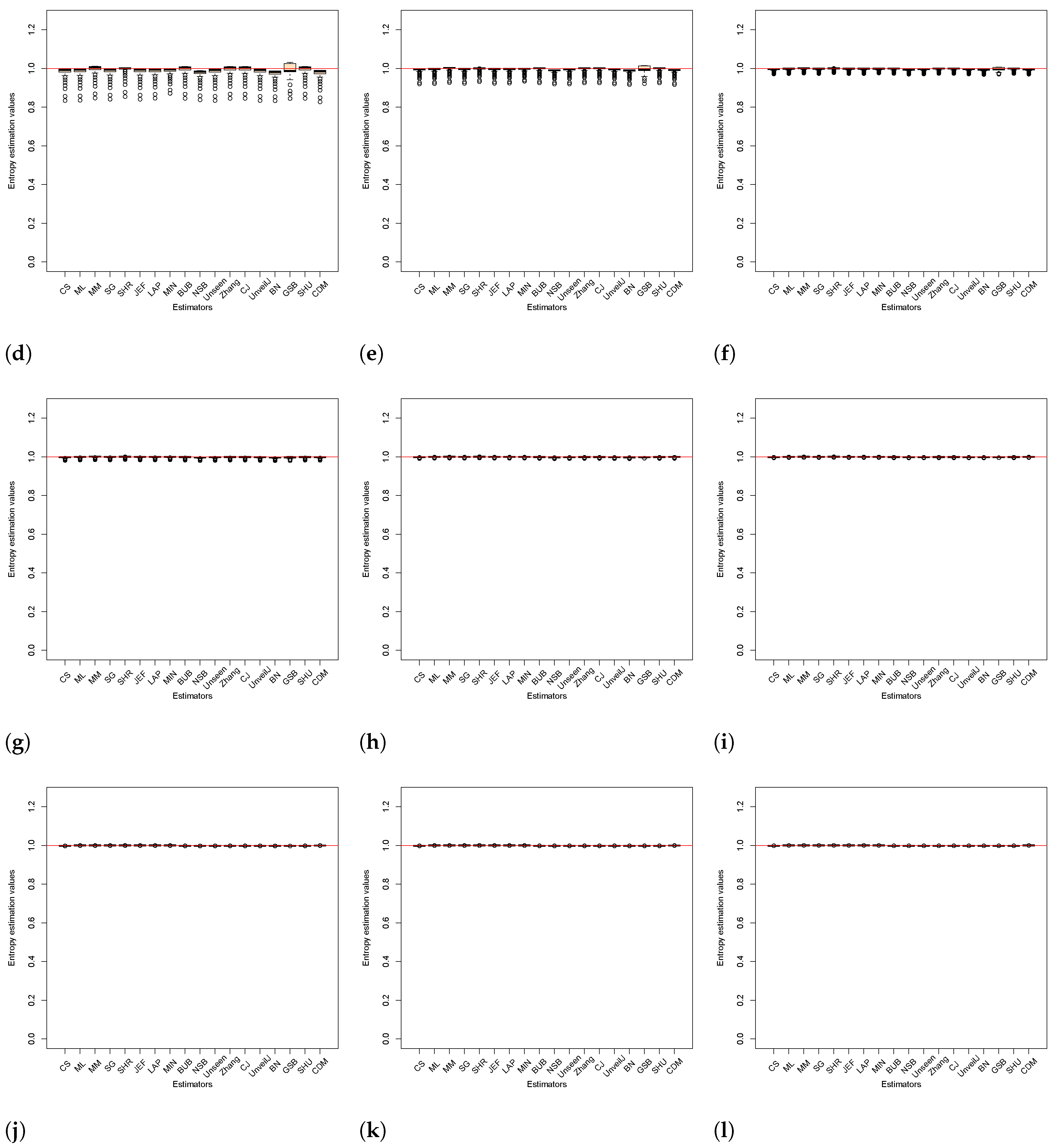
4. Selecting an Effective Entropy Estimator through Experimental Evaluation
4.1. Implementation of Entropy Estimators
4.2. Analysis of Bias between Estimators
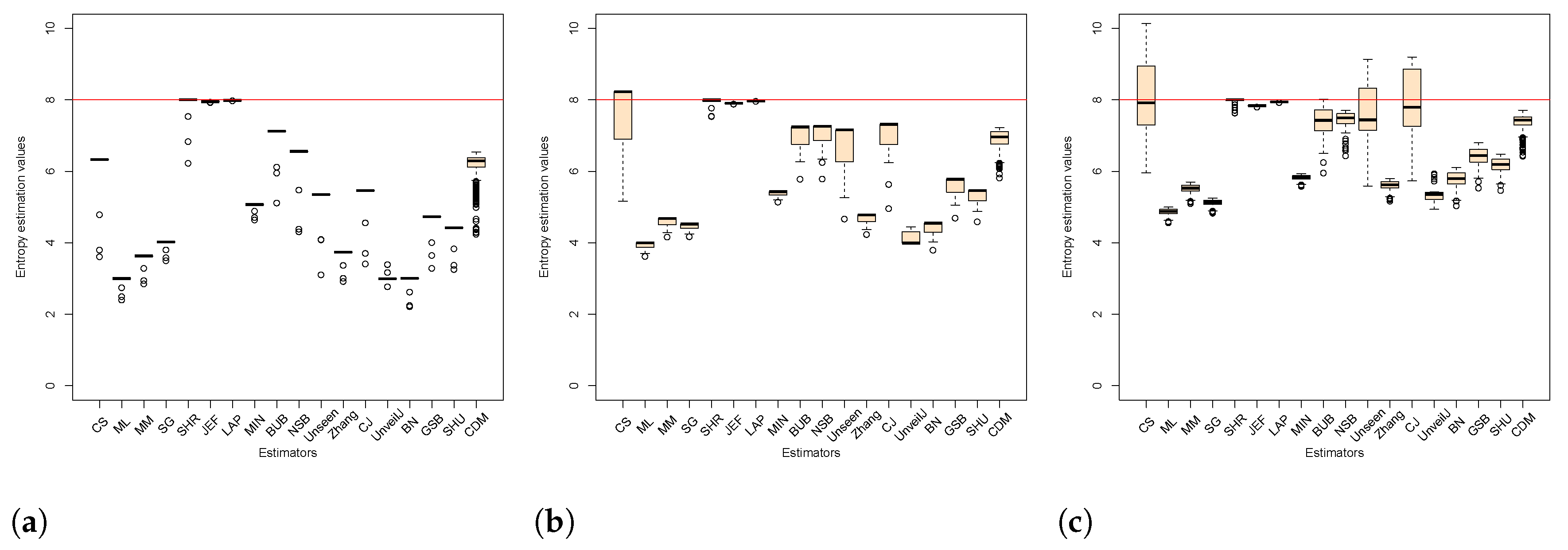
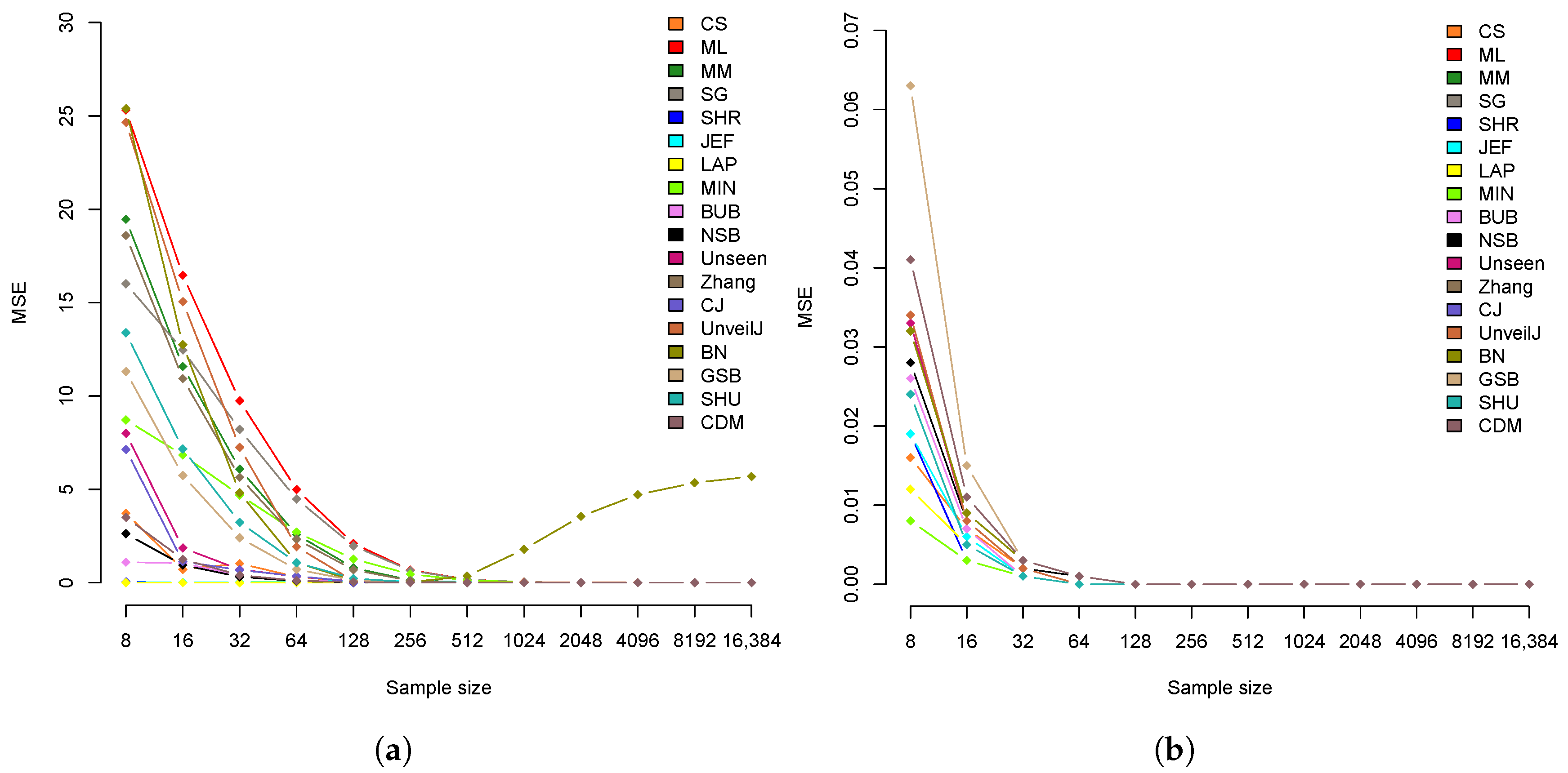
4.3. Comparison of Estimators in Terms of Mean Square Error
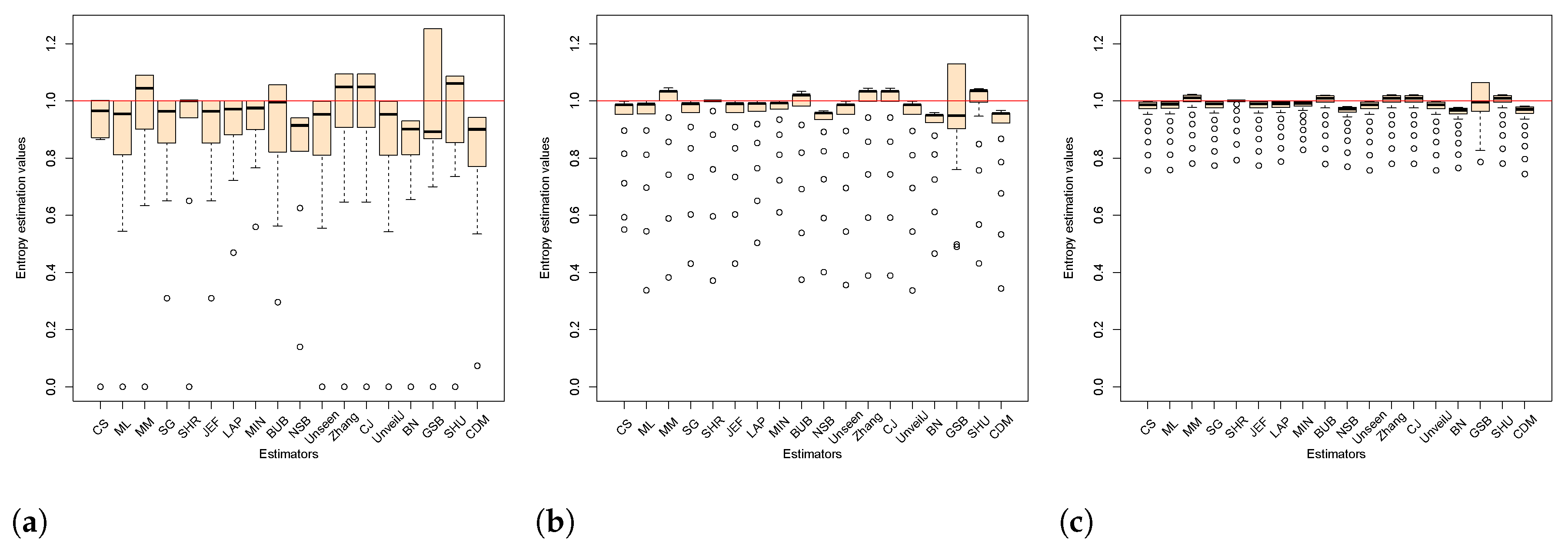
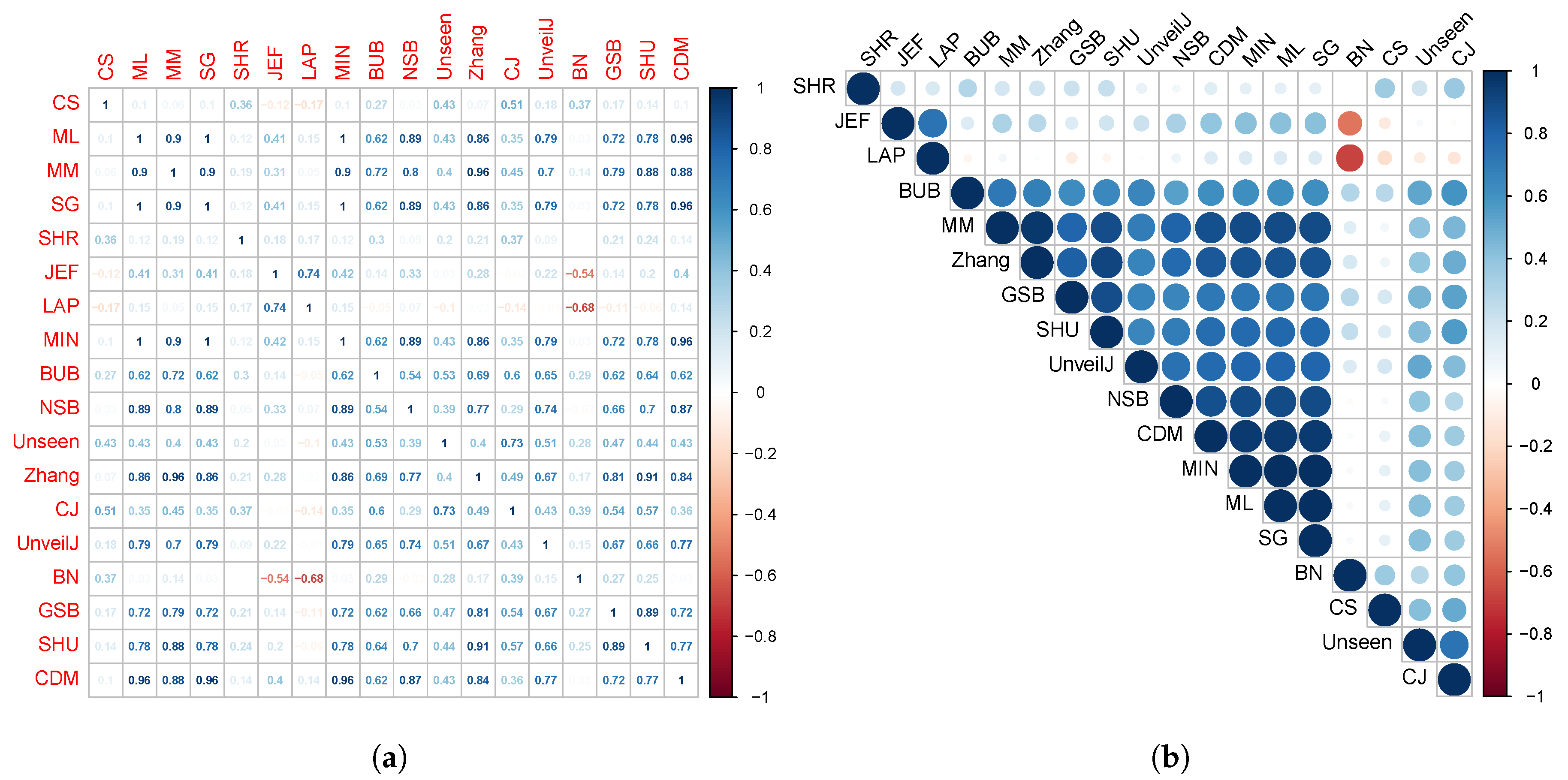
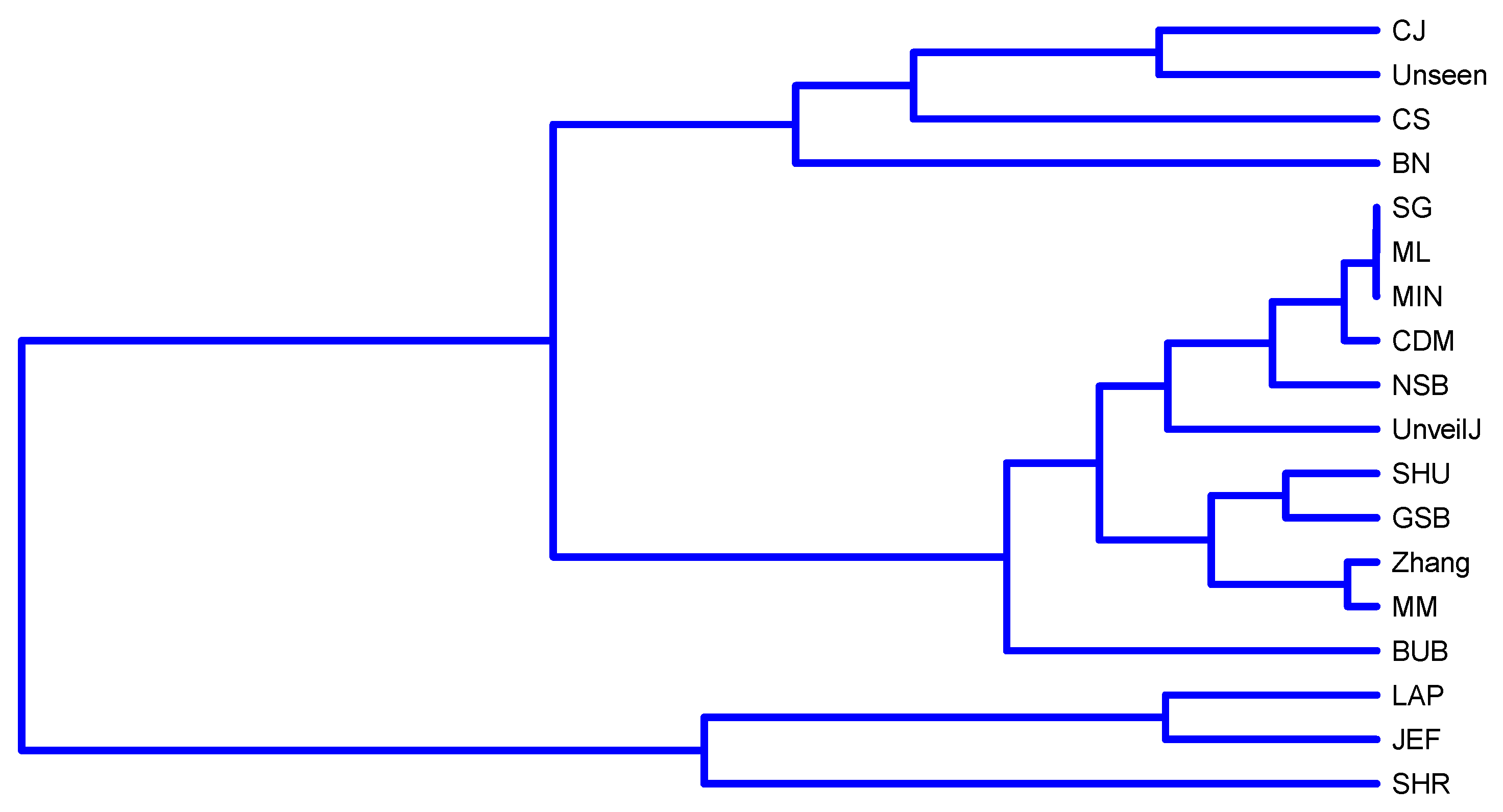
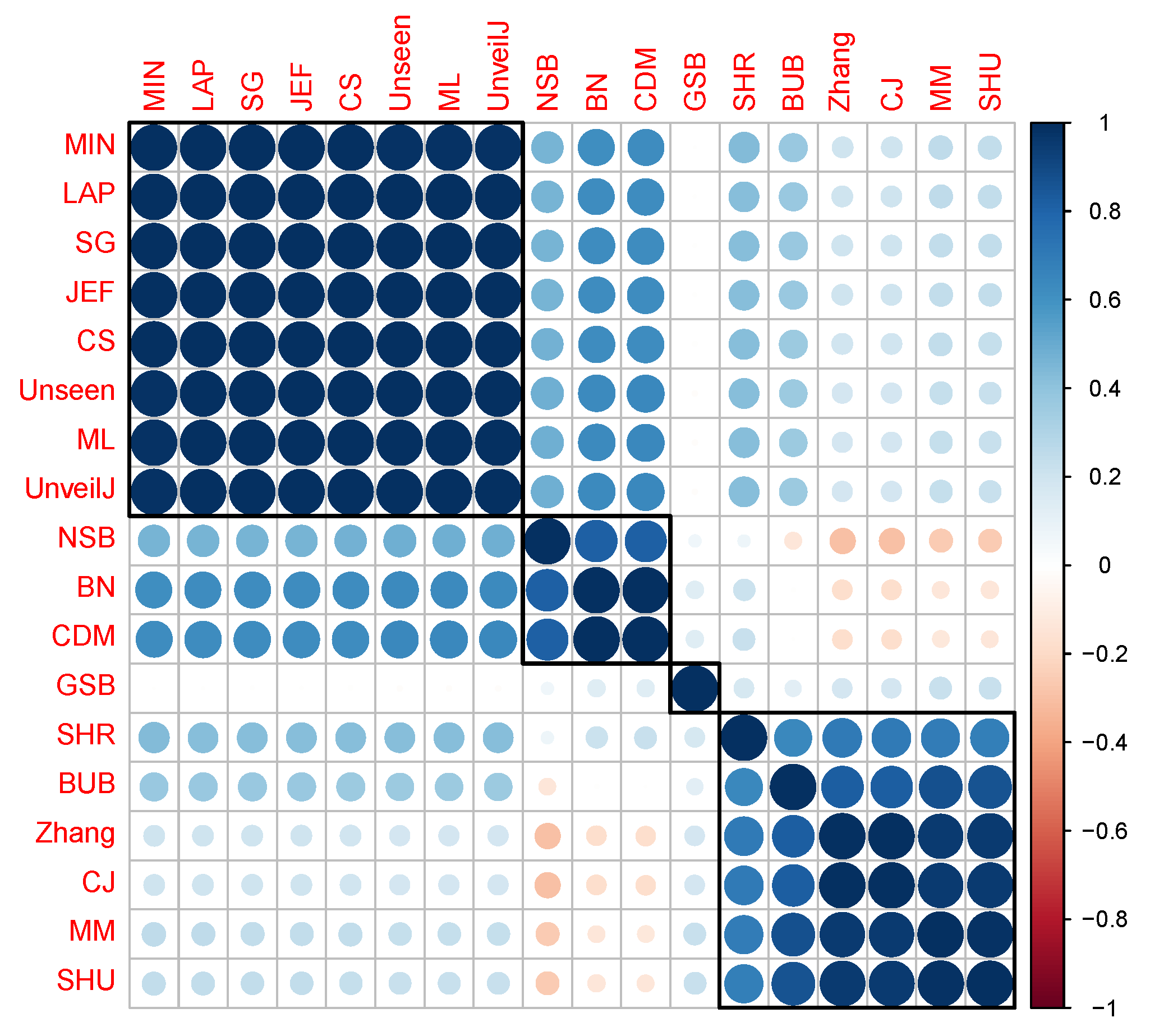
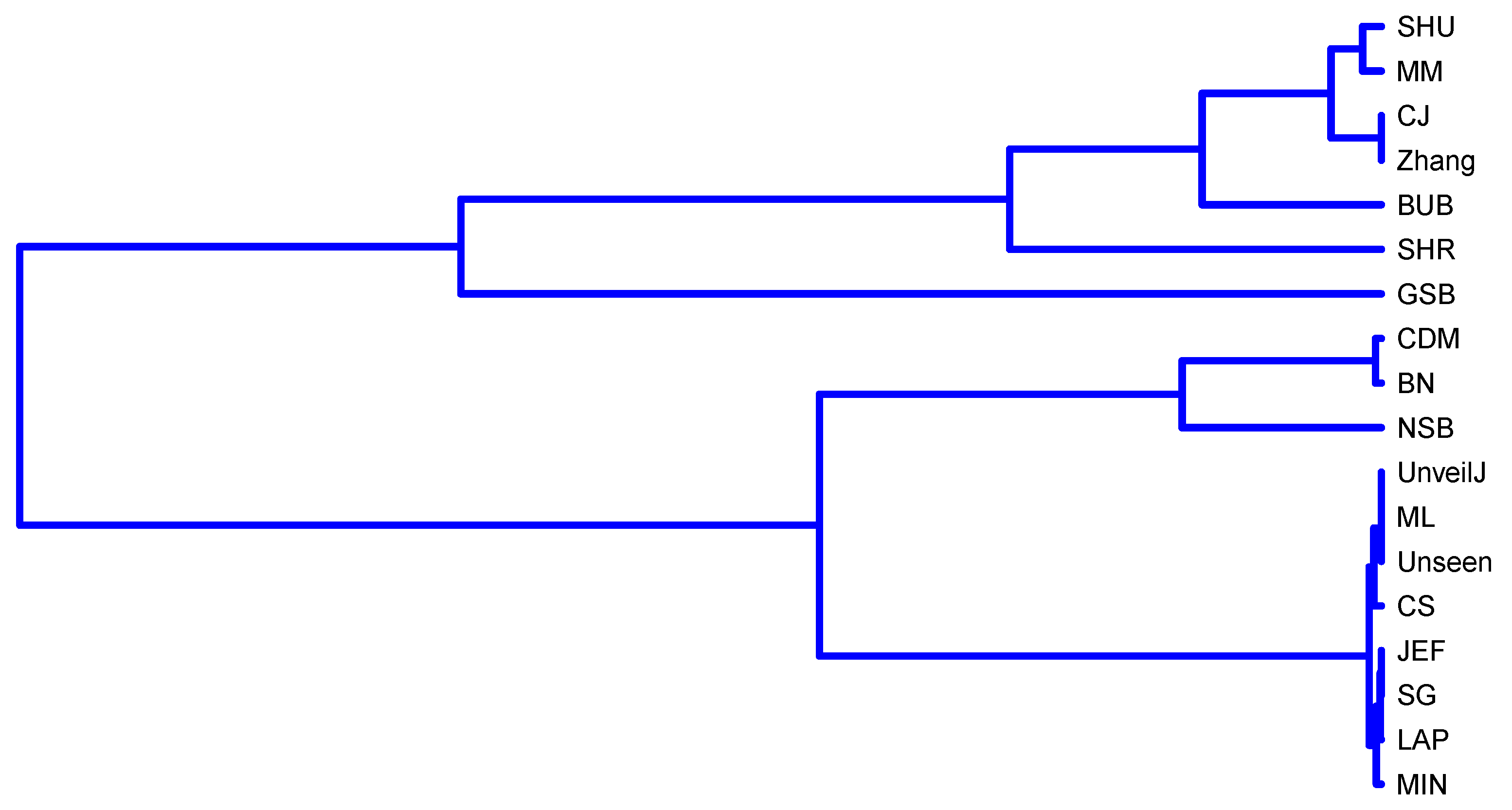
4.4. Correlation between Estimators of Entropy Using Bias
- { JEF, LAP, BN},
- { MM, BUB, ML, SG, MIN, Zhang, NSB, CDM, UnveilJ, GSB, SHU},
- { CS, Unseen, CJ}.
- { SHR}.
- { NSB, CDM, BN},
- { ML, SG, MIN, JEF, LAP, UnveilJ, CS, Unseen},
- { GSB}.
- { SHU, MM, CJ, Zhang, BUB, SHR}.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Verdú, S. Empil Estimation of Information Measures: A Literature guide. Entropy 2019, 21, 720. [Google Scholar] [CrossRef]
- Vu, V.Q.; Yu, B.; Kass, R.E. Coverage-adjusted entropy estimation. Stat. Med. 2007, 26, 4039–4060. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Archer, E.; Park, I.M.; Pillow, J.W. Bayesian entropy estimation for countable discrete distributions. J. Mach. Learn. Res. 2014, 15, 2833–2868. [Google Scholar]
- Timme, N.M.; Lapish, C. A tutorial for information theory in neuroscience. eNeuro 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Sechidis, K.; Azzimonti, L.; Pocock, A.; Corani, G.; Weatherall, J.; Brown, G. Efficient feature selection using shrinkage estimators. Mach. Learn. 2019, 108, 1261–1286. [Google Scholar] [CrossRef]
- Choudhury, P.; Kumar, K.R.; Nandi, S.; Athithan, G. An empirical approach towards characterization of encrypted and unencrypted VoIP traffic. Multimed. Tools Appl. 2020, 79, 603–631. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, H.; Knill, E. Efficient randomness certification by quantum probability estimation. Phys. Rev. Res. 2020, 2, 13016. [Google Scholar] [CrossRef]
- Meyer, P.E.; Lafitte, F.; Bontempi, G. Minet: A r/bioconductor package for inferring large transcriptional networks using mutual information. BMC Bioinform. 2008, 9, 1–10. [Google Scholar] [CrossRef]
- Kurt, Z.; Aydin, N.; Altay, G. Comprehensive review of association estimators for the inference of gene networks. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 695–718. [Google Scholar] [CrossRef]
- Schulman, J.S., Jr. Entropy: An Essential Component of Cryptographic Security. J. Cybersecur. Aware. Educ. 2019, 1, 29–38. [Google Scholar]
- Dai, S.; Guo, D. Comparing security notions of secret sharing schemes. Entropy 2015, 17, 1135–1145. [Google Scholar] [CrossRef]
- Austrin, P.; Chung, K.M.; Mahmoody, M.; Pass, R.; Seth, K. On the Impossibility of Cryptography with Tamperable Randomness. Algorithmica 2017, 79, 1052–1101. [Google Scholar] [CrossRef]
- Yasser, I.; Mohamed, M.A.; Samra, A.S.; Khalifa, F. A chaotic-based encryption/decryption framework for secure multimedia communications. Entropy 2020, 22, 1253. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, C.; Deng, X. An Efficient Image Encryption Scheme Based on the LSS Chaotic Map and Single S-Box. IEEE Access 2020, 8, 25664–25678. [Google Scholar] [CrossRef]
- Knuth, D. The Art of Computer Programming: Volume 2, Seminumerical Algoritms; Addison-Wesley Professional: Reading, MA, USA, 1981. [Google Scholar]
- Pseudorandom Number Sequence Test Program. 2011. Available online: http://www.fourmilab.ch/random/ (accessed on 18 April 2021).
- Marsaglia, George; The Marsaglia Random Number CDROM Including the Diehard Battery of Tests of Randomness; Natl. Sci. Found. (Grants DMS-8807976 DMS-9206972). 1995. Available online: http://stat.fsu.edu/pub/diehard/ (accessed on 18 April 2021).
- Rukhin, A.; Soto, J.; Nechvatal, J.; Miles, S.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. SP800-22: A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Booz-Allen and Hamilton Inc Mclean VA; 2010. Available online: http://csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22rev1a.pdf (accessed on 22 April 2021).
- L’ecuyer, P.; Simard, R. TestU01: A C library for empirical testing of random number generators. ACM Trans. Math. Softw. 2007, 33. [Google Scholar] [CrossRef]
- Madarro-Capó, E.J.; Legón-Pérez, C.M.; Rojas, O.; Sosa-Gómez, G.; Socorro-Llanes, R. Bit independence criterion extended to stream ciphers. Appl. Sci. 2020, 10, 7668. [Google Scholar] [CrossRef]
- Madarro Capó, E.J.; Cuellar, O.J.; Legón Pérez, C.M.; Gómez, G.S. Evaluation of input—Output statistical dependence PRNGs by SAC. In Proceedings of the 2016 International Conference on Software Process Improvement (CIMPS), Aguascalientes, Mexico, 12–14 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Miller, G. Note on the bias of information estimates. Inf. Theory Psychol. Probl. Methods 1955, 71, 108. [Google Scholar]
- Nemenman, I.; Shafee, F.; Bialek, W. Entropy and Inference, Revisited. arXiv 2001, arXiv:0108025. [Google Scholar]
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6, 414–427. [Google Scholar] [CrossRef] [PubMed]
- Chao, A.; Shen, T.J. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 2003, 10, 429–443. [Google Scholar] [CrossRef]
- Holste, D.; Große, I.; Herzel, H. Bayes’ estimators of generalized entropies. J. Phys. A. Math. Gen. 1998, 31, 2551–2566. [Google Scholar] [CrossRef]
- Krichevsky, R.E.; Trofimov, V.K. The Performance of Universal Encoding. IEEE Trans. Inf. Theory 1981, 27, 199–207. [Google Scholar] [CrossRef]
- Trybula, S. Some problems of simultaneous minimax estimation. Ann. Math. Stat. 1958, 29, 245–253. [Google Scholar] [CrossRef]
- Hausser, J.; Strimmer, K. Entropy inference and the james-stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Valiant, G.; Valiant, P. Estimating the unseen: Improved estimators for entropy and other properties. J. ACM 2017, 64, 1–41. [Google Scholar] [CrossRef]
- Zhang, Z. Entropy estimation in Turing’s perspective. Neural Comput. 2012, 24, 1368–1389. [Google Scholar] [CrossRef] [PubMed]
- Daub, C.O.; Steuer, R.; Selbig, J.; Kloska, S. Estimating mutual information using B-spline functions—An improved similarity measure for analysing gene expression data. BMC Bioinform. 2004, 5, 118. [Google Scholar] [CrossRef] [PubMed]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Van Huile, M.M. Edgeworth approximation of multivariate differential entropy. Neural Comput. 2005, 17, 1903–1910. [Google Scholar] [CrossRef] [PubMed]
- Vinck, M.; Battaglia, F.P.; Balakirsky, V.B.; Vinck, A.J.; Pennartz, C. Estimation of the entropy on the basis of its polynomial representation. IEEE Int. Symp. Inf. Theory Proc. 2012, 85, 1054–1058. [Google Scholar] [CrossRef]
- Kozachenko, L.F.; Leonenko, N.N. Sample Estimate of the Entropy of a Random Vector. Probl. Inf. Transm. 1987, 23, 95–101. [Google Scholar]
- Bonachela, J.A.; Hinrichsen, H.; Mũoz, M.A. Entropy estimates of small data sets. J. Phys. A Math. Theor. 2008, 41, 202001. [Google Scholar] [CrossRef]
- Grassberger, P. Entropy estimates from insufficient samplings. arXiv 2003, arXiv:0307138. [Google Scholar]
- Schürmann, T. Bias analysis in entropy estimation. J. Phys. A. Math. Gen. 2004, 37, L295. [Google Scholar] [CrossRef]
- Chao, A.; Wang, Y.T.; Jost, L. Entropy and the species accumulation curve: A novel entropy estimator via discovery rates of new species. Methods Ecol. Evol. 2013, 4, 1091–1100. [Google Scholar] [CrossRef]
- Burnham, K.P.; Overton, W.S. Estimation of the Size of a Closed Population when Capture Probabilities vary Among Animals. Biometrika 1978, 65, 625. [Google Scholar] [CrossRef]
- Archer, E.; Park, I.M.; Pillow, J.W. Bayesian entropy estimation for binary spike train data using parametric prior knowledge. Adv. Neural Inf. Process. Syst. 2013, 15, 1700–1708. [Google Scholar]
- Valiant, G.; Valiant, P. Estimating the unseen: An n/log(n)-sample estimator for entropy and support size, shown optimal via new CLTs. Proc. Annu. ACM Symp. Theory Comput. 2011, 685–694. [Google Scholar] [CrossRef]
- Nemenman, I. Coincidences and estimation of entropies of random variables with large cardinalities. Entropy 2011, 13, 2013–2023. [Google Scholar] [CrossRef]
- Al-Omari, A.I. New entropy estimators with smaller root mean squared error. J. Mod. Appl. Stat. Methods 2015, 14, 88–109. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841. [Google Scholar] [CrossRef] [PubMed]
- Schürmann, T. A note on entropy estimation. Neural Comput. 2015, 27, 2097–2106. [Google Scholar] [CrossRef]
- de Matos Simoes, R.; Emmert-Streib, F. Influence of Statistical Estimators on the Large-Scale Causal Inference of Regulatory Networks. Stat. Mach. Learn. Approaches Netw. Anal. 2012, 6, 131–152. [Google Scholar] [CrossRef]
- Müller, S. Linux Random Number Generator-A New Approach. 2018. Available online: http://www.chronox.de/lrng/doc/lrng.pdf (accessed on 22 April 2021).
- Marton, K.; Suciu, A.; Ignat, I. Randomness in digital cryptography: A survey. Rom. J. Inf. Sci. Technol. 2010, 13, 219–240. [Google Scholar]
- Zhang, Z.; Grabchak, M. Nonparametric estimation of Küllback-Leibler divergence. Neural Comput. 2014, 26, 2570–2593. [Google Scholar] [CrossRef]
- GitHub—Simomarsili/ndd: Bayesian Entropy Estimation in Python—Via the Nemenman-Schafee-Bialek Algorithm. Available online: https://github.com/simomarsili/ndd (accessed on 15 March 2021).
- Marcon, E.; Herault, B. entropart: An R package to measure and partition diversity. J. Stat. Softw. 2015, 11, 1–26. [Google Scholar]
- GitHub—Pillowlab/CDMentropy: Centered Dirichlet Mixture Entropy Estimator for Binary Data. Available online: https://github.com/pillowlab/CDMentropy (accessed on 15 March 2021).
- Rosenblad, A. The Concise Encyclopedia of Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 38, pp. 867–868. [Google Scholar] [CrossRef]
- Yim, O.; Ramdeen, K.T. Hierarchical Cluster Analysis: Comparison of Three Linkage Measures and Application to Psychological Data. Quant. Methods Psychol. 2015, 11, 8–21. [Google Scholar] [CrossRef]
- Ma, X.; Dhavala, S. Hierarchical clustering with prior knowledge. arXiv 2018, arXiv:1806.03432. [Google Scholar]



| Known as | Notation | Estimator | |
|---|---|---|---|
| Miller-Madow correction [25] | MM | , with m the number of such that | |
| Jackknife [44] | UnveilJ | , donde is the entropy of the sample original without the i-th symbol | |
| Best Upper Bound [4] | BUB | , where and | |
| Grassberger [41] | GSB | , where is the digamma function | |
| Schürmann [42] | SHU | ||
| Chao-Chen [28] | CS | , where | |
| James-Stein [32] | SHR | , where with and = | |
| Bonachela [40] | BN | ||
| Zhang [34] | Zhang | , where | |
| Chao-Wang-Jost [43] | CWJ | with where denote the number of singletons and denote the number of doubletons in the sample. | |
| Jeffrey [30] | JEF | , where with | |
| Laplace [29] | LAP | ||
| Schürmann- Grassberger [27] | SG | ||
| Minimax prior [31] | MIN | ||
| NSB [26] | NSB | , where , with , and is the expectation value of the m-th entropy moment at fixed ; exact expression for is given in [49]. | |
| CDM [45] | CDM | where | |
| Unseen [33] | Unseen | The authors propose to compute its value algorithmically. |
| Estimators | Sample Sizes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 | |
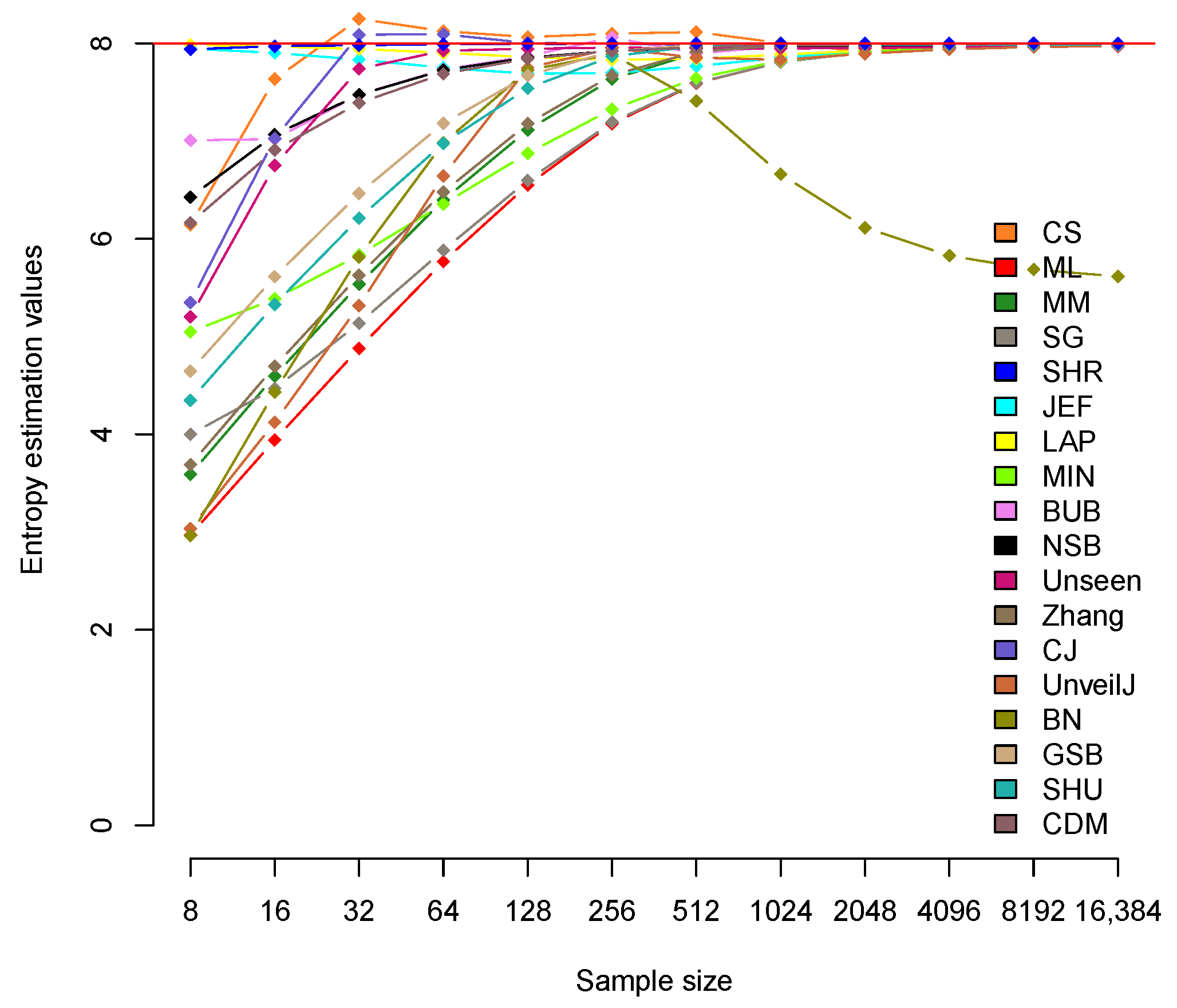
| CS | 6.142 | 7.635 | 8.251 | 8.126 | 8.064 | 8.099 | 8.116 | 8.003 | 7.914 | 7.940 | 7.963 | 7.974 |
| ML | 2.969 | 3.943 | 4.880 | 5.768 | 6.550 | 7.178 | 7.591 | 7.809 | 7.908 | 7.955 | 7.977 | 7.989 |
| MM | 3.590 | 4.598 | 5.536 | 6.397 | 7.113 | 7.633 | 7.902 | 7.985 | 7.998 | 7.999 | 8.000 | 8.000 |
| SG | 3.999 | 4.470 | 5.136 | 5.884 | 6.598 | 7.194 | 7.595 | 7.809 | 7.908 | 7.955 | 7.977 | 7.989 |
| SHR | 7.940 | 7.971 | 7.982 | 7.991 | 7.995 | 7.998 | 7.999 | 7.999 | 8.000 | 8.000 | 8.000 | 8.000 |
| JEF | 7.947 | 7.902 | 7.834 | 7.751 | 7.690 | 7.696 | 7.767 | 7.854 | 7.919 | 7.957 | 7.978 | 7.989 |
| LAP | 7.983 | 7.969 | 7.943 | 7.904 | 7.859 | 7.832 | 7.842 | 7.883 | 7.928 | 7.960 | 7.979 | 7.989 |
| MIN | 5.048 | 5.385 | 5.835 | 6.357 | 6.875 | 7.326 | 7.643 | 7.823 | 7.912 | 7.956 | 7.978 | 7.989 |
| BUB | 7.008 | 7.021 | 7.476 | 7.732 | 7.868 | 8.061 | 7.896 | 7.971 | 7.983 | 7.985 | 7.985 | 7.985 |
| NSB | 6.427 | 7.065 | 7.474 | 7.726 | 7.855 | 7.922 | 7.953 | 7.969 | 7.977 | 7.981 | 7.983 | 7.984 |
| Unseen | 5.202 | 6.751 | 7.739 | 7.925 | 7.945 | 7.957 | 7.950 | 7.948 | 7.953 | 7.960 | 7.966 | 7.971 |
| Zhang | 3.690 | 4.696 | 5.627 | 6.478 | 7.178 | 7.674 | 7.916 | 7.979 | 7.985 | 7.985 | 7.985 | 7.985 |
| CJ | 5.349 | 7.028 | 8.089 | 8.093 | 8.004 | 7.996 | 7.987 | 7.985 | 7.985 | 7.985 | 7.985 | 7.985 |
| UnveilJ | 3.036 | 4.124 | 5.316 | 6.645 | 7.749 | 7.95 | 7.855 | 7.832 | 7.894 | 7.940 | 7.963 | 7.974 |
| BN | 2.963 | 4.433 | 5.815 | 6.981 | 7.726 | 7.889 | 7.41 | 6.662 | 6.115 | 5.829 | 5.686 | 5.616 |
| GSB | 4.646 | 5.613 | 6.464 | 7.182 | 7.670 | 7.921 | 7.981 | 7.985 | 7.985 | 7.985 | 7.985 | 7.985 |
| SHU | 4.347 | 5.329 | 6.210 | 6.978 | 7.541 | 7.868 | 7.972 | 7.985 | 7.985 | 7.985 | 7.985 | 7.985 |
| CDM | 6.165 | 6.908 | 7.391 | 7.689 | 7.844 | 7.922 | 7.961 | 7.981 | 7.990 | 7.995 | 7.998 | 7.999 |
| Estimator | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 1.858 | 0.365 | −0.251 | −0.126 | −0.064 | −0.099 | −0.116 | −0.003 | 0.086 | 0.060 | 0.037 | 0.026 |
| ML | 5.031 | 4.057 | 3.120 | 2.232 | 1.450 | 0.822 | 0.409 | 0.191 | 0.092 | 0.045 | 0.023 | 0.011 |
| MM | 4.410 | 3.402 | 2.464 | 1.603 | 0.887 | 0.367 | 0.098 | 0.015 | 0.002 | 0.001 | 0.000 | 0.000 |
| SG | 4.001 | 3.530 | 2.864 | 2.116 | 1.402 | 0.806 | 0.405 | 0.191 | 0.092 | 0.045 | 0.023 | 0.011 |
| SHR | 0.060 | 0.029 | 0.018 | 0.009 | 0.005 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| JEF | 0.053 | 0.098 | 0.166 | 0.249 | 0.310 | 0.304 | 0.233 | 0.146 | 0.081 | 0.043 | 0.022 | 0.011 |
| LAP | 0.017 | 0.031 | 0.057 | 0.096 | 0.141 | 0.168 | 0.158 | 0.117 | 0.072 | 0.040 | 0.021 | 0.011 |
| MIN | 2.952 | 2.615 | 2.165 | 1.643 | 1.125 | 0.674 | 0.357 | 0.177 | 0.088 | 0.044 | 0.022 | 0.011 |
| BUB | 0.992 | 0.979 | 0.524 | 0.268 | 0.132 | -0.061 | 0.104 | 0.029 | 0.017 | 0.015 | 0.015 | 0.015 |
| NSB | 1.573 | 0.935 | 0.526 | 0.274 | 0.145 | 0.078 | 0.047 | 0.031 | 0.023 | 0.019 | 0.017 | 0.016 |
| Unseen | 2.798 | 1.249 | 0.261 | 0.075 | 0.055 | 0.043 | 0.050 | 0.052 | 0.047 | 0.040 | 0.034 | 0.029 |
| Zhang | 4.310 | 3.304 | 2.373 | 1.522 | 0.822 | 0.326 | 0.084 | 0.021 | 0.015 | 0.015 | 0.015 | 0.015 |
| CJ | 2.651 | 0.972 | −0.089 | −0.093 | −0.004 | 0.004 | 0.013 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 |
| UnveilJ | 4.964 | 3.876 | 2.684 | 1.355 | 0.251 | 0.050 | 0.145 | 0.168 | 0.106 | 0.060 | 0.037 | 0.026 |
| BN | 5.037 | 3.567 | 2.185 | 1.019 | 0.274 | 0.111 | 0.590 | 1.338 | 1.885 | 2.171 | 2.314 | 2.384 |
| GSB | 3.354 | 2.387 | 1.536 | 0.818 | 0.330 | 0.079 | 0.019 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 |
| SHU | 3.653 | 2.671 | 1.79 | 1.022 | 0.459 | 0.132 | 0.028 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 |
| CDM | 1.835 | 1.092 | 0.609 | 0.311 | 0.156 | 0.078 | 0.039 | 0.019 | 0.010 | 0.005 | 0.002 | 0.001 |
| Estimator | Sample Sizes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 | |
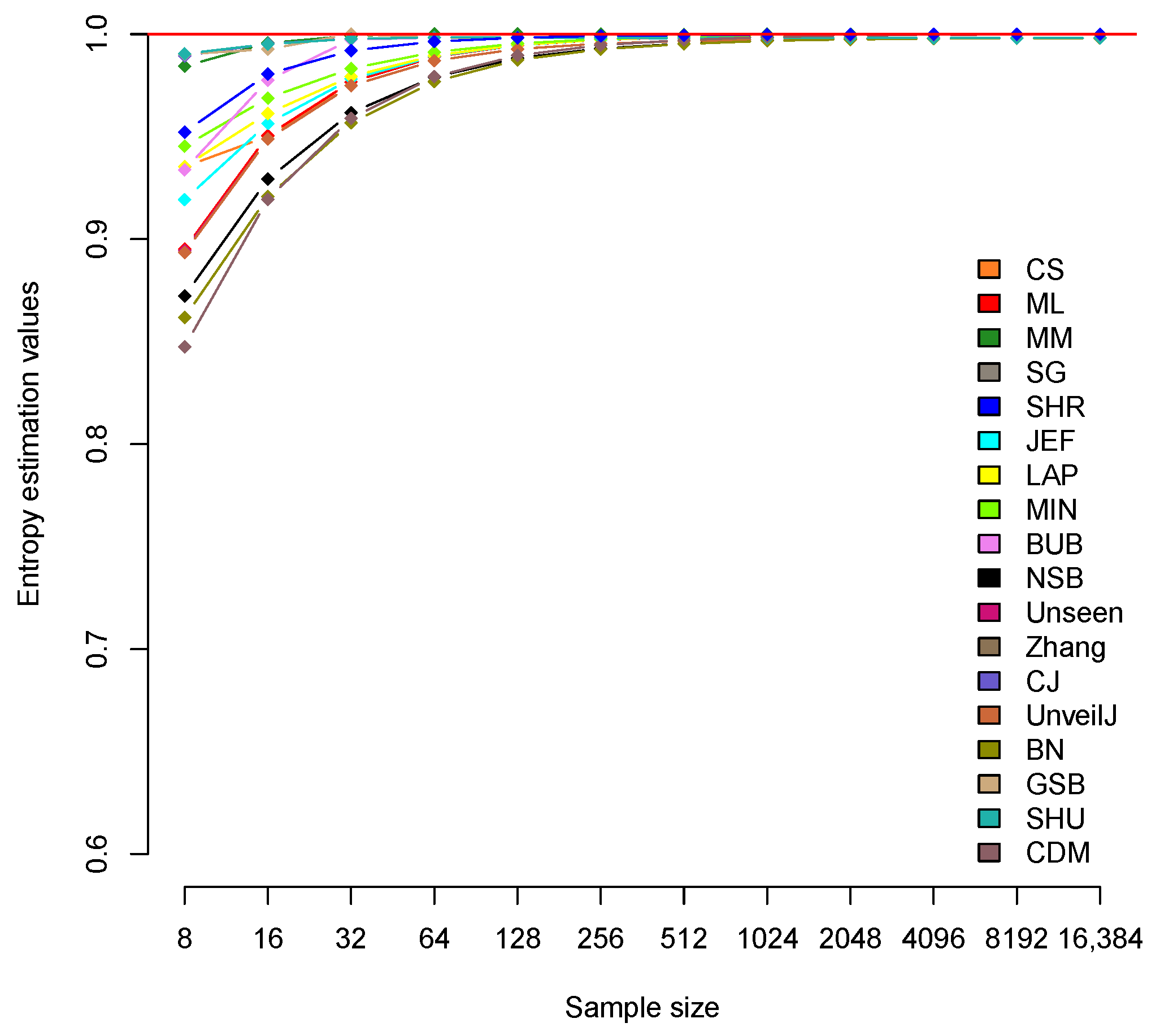
| CS | 0.935 | 0.95 | 0.975 | 0.987 | 0.993 | 0.995 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 | 0.998 |
| ML | 0.895 | 0.951 | 0.977 | 0.989 | 0.995 | 0.997 | 0.998 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| MM | 0.984 | 0.996 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| SG | 0.919 | 0.956 | 0.978 | 0.989 | 0.995 | 0.997 | 0.998 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| SHR | 0.952 | 0.981 | 0.992 | 0.996 | 0.998 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| JEF | 0.919 | 0.956 | 0.978 | 0.989 | 0.995 | 0.997 | 0.998 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| LAP | 0.935 | 0.961 | 0.979 | 0.99 | 0.995 | 0.997 | 0.998 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| MIN | 0.945 | 0.969 | 0.983 | 0.991 | 0.995 | 0.998 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| BUB | 0.934 | 0.978 | 0.997 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| NSB | 0.872 | 0.929 | 0.962 | 0.979 | 0.988 | 0.993 | 0.995 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 |
| Unseen | 0.894 | 0.949 | 0.975 | 0.987 | 0.993 | 0.995 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 | 0.998 |
| Zhang | 0.989 | 0.995 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| CJ | 0.989 | 0.995 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| UnveilJ | 0.893 | 0.949 | 0.975 | 0.987 | 0.993 | 0.995 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 | 0.998 |
| BN | 0.862 | 0.921 | 0.957 | 0.977 | 0.987 | 0.993 | 0.995 | 0.997 | 0.997 | 0.998 | 0.998 | 0.998 |
| GSB | 0.990 | 0.993 | 1.000 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| SHU | 0.990 | 0.995 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| CDM | 0.847 | 0.919 | 0.959 | 0.979 | 0.990 | 0.995 | 0.997 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 |
| Estimator | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 0.065 | 0.05 | 0.025 | 0.013 | 0.007 | 0.005 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 |
| ML | 0.105 | 0.049 | 0.023 | 0.011 | 0.005 | 0.003 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| MM | 0.016 | 0.004 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| SG | 0.081 | 0.044 | 0.022 | 0.011 | 0.005 | 0.003 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| SHR | 0.048 | 0.019 | 0.008 | 0.004 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| JEF | 0.081 | 0.044 | 0.022 | 0.011 | 0.005 | 0.003 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| LAP | 0.065 | 0.039 | 0.021 | 0.01 | 0.005 | 0.003 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| MIN | 0.055 | 0.031 | 0.017 | 0.009 | 0.005 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| BUB | 0.066 | 0.022 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| NSB | 0.128 | 0.071 | 0.038 | 0.021 | 0.012 | 0.007 | 0.005 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 |
| Unseen | 0.106 | 0.051 | 0.025 | 0.013 | 0.007 | 0.005 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 |
| Zhang | 0.011 | 0.005 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| CJ | 0.011 | 0.005 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| UnveilJ | 0.107 | 0.051 | 0.025 | 0.013 | 0.007 | 0.005 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 |
| BN | 0.138 | 0.079 | 0.043 | 0.023 | 0.013 | 0.007 | 0.005 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 |
| GSB | 0.01 | 0.007 | 0.000 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| SHU | 0.01 | 0.005 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| CDM | 0.153 | 0.081 | 0.041 | 0.021 | 0.01 | 0.005 | 0.003 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 |
| Estimator | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 3.722 | 0.716 | 1.024 | 0.312 | 0.054 | 0.022 | 0.017 | 0.001 | 0.007 | 0.004 | 0.001 | 0.001 |
| ML | 25.315 | 16.469 | 9.744 | 4.989 | 2.106 | 0.678 | 0.168 | 0.037 | 0.009 | 0.002 | 0.001 | 0.000 |
| MM | 19.466 | 11.583 | 6.085 | 2.581 | 0.793 | 0.139 | 0.011 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| SG | 16.012 | 12.465 | 8.208 | 4.483 | 1.971 | 0.653 | 0.165 | 0.037 | 0.009 | 0.002 | 0.001 | 0.000 |
| SHR | 0.041 | 0.005 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| JEF | 0.003 | 0.01 | 0.028 | 0.062 | 0.097 | 0.093 | 0.055 | 0.021 | 0.007 | 0.002 | 0.000 | 0.000 |
| LAP | 0.000 | 0.001 | 0.003 | 0.009 | 0.02 | 0.028 | 0.025 | 0.014 | 0.005 | 0.002 | 0.000 | 0.000 |
| MIN | 8.719 | 6.841 | 4.693 | 2.704 | 1.268 | 0.456 | 0.129 | 0.032 | 0.008 | 0.002 | 0.000 | 0.000 |
| BUB | 1.100 | 1.043 | 0.39 | 0.125 | 0.036 | 0.013 | 0.012 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| NSB | 2.622 | 0.944 | 0.315 | 0.087 | 0.025 | 0.007 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 |
| Unseen | 8.000 | 1.859 | 0.71 | 0.328 | 0.079 | 0.018 | 0.006 | 0.004 | 0.003 | 0.002 | 0.001 | 0.001 |
| Zhang | 18.595 | 10.93 | 5.645 | 2.329 | 0.684 | 0.111 | 0.009 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| CJ | 7.134 | 1.129 | 0.68 | 0.349 | 0.061 | 0.012 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| UnveilJ | 24.658 | 15.051 | 7.246 | 1.929 | 0.092 | 0.023 | 0.024 | 0.028 | 0.011 | 0.004 | 0.001 | 0.001 |
| BN | 25.391 | 12.744 | 4.811 | 1.08 | 0.11 | 0.033 | 0.354 | 1.789 | 3.554 | 4.715 | 5.353 | 5.685 |
| GSB | 11.309 | 5.745 | 2.406 | 0.706 | 0.131 | 0.015 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| SHU | 13.386 | 7.164 | 3.233 | 1.07 | 0.227 | 0.025 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| CDM | 3.498 | 1.255 | 0.404 | 0.108 | 0.027 | 0.007 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Estimator | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 0.016 | 0.007 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ML | 0.033 | 0.008 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MM | 0.024 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| SG | 0.019 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| SHR | 0.019 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| JEF | 0.019 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| LAP | 0.012 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| MIN | 0.008 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BUB | 0.026 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| NSB | 0.028 | 0.008 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Unseen | 0.033 | 0.008 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Zhang | 0.024 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CJ | 0.024 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| UnveilJ | 0.034 | 0.008 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BN | 0.032 | 0.009 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| GSB | 0.063 | 0.015 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| SHU | 0.024 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CDM | 0.041 | 0.011 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras Rodríguez, L.; Madarro-Capó , E.J.; Legón-Pérez , C.M.; Rojas, O.; Sosa-Gómez, G. Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy. Entropy 2021, 23, 561. https://doi.org/10.3390/e23050561
Contreras Rodríguez L, Madarro-Capó EJ, Legón-Pérez CM, Rojas O, Sosa-Gómez G. Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy. Entropy. 2021; 23(5):561. https://doi.org/10.3390/e23050561
Chicago/Turabian StyleContreras Rodríguez, Lianet, Evaristo José Madarro-Capó , Carlos Miguel Legón-Pérez , Omar Rojas, and Guillermo Sosa-Gómez. 2021. "Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy" Entropy 23, no. 5: 561. https://doi.org/10.3390/e23050561
APA StyleContreras Rodríguez, L., Madarro-Capó , E. J., Legón-Pérez , C. M., Rojas, O., & Sosa-Gómez, G. (2021). Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy. Entropy, 23(5), 561. https://doi.org/10.3390/e23050561








