Information Theory Based Evaluation of the RC4 Stream Cipher Outputs
Abstract
:1. Introduction
2. Preliminaries
2.1. Description of the RC4 Stream Encryption Algorithm
| Algorithm 1 RC4 key-scheduling. |
|
| Algorithm 2 RC4 pseudo-random generator. |
|
2.2. Iterative Probabilistic Attacks
2.3. Entropy As a Measure of Uncertainty
3. Definition of the Proposed Test Statistic
3.1. Basis of the Evaluation Criterion
3.2. Definition of the Test Statistic
3.3. Decision Criteria Using the Q-Statistic
4. Pre-Computing of Probabilities and Estimation of Entropies
4.1. Frequency Pre-Calculation
4.2. Estimation of Joint, Marginal, and Conditional Probabilities
4.3. Entropy Estimation
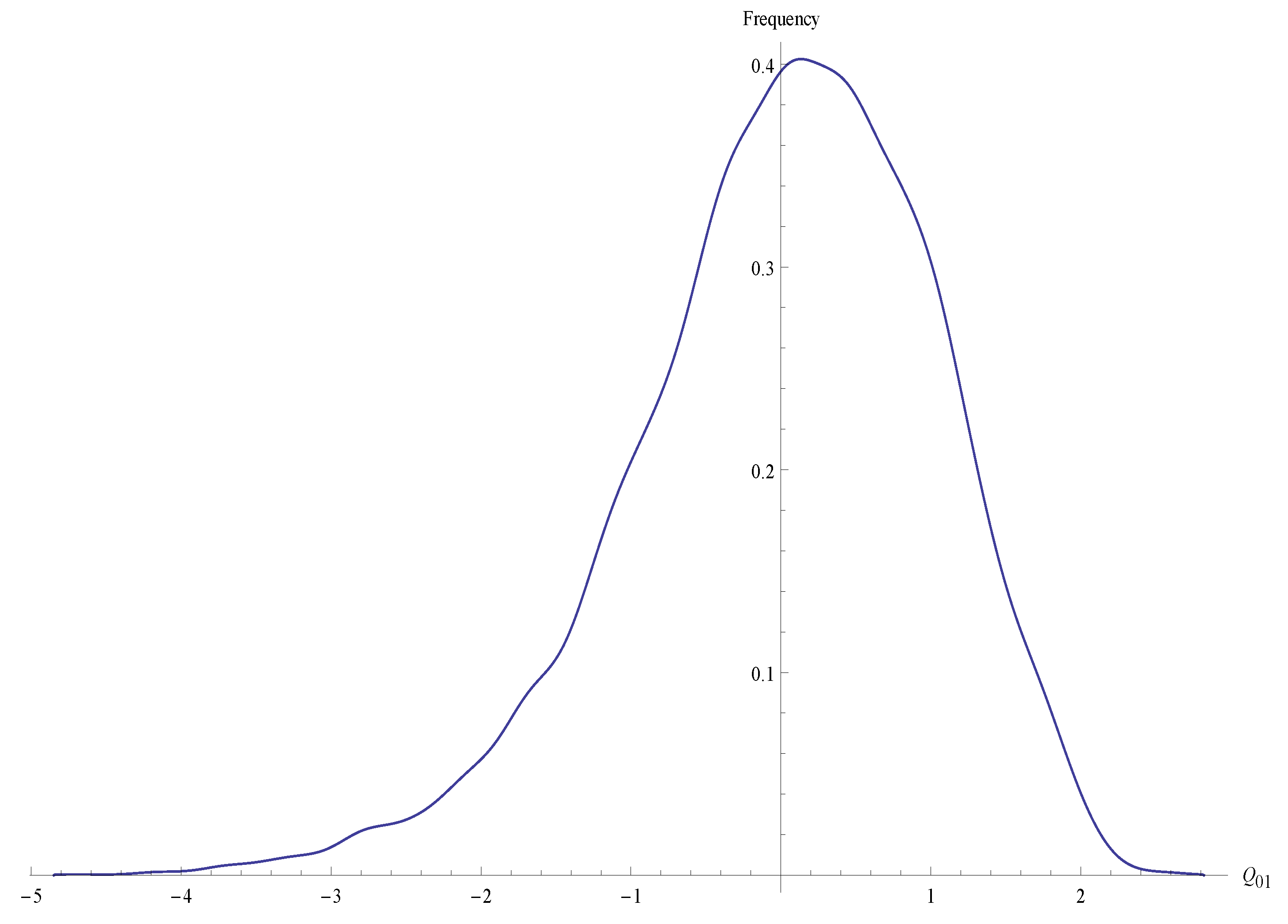
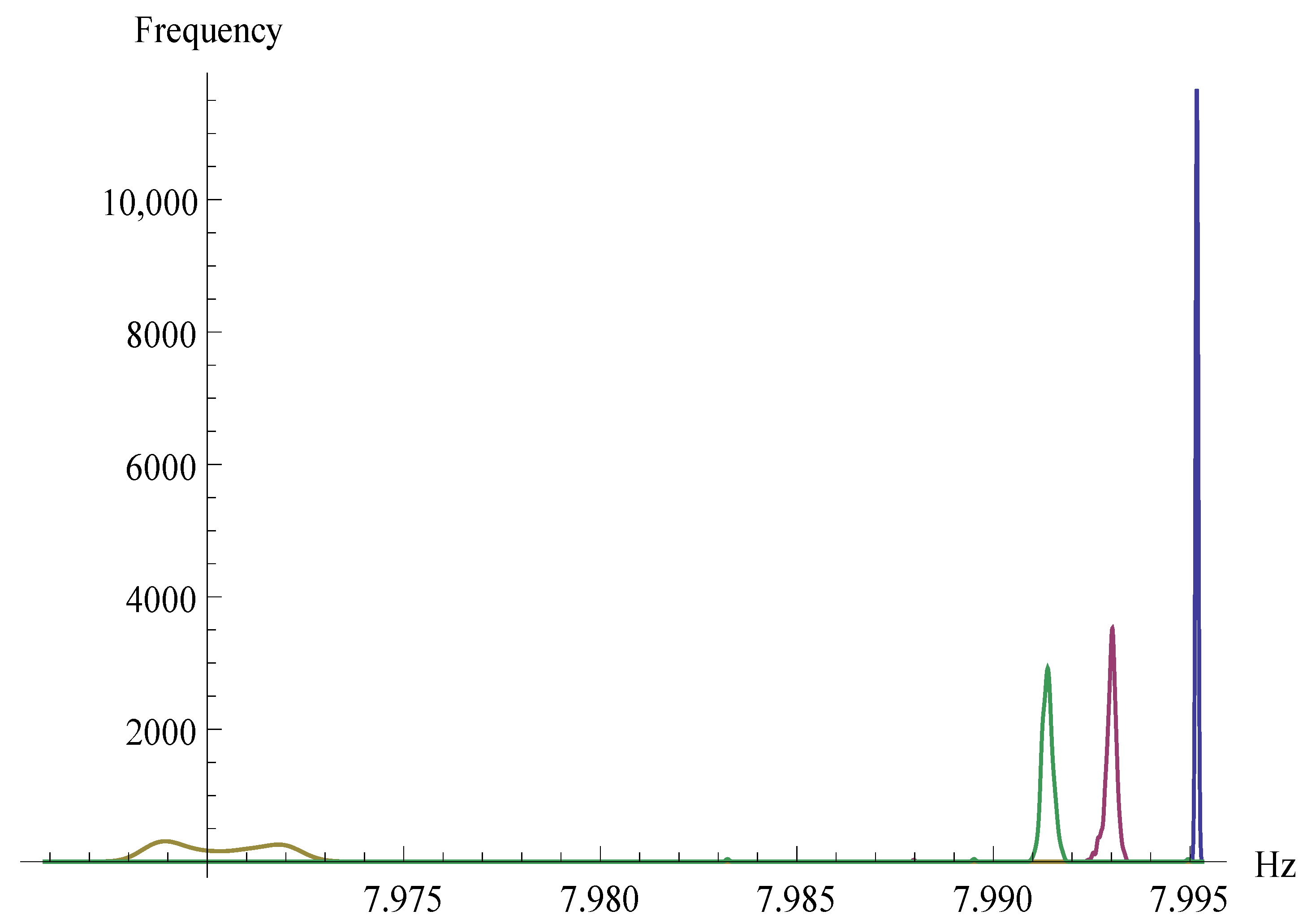
5. Experimental Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Knudsen, L.R.; Meier, W.; Preneel, B.; Rijmen, V.; Verdoolaege, S. Analysis methods for (Alleged) RC4. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1514, pp. 327–341. [Google Scholar] [CrossRef] [Green Version]
- Golić, J.D. Iterative probabilistic cryptanalysis of RC4 keystream generator. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1841, pp. 220–233. [Google Scholar] [CrossRef]
- Golic, J.D.; Morgari, G. Iterative Probabilistic Reconstruction of RC4 Internal States. IACR Cryptol. ePrint Arch. 2008, 2008, 348. [Google Scholar]
- Paul, G.; Maitra, S. RC4: Stream Cipher and Its Variants; CRC Press: Boca Raton, FL, USA, 2011; pp. 1–281. [Google Scholar] [CrossRef]
- RC4 Cipher Is No Longer Supported in Internet Explorer 11 or Microsoft Edge. Available online: https://support.microsoft.com/en-us/help/3151631/rc4-cipher-is-no-longer-supported-in-internet-explorer-11-or-microsoft (accessed on 18 July 2020).
- SSL Configuration Required to Secure Oracle HTTP Server After Applying Security Patch Updates. Available online: https://support.oracle.com/knowledge/Middleware/2314658{_}1.html (accessed on 18 July 2020).
- Satapathy, A.; Livingston, J. A Comprehensive Survey on SSL/ TLS and their Vulnerabilities. Int. J. Comput. Appl. 2016, 153, 31–38. [Google Scholar] [CrossRef]
- Soundararajan, E.; Kumar, N.; Sivasankar, V.; Rajeswari, S. Performance analysis of security algorithms. In Advances in Communication Systems and Networks; Springer: Singapore, 2020; Volume 656, pp. 465–476. [Google Scholar] [CrossRef]
- Jindal, P.; Makkar, S. Modified RC4 variants and their performance analysis. In Microelectronics, Electromagnetics and tElecommunications; Springer: Singapore, 2019; Volume 521, pp. 367–374. [Google Scholar] [CrossRef]
- Parah, S.A.; Sheikh, J.A.; Akhoon, J.A.; Loan, N.A.; Bhat, G.M. Information hiding in edges: A high capacity information hiding technique using hybrid edge detection. Multimed. Tools Appl. 2018, 77, 185–207. [Google Scholar] [CrossRef]
- Capó, E.J.M.; Cuellar, O.J.; Pérez, C.M.L.; Gómez, G.S. Evaluation of input—Output statistical dependence PRNGs by SAC. In Proceedings of the 2016 International Conference on Software Process Improvement (CIMPS), Aguascalientes, Mexico, 12–14 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Grosul, A.L.; Wallach, D.S. A Related-Key Cryptanalysis of RC4; Technical Report; Department of Computer Science, Rice University: Houston, TX, USA, 2000. [Google Scholar]
- Matsui, M. Key collisions of the RC4 stream cipher. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5665, pp. 38–50. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Miyaji, A. How to find short RC4 colliding key pairs. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7001, pp. 32–46. [Google Scholar] [CrossRef]
- Tyagi, M.; Manoria, M.; Mishra, B. Effective data storage security with efficient computing in cloud. Commun. Comput. Inf. Sci. 2019, 839, 153–164. [Google Scholar] [CrossRef]
- Dhiman, A.; Gupta, V.; Singh, D. Secure portable storage drive: Secure information storage. Commun. Comput. Inf. Sci. 2019, 839, 308–316. [Google Scholar] [CrossRef]
- Nita, S.L.; Mihailescu, M.I.; Pau, V.C. Security and cryptographic challenges for authentication based on biometrics data. Cryptography 2018, 2, 39. [Google Scholar] [CrossRef] [Green Version]
- Zelenoritskaya, A.V.; Ivanov, M.A.; Salikov, E.A. Possible Modifications of RC4 Stream Cipher. Mech. Mach. Sci. 2020, 80, 335–341. [Google Scholar] [CrossRef]
- Jindal, P.; Singh, B. Optimization of the Security-Performance Tradeoff in RC4 Encryption Algorithm. Wirel. Pers. Commun. 2017, 92, 1221–1250. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Pudovkina, M. The Number of Initial States of the RC4 Cipher with the Same Cycle Structure; Technical Report Mod L; Moscow Engineering Physics Institute (State University): Moscow, Russia, 2003. [Google Scholar]
- Mironov, I. (Not so) random shuffles of RC4. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2442, pp. 304–319. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhang, X. A normal law for the plug-in estimator of entropy. IEEE Trans. Inf. Theory 2012, 58, 2745–2747. [Google Scholar] [CrossRef]
- Miller, G. Note on the bias of information estimates. In Information Theory in Psychology: Problems and Methods; Free Press: Glencoe, IL, USA, 1955; pp. 95–100. [Google Scholar]
- Basharin, G.P. On a statistical estimate for the entropy of a sequence of independent random variables. Theory Probab. Appl. 1959, 4, 333–336. [Google Scholar] [CrossRef]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef] [Green Version]
- Van Den Broek, F.; Poll, E. A comparison of time-memory trade-off attacks on stream ciphers. In International Conference on Cryptology in Africa; Springer: Berlin/Heidelberg, Germany, 2013; pp. 406–423. [Google Scholar]
- Verdú, S. Empirical Estimation of Information Measures: A Literature Guide. Entropy 2019, 21, 720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| J/Z | 0 | 1 | … | 255 | |
|---|---|---|---|---|---|
| 0 | f(0,0) | f(0,1) | … | f(0,255) | |
| 1 | f(1,0) | f(1,1) | … | f(1,255) | |
| ⋮ | ⋮ | ⋮ | … | ⋮ | ⋮ |
| 255 | f(255,0) | f(255,1) | … | f(255,255) | |
| … | M |
| J/Z | 0 | … | … | 255 | |
|---|---|---|---|---|---|
| 0 | ⋮ | ||||
| ⋮ | ⋮ | ⋮ | |||
| ⋮ | ⋮ | ⋮ | … | ⋮ | |
| 255 |
| Z/T | 1 | 2 | … | 512 |
|---|---|---|---|---|
| 0 | … | |||
| 1 | … | |||
| ⋮ | ⋮ | ⋮ | … | ⋮ |
| 255 | … |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madarro-Capó , E.J.; Legón-Pérez , C.M.; Rojas, O.; Sosa-Gómez, G. Information Theory Based Evaluation of the RC4 Stream Cipher Outputs. Entropy 2021, 23, 896. https://doi.org/10.3390/e23070896
Madarro-Capó EJ, Legón-Pérez CM, Rojas O, Sosa-Gómez G. Information Theory Based Evaluation of the RC4 Stream Cipher Outputs. Entropy. 2021; 23(7):896. https://doi.org/10.3390/e23070896
Chicago/Turabian StyleMadarro-Capó , Evaristo José, Carlos Miguel Legón-Pérez , Omar Rojas, and Guillermo Sosa-Gómez. 2021. "Information Theory Based Evaluation of the RC4 Stream Cipher Outputs" Entropy 23, no. 7: 896. https://doi.org/10.3390/e23070896
APA StyleMadarro-Capó , E. J., Legón-Pérez , C. M., Rojas, O., & Sosa-Gómez, G. (2021). Information Theory Based Evaluation of the RC4 Stream Cipher Outputs. Entropy, 23(7), 896. https://doi.org/10.3390/e23070896








