A New Two-Stage Algorithm for Solving Optimization Problems
Abstract
1. Introduction
2. Literature Review
3. The New Two-Stage Optimization Algorithm
3.1. Theory of the TSO Algorithm
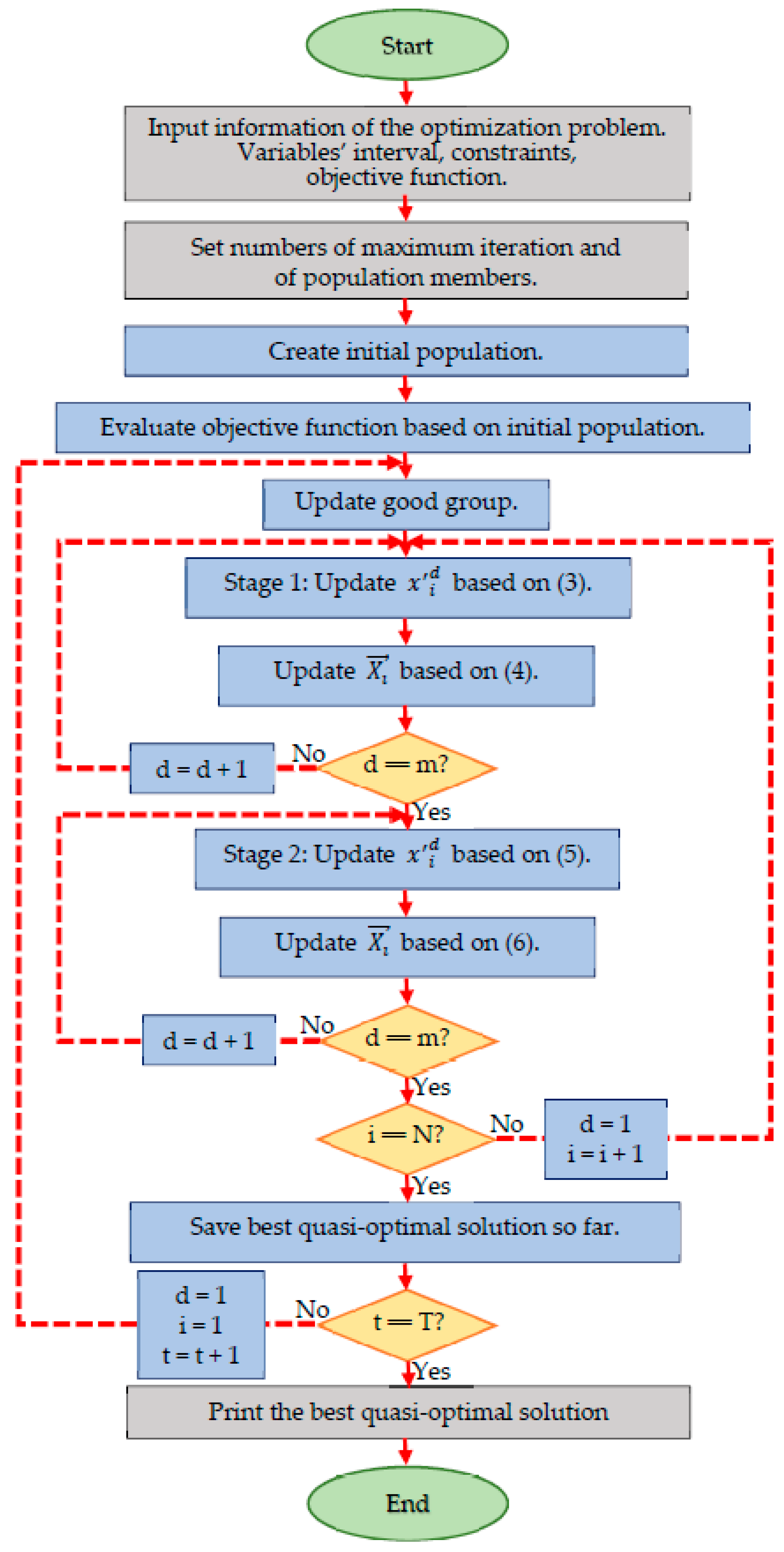
3.2. Mathematical Modeling of the TSO Algorithm
| Algorithm 1 Pseudo-code of the TSO approach. | ||
| Start the TSO algorithm. | ||
| 1. | Determine the range of decision variables, constraints and objective function of the problem. | |
| 2. | Create the initial population at random. | |
| 3. | Evaluate the objective function based on the initial population. | |
| 4. | For t = 1:T, with t being iteration number and T the maximum iteration: | |
| 5. | Update the good group. | |
| 6. | For i = 1:N, with N being the number of population members; | |
| 7. | For d = 1:m, with d being the contour and m the number of variables: | |
| 8. | Select the j’-th good member. | |
| 9. | Stage 1: Update based on (1). | |
| 10. | End for d = 1:m. | |
| 11. | Update based on (2). | |
| 12. | For d = 1:m: | |
| 13. | Select the k’-th good member, with k ≠ j. | |
| 14. | Stage 2: Update based on (3). | |
| 15. | End for d = 1:m. | |
| 16. | Update based on (4). | |
| 17. | End for i = 1:N. | |
| 18. | Save the best quasi-optimal solution. | |
| 19. | End for t = 1:T. | |
| 20. | Print the best quasi-optimal solution obtained by the TSO algorithm. | |
| End the TSO algorithm. | ||
4. Simulation Study and Results
4.1. Experimental Setup
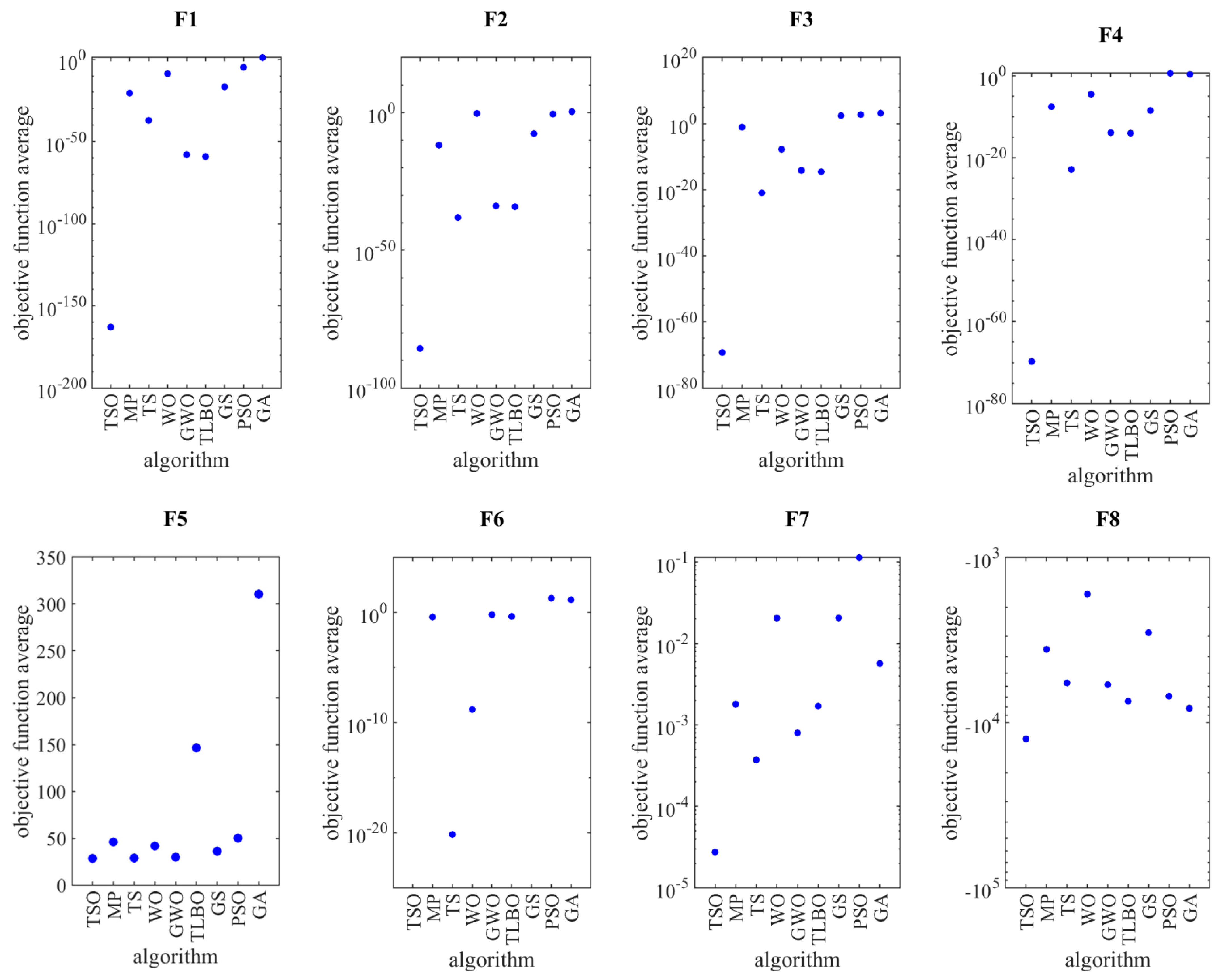
4.2. Evaluation for Unimodal Objective Functions
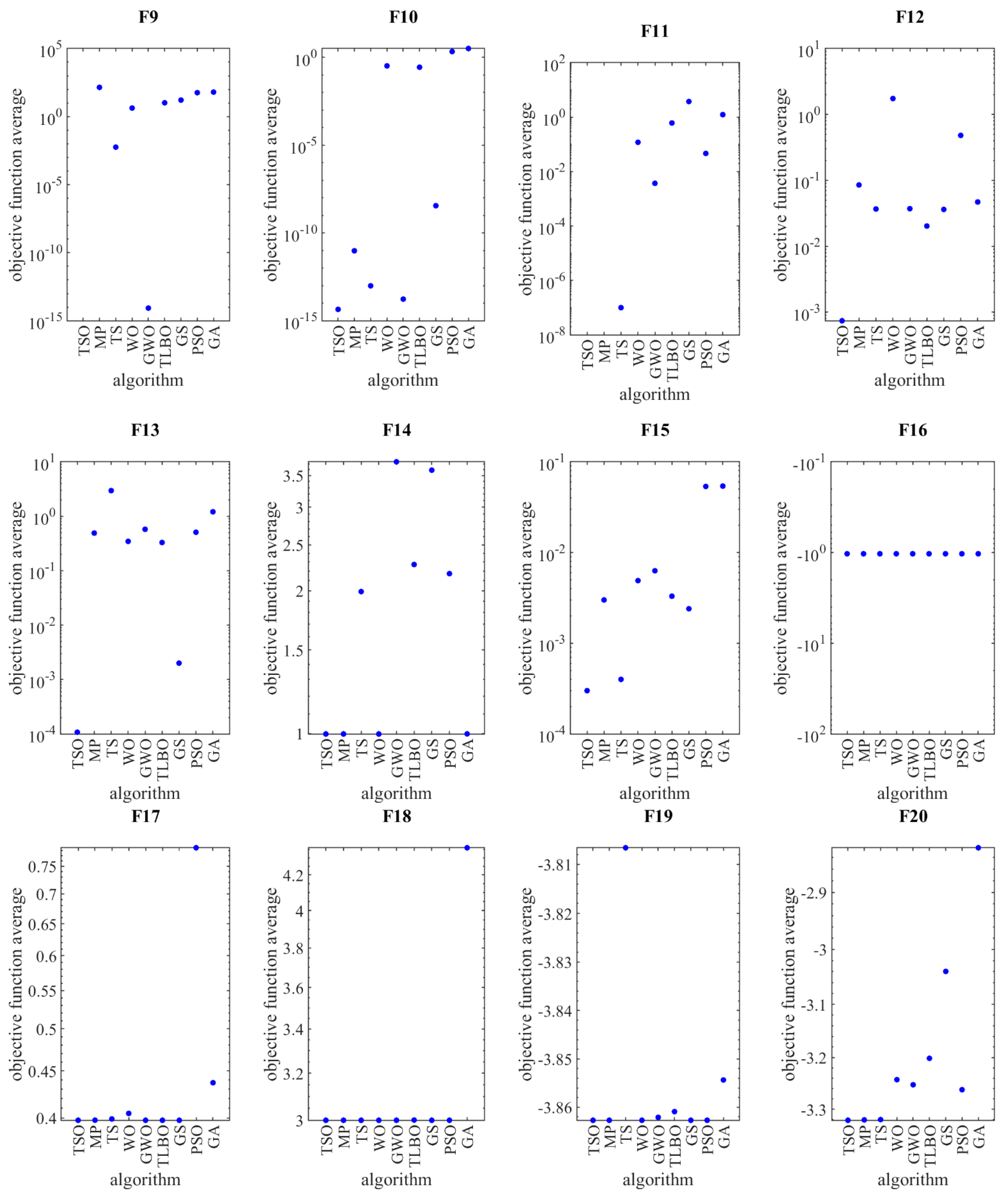
4.3. Evaluation for High-Dimesional Multimodal Objective Functions
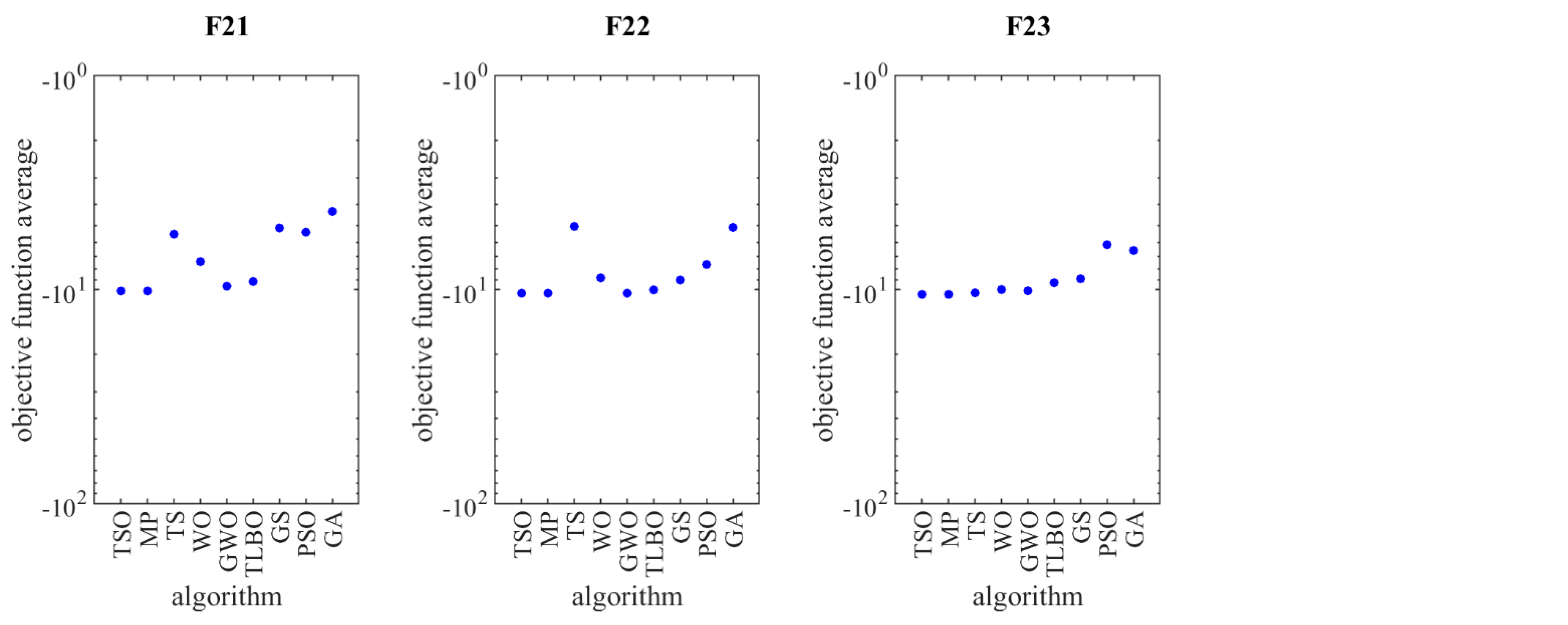
4.4. Evaluation for Fixed-Dimesional Multimodal Objective Functions
4.5. Statistical Testing
5. Discussion
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Objective Function | Variables’ Interval |
|---|---|
| Objective Function | Variables’ Interval |
|---|---|
where | |
| Objective Function | Variables’ Interval |
|---|---|
| [−5, 10][0, 15] | |
References
- Zelinka, I.; Snasael, V.; Abraham, A. Handbook of Optimization: From Classical to Modern Approach; Springer: New York, NY, USA, 2012. [Google Scholar]
- Beck, A.; Stoica, P.; Li, J. Exact and approximate solutions of source localization problems. IEEE Trans. Signal Process. 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M.H. A review of population-based meta-heuristic algorithms. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35. [Google Scholar]
- Palacios, C.A.; Reyes-Suarez, J.A.; Bearzotti, L.A.; Leiva, V.; Marchant, C. Knowledge discovery for higher education student retention based on data mining: Machine learning algorithms and case study in Chile. Entropy 2021, 23, 485. [Google Scholar] [CrossRef]
- Kawamoto, K.; Hirota, K. Random scanning algorithm for tracking curves in binary image sequences. Int. J. Intell. Comput. Med. Sci. Image Process. 2008, 2, 101–110. [Google Scholar] [CrossRef]
- Dhiman, G. SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowl.-Based Syst. 2021, 222, 106926. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Malik, O.P.; Guerrero, J.M.; Sotelo, C.; Sotelo, D.; Nazari-Heris, M.; Al-Haddad, K.; Ramirez-Mendoza, R.A. Genetic algorithm for energy commitment in a power system supplied by multiple energy carriers. Sustainability 2020, 12, 10053. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Hofmeyr, S.A.; Forrest, S. Architecture for an artificial immune system. Evol. Comput. 2000, 8, 443–473. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.R.; Abd Elaziz, M.; Xiong, S. Ludo game-based metaheuristics for global and engineering optimization. Appl. Soft Comput. 2019, 84, 105723. [Google Scholar] [CrossRef]
- Ji, Z.; Xiao, W. Improving decision-making efficiency of image game based on deep Q-learning. Soft Comput. 2020, 24, 8313–8322. [Google Scholar] [CrossRef]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Ramirez-Figueroa, J.A.; Martin-Barreiro, C.; Nieto, A.B.; Leiva, V.; Galindo, M.P. A new principal component analysis by particle swarm optimization with an environmental application for data science. Stoch. Environ. Res. Risk Assess. 2021. [Google Scholar] [CrossRef]
- Cheng, Z.; Song, H.; Wang, J.; Zhang, H.; Chang, T.; Zhang, M. Hybrid firefly algorithm with grouping attraction for constrained optimization problem. Knowl. Based Syst. 2021, 220, 106937. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Montazeri, Z.; Niknam, T. Optimal utilization of electrical energy from power plants based on final energy consumption using gravitational search algorithm. Electr. Eng. Electromech. 2018, 4, 70–73. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Malik, O.P.; Morales-Menendez, R.; Dhiman, G.; Nouri, N.; Ehsanifar, A.; Guerrero, J.M.; Ramirez-Mendoza, R.A. Binary spring search algorithm for solving various optimization problems. Appl. Sci. 2021, 11, 1286. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Daniel, W.W. Applied Nonparametric Statistics; PWS-Kent Publisher: Boston, MA, USA, 1990. [Google Scholar]
- Korosec, P.; Eftimov, T. Insights into exploration and exploitation power of optimization algorithm using DSCTool. Mathematics 2020, 8, 1474. [Google Scholar] [CrossRef]
- Givi, H.; Dehghani, M.; Montazeri, Z.; Morales-Menendez, R.; Ramirez-Mendoza, R.A.; Nouri, N. GBUO: “The good, the bad, and the ugly” optimizer. Appl. Sci. 2021, 11, 2042. [Google Scholar] [CrossRef]
- Kang, H.; Bei, F.; Shen, Y.; Sun, X.; Chen, Q. A diversity model based on dimension entropy and its application to swarm intelligence algorithm. Entropy 2021, 23, 397. [Google Scholar] [CrossRef] [PubMed]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
| Genetic | PSO | GS | TLBO | GWO | WO | TS | MP | TSO | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | AV | 13.2405 | 1.7740 × 10−5 | 2.0255 × 10−17 | 8.3373 × 10−60 | 1.09 × 10−58 | 2.1741 × 10−9 | 7.71 × 10−38 | 3.2715 × 10−21 | 1.2 × 10−163 |
| SD | 4.7664 × 10−15 | 6.4396 × 10−21 | 1.1369 × 10−32 | 4.9436 × 10−76 | 5.1413 × 10−74 | 7.3985 × 10−25 | 7.00 × 10−21 | 4.6153 × 10−21 | 2.65 × 10−180 | |
| F2 | AV | 2.4794 | 0.3411 | 2.3702 × 10−8 | 7.1704 × 10−35 | 1.2952 × 10−34 | 0.5462 | 8.48 × 10−39 | 1.57 × 10−12 | 2.29 × 10−86 |
| SD | 2.2342 × 10−15 | 7.4476 × 10−17 | 5.1789 × 10−24 | 6.6936 × 10−50 | 1.9127 × 10−50 | 1.7377 × 10−16 | 5.92 × 10−41 | 1.42 × 10−12 | 1.05 × 10−99 | |
| F3 | AV | 1536.896 | 589.492 | 279.3439 | 2.7531 × 10−15 | 7.4091 × 10−15 | 1.7634 × 10−8 | 1.15 × 10−21 | 0.0864 | 5.83 × 10−70 |
| SD | 6.6095 × 10−13 | 7.1179 × 10−13 | 1.2075 × 10−13 | 2.6459 × 10−31 | 5.6446 × 10−30 | 1.0357 × 10−23 | 6.70 × 10−21 | 0.1444 | 4.06 × 10−77 | |
| F4 | AV | 2.0942 | 3.9634 | 3.2547 × 10−9 | 9.4199 × 10−15 | 1.2599 × 10−14 | 2.9009 × 10−5 | 1.33 × 10−23 | 2.6 × 10−8 | 1.91 × 10−70 |
| SD | 2.2342 × 10−15 | 1.9860 × 10−16 | 2.0346 × 10−24 | 2.1167 × 10−30 | 1.0583 × 10−29 | 1.2121 × 10−20 | 1.15 × 10−22 | 9.25 × 10−9 | 4.56 × 10−83 | |
| F5 | AV | 310.4273 | 50.26245 | 36.10695 | 146.4564 | 36.8607 | 41.7767 | 28.8615 | 46.049 | 28.4397 |
| SD | 2.0972 × 10−13 | 1.5888 × 10−14 | 3.0982 × 10−14 | 1.9065 × 10−14 | 2.6514 × 10−14 | 2.5421 × 10−24 | 4.76 × 10−3 | 0.4219 | 1.83 × 10−15 | |
| F6 | AV | 14.55 | 20.25 | 0 | 0.4435 | 0.6423 | 1.6085 × 10−9 | 7.10 × 10−21 | 0.398 | 0 |
| SD | 3.1776 × 10−15 | 1.2564 | 0 | 4.2203 × 10−16 | 6.2063 × 10−17 | 4.6240 × 10−25 | 1.12 × 10−25 | 0.1914 | 0 | |
| F7 | AV | 5.6799 × 10−3 | 0.1134 | 0.0206 | 0.0017 | 0.0008 | 0.0205 | 3.72 × 10−4 | 0.0018 | 2.75 × 10−5 |
| SD | 7.7579 × 10−19 | 4.3444 × 10−17 | 2.7152 × 10−18 | 3.87896 × 10−19 | 7.2730 × 10−20 | 1.5515 × 10−18 | 5.09 × 10−5 | 0.001 | 8.49 × 10−20 | |
| Genetic | PSO | GS | TLBO | GWO | WO | TS | MP | TSO | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F8 | AV | −8184.4142 | −6908.6558 | −2849.0724 | −7408.6107 | −5885.1172 | −1663.9782 | −5740.3388 | −3594.16321 | −12536.9 |
| SD | 833.2165 | 625.6248 | 264.3516 | 513.5784 | 467.5138 | 716.3492 | 41.5 | 811.3265 | 1.30 × 10−11 | |
| F9 | AV | 62.4114 | 57.0613 | 16.2675 | 10.2485 | 8.5265 × 10−15 | 4.2011 | 5.70 × 10−3 | 140.1238 | 0 |
| SD | 2.5421 × 10−14 | 6.3552 × 10−15 | 3.1776 × 10−15 | 5.5608 × 10−15 | 5.6446 × 10−30 | 4.3692 × 10−15 | 1.46 × 10−3 | 26.3124 | 0 | |
| F10 | AV | 3.2218 | 2.1546 | 3.5673 × 10−9 | 0.2757 | 1.7053 × 10−14 | 0.3293 | 9.80 × 10−14 | 9.6987 × 10−12 | 4.44 × 10−15 |
| SD | 5.1636 × 10−15 | 7.9441 × 10−16 | 3.6992 × 10−25 | 2.5641 × 10−15 | 2.7517 × 10−29 | 1.9860 × 10−16 | 4.51 × 10−12 | 6.1325 × 10−12 | 7.06 × 10−31 | |
| F11 | AV | 1.2302 | 0.0462 | 3.7375 | 0.6082 | 0.0037 | 0.1189 | 1.00 × 10−7 | 0 | 0 |
| SD | 8.4406 × 10−16 | 3.1031 × 10−18 | 2.7804 × 10−15 | 1.9860 × 10−16 | 1.2606 × 10−18 | 8.9991 × 10−17 | 7.46 × 10−7 | 0 | 0 | |
| F12 | AV | 0.047 | 0.4806 | 0.0362 | 0.0203 | 0.0372 | 1.7414 | 0.0368 | 0.0851 | 7.42 × 10−4 |
| SD | 4.6547 × 10−18 | 1.8619 × 10−16 | 6.2063 × 10−18 | 7.7579 × 10−19 | 4.3444 × 10−17 | 8.1347 × 10−12 | 1.5461 × 10−2 | 0.0052 | 1.75 × 10−18 | |
| F13 | AV | 1.2085 | 0.5084 | 0.002 | 0.3293 | 0.5763 | 0.3456 | 2.9575 | 0.4901 | 1.08 × 10−4 |
| SD | 3.2272 × 10−16 | 4.9650 × 10−17 | 4.2617 × 10−14 | 2.1101 × 10−16 | 2.4825 × 10−16 | 3.25391 × 10−12 | 1.5682 × 10−12 | 0.1932 | 3.41 × 10−17 | |
| Genetic | PSO | GS | TLBO | GWO | WO | TS | MP | TSO | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F14 | AV | 0.9986 | 2.1735 | 3.5913 | 2.2721 | 3.7408 | 0.998 | 1.9923 | 0.998 | 0.998 |
| SD | 1.5640 × 10−15 | 7.9441 × 10−16 | 7.9441 × 10−16 | 1.9860 × 10−16 | 6.4545 × 10−15 | 9.4336 × 10−16 | 2.6548 × 10−7 | 4.2735 × 10−16 | 8.69 × 10−16 | |
| F15 | AV | 5.3952 × 10−2 | 0.0535 | 0.0024 | 0.0033 | 0.0063 | 0.0049 | 0.0004 | 0.003 | 0.0003 |
| SD | 7.0791 × 10−18 | 3.8789 × 10−19 | 2.9092 × 10−19 | 1.2218 × 10−17 | 1.1636 × 10−18 | 3.4910 × 10−18 | 9.0125 × 10−4 | 4.0951 × 10−15 | 1.82 × 10−19 | |
| F16 | AV | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| SD | 7.9441 × 10−16 | 3.4755 × 10−16 | 5.9580 × 10−16 | 1.4398 × 10−15 | 3.9720 × 10−16 | 9.9301 × 10−16 | 2.6514 × 10−16 | 4.4652 × 10−16 | 8.65 × 10−17 | |
| F17 | AV | 0.4369 | 0.7854 | 0.3978 | 0.3978 | 0.3978 | 0.4047 | 0.3991 | 0.3979 | 0.3978 |
| SD | 4.9650 × 10−17 | 4.9650 × 10−17 | 9.9301 × 10−17 | 7.4476 × 10−17 | 8.6888 × 10−17 | 2.4825 × 10−17 | 2.1596 × 10−16 | 9.1235 × 10−15 | 9.93 × 10−17 | |
| F18 | AV | 4.3592 | 3 | 3 | 3.0009 | 3 | 3 | 3 | 3 | 3 |
| SD | 5.9580 × 10−16 | 3.6741 × 10−15 | 6.9511 × 10−16 | 1.5888 × 10−15 | 2.0853 × 10−15 | 5.6984 × 10−15 | 2.6528 × 10−15 | 1.9584 × 10−15 | 4.97 × 10−16 | |
| F19 | AV | −3.85434 | −3.8627 | −3.8627 | −3.8609 | −3.8621 | −3.8627 | −3.8066 | −3.8627 | −3.8627 |
| SD | 9.9301 × 10−17 | 8.9371 × 10−15 | 8.3413 × 10−15 | 7.3483 × 10−15 | 2.4825 × 10−15 | 3.1916 × 10−15 | 2.6357 × 10−15 | 4.2428 × 10−15 | 6.95 × 10−16 | |
| F20 | AV | −2.8239 | −3.2619 | −3.0396 | −3.2014 | −3.2523 | −3.2424 | −3.3206 | −3.3211 | −3.3219 |
| SD | 3.97205 × 10−16 | 2.9790 × 10−16 | 2.1846 × 10−14 | 1.7874 × 10−15 | 2.1846 × 10−15 | 7.9441 × 10−16 | 5.6918 × 10−15 | 1.1421 × 10−11 | 1.89 × 10−15 | |
| F21 | AV | −4.3040 | −5.3891 | −5.1486 | −9.1746 | −9.6452 | −7.4016 | −5.5021 | −10.1532 | −10.1532 |
| SD | 1.5888 × 10−15 | 1.4895 × 10−15 | 2.9790 × 10−16 | 8.5399 × 10−15 | 6.5538 × 10−15 | 2.3819 × 10−11 | 5.4615 × 10−13 | 2.5361 × 10−11 | 5.96 × 10−16 | |
| F22 | AV | −5.1174 | −7.6323 | −9.0239 | −10.0389 | −10.4025 | −8.8165 | −5.0625 | −10.4029 | −10.4029 |
| SD | 1.2909 × 10−15 | 1.5888 × 10−15 | 1.6484 × 10−12 | 1.5292 × 10−14 | 1.9860 × 10−15 | 6.7524 × 10−15 | 8.4637 × 10−14 | 2.8154 × 10−11 | 1.79 × 10−15 | |
| F23 | AV | −6.5621 | −6.1648 | −8.9045 | −9.2905 | −10.1302 | −10.0003 | −10.3613 | −10.5364 | −10.5364 |
| SD | 3.8727 × 10−15 | 2.7804 × 10−15 | 7.1497 × 10−14 | 1.1916 × 10−15 | 4.5678 × 10−15 | 9.1357 × 10−15 | 7.6492 × 10−12 | 3.9861 × 10−11 | 9.33 × 10−16 | |
| Function | TSO | MP | TS | WO | GWO | TLBO | GS | PSO | Genetic | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Unimodal (F1–F7) | Friedman value | 7 | 37 | 16 | 42 | 27 | 28 | 37 | 56 | 57 |
| Friedman rank | 1 | 5 | 2 | 6 | 3 | 4 | 5 | 7 | 8 | ||
| 2 | High-dimension multimodal (F8–F13) | Friedman value | 6 | 33 | 27 | 38 | 24 | 25 | 32 | 37 | 40 |
| Friedman rank | 1 | 6 | 4 | 8 | 2 | 3 | 5 | 7 | 9 | ||
| 3 | Fixed-dimension multimodal (F14–F23) | Friedman value | 10 | 15 | 33 | 33 | 31 | 35 | 38 | 45 | 55 |
| Friedman rank | 1 | 2 | 4 | 4 | 3 | 5 | 6 | 7 | 8 | ||
| 4 | All 23 functions | Friedman value | 23 | 85 | 76 | 113 | 82 | 88 | 107 | 138 | 152 |
| Friedman rank | 1 | 4 | 2 | 7 | 3 | 5 | 6 | 8 | 9 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doumari, S.A.; Givi, H.; Dehghani, M.; Montazeri, Z.; Leiva, V.; Guerrero, J.M. A New Two-Stage Algorithm for Solving Optimization Problems. Entropy 2021, 23, 491. https://doi.org/10.3390/e23040491
Doumari SA, Givi H, Dehghani M, Montazeri Z, Leiva V, Guerrero JM. A New Two-Stage Algorithm for Solving Optimization Problems. Entropy. 2021; 23(4):491. https://doi.org/10.3390/e23040491
Chicago/Turabian StyleDoumari, Sajjad Amiri, Hadi Givi, Mohammad Dehghani, Zeinab Montazeri, Victor Leiva, and Josep M. Guerrero. 2021. "A New Two-Stage Algorithm for Solving Optimization Problems" Entropy 23, no. 4: 491. https://doi.org/10.3390/e23040491
APA StyleDoumari, S. A., Givi, H., Dehghani, M., Montazeri, Z., Leiva, V., & Guerrero, J. M. (2021). A New Two-Stage Algorithm for Solving Optimization Problems. Entropy, 23(4), 491. https://doi.org/10.3390/e23040491








